伪随机码

LFSR

在数字通信中，一般使用伪随机序列（Pseudo-Noise，PN）作为训练序列。PN 序列的特点是，尽管其序列产生器有确定的构造方法，但 PN 序列本身具有很多类似随机序列的性质。

最常见的二进制 PN 序列是最大长度线性反馈移位寄存器（Linear-Feedback Shift Register，LFSR）序列，简称 m 序列，它是由一个线性反馈的 $n$ 级移位寄存器生成的。所谓线性反馈，是指反馈函数中仅包含模 2 加运算而不含非线性运算。

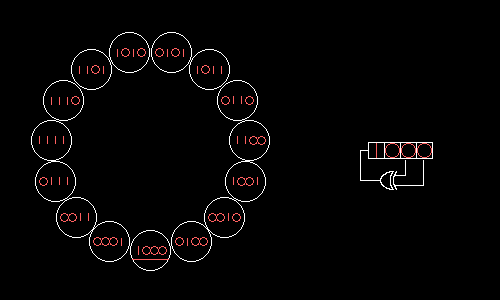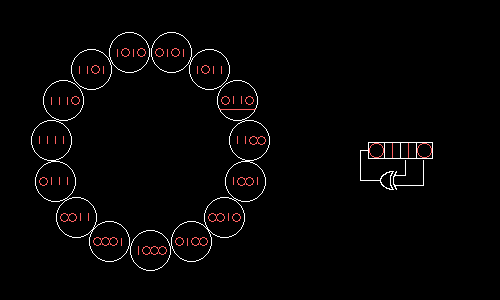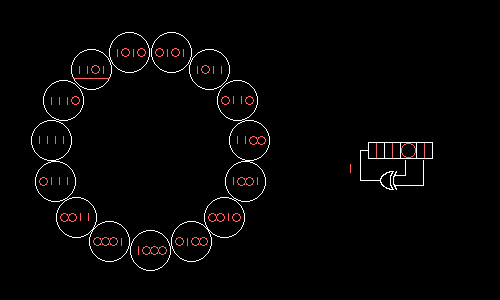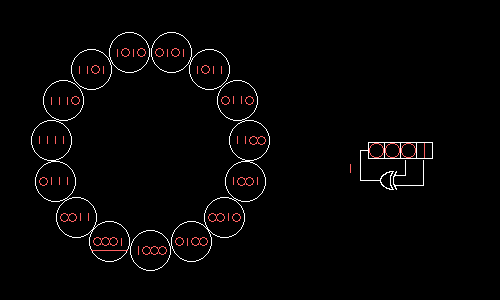
上图中该 LFSR 对应的生成多项式为：$$1+x^3+x^4$$

PN 序列的主要用途是改变信号的特性，用于加密或者扩频，广泛应用于数字通信中。

判断一个序列是否是PN序列，也就是伪随机序列的判据很明确：

• { 0 、 1 } {0、1} {0、1} 的个数接近相等
• 连续 0 或 1 的子序列比例确定
• 自相关函数类似白噪声

m-序列

m 序列是有 $n$ 级线性移位寄存器产生的周期为 $2^n-1$ 的码序列，是最长线性移位寄存器序列的简称。码分多址系统主要采用两种长度的 m 序列：一种是周期为 $2^{15}-1$ 的 m 序列，又称短 PN 序列；另一种是周期为 $2^{42}-1$ 的 m 序列，又称为长 PN 码序列。m 序列主要有两个功能：

• 扩展调制信号的带宽到更大的传输带宽，即所谓的扩展频谱。
• 区分通过多址接入方式使用同一传输频带的不同用户的信号。

原理

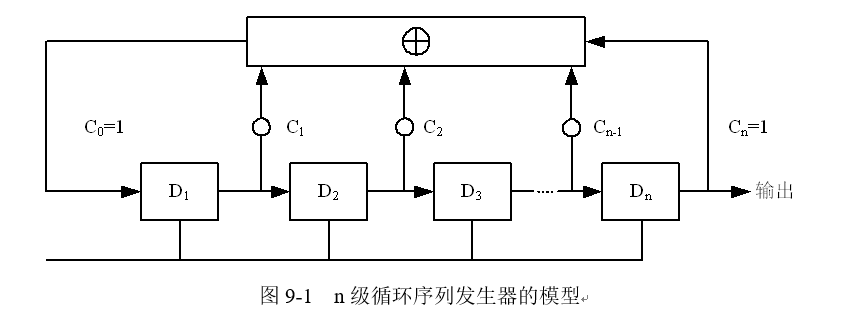
如下图所示是由 $n$ 级移位寄存器构成的码序列发生器。寄存器的状态取决于时钟控制下输入的信息（0 或 1），例如第 $i$ 级移位寄存器状态决定于前一时钟脉冲后的第 $i－1$ 级移位寄存器的状态。图中 $C_0,C_1,\cdots ,C_n$ 均为反馈线，其中 $C_0＝C_n＝1$ 表示反馈连接。因为 m 序列是由循环序列发生器产生的，因此 $C_0$ 和 $C_n$ 肯定为 1，即参与反馈。而反馈系数 $C_1,C_2,\cdots ,C_{n－1}$ 若为 1，参与反馈；若为 0，则表示无反馈连线。

假设每一级反馈从左到右输出依次为 $a_n,a_{n-1},\cdots ,a_1,a_0$，输出端为 $a_0$，则总的模二加的结果是$a_n$：
$$a_n=C_1{a}_{n-1}\oplus C_2{a}_{n-2}v\cdots \oplus C_n{a}_0$$
将 $C_0{a}_n$ 移到右边为
$$F=C_0{a}_n\oplus C_1{a}_{n-1}\oplus C_2{a}_{n-2}v\cdots \oplus C_n{a}_0=\sum _{i=0}^n\oplus C_i{a}_{n-i}=0$$
换成代数式
$$f(x)=\sum _{i=0}^n{C}_i{x}^i$$

一个线性反馈移动寄存器能否产生 m 序列，决定于它的反馈系数。例如一个 LFSR 对应的生成多项式为：$$1+x^3+x^4$$
这个代数式就表示 $C_0=C_3=C_4=1$。

每一次移位都会使移位寄存器切换到下一个状态，4 位移位寄存器总共可以有 $2^4=16$ 种状态，除去 $0000$ 状态之外，该 LFSR 可以在剩下的 15 个状态中循环切换。

如果我们令 LFSR 的状态从0001开始，每一次移位都将 $x^4$ 输出，则可以生成的随机码序列为：

$$1-0-0-0-1-0-0-1-1-0-1-0-1-1-1\dots \dots$$

完成15个 bit 输出后，循环重复。

那么为什么选用第 3 位相加反馈？如果是选用第 2 位会怎么样？同样以 0001 开始，LFSR 的状态切换过程为：

可以看到，只遍历了 6 个状态就回到了初始状态，生成的随机序列为 $$1-0-0-0-1-0\dots \dots$$

只有 6 个随机码，然后开始循环重复，随机性显然不如之前的多项式。前面的生成多项式 $1+x^3+x^4$ 称为 MLS（Maximum Length Sequence），常用的 PRBS 都是 MLS。

仿真

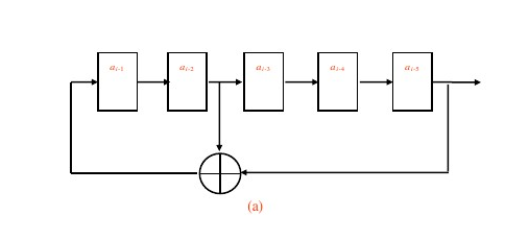
The PN-sequences are generated from a 5-stage linear feedback shift registers (LFSR), where the feedbacks from the registers are taken in such a way that it results in maximum length sequences (e.g. by taking the feedbacks from second and fifth stages).

解答：$f(x)=1+x^2+x^5$

5 级 LFSR 为 $[C_0,C_1,C_2,C_3,C_4,C_5]=[101001]$

%***************************************************
% 此函数用来生成m序列
% coef为反馈系数向量
%***************************************************
coef = [0 1 0 0 1]; %[c0=1]不写 c1 c2 c3 c4 c5

m=length(coef);
len=2^m-1; % 得到最终生成的m序列的长度     
backQ=0; % 对应寄存器运算后的值，放在第一个寄存器
seq=zeros(1,len); % 给生成的m序列预分配
registers = [zeros(1, m-1) 1]; % 给寄存器分配初始结果

code = [];

for i=1:len
    %disp(i);
    code = [code registers(m)];
    %disp(registers);
    seq(i)=registers(m);
    backQ = mod(sum(coef.*registers), 2); %特定寄存器的值进行异或运算，即相加后模2
    registers(2:length(registers)) = registers(1:length(registers)-1); % 移位
    registers(1)=backQ; % 把异或的值放在第一个寄存器的位置
end

disp(code);

相关系数

在扩频系统中，我们比较关心伪随机码的相关特性，下面就介绍这些特性：
设有两条长为 $n$ 的序列 { a } {a} {a} 和 { b } {b} {b}，序列中的元素分别为 $a_i,b_i$。

通过自相关函数考量伪随机码的自相关特性，自相关函数的定义：
$$R(j)=\sum _{i=0}^{n-1}{a}_j{a}_{i+j}$$
自相关系数为
$$\rho (j)=\frac{1}{n}\sum _{i=0}^{n-1}{a}_j{a}_{i+j}$$

以 $n=4$ 为例，则有

x = -1*len:1:len;

for i = 1:2*len+1
    j = x(i);
    % 循环移位
    code_j = circshift(code', j)';
    R(i) = sum(code.*code_j)/len;
end

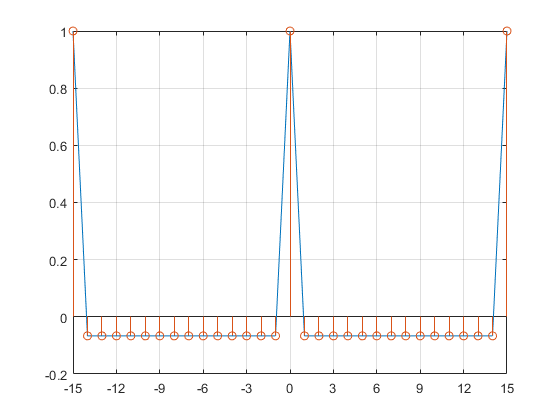
可知
$$\rho (j)=\{\begin{array}{rlr}1& ,& j=0,\\ -\frac{1}{n}& ,& j\ne 0.\end{array}$$

最后

以上就是听话小懒虫为你收集整理的对伪随机码的梳理伪随机码的全部内容，希望文章能够帮你解决对伪随机码的梳理伪随机码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。