第六章 - UVA816 - Abbott's Revenge - bfs

69 阅读 0 评论 46 点赞

我是靠谱客的博主还单身纸飞机，最近开发中收集的这篇文章主要介绍第六章 - UVA816 - Abbott's Revenge - bfs，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目链接

题目意思：

求从起点到重点的一条最短路。

输入：

SAMPLE //地图名字，若为"END"则结束

3 1 N 3 3 //起点位置，面朝方向，终点位置

1 1 WL NR * //地图的描述，以*结尾，意思是，在点（1,1）时，若面朝W，只能左转，若面朝N，则只能右转

1 2 WLF NR ER *

1 3 NL ER *

2 1 SL WR NF *

2 2 SL WF ELF *

2 3 SFR EL *

0 //结束输入

分析：

1、设node，存点的坐标及朝向

2、设入口位置为(r0,c0)朝向为dir，则初始状态是入口位置朝dir走一步的状态(r1,c1,dir)

3、d[r][c][dir]表示初始状态到(r,c,dir)的最短路径长度，并用p[r][c][dir]保存了状态(r,c,dir)在dfs树中的父节点。

4、has_edge[r][c][dir][turn]表示当前状态是(r,c,dir)是否可以沿着转弯方向turn行走

注意：这个地图是自己画出的，不是一个长方形啦。

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<queue>
#include<algorithm>

using namespace std;

struct node{
	int r,c,dir;
	node(int r=0,int c=0,int dir=0):r(r),c(c),dir(dir) {}
};
const int maxn=10;
const char* dirs="NESW";//四个方向 
const char* turns="FLR";//三个转向，左转，右转，直行 
const int dr[]={-1,0,1,0};
const int dc[]={0,1,0,-1};

int d[maxn][maxn][4],has_edge[maxn][maxn][4][3];
int c1,r1,r2,c2,dir,r0,c0;
node p[maxn][maxn][4];
string name;

int dir_id(char c){//把方向转化成数字，eg,N=>0
	return strchr(dirs,c)-dirs;
}
int turn_id(char c){//把转向转化成数字，eg,F=>0 
	return strchr(turns,c)-turns;
}

node walk(const node &u, int turn){
    //行走函数，根据当前的状态u和转弯状态计算出后继状态 
    int dir = u.dir;
    if (turn == 1) dir = (dir + 3) % 4;//左转 
    if (turn == 2) dir = (dir + 1) % 4;//右转
    //直行方向不变 
    return node(u.r + dr[dir], u.c + dc[dir], dir);
}


void print_ans(node u){
	vector<node> nodes;
	for(;;){
		nodes.push_back(u);
		if(d[u.r][u.c][u.dir]==0)break;
		u=p[u.r][u.c][u.dir];
	}
	nodes.push_back(node(r0,c0,dir));
	int cnt=0;
	
	for(int i=nodes.size()-1;i>=0;i--){
        //每行前有两个空格，坐标之间有一个 
		if(cnt%10==0)printf(" ");
		printf(" (%d,%d)",nodes[i].r,nodes[i].c);
		if(++cnt%10==0)printf("n");
	}
	if(nodes.size()%10!=0)printf("n");
}
bool inside(int r,int c){//地图的长宽均不超过9不小于1
	return r>=1&&r<=9&&c>=1&&c<=9;
}
void solve(){
	queue<node> q;
	memset(d,-1,sizeof(d));
	node u(r1,c1,dir);
	d[u.r][u.c][u.dir]=0;
	q.push(u);
	while(!q.empty()){
		node u=q.front();q.pop();
		if(u.r==r2&&u.c==c2){
			print_ans(u);
			return ;
		}
		for(int i=0;i<3;i++){//3种转弯方式 
			node v=walk(u,i);//v是u向i方向走一格得到的状态
            //u能向i方向转&&v点在图中&&没走过这个点 
			if(has_edge[u.r][u.c][u.dir][i]&&inside(v.r,v.c)&&d[v.r][v.c][v.dir]<0){
				d[v.r][v.c][v.dir] = d[u.r][u.c][u.dir] + 1;
                p[v.r][v.c][v.dir] = u;
                q.push(v);
			}
		}
	}
	printf("  No Solution Possiblen");
}


bool scan(){
    memset(has_edge,0,sizeof(has_edge));
	cin>>name;
	if(name=="END")return false;
	char s[100];
	cin>>r0>>c0>>s>>r2>>c2;
	cout<<name<<endl;
    //初始位置就是起点朝面朝的方向走一步 
	r1=r0+dr[dir_id(s[0])];
	c1=c0+dc[dir_id(s[0])];
	
	dir=dir_id(s[0]);
	int r,c;
	while(cin>>r){
		if(r==0)break;
		cin>>c;
		char s2[100];
		while(cin>>s2){
			if(s2[0]=='*')break;
			int l=strlen(s2);
			for(int i=1;i<l;i++){//构造地图：把坐标为(r,c)朝向为s2[0],对应的转向全设为1，表示可向这转 
				has_edge[r][c][dir_id(s2[0])][turn_id(s2[i])]=1;
			}
		}
	}
	return true;
}
int main(){
	while(scan()){
		solve();
	}
	return 0;
}

注意：

1、strchr函数：

函数原型：extern char *strchr(char *str,char character)

参数说明：str为一个字符串的指针，character为一个待查找字符。
所在库名：#include <string.h>
函数功能：从字符串str中寻找字符character第一次出现的位置。
返回说明：返回指向第一次出现字符character位置的指针，如果没找到则返回NULL。

举例：

#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;

int main(){
	char* s="abcdefg";
	char c='e';
	char* p=strchr(s,c);
	cout<<p<<endl;
	cout<<strchr(s,c)<<endl;
	cout<<strchr(s,c)-s<<endl;
}

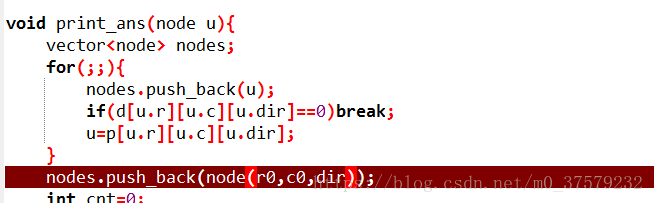
2、红色圈出部分的作用

相当于构造函数

若删去，会报错，如下：

错误1

错误2

错误3

除了上述代码那样写，还可以：

（删去构造函数的情况下）

显示定义一个结构体，把值赋进去

node walk(const node &u, int turn){
    int dir = u.dir;
    if (turn == 1) dir = (dir + 3) % 4;//左转 
    if (turn == 2) dir = (dir + 1) % 4;//右转
	//直行方向不变 
	struct node temp{u.r + dr[dir], u.c + dc[dir], dir};
    return temp;
}

或者

加个大括号

node walk(const node &u, int turn){
    int dir = u.dir;
    if (turn == 1) dir = (dir + 3) % 4;//左转 
    if (turn == 2) dir = (dir + 1) % 4;//右转
	//直行方向不变 
	return node{u.r + dr[dir], u.c + dc[dir], dir};
}