信息与系统_信号与系统的描述

一、信号的分类

1、一维信号和多维信号
• 如果某函数只依赖于单个变量，则称该信号为 一维信号，习惯用函数f(t)来表示一个以时间t 为自变量的实值函数或标量函数。称t为自变量， 称f(t)为因变量。
• 如果某函数依赖于两个或多个变量，则称该信号为多维信号。一个二维信号，我们可以用 f(x,y)表示

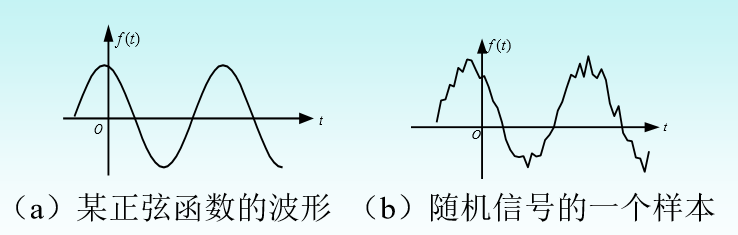
2、确定信号和随机信号
• 确定信号是指能够以确定的时间函数表示的信 号，其在任意时刻都有确定的函数值。
• 随机信号也称为不确定信号，不是时间的确定 函数，具有不可预知性。随机信号不能用数学 函数来准确地描述，一般是描述它的统计特性

3、连续时间信号和离散时间信号
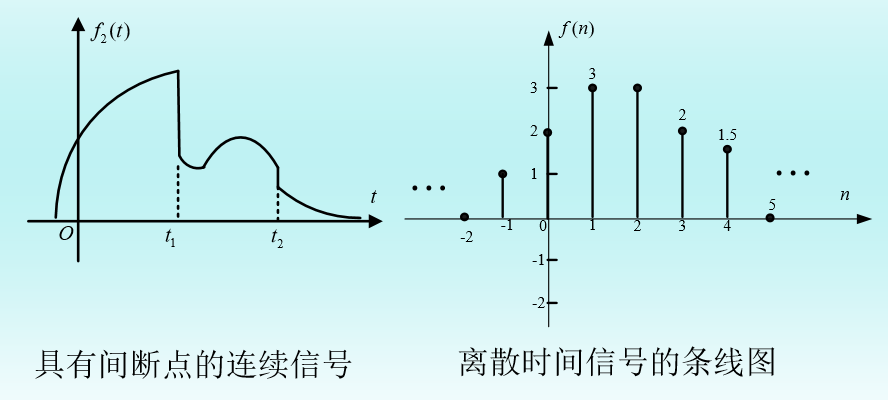
•连续时间信号是指如果在某个时间区间内，对 于一切时间值，除有限个间断点外，函数都能 给出确定的函数值。
• 离散时间信号只在某些离散的时间点才有定义， 即信号的自变量只取离散的数值，这些点之间 的值是不被定义的。

4、周期信号和非周期信号
• 周期信号是指一个连续时间函数对所有的满足：f（t）=f（t+kT） , k=…-1,0,1,2
• 周期T的倒数称为周期信号的基本频率 f=1/T
• 频率f的量纲是赫兹（Hz），一个完整循环对 应于2π弧度，定义角频率ω如下， 单位为：rad/s w=2πf=2π/T
5、周期的判断
• 试判断下列信号是否为周期信号。若是，确定 其周期。
(1) f1(t)=sin 2t+cos 3t
(2) f2(t)=cos 2t+sinπt
解：如果两个周期信号x(t)和y(t)的周期的比为有理数，则它们的和信号f(t)=x(t)+y(t)是一个 周期信号，其周期是x(t)和y(t)周期的最小公倍数；若周期的比为无理数，则和信号周期不存在。

二、常见的工程信号

1、正弦信号
• 正弦信号和余弦信号仅在相位上相差π/2，常统 称为正弦信号，其典型的数学表达式为：

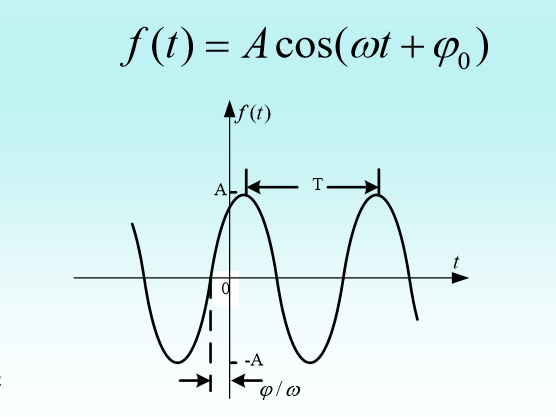
2、指数信号

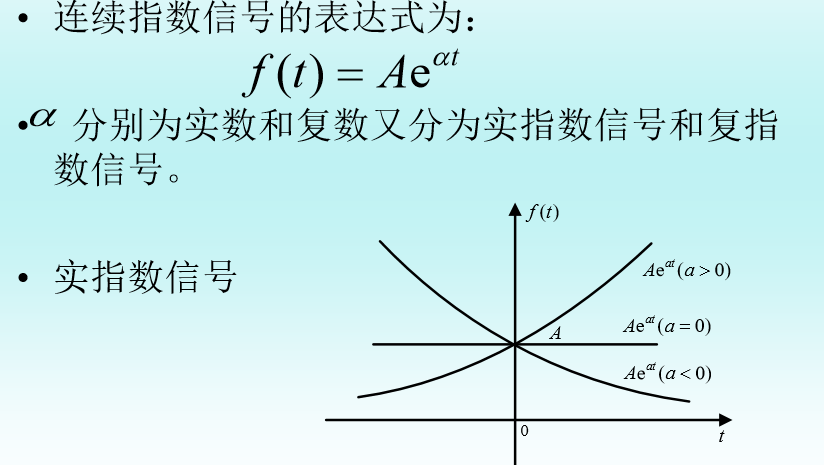
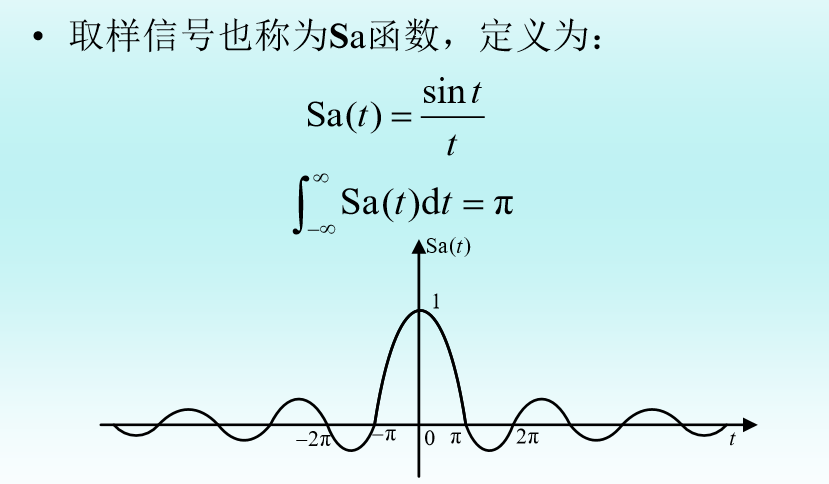
3、取样信号

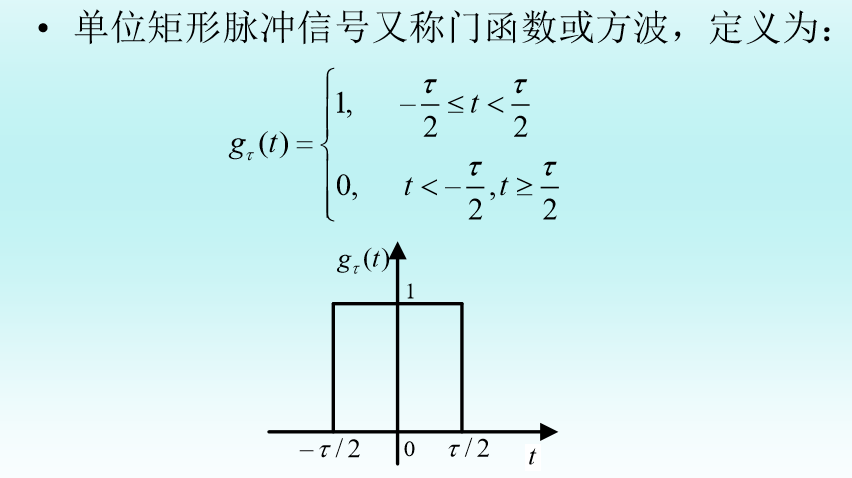
4、单位矩形脉冲信号

5、符号函数

三、信号的基本运算

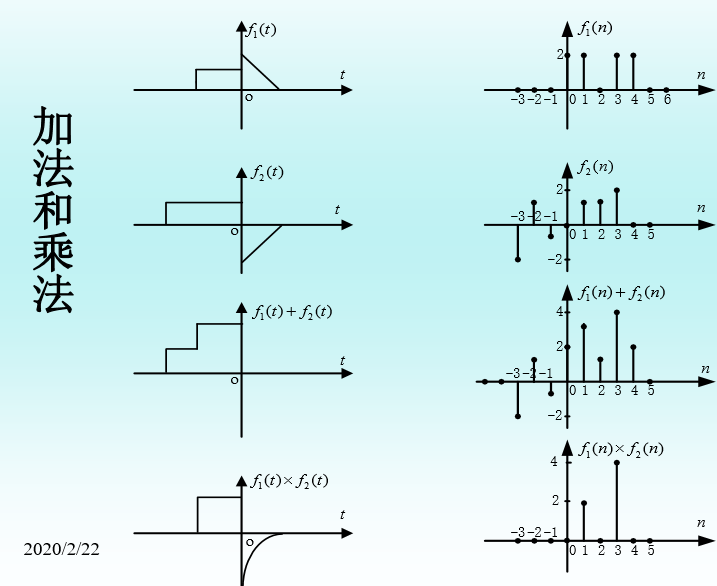
1、加法和乘法
•两个信号相加，其和信号在任意时刻的信号值等于两信号在该时刻的信号值之和。两个信号相乘，其积信号在任意时刻的信号值等于两信号在该时刻的信号乘积。
即：s（t）=f1（t）+ f2（t）
P（t）= f1（t）* f2（t）。

2、微分与积分
略，如像具体了解，可以私聊或评论

3、位移（时移/平移）
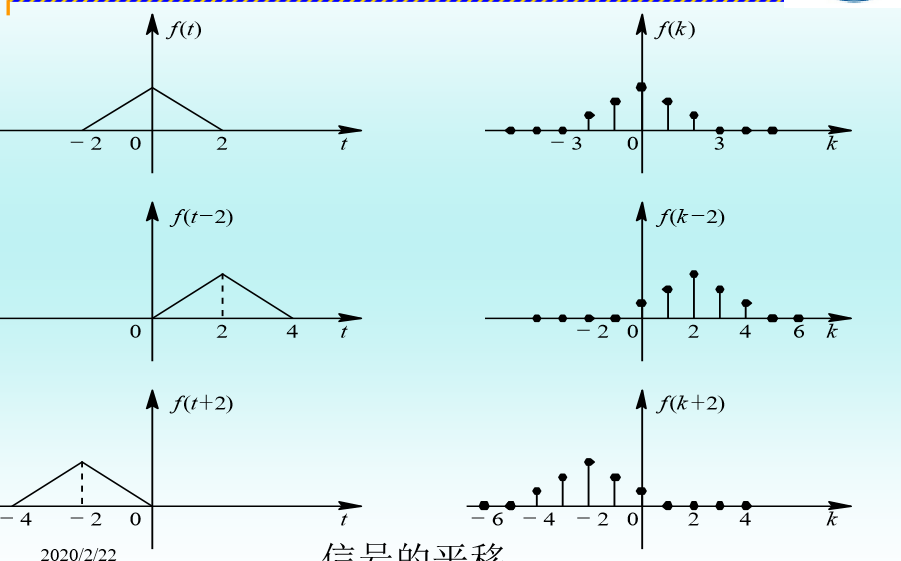
• 信号f(t)经过加工后输出的波形形状没有发生改 变,只是延迟（或提前）了t0时间单位 ,表达式变 为f(t-t0)(或f(t+t0))。
• 做平移时，是将f(t)的波形沿着时间t轴向右 （或左）水平移动了t0个时间单位。
（）
4、反折（或翻转）
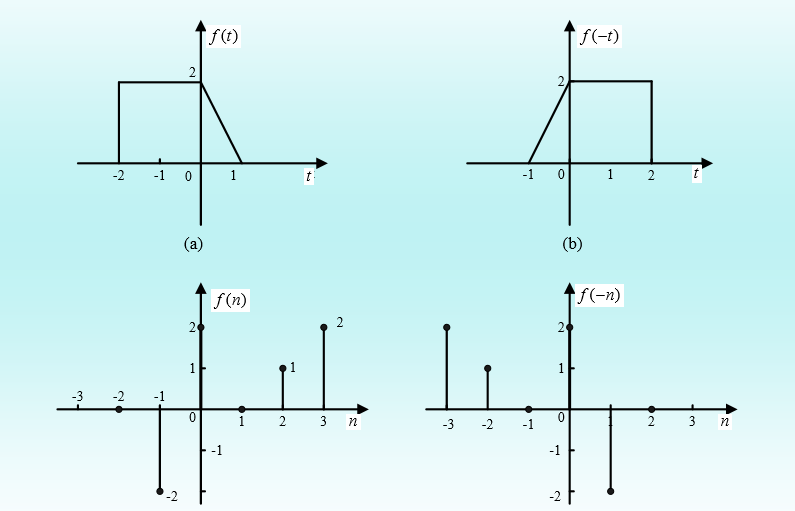
• 将信号f(t)(或f(n))的自变量t(或k)换成-t(或-n)， 得到另一个信号f(-t)(或f(-n))， 称这种变换为信 号的反折 。

• 做反折运算，可将f(t)或f(n)的波形绕纵坐标轴 翻转180°， 即为f(-t)或f(-n)的波形

5、尺度变换
y(t)=f(at)
• 若a>1，对信号进行尺度变换是将原信号沿着 横轴方向压缩；若0<a<1，对信号进行尺度变 换是将原信号沿着横轴方向展宽。
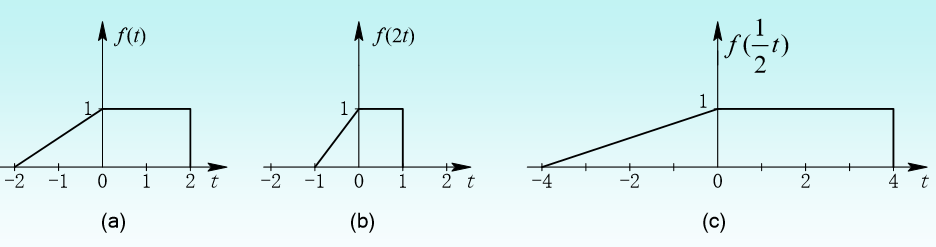注意：这里的一切操作都是对t进行操作，而不是多f（）里面的整体内容！！！！
6、平移、反折、尺度变换后的验证
• 因为映射函数不变，故必须使变换后的函数和 变换前的函数当自变量取等值时，函数值也是 相同的。

四、阶跃信号与冲激响应

1、单位阶跃信号u(t)的定义为：

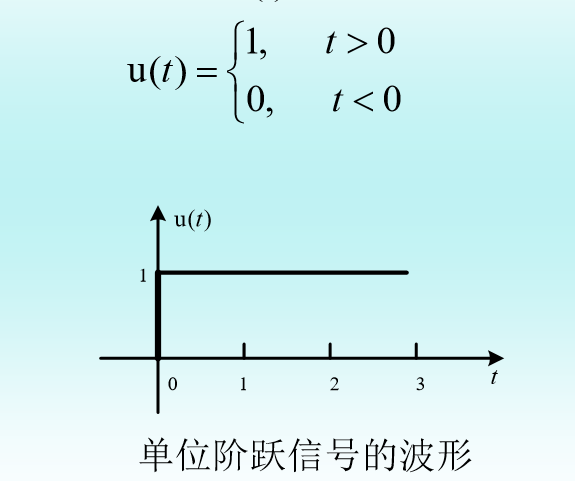
2、单位冲激响应
• 单位冲激信号 δ(t)的一种定义是：

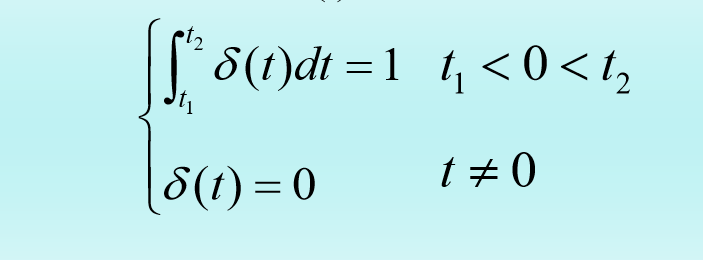
• 定义表明δ函数除原点以外，处处为零，但其 面积为1。
3、阶跃信号与冲激信号的关系


4、单位冲激信号的性质-采样特性

5、冲激偶信号与普通函数相乘

6、尺度变换

7、奇偶特性

五、系统的特性及分类

1、线性系统
• 如果任意两个激励共同作用时，系统的响应等 于每个激励单独作用时所产生的响应之和，就 称系统具有叠加性或可加性，可表示为：

.
2、时不变系统
• 参数不随时间变化的系统，称为时不变系统或 定常系统，否则称为时变系统。 • 一个时不变系统，其内部参数不随时间变化， 所以系统的关系也不会随时间变化。 即输入信号无论什么时间接入系统，系统的输 出都是相同的（只可能有相应的延时），可表 示为： f()→yf()
3、因果特性
• 一个系统，如果激励在t<t0(或n<n0)时为零，相 应的零状态响应在t<t0(或n<n0)时也恒为零，就 称该系统具有因果性，并称这样的系统为因果 系统；否则，为非因果系统。
• 因此，在因果系统里，不可能在输入加入系统 前而获得输出 。
4、稳定性

最后

以上就是细腻毛衣为你收集整理的信息与系统_信号与系统的描述的全部内容，希望文章能够帮你解决信息与系统_信号与系统的描述所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。