【数字信号处理】关于实现FIR滤波器的一些问题

在知乎上看到了一个提问，稍微整理了一下关于这些问题的回答https://www.zhihu.com/question/29945169

FIR其实就是下面这个公式，其中数组x[]为输入，数组h[]为滤波参数（已知），数组y[]为滤波输出：

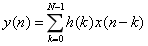
问题1

“实现FIR滤波过程就是上面这个过程？这么简单？还是自己理解错了根本不是这么回事？（想确认：对于实现这块，上面的理解对不对）”

从理论上，FIR就是上面这个过程，但是做成实际使用的系统会遇到各种问题阻止你实现这个公式。

情况1：已知FIR滤波器在时域的序列

这可能是最容易使用这个公式的情况了。但是可以看到，这个公式的复杂度是O(n^2)的，如果你的FIR序列过长，将会导致严重的效率问题。一般我们会学习FFT来提高效率。学习FFT就需要学习频域。

同时，一般情况下，你的x会非常非常长。比如一首60s的歌曲，采样率在44.1kHz，你将有一个长达44100*60 = 2646000的序列。你真的打算把这么长的序列存到内存里，然后直接用上面的公式吗?我们会学习overlap add和overlap save来解决这个问题。

更多时候，我们关心的是平稳信号的属性（见stationarity)，这是我们要用到短时傅立叶变换(STFT)。这里涉及到了很多的窗函数的知识。

**平稳信号的属性：**平稳过程（或严格/严格平稳过程或强/强烈平稳过程）是随机过程，其随时间推移的无条件联合概率分布不会改变。因此，诸如均值和方差之类的参数也不会随时间变化。

傅立叶变换(FT)：
FT在平稳信号的分析和处理中有着突出贡献的原因在于，人们利用它可以把复杂的时间信号和空间信号变换到频率域中，然后用相对简单的频谱特性去分析和发现原信号的动态特性。

FT 正变换告诉我们：从时间（空间）信号中提取信号的频谱信息F(W)，就是使用整个时间域的所有信息来计算单个确定频率的谱值（频域函数F(w)的任一频率w0对应的函数值），这是由时间轴（ − ∞ , ∞ ）上的确定信号f(t)决定的。因此，它求出的频域函数对应的时整个时间轴，所以可以知道，傅里叶变换对频谱的描绘是“全局性”的，不能反映时间维度局部区域上的特征,人们虽然从傅立叶变换能清楚地看到一整段信号包含的每一个频率的分量值，但很难看出对应于频率域成分的不同时间信号的持续时间和发射的持续时间，缺少时间信息使得傅立叶分析再更精密的分析中失去作用。

短时傅立叶变换(STFT)：

基本思想：局部平稳化
把长的非平稳随机过程看成是一系列短时随机平稳信号的叠加，短时性可通过在时间上加窗口函数实现（即截取一部分源数据）。通过该方法，人们至少可以说，无论发现了什么频率成分，它一定是发生在信号被截取的某个特定时间段内。

具体实现则是通过在傅立叶变换中，使用时间窗口函数g(t−u)与源信号f(t)相乘，实现在u附近的加窗口和平移，然后进行傅立叶变换。在线性空间有一个可测的、平方可积的函数，对其进行短时傅立叶变换：

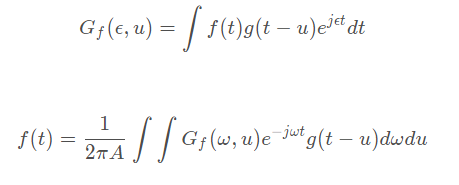
由短时傅立叶变换对函数（信号）进行的分析，相当于用一个形状、大小和放大倍数相同的“放大镜”在时－频域平面上移动去观察某固定长度时间内的频率特性。这里的问题是：尽管窗式傅立叶变换能解决变换函数的时域局域化问题，但是，其窗口的大小和形状是固定的，即窗口没有自适应性。这意味着什么？不能针对具体的问题进行优化。

而实际问题中，则各个要求“私人定制”，对于信息集中在高频的信号，由于波形相对较窄，时间间隔要小，采样频率要高，以求给出比较好的精度，进而更好地确定峰值，或者说需要用窄的时域窗来反映信息的高频成分；而对于低频谱信息，由于波形相对是宽的，时间段要相对的长才能给出完整的信号信息，或者说必须用较宽的时域窗来反映信息的低频成分。
这样，真正合适的做法是“放大镜”的长宽是可以变化的，正是为了实现这样的目的，人们引进了小波变换

短时傅里叶变换是最常用的一种时频分析方法，它通过时间窗内的一段信号来表示某一时刻的信号特征。在短时傅里叶变换过程中，窗的长度决定频谱图的时间分辨率和频率分辨率，窗长越长，截取的信号越长，信号越长，傅里叶变换后频率分辨率越高，时间分辨率越差；相反，窗长越短，截取的信号就越短，频率分辨率越差，时间分辨率越好，也就是说短时傅里叶变换中，时间分辨率和频率分辨率之间两者不可兼得，必须根据具体需求进行取舍。

简单来说，短时傅里叶变换就是先把一个函数和窗函数进行相乘，然后再进行一维的傅里叶变换。并通过窗函数的滑动得到一系列的频谱函数，将这些结果依次开便得到一个二维的时频图。

短时傅里叶变换的公式为

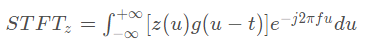
其中Z(u)为源信号，g(u-t )为窗函数。

情况 2 ：你知道自己要设计一个什么样频率响应的滤波器（比如低通滤波器)

知道低通滤波器的频域响应，要转化为时域响应，只能得到IlR，此时的响应是无限长的。有限长信号通过IR滤波，会得到无限长信号，很不实用。这时我们要用有限长响应去逼近无限长响应，会用到零极点图，窗函数法，多采样率滤波器等方法去实现。

问题2

不同的滤波类型(高通、低通、带通、带阻滤波）主要表现滤波参数h的不同?

高通/低通的不同，更多表现在频域上的不同。在时域上不易看出什么不同。

问题3

如果真这么简单为什么教材不写简单一点，非得要扯那些复数域、z变换？这是什么心态？纯粹让外行看不懂吗？

数字信号处理涉及到的问题多种多样，要解决的工程问题也很繁杂。所以教材里包罗万象也就不奇怪了。FIR滤波器只是数字信号处理的一部分，要学好FIR滤波器，需要比较完备的知识储备。如果真正想要解决实际问题的话，建议还是一步一步从经典教材的第一章看起。如果只是想用FIR做一些简单的算法验证，在知道FIR滤波器时域响应的情况下，用这个公式也是可以实现的。

问题4

难道是说设计一个滤波器很难（需要用到那么多概念），实现滤波器就是我上面理解的那个公式？

设计一个滤波器，要考虑到对这个滤波器的实际要求。设计的时候，一般会对FIR长度，频响有要求。如果是一个过渡带很宽的低通滤波器，用比较低的阶数就能设计出来;如果过渡带很窄，则需要更高级的设计方法。
总之，实现FIR滤波器，在应用场景极其简单的情况，可以用上面的公式。你是码农，应该了解随便写个玩具程序和真正可以用的工程中间差了多少吧?
推荐玩一玩一个滤波器设计工具，Matlab里的fdatool。简单好用/即时上手。可能会对你理解FIR滤波器有帮助。

FIR滤波器结构就是这么简单，因为结构简单，只用了乘法加法，计算时间确定，没有迭代之类的过程，很适合计算机计算，所以才应用这么广泛。虽然结构简单，但是参数选择是有讲究的。原始信号结构怎么样，噪声有什么特点，都是选择滤波器参数的重要考虑因素。经典理论中，噪声都是有一定规律的，这个规律就是频率，所以一般会从频域、复数域入手考虑。为了在频域考虑问题，需要把通常情况下采集到的时间序列转换为频谱，这就涉及到z变换了

最后

以上就是明亮短靴为你收集整理的【数字信号处理】关于实现FIR滤波器的一些问题的全部内容，希望文章能够帮你解决【数字信号处理】关于实现FIR滤波器的一些问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。