数字图像处理习题（连通分量的标记）

98 阅读 0 评论 65 点赞

我是靠谱客的博主欢喜天空，最近开发中收集的这篇文章主要介绍数字图像处理习题（连通分量的标记），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

连通成分的标记原理

连通成分是给二值图像中的每个连通区域标上一个特定标号的算法，该算法可以用来对图像中的目标进行定位和计数。
邻域：
中间像素与他周围像素之间的位置关系决定了是几邻域连接，如下图表示了4邻域与8邻域
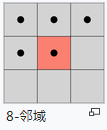
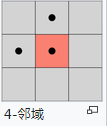
在这里插入图片描述

算法思路

使用的数据结构为队列，用元组模仿队列，将像素的坐标值入队
1、从左到右，从上到下遍历每一个像素，判断该像素的像素值是否为1，并且判断它是否被标记过，如果没有被标记过并且像素值为1，则将该像素的位置入队。
2、查找该像素的8邻域内有没有像素值为1的并且没有被标记过的像素，有的话则给与它与该像素一样的标记，并且将该像素入队。
3、每次判断完一个像素的8邻域之后要记得将队列头加一。
4、队列为空之后即表示一个连通区域标记完成。则换一种标记，将队列置空，接着进行其他像素的判断。

Matlab代码

s=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
   0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0;       %这个矩阵是维基百科中的矩阵
   0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 0 0;
   0 0 0 1 1 1 1 0 0 0 1 1 1 1 0 0 0;
   0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 1 0;
   0 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0;
   0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0;
   0 0 0 0 0 0 1 1 1 1 0 0 1 1 1 1 0;
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];

imshow(mat2gray(s));
[m n]=size(s);
tmp=zeros(m,n);     %标记图像
label=1;
queue_head=1;       %队列头
queue_tail=1;       %队列尾
neighbour=[-1 -1;-1 0;-1 1;0 -1;0 1;1 -1;1 0;1 1];  %和当前像素坐标相加得到八个邻域坐标

for i=2:m-1
    for j=2:n-1
        
        if s(i,j)==1 && tmp(i,j) ==0           
            tmp(i,j)=label;
            q{queue_tail}=[i j];        %用元组模拟队列，当前坐标入列
            queue_tail=queue_tail+1;
            
            while queue_head~=queue_tail
                pix=q{queue_head};                
                for k=1:8               %8邻域搜索
                    pix1=pix+neighbour(k,:);
                    if pix1(1)>=2 && pix1(1)<=m-1 && pix1(2) >=2 &&pix1(2)<=n-1  %边界条件的限定
                        if s(pix1(1),pix1(2)) == 1 && tmp(pix1(1),pix1(2)) ==0  %如果当前像素邻域像素为1并且标记图像的这个邻域像素没有被标记，那么标记
                          tmp(pix1(1),pix1(2))=label;
                          q{queue_tail}=[pix1(1) pix1(2)];
                          queue_tail=queue_tail+1;
                        end
                    end
                end
                queue_head=queue_head+1;
            end
            
            clear q;                %清空队列，为新的标记做准备
            label=label+1;
            queue_head=1;
            queue_tail=1;            
        end
    
    end
end
figure,imshow(mat2gray(tmp))