数字信号处理实验（三）：离散时间傅里叶变换

1.dfdt

function X =dtft(x,n,w)
%计算离散时间付里叶变换
%[X]=dtft(x,n,w)
%X=在w频率点上的DTFT数组
%x=n点有限长度序列
%n=样本位置向量
%w=频率点位置向量
X=x*(exp(-j).^(n'*w)); 

2.idfdt

function[x]=idtft(X,n,w)
%计算离散时间付里叶变换
%[X]=dtft(x,n,w)
%X=在w频率点上的DTFT数组
%x=n点有限长度序列
%n=样本位置向量
%w=频率点位置向量
x=1/(2*pi)*X*(exp(j).^(w'*n)); 

3.sigfold

function [y, n] = sigfold(x, n)
y = fliplr(x);
n = -fliplr(n);

4.sigshift

function [y,n] = sigshift(x,m,n0)
% 实现 y(n) = x(n-n0)
% -------------------------
% [y,n] = sigshift(x,m,n0)
%
n = m+n0; y = x;

5.绘制dtft的幅度、相角、实部、虚部

%% (a)
n=0:20;
x=2*(0.8).^n;
w=0:pi/500:pi;
X=dtft(x,n,w)
magX=abs(X);
angX=angle(X);
realX=real(X);
imagX=imag(X);
figure(1)
subplot(2,2,1);
plot(w/pi,magX);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,3);plot(w/pi,angX);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
subplot(2,2,2);plot(w/pi,realX);grid
xlabel('以pi为单位的频率');title('实部');ylabel('实部')
subplot(2,2,4);plot(w/pi,imagX);grid
xlabel('以pi为单位的频率');title('虚部');ylabel('虚部')

6.dtft的性质验证

%% 3
n=0:10;
x1=rand(1,length(n));
x2=rand(1,length(n));
x=x1;
w=0:pi/500:pi;
X1=dtft(x1,n,w);
X2=dtft(x2,n,w);
X=dtft(x,n,w);
%% 线性
a=0.3;
b=0.7;
F1=dtft(a*x1+b*x2,n,w);
F2=a*X1+b*X2;
magF1=abs(F1);
angF1=angle(F1);
magF2=abs(F2);
angF2=angle(F2);
figure(1)
subplot(2,2,1);
plot(w/pi,magF1);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,3);plot(w/pi,angF1);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
subplot(2,2,2);
plot(w/pi,magF2);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,4);plot(w/pi,angF2);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
%% 时移
k=5;
%F1=dtft(x,n-k,w);
F2=exp(-j*w*k).*X1;
y2=idtft(F2,n,w);
%[y1,n1]=sigshift(x,n,k);
%n2=n;
subplot(2,1,1);stem(n,x,'r.'),title('原始时域波形') % 绘出x(jw)
subplot(2,1,2);stem(n2,y2,'r.'),title('平移后时域波形') % 绘出x(jw)
%% 频移
w0=pi/3;
F1=dtft(x.*exp(j*w0*n),n,w);
F2=dtft(x,n,w);
magF1=abs(F1);
angF1=angle(F1);
magF2=abs(F2);
angF2=angle(F2);
figure(3)
subplot(2,2,1);
plot(w/pi,magF1);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,3);plot(w/pi,angF1);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
subplot(2,2,2);
plot(w/pi,magF2);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,4);plot(w/pi,angF2);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
%% 共轭
F1=X1;
F2=conj(dtft(x,n,-w));
magF1=abs(F1);
angF1=angle(F1);
magF2=abs(F2);
angF2=angle(F2);
figure(4)
subplot(2,2,1);
plot(w/pi,magF1);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,3);plot(w/pi,angF1);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
subplot(2,2,2);
plot(w/pi,magF2);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,4);plot(w/pi,angF2);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
%% 折叠
F1=dtft(x,-n,w);
F2=dtft(x,n,-w);
magF1=abs(F1);
angF1=angle(F1);
magF2=abs(F2);
angF2=angle(F2);
figure(5)
subplot(2,2,1);
plot(w/pi,magF1);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,3);plot(w/pi,angF1);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
subplot(2,2,2);
plot(w/pi,magF2);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,4);plot(w/pi,angF2);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')
%% 对称
[xf,n2]=sigfold(x,n);
n3=-10:10;
xe=1/2*[xf(1:10) xf(11)+x(11) x(2:11)];%奇对称分量
F1=dtft(xe,n3,w);
F2=real(X);
realF1=real(F1);
realF2=real(F2);
figure(6)
subplot(2,2,1);plot(w/pi,realF1);grid
xlabel('以pi为单位的频率');title('实部');ylabel('实部')
subplot(2,2,2);plot(w/pi,realF2);grid
xlabel('以pi为单位的频率');title('实部');ylabel('实部')
xo=1/2*[-xf(1:10) -xf(11)+x(11) x(2:11)];%偶对称分量
F1=dtft(xo,n3,w);
F2=j*imag(X);
imagF1=imag(F1);
imagF2=imag(F2);
figure(7)
subplot(2,2,3);plot(w/pi,imagF1);grid
xlabel('以pi为单位的频率');title('虚部');ylabel('虚部')
subplot(2,2,4);plot(w/pi,imagF2);grid
xlabel('以pi为单位的频率');title('虚部');ylabel('虚部')

7.

w=0:pi/500:pi;
H=1./(1-0.8*exp(-j*w));
magH=abs(H);
angH=angle(H);
figure(1)
subplot(1,2,1);plot(w/pi,magH);grid
xlabel('以pi为单位的频率');title('幅频特性');ylabel('幅度')
subplot(1,2,2);plot(w/pi,angH);grid
xlabel('以pi为单位的频率');title('相频特性');ylabel('相位')

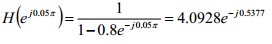
b=1;a=[1,-0.8]; % 输入系数矩阵
n=[0:100];x=cos(0.05*pi*n); % 输入激励序列
y_zs=filter(b,a,x); % 计算响应序列
subplot(2,1,1);stem(n,x,'.'); grid % 画出激励枝干图
xlabel('n');ylabel('x(n)');title('Input sequence');
subplot(2,1,2);stem(n,y_zs,'.'); grid % 画出响应枝干图
xlabel('n');ylabel('y_zs(n)');title('Output sequence');

8.采样和重构

%% 5 a
Dt=0.00005; % 模拟时间间隔：在特定精度下信号为模拟的
t=-0.005:Dt:0.005; % 模拟时刻序列
xa=exp(-1000*abs(t)); % 在特定精度下，由离散信号逼近模拟信号
fs=5000;
Ts=1/fs; % 采样周期
n=-25:1:25; % 离散时间索引
x1=exp(-1000*abs(n*Ts)); % Fs=5000 样本/s:x1为采样后的离散时间序列
K=500; % 对pi进行K等分:相当于对单位圆2pi进行1000等分
dk = pi/K; % pi 的等分步进索引
w=0 : dk : pi; % 角度步进索引
X=x1 * exp(-j* n'*w);% 对x1序列做离散傅立叶变换 
Xr=real(X);
w=[-fliplr(w),w(2:end)]; % 定义w负半轴
Xr=[fliplr(Xr),Xr(2:end)]; % 由于实部偶对称，得到Xr的负半轴
figure(1);
subplot(2,1,1);plot(t*1000,xa);hold on % 绘出xa
stem(n*Ts*1000,x1,'r.'),hold off,title('时域波形') % 绘出x(jw)
subplot(2,1,2);plot(w/pi,Xr);title('频域波形') % 绘出以pi归一化的数字频率对应的频域实部波形
%% 5 c fs=5000重构
Ts=0.0002; % 采样间隔
Fs=1/Ts; % 采样频率
n=-25:1:25; % 采样时间索引
nTs=n*Ts; % 序列时刻索引
Dt=0.00005; % 模拟时刻精度
t=-0.005:Dt:0.005; % 模拟时刻索引
xa= x1* ... % 内插重构
sinc(Fs*(ones(length(nTs),1)*t-nTs'*ones(1,length(t))));
figure(3);
subplot(2,1,1),plot(t*1000,xa, 'k' ),hold on
stem(n*Ts*1000,x1, 'r.' ),hold off ,title('重构波形(不失真)' )

9.

%% 6 (1)a
Dt=0.00005; % 模拟时间间隔：在特定精度下信号为模拟的
t=-0.005:Dt:0.005; % 模拟时刻序列
xa=sin(1000*pi*t); % 在特定精度下，由离散信号逼近模拟信号
Ts=0.0001; % 采样周期
n=-25:1:25; % 离散时间索引
x1=sin(1000*pi*abs(n*Ts)); % Fs=5000 样本/s:x1为采样后的离散时间序列
K=500; % 对pi进行K等分:相当于对单位园2pi进行1000等分
dk = pi/K; % pi 的等分步进索引
w=0 : dk : pi; % 角度步进索引
X=x1 * exp(-j* n'*w);% 对x1序列做离散傅立叶变换 
Xr=real(X);
w=[-fliplr(w),w(2:end)]; % 定义w负半轴
Xr=[fliplr(Xr),Xr(2:end)]; % 由于实部偶对称，得到Xr的负半轴
figure();
subplot(2,2,1);plot(t*1000,xa);hold on % 绘出xa
stem(n*Ts*1000,x1,'r.'),hold off,title('时域波形') % 绘出x(jw)
subplot(2,2,2);plot(w/pi,Xr);title('频域波形') % 绘出以pi归一化的数字频率对应的频域实部波形
magXr=abs(Xr);
angXr=angle(Xr);
subplot(2,2,3);
plot(w/pi,magXr);grid
xlabel('以pi为单位的频率');title('幅度部分');ylabel('幅度')
subplot(2,2,4);plot(w/pi,angXr);grid
xlabel('以pi为单位的频率');title('相角部分');ylabel('弧度')

%% 6 (2)a
Dt=0.00005; % 模拟时间间隔：在特定精度下信号为模拟的
t=0:Dt:1; % 模拟时刻序列
xa=sin(20*pi*t+pi/4); % 在特定精度下，由离散信号逼近模拟信号
Ts=0.05; % 采样周期
n=0:1:20; % 离散时间索引
x1=sin(20*pi*abs(n*Ts)+pi/4); % Fs=5000 样本/s:x1为采样后的离散时间序列
K=500; % 对pi进行K等分:相当于对单位园2pi进行1000等分
dk = pi/K; % pi 的等分步进索引
w=0 : dk : pi; % 角度步进索引
X=x1 * exp(-j* n'*w);% 对x1序列做离散傅立叶变换 
Xr=real(X);
w=[-fliplr(w),w(2:end)]; % 定义w负半轴
Xr=[fliplr(Xr),Xr(2:end)]; % 由于实部偶对称，得到Xr的负半轴
figure();
plot(t,xa);hold on % 绘出xa
stem(n*Ts,x1,'o'),hold off,title('时域波形') % 绘出x(jw)
%% 6 (2)b
Ts=0.05; % 采样间隔
Fs=1/Ts; % 采样频率
n=0:1:20; % 采样时间索引
nTs=n*Ts; % 序列时刻索引
Dt=0.001; % 模拟时刻精度
t=0:Dt:1; % 模拟时刻索引
xa= x1* ... % 内插重构
sinc(Fs*(ones(length(nTs),1)*t-nTs'*ones(1,length(t))));
figure();
plot(t,xa, 'k' ),hold on
stem(n*Ts,x1, 'r.' ),hold off ,title('重构波形(不失真)' )