概述
阵列导向矢量（Steering vector）详细推导
在毫米波信道模型中，常见的建模方式为Saleh-Valenzuela信道模型，其涉及天线阵列的导向矢量，其实描述的是相邻接收天线之间的信号相位差，相位差进一步通过路程差反应出来，本文推导出均匀线阵（ULA）和均匀平面阵（UPA）天线阵列的steering vector:
ULA：
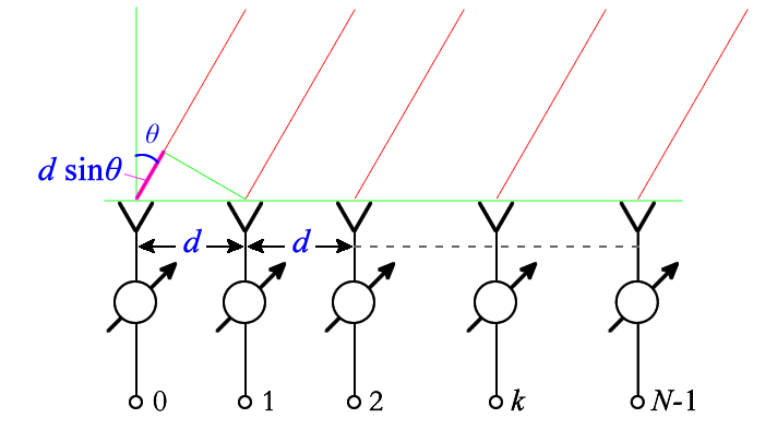
相邻天线间的间距为
d
d
d,入射夹角为
θ
theta
θ,则路程差如图为
d
∗
s
i
n
(
θ
）
d*sin(theta）
d∗sin(θ）,相位差则为
2
π
d
s
i
n
(
θ
)
/
λ
2pi dsin(theta)/lambda
2πdsin(θ)/λ,以左边第一个天线为参考点，steering vector 表示为：
a
=
[
1
,
e
j
2
π
λ
d
sin
(
θ
)
,
.
.
.
,
e
j
2
π
λ
d
(
N
−
1
)
sin
(
θ
)
]
T
a = {[1,{e^{jfrac{{2pi }}{lambda }dsin left( theta right)}},...,{e^{jfrac{{2pi }}{lambda }dleft( {N - 1} right)sin left( theta right)}}]^T}
a=[1,ejλ2πdsin(θ),...,ejλ2πd(N−1)sin(θ)]T
其中
N
N
N为天线个数。
UPA：
结论如下：对于长为
N
Z
N_Z
NZ,宽为
N
Y
N_Y
NY的UPA天线，其对应方位角为
φ
varphi
φ，仰角为
θ
theta
θ,相邻天线间间距为
d
d
d,其导向矢量为
a
=
a
z
⊗
a
y
a = {a_z} otimes {a_y}
a=az⊗ay，其中：
a
z
=
[
1
,
e
j
2
π
λ
d
sin
(
θ
)
,
.
.
.
,
e
j
2
π
λ
d
(
N
Z
−
1
)
sin
(
θ
)
]
T
{a_z} = {[1,{e^{jfrac{{2pi }}{lambda }dsin left( theta right)}},...,{e^{jfrac{{2pi }}{lambda }dleft( {{N_Z} - 1} right)sin left( theta right)}}]^T}
az=[1,ejλ2πdsin(θ),...,ejλ2πd(NZ−1)sin(θ)]T
a
y
=
[
1
,
e
j
2
π
λ
d
sin
(
φ
)
cos
(
θ
)
,
.
.
.
,
e
j
2
π
λ
d
(
N
Y
−
1
)
sin
(
φ
)
cos
(
θ
)
]
T
{a_y} = {[1,{e^{jfrac{{2pi }}{lambda }dsin left( varphi right)cos left( theta right)}},...,{e^{jfrac{{2pi }}{lambda }dleft( {{N_Y} - 1} right)sin left( varphi right)cos left( theta right)}}]^T}
ay=[1,ejλ2πdsin(φ)cos(θ),...,ejλ2πd(NY−1)sin(φ)cos(θ)]T
Remark: 由于方位角及仰角的定义不同，阵列矢量通常不同，视情况而定。
推导如下：
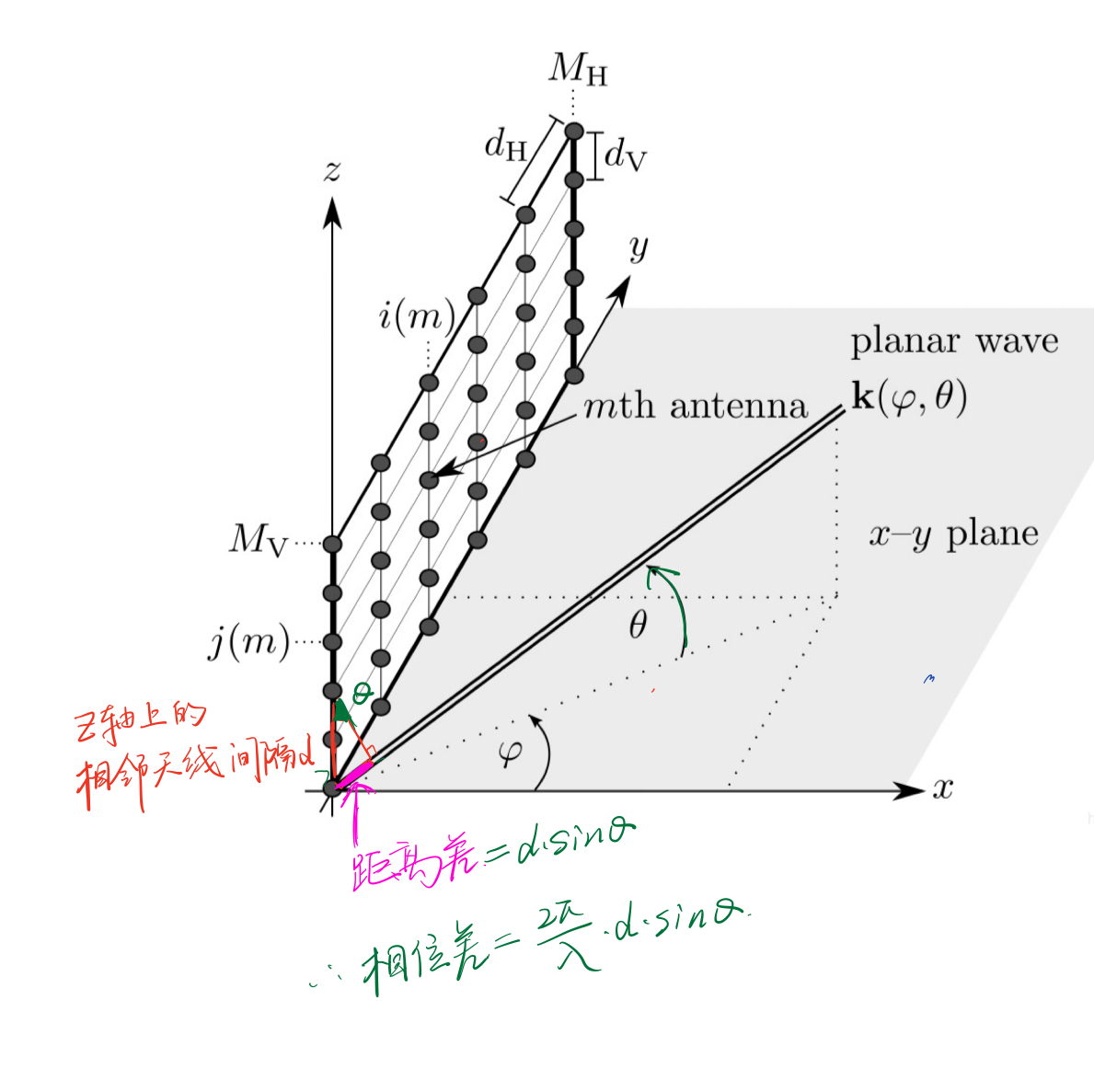
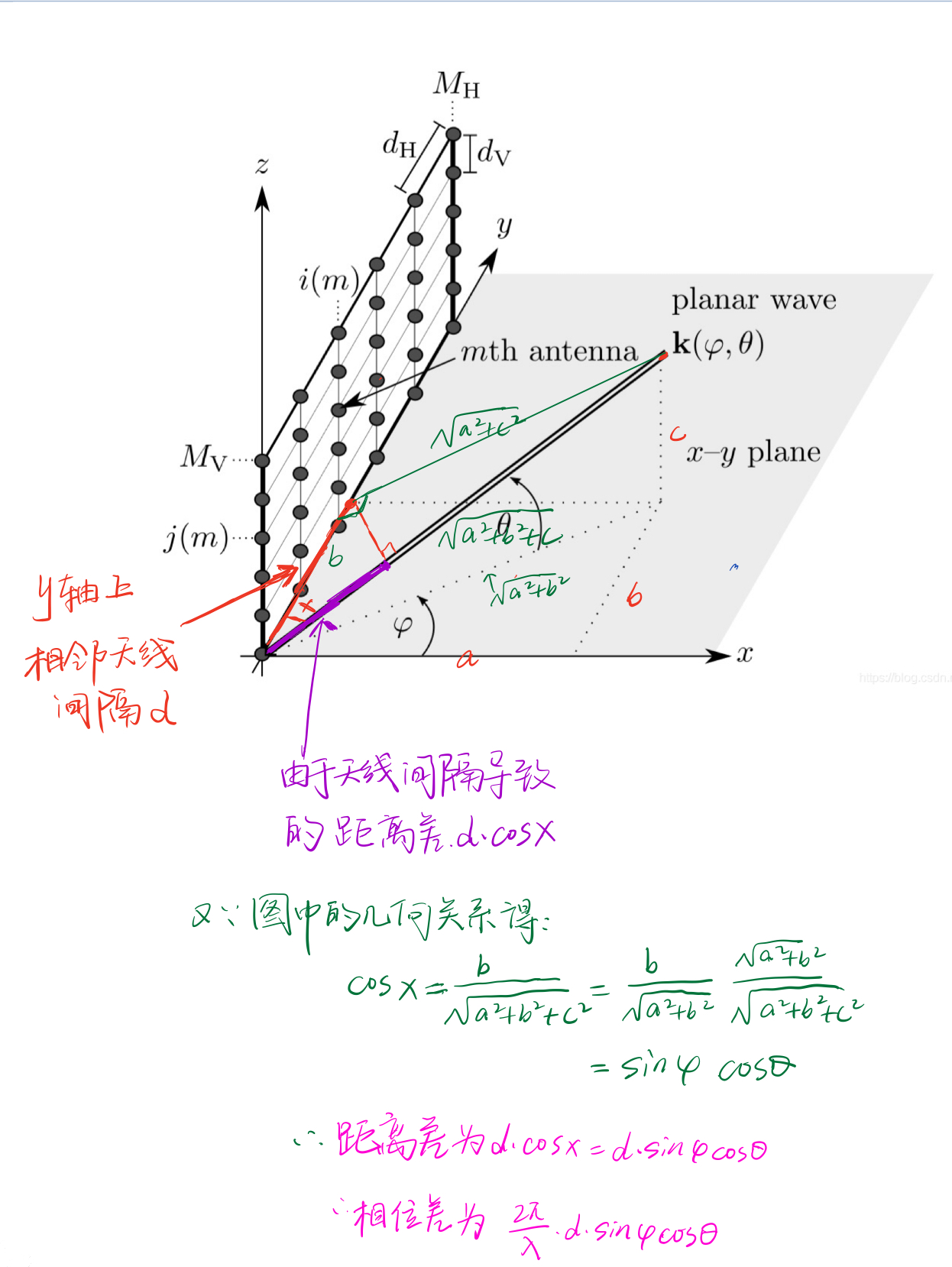
最后
以上就是美好大米为你收集整理的阵列导向矢量（Steering vector）推导阵列导向矢量（Steering vector）详细推导的全部内容，希望文章能够帮你解决阵列导向矢量（Steering vector）推导阵列导向矢量（Steering vector）详细推导所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复