概述
决策树（Decision Tree,简称：DT）
决策树精选幕布 @转载
基本的介绍：
顾名思义，决策树这个名字可以分为两部分：决策和树。
决策规则：
分类（离散值）：样本标签少数服从多数
回归（连续值）：所有样本的均值
树：这个算法模型是以树状的形态进行表示的。
决策树是一个有监督算法，它既可以作为分类算法，也可以作为回归算法。
决策树的生成只考虑局部最优，相对的，决策树剪枝则考虑全局最优。
概念：
决策树：是一种树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果，本质是一棵由多个判断节点组成的树。
常见的决策树类型：
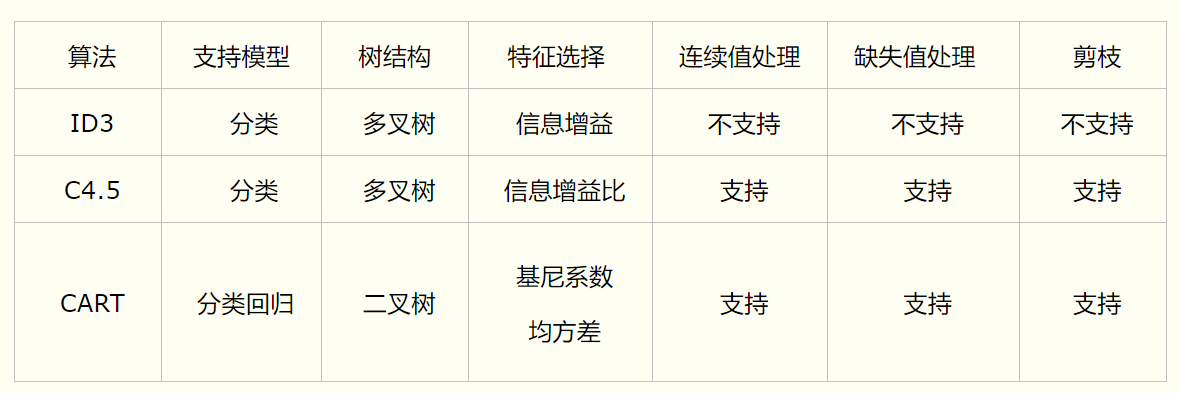
所以接下来介绍一些决策树算法，将从以下5个方面来介绍：
ID3
C4.5
CART
剪枝
决策树的优缺点
ID3的定义
ID3算法是1986年由Quinlan首先提出的，该算法是以信息论为基础，以信息熵和信息增益为衡量标准，从而实现对数据的归纳分类。是生成最小的树型结构，而是一个启发式算法。
1. 信息熵
简介：熵这个概念最早起源于物理学，在物理学中是用来度量一个热力学系统的无序程度，而在信息学里面，熵是对不确定性的度量。在1986年，香农引入了信息熵，将其定义为离散随机事件出现的概率，一个系统越是有序，信息熵就越低，反之一个系统越是混乱，它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。
公式：
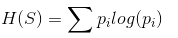
其中pi为第i个类别的概率，S是样例集合
举例：
全部的西瓜数据集共有17个好坏样本。
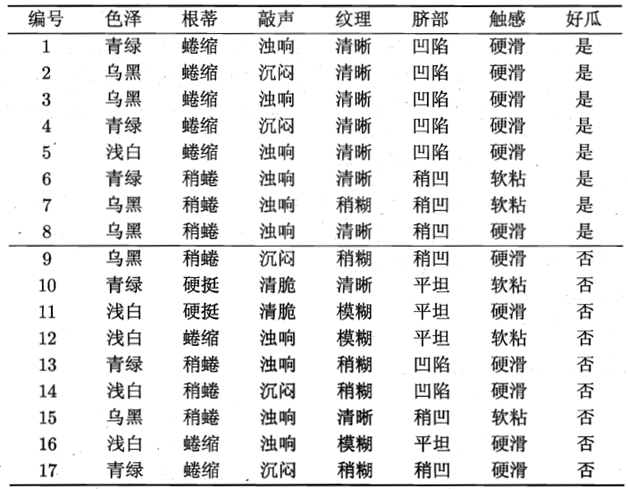
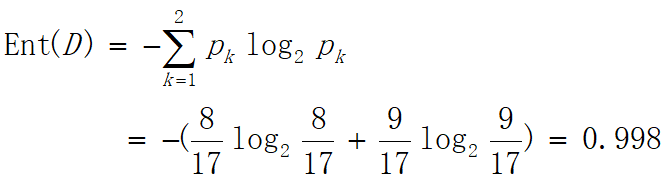
即香浓熵为： 0.998
2. 信息增益
公式：
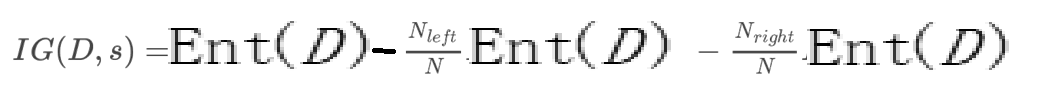
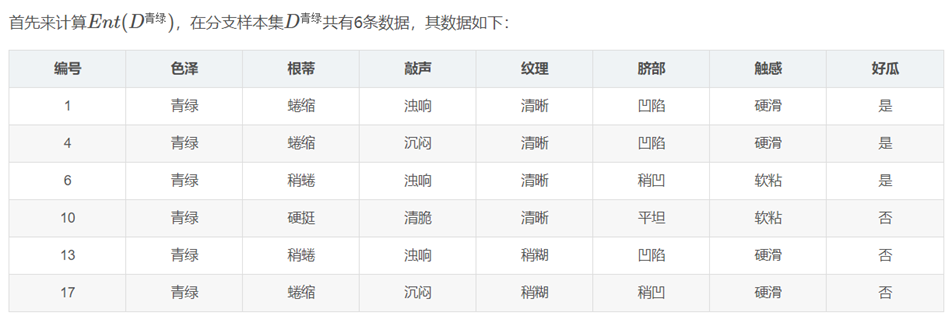
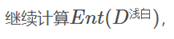
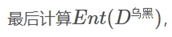
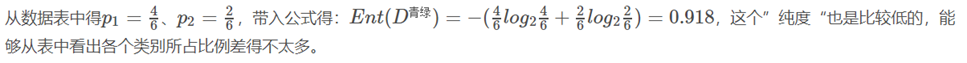
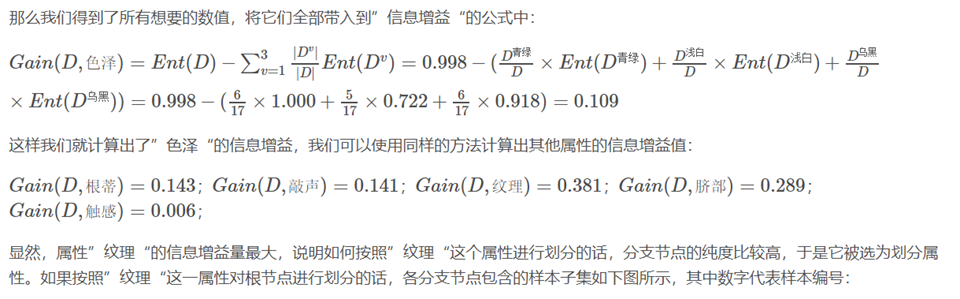
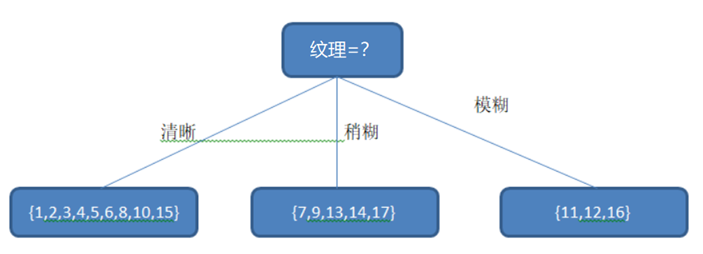
在这里根蒂、脐部、触感三个属性均取得了最大的信息增益，可任取其中之一作为划分属性，再次划分得到子分支。
就这样不断的划分，直到遇到终止条件：
当前节点包含的样本全属于同一类别，无需划分；
当前属性集为空，或是所有样本再所有属性上取值相同，无法划分；
当前节点集合包含的样本集合为空，不能划分。
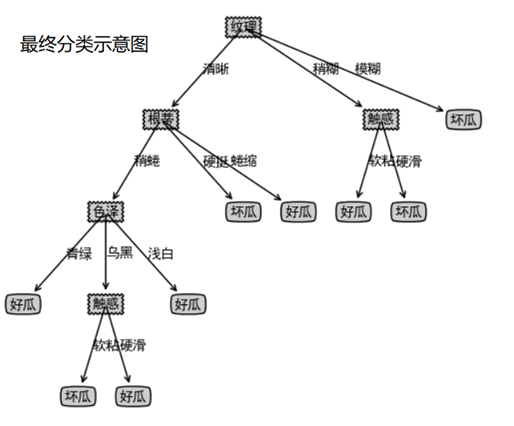
总结：
ID3算法的核心是在决策树各个子节点上应用信息增益准则选择特征，递归的构建决策树，具体方法是:从根节点开始，对节点计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的特征，由该特征的不同取值建立子节点；再对子节点递归调用以上方法，构建决策树。
ID3算法只有树的生成，所以该算法生成的树容易产生过拟合，分得太细，考虑条件太多。
ID3 算法的缺点
1.用信息增益选择属性时偏向于选择分枝比较多的属性值，即取值 多的属性。
2.不能处理连续属性。
C4.5的定义
C4.5算法与ID3算法相似，C4.5算法对ID3算法进行了改进。
CART的定义
CART（classification and regression tree）：分类与回归树，既可以用于分类也可以用于回归。
常见决策树类型及剪枝
1为什么要剪枝
一般情况下，决策树会将模型分成最优的形式，所以会导致过拟合现象的发生，所以进行剪枝处理
原因1： 噪声、 样本冲突， 即错误的样本数据。
原因2： 特征即属性不能完全作为分类标准。
原因3： 巧合的规律性， 数据量不够大。
2常用的剪枝方法
**预剪枝：**提前处理，计算量小
主要有三种：
（1）每一个结点所包含的最小样本数目，例如10，则该结点总样本数小于10时，则不再分；
（2）指定树的高度或者深度，例如树的最大深度为4；
（3）指定结点的熵小于某个值，不再划分。随着树的增长， 在训练样集上的精度是调上升的， 然而在独立的测试样例上测出的精度先上升后下降。
后剪枝，在已生成过拟合决策树上进行剪枝，可以避免欠拟合，计算量大。
主要有四种：
（1）REP-错误率降低剪枝
（2）PEP-悲观剪枝
（3）CCP-代价复杂度剪枝
（4）MEP-最小错误剪枝
结论：
决策树的剪枝，由于生成的决策树存在过拟合问题，需要对它进行剪枝，以简化后学到的决策树。决策树的剪枝，往往从已生成的树上剪掉一些叶节点或叶节点以上的子树，并将其父节点或根节点作为新的叶节点，从而简化生成的决策树模型。
ID3不能剪枝
C4.5和CRAT都可以剪枝
决策树的优缺点
决策树的优点：
（1）具有可读性，如果给定一个模型，那么过呢据所产生的决策树很容易推理出相应的逻辑表达。
（2）分类速度快，能在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
决策树的缺点：
（1）对未知的测试数据未必有好的分类、泛化能力，即容易发生过拟合现象，此时可采用剪枝或随机森林。
最后
以上就是斯文老虎为你收集整理的决策树（Decision Tree）总结决策树（Decision Tree,简称：DT）的全部内容，希望文章能够帮你解决决策树（Decision Tree）总结决策树（Decision Tree,简称：DT）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复