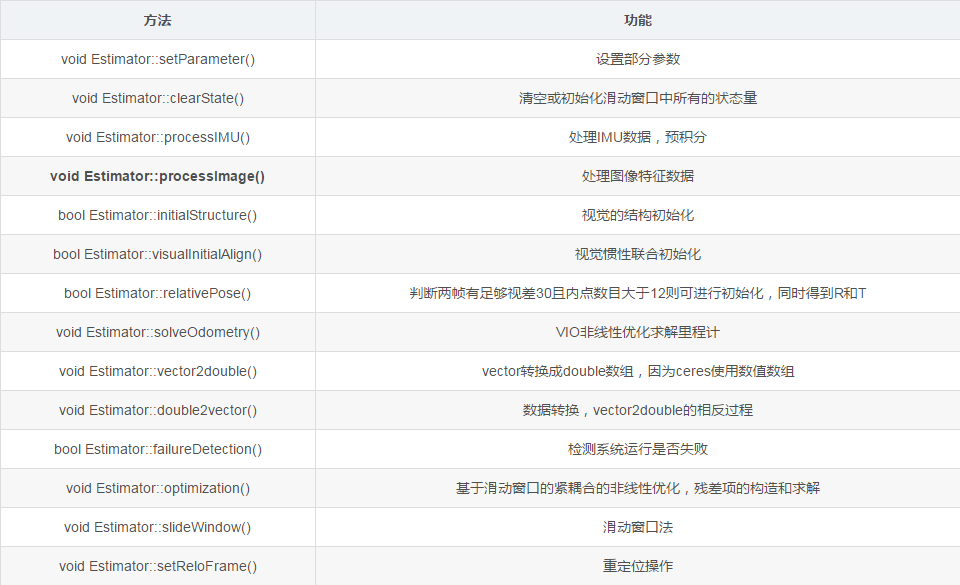
Estimator类
目录
processImage()函数
initialStructure()初始化函数
SFM初始化
relativePose()函数
getCorresponding()函数返回两帧匹配特征点3D坐标
solveRelativeRT()函数 利用五点法求解相机初始位姿
GlobalSFM::construct () 最重要的函数!!!坚持就是胜利
processImage()函数
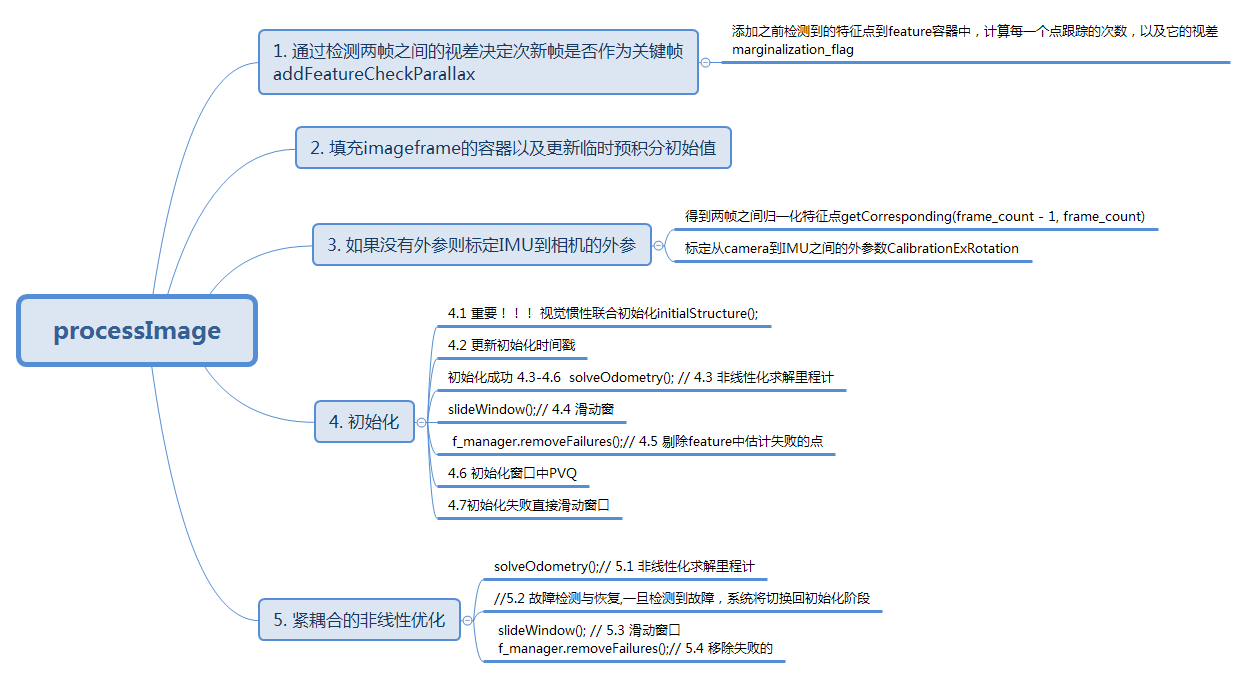
1.检查两帧的视差判断是否为关键帧f_manager.addFeatureCheckParallax()在 VINS-Mono 代码详细解读——feature_manager.cpp中已经解释
2.IMU预积分 IntegrationBase 在 VINS-Mono 代码详细解读——IMU离散中值预积分 中解释
3.在线标定外参 CalibrationExRotation 在 VINS-Mono 代码详细解读——基础储备:在线Cam到IMU的外参标定 InitialEXRotation类 中已经解释
本节将重点介绍初始化部分。
/**
* @brief 处理图像特征数据
* @Description addFeatureCheckParallax()添加特征点到feature中,计算点跟踪的次数和视差,判断是否是关键帧
* 判断并进行外参标定
* 进行视觉惯性联合初始化或基于滑动窗口非线性优化的紧耦合VIO
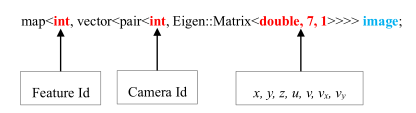
* @param[in] image 某帧所有特征点的[camera_id,[x,y,z,u,v,vx,vy]]s构成的map,索引为feature_id
* @param[in] header 某帧图像的头信息
* @return void
*/
void Estimator::processImage(const map<int, vector<pair<int, Eigen::Matrix<double, 7, 1>>>> &image, const std_msgs::Header &header)
{
ROS_DEBUG("new image coming ------------------------------------------");
ROS_DEBUG("Adding feature points %lu", image.size());
// 1. 通过检测两帧之间的视差决定次新帧是否作为关键帧
if (f_manager.addFeatureCheckParallax(frame_count, image, td))//添加之前检测到的特征点到feature容器中,计算每一个点跟踪的次数,以及它的视差
marginalization_flag = MARGIN_OLD;//=0
else
marginalization_flag = MARGIN_SECOND_NEW;//=1
ROS_DEBUG("this frame is--------------------%s", marginalization_flag ? "reject" : "accept");
ROS_DEBUG("%s", marginalization_flag ? "Non-keyframe" : "Keyframe");
ROS_DEBUG("Solving %d", frame_count);
ROS_DEBUG("number of feature: %d", f_manager.getFeatureCount());
Headers[frame_count] = header;
// 2. 填充imageframe的容器以及更新临时预积分初始值
ImageFrame imageframe(image, header.stamp.toSec());//ImageFrame类包括特征点、时间、位姿Rt、预积分对象pre_integration、是否关键帧
imageframe.pre_integration = tmp_pre_integration;// tmp_pre_integration是之前IMU 预积分计算的
all_image_frame.insert(make_pair(header.stamp.toSec(), imageframe));// map<double, ImageFrame> all_image_frame;
tmp_pre_integration = new IntegrationBase{acc_0, gyr_0, Bas[frame_count], Bgs[frame_count]};//更新临时预积分初始值
// 3. 如果没有外参则标定IMU到相机的外参
if(ESTIMATE_EXTRINSIC == 2)
{
ROS_INFO("calibrating extrinsic param, rotation movement is needed");
if (frame_count != 0)
{
//得到两帧之间归一化特征点
vector<pair<Vector3d, Vector3d>> corres = f_manager.getCorresponding(frame_count - 1, frame_count);
Matrix3d calib_ric;
//标定从camera到IMU之间的外参数
if (initial_ex_rotation.CalibrationExRotation(corres, pre_integrations[frame_count]->delta_q, calib_ric))
{
ROS_WARN("initial extrinsic rotation calib success");
ROS_WARN_STREAM("initial extrinsic rotation: " << endl << calib_ric);
ric[0] = calib_ric;
RIC[0] = calib_ric;
ESTIMATE_EXTRINSIC = 1;// 完成外参标定
}
}
}
// 4. 初始化
if (solver_flag == INITIAL)//初始化
{
//frame_count是滑动窗口中图像帧的数量,一开始初始化为0,滑动窗口总帧数WINDOW_SIZE=10
//确保有足够的frame参与初始化
if (frame_count == WINDOW_SIZE)
{
bool result = false;
//有外参且当前帧时间戳大于初始化时间戳0.1秒,就进行初始化操作
if( ESTIMATE_EXTRINSIC != 2 && (header.stamp.toSec() - initial_timestamp) > 0.1)
{
// 4.1 重要!!! 视觉惯性联合初始化
result = initialStructure();
// 4.2 更新初始化时间戳
initial_timestamp = header.stamp.toSec();
}
if(result)//初始化成功
{
// 先进行一次滑动窗口非线性优化,得到当前帧与第一帧的位姿
solver_flag = NON_LINEAR;// 初始化更改为非线性
solveOdometry(); // 4.3 非线性化求解里程计
slideWindow();// 4.4 滑动窗
f_manager.removeFailures();// 4.5 剔除feature中估计失败的点(solve_flag == 2)0 haven't solve yet; 1 solve succ; 2 solve fail;
ROS_INFO("Initialization finish!");
// 4.6 初始化窗口中PVQ
last_R = Rs[WINDOW_SIZE];
last_P = Ps[WINDOW_SIZE];
last_R0 = Rs[0];
last_P0 = Ps[0];
}
else
slideWindow();// 初始化失败则直接滑动窗口
}
else
frame_count++;// 图像帧数量+1
}
else// 5. 紧耦合的非线性优化
{
TicToc t_solve;
solveOdometry();// 5.1 非线性化求解里程计
ROS_DEBUG("solver costs: %fms", t_solve.toc());
//5.2 故障检测与恢复,一旦检测到故障,系统将切换回初始化阶段
if (failureDetection())
{
ROS_WARN("failure detection!");
failure_occur = 1;
clearState();// 清空状态
setParameter();// 重设参数
ROS_WARN("system reboot!");
return;
}
TicToc t_margin;
slideWindow(); // 5.3 滑动窗口
f_manager.removeFailures();// 5.4 移除失败的
ROS_DEBUG("marginalization costs: %fms", t_margin.toc());
// prepare output of VINS
key_poses.clear();
for (int i = 0; i <= WINDOW_SIZE; i++)
key_poses.push_back(Ps[i]);// 关键位姿的位置 Ps
last_R = Rs[WINDOW_SIZE];
last_P = Ps[WINDOW_SIZE];
last_R0 = Rs[0];
last_P0 = Ps[0];
}
}
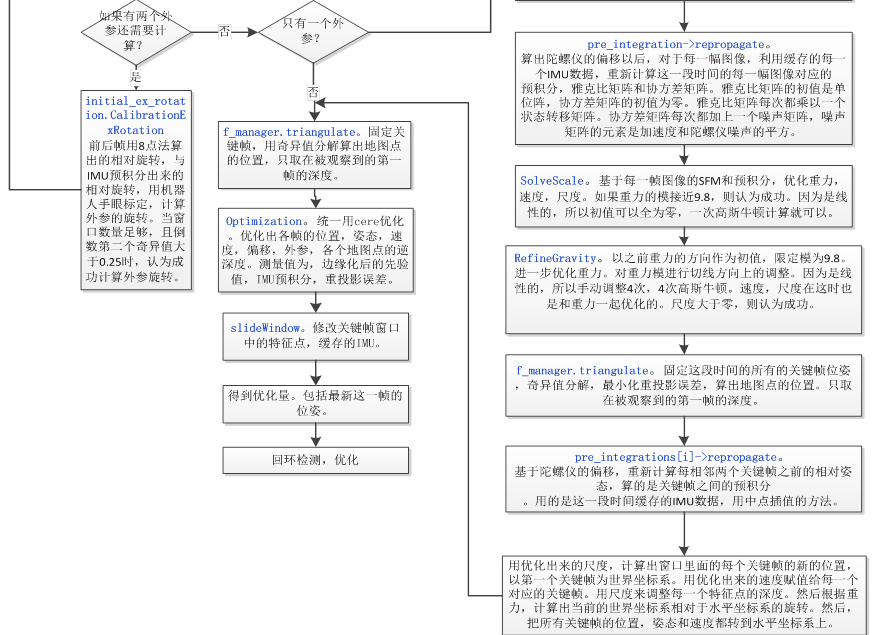
initialStructure()初始化函数
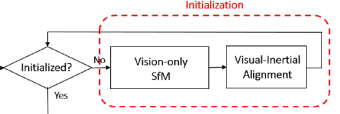
视觉结构初始化过程至关重要,多传感器融合过程中,当单个传感器数据不确定性较高,需要依赖其他传感器降低不确定性。先对纯视觉SFM初始化相机位姿,再和IMU对齐。
主要分为1、纯视觉SFM估计滑动窗内相机位姿和路标点逆深度。2、视觉惯性联合校准,SFM与IMU积分对齐。


代码部分

首先纯视觉SFM初始化sfm.construct()函数,之后视觉惯性联合初始化visualInitialAlign()函数。
视觉初始化入口在
bool Estimator::initialStructure()
初始化变量
Quaterniond Q[frame_count + 1];//旋转四元数Q
Vector3d T[frame_count + 1]; // 平移矩阵T
map<int, Vector3d> sfm_tracked_points; //存储SFM重建出特征点的坐标
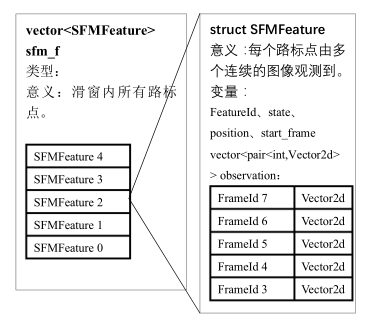
vector<SFMFeature> sfm_f;// SFMFeature三角化状态、特征点索引、平面观测、位置坐标、深度首先定义视觉SFM最重要的几个变量,旋转Q和平移T,map容器sfm_tracked_points保存SFM重建出的路标3D坐标,最重要的是SFMFeature类型的vector容器sfm_f。SFMFeature数据结构为:
// SFM 数据结构
struct SFMFeature
{
bool state;//特征点的状态(是否被三角化)
int id;//特征点ID
vector<pair<int,Vector2d>> observation;//所有观测到该特征点的图像帧ID和 2D像素坐标
double position[3];//路标3D坐标
double depth;//深度
};SFM初始化
1、通过加速度标准差保证IMU有充分运动激励,可以初始化
// 1. 通过加速度标准差判断IMU是否有充分运动以初始化。
{
map<double, ImageFrame>::iterator frame_it;// 迭代器
// 1.1 先求均值 aver_g
Vector3d sum_g;
for (frame_it = all_image_frame.begin(), frame_it++; frame_it != all_image_frame.end(); frame_it++)
{
double dt = frame_it->second.pre_integration->sum_dt;
Vector3d tmp_g = frame_it->second.pre_integration->delta_v / dt;
sum_g += tmp_g;
}
Vector3d aver_g;
aver_g = sum_g * 1.0 / ((int)all_image_frame.size() - 1);// 总帧数减1,因为all_image_frame第一帧不算
// 1.2 再求标准差var,表示线加速度的标准差
double var = 0;
for (frame_it = all_image_frame.begin(), frame_it++; frame_it != all_image_frame.end(); frame_it++)
{
double dt = frame_it->second.pre_integration->sum_dt;
Vector3d tmp_g = frame_it->second.pre_integration->delta_v / dt;
var += (tmp_g - aver_g).transpose() * (tmp_g - aver_g);
//cout << "frame g " << tmp_g.transpose() << endl;
}
var = sqrt(var / ((int)all_image_frame.size() - 1));
//ROS_WARN("IMU variation %f!", var);
// 判断,加速度标准差大于0.25则代表imu充分激励,足够初始化
if(var < 0.25)
{
ROS_INFO("IMU excitation not enouth!");
//return false;
}
}求解标准差的过程需要先求解均值,再求每个值和均值的差,最后需要判断加速度标准差大于0.25即可满足imu充分激励,可以初始化。
ImageFrame图像帧的数据结构为,就是头文件initial_alignment.h全部内容。
image类型为:
class ImageFrame
{
public:
ImageFrame(){};
ImageFrame(const map<int, vector<pair<int, Eigen::Matrix<double, 7, 1>>>>& _points, double _t):t{_t},is_key_frame{false}
{
points = _points;
};
// 图像特征点points,map第一索引是camera_id,内部第二层索引是feaure_id
map<int, vector<pair<int, Eigen::Matrix<double, 7, 1>> > > points;
double t;// ???
Matrix3d R;// 相机位姿
Vector3d T;
IntegrationBase *pre_integration;// IMU预积分
bool is_key_frame;// 是否关键帧
};IntergrationBase积分类声明为:
class IntegrationBase
{
public:
IntegrationBase() = delete;
// 预积分类:加速度计、陀螺仪、线性加速度计ba、陀螺仪bg、雅克比矩阵初始化、协方差矩阵15*15、dt、PVQ
IntegrationBase(const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
: acc_0{_acc_0}, gyr_0{_gyr_0}, linearized_acc{_acc_0}, linearized_gyr{_gyr_0},
linearized_ba{_linearized_ba}, linearized_bg{_linearized_bg},
jacobian{Eigen::Matrix<double, 15, 15>::Identity()}, covariance{Eigen::Matrix<double, 15, 15>::Zero()},
sum_dt{0.0}, delta_p{Eigen::Vector3d::Zero()}, delta_q{Eigen::Quaterniond::Identity()}, delta_v{Eigen::Vector3d::Zero()}
{
noise = Eigen::Matrix<double, 18, 18>::Zero();
noise.block<3, 3>(0, 0) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(3, 3) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(6, 6) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(9, 9) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(12, 12) = (ACC_W * ACC_W) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(15, 15) = (GYR_W * GYR_W) * Eigen::Matrix3d::Identity();
}all_image_frame类的声明为:
map<double, ImageFrame> all_image_frame;2、将f_manager中的所有feature保存到存有SFMFeature对象的sfm_f中
for (auto &it_per_id : f_manager.feature)// list<FeaturePerId> feature滑动窗口内所有角点
{
int imu_j = it_per_id.start_frame - 1;// 第一次观测到特征点的帧数-1
SFMFeature tmp_feature;
tmp_feature.state = false;// 状态state
tmp_feature.id = it_per_id.feature_id;// 特征点ID
for (auto &it_per_frame : it_per_id.feature_per_frame)
{
imu_j++;
Vector3d pts_j = it_per_frame.point;// 3D特征点坐标
// 所有观测到该特征点的图像帧ID和图像坐标
tmp_feature.observation.push_back(make_pair(imu_j, Eigen::Vector2d{pts_j.x(), pts_j.y()}));
}
sfm_f.push_back(tmp_feature);
} 对SFMFeature类的数据结构进行填充,state、id、observation、position、depth,最终填充到sfm_f中,表示每个特征点对应的所有被观测数据。将特征管理器中的特征信息保存到SFMFeature对象sfm_f中sfm_f.push_back(tmp_feature)3、返回滑动窗口中第一个满足视差的帧,为l帧,以及RT,可以三角化。
f_manager是特征管理器类的对象,具体在上一节feature_manager.cpp文章中
FeatureManager f_manager;//特征管理器类relativePose()函数
if (!relativePose(relative_R, relative_T, l))
{
ROS_INFO("Not enough features or parallax; Move device around");
return false;
}/**
* @brief 返回滑动窗口中第一个满足视差的帧,为l帧,以及RT,可以三角化。
* @Description 判断每帧到窗口最后一帧对应特征点的平均视差是否大于30
solveRelativeRT()通过基础矩阵计算当前帧与第l帧之间的R和T,并判断内点数目是否足够
* @param[out] relative_R 当前帧到第l帧之间的旋转矩阵R
* @param[out] relative_T 当前帧到第l帧之间的平移向量T
* @param[out] L 从第一帧开始到滑动窗口中第一个满足视差足够的帧,这里的l帧之后作为参考帧做全局SFM用
* @return bool 1:可以进行初始化;0:不满足初始化条件
*/
bool Estimator::relativePose(Matrix3d &relative_R, Vector3d &relative_T, int &l)
{
for (int i = 0; i < WINDOW_SIZE; i++)
{
// 寻找第i帧到窗口最后一帧的对应特征点
vector<pair<Vector3d, Vector3d>> corres;
corres = f_manager.getCorresponding(i, WINDOW_SIZE);// 先得到第i帧和最后一帧的特征匹配
if (corres.size() > 20) // 1. 首先corres数目足够
{
// 2. 计算平均视差>30
double sum_parallax = 0;
double average_parallax;
for (int j = 0; j < int(corres.size()); j++)
{
//第j个对应点在第i帧和最后一帧的(x,y)
Vector2d pts_0(corres[j].first(0), corres[j].first(1));
Vector2d pts_1(corres[j].second(0), corres[j].second(1));
double parallax = (pts_0 - pts_1).norm();
sum_parallax = sum_parallax + parallax;
}
average_parallax = 1.0 * sum_parallax / int(corres.size());
//判断是否满足初始化条件:视差>30和内点数满足要求
//同时返回窗口最后一帧(当前帧)到第l帧(参考帧)的Rt
if(average_parallax * 460 > 30 && m_estimator.solveRelativeRT(corres, relative_R, relative_T))
{
l = i;
ROS_DEBUG("average_parallax %f choose l %d and newest frame to triangulate the whole structure", average_parallax * 460, l);
return true;
}
}
}
return false;
}主要目的是找到滑动窗口中第一个与最后一帧具有足够的共视特征以及视差的帧的索引 l,具体方式为在滑动窗内从第一帧开始计算每一帧和最后一帧匹配的特征点corres = f_manager.getCorresponding(i, WINDOW_SIZE);。找到的第l帧作为参考帧,并通过solveRelativeRT(corres, relative_R, relative_T)计算当前帧和最后一帧的相对位姿。这里的R,T是在最后一帧相对于 l 帧坐标系的位姿估计。
getCorresponding()函数返回两帧匹配特征点3D坐标
//得到frame_count_l与frame_count_r两帧之间的对应特征点3D坐标
vector<pair<Vector3d, Vector3d>> FeatureManager::getCorresponding(int frame_count_l, int frame_count_r)
{
vector<pair<Vector3d, Vector3d>> corres;
for (auto &it : feature)// 遍历feature的list容器
{
if (it.start_frame <= frame_count_l && it.endFrame() >= frame_count_r)
{
Vector3d a = Vector3d::Zero(), b = Vector3d::Zero();
int idx_l = frame_count_l - it.start_frame;// 当前帧-第一次观测到特征点的帧数
int idx_r = frame_count_r - it.start_frame;
a = it.feature_per_frame[idx_l].point;
b = it.feature_per_frame[idx_r].point;
corres.push_back(make_pair(a, b));
}
}
return corres;
}又是通过feature的list容器,如果某个特征点能被观测到的第一帧和最后一帧范围大,[start_frame,endFrame()]是个大范围,而滑动窗 [i,WINDOW]被包含进去了,那么可以直接获取特征点的3D坐标。
for (auto &it : feature){
Vector3d a = it.feature_per_frame[idx_l].point;
}solveRelativeRT()函数 利用五点法求解相机初始位姿
- cv::findFundamentalMat() 利用opencv函数求解F矩阵
- cv::recoverPose() 利用opencv函数分解F矩阵,得到相机旋转量、位移量
/**
* @brief 通过求解本质矩阵得到R,t
* @Description findFundamentalMat()采用RANSAC算法求解本质矩阵E
* recoverPose()通过本质矩阵得到Rt
求Rt的对称变换,判断内点数大于12
* @param[in] corres 对应特征点对
* @param[out] Rotation 当前帧到参考帧的旋转矩阵
* @param[out] Translation 当前帧到参考帧的平移向量
* @return bool true:内点数大于12
*/
bool MotionEstimator::solveRelativeRT(const vector<pair<Vector3d, Vector3d>> &corres, Matrix3d &Rotation, Vector3d &Translation)
{
if (corres.size() >= 15)
{
vector<cv::Point2f> ll, rr;
for (int i = 0; i < int(corres.size()); i++)
{
ll.push_back(cv::Point2f(corres[i].first(0), corres[i].first(1)));
rr.push_back(cv::Point2f(corres[i].second(0), corres[i].second(1)));
}
cv::Mat mask;
/**
* Mat cv::findFundamentalMat( 返回通过RANSAC算法求解两幅图像之间的本质矩阵E
* nputArray points1, 第一幅图像点的数组
* InputArray points2, 第二幅图像点的数组
* int method = FM_RANSAC, RANSAC 算法
* double param1 = 3., 点到对极线的最大距离,超过这个值的点将被舍弃
* double param2 = 0.99, 矩阵正确的可信度
* OutputArray mask = noArray() 在计算过程中没有被舍弃的点
* )
*/
cv::Mat E = cv::findFundamentalMat(ll, rr, cv::FM_RANSAC, 0.3 / 460, 0.99, mask);
cv::Mat cameraMatrix = (cv::Mat_<double>(3, 3) << 1, 0, 0, 0, 1, 0, 0, 0, 1);
cv::Mat rot, trans;
/**
* int cv::recoverPose ( 通过本质矩阵得到Rt,返回通过手性校验的内点个数
* InputArray E, 本质矩阵
* InputArray points1, 第一幅图像点的数组
* InputArray points2, 第二幅图像点的数组
* InputArray cameraMatrix, 相机内参
* OutputArray R, 第一帧坐标系到第二帧坐标系的旋转矩阵
* OutputArray t, 第一帧坐标系到第二帧坐标系的平移向量
* InputOutputArray mask = noArray() 在findFundamentalMat()中没有被舍弃的点
* )
*/
int inlier_cnt = cv::recoverPose(E, ll, rr, cameraMatrix, rot, trans, mask);
//cout << "inlier_cnt " << inlier_cnt << endl;
//rr=R*ll+t ll=(R^T)*rr-(R^T)*t
Eigen::Matrix3d R;
Eigen::Vector3d T;
for (int i = 0; i < 3; i++)
{
T(i) = trans.at<double>(i, 0);
for (int j = 0; j < 3; j++)
R(i, j) = rot.at<double>(i, j);
}
//得到窗口最后一帧(当前帧)到第l帧(参考帧)的坐标系变换Rt
Rotation = R.transpose();
Translation = -R.transpose() * T;
if(inlier_cnt > 12)
return true;
else
return false;
}
return false;
}4、对窗口中每个图像帧求解sfm问题
// 4. 对窗口中每个图像帧求解sfm问题
// 得到所有图像帧相对于参考帧l的姿态四元数Q、平移向量T和特征点坐标sfm_tracked_points。
GlobalSFM sfm;
if(!sfm.construct(frame_count + 1, Q, T, l,
relative_R, relative_T,
sfm_f, sfm_tracked_points))
{
// 求解失败则边缘化最早一帧并滑动窗口
ROS_DEBUG("global SFM failed!");
marginalization_flag = MARGIN_OLD;
return false;
}里面用到了GlobalSFM类定义为:intial_sfm.h
/ SFM类
class GlobalSFM
{
public:
GlobalSFM();
bool construct(int frame_num, Quaterniond* q, Vector3d* T, int l,
const Matrix3d relative_R, const Vector3d relative_T,
vector<SFMFeature> &sfm_f, map<int, Vector3d> &sfm_tracked_points);
private:
// PnP得到当前帧相对于第l帧的位姿
bool solveFrameByPnP(Matrix3d &R_initial, Vector3d &P_initial, int i, vector<SFMFeature> &sfm_f);
// 三角化点
void triangulatePoint(Eigen::Matrix<double, 3, 4> &Pose0, Eigen::Matrix<double, 3, 4> &Pose1,
Vector2d &point0, Vector2d &point1, Vector3d &point_3d);
// 三角化两帧
void triangulateTwoFrames(int frame0, Eigen::Matrix<double, 3, 4> &Pose0,
int frame1, Eigen::Matrix<double, 3, 4> &Pose1,
vector<SFMFeature> &sfm_f);
int feature_num; // 特征点数量
};GlobalSFM::construct () 最重要的函数!!!坚持就是胜利
首先看函数声明,为了求解滑动窗内所有图像帧相对于第l帧(参考帧)的位姿和三角化特征点3D坐标。输出所有图像帧相对于参考帧l的姿态四元数Q、平移向量T和特征点坐标,放在sfm_f和sfm_tracked_points内。
/**
* @brief 纯视觉sfm,求解窗口中的所有图像帧相对于第l帧的位姿和三角化的特征点坐标
* @param[in] frame_num 窗口总帧数(frame_count + 1)
* @param[out] q 窗口内图像帧的旋转四元数q(相对于第l帧)Q[frame_count + 1]
* @param[out] T 窗口内图像帧的平移向量T(相对于第l帧)
* @param[in] l 第l帧
* @param[in] relative_R 当前帧到第l帧的旋转矩阵
* @param[in] relative_T 当前帧到第l帧的平移向量
* @param[in] sfm_f 所有特征点
* @param[out] sfm_tracked_points 所有在sfm中三角化的特征点ID和坐标
* @return bool true:sfm求解成功
*/
bool GlobalSFM::construct(int frame_num, Quaterniond* q, Vector3d* T, int l,
const Matrix3d relative_R, const Vector3d relative_T,
vector<SFMFeature> &sfm_f, map<int, Vector3d> &sfm_tracked_points)假设第l帧为原点,初始化第l帧(q[l]和T[l])和当前帧(q[frame_num-1]和T[frame_num-1])并赋值到Pose中
最后得到:Pose[i]的i是l 和 frame_num-1,第l帧和第frame_num-1帧的姿态初始化得到了。下一步可以先对这两帧三角化。
//假设第l帧为原点,根据当前帧到第l帧的relative_R,relative_T,得到当前帧位姿
q[l].w() = 1;// 第l帧
q[l].x() = 0;
q[l].y() = 0;
q[l].z() = 0;
T[l].setZero();
q[frame_num - 1] = q[l] * Quaterniond(relative_R);// 当前帧
T[frame_num - 1] = relative_T;
//cout << "init q_l " << q[l].w() << " " << q[l].vec().transpose() << endl;
//cout << "init t_l " << T[l].transpose() << endl;
//rotate to cam frame
Matrix3d c_Rotation[frame_num];// 旋转
Vector3d c_Translation[frame_num];// 平移
Quaterniond c_Quat[frame_num]; // 旋转四元数
double c_rotation[frame_num][4];
double c_translation[frame_num][3];
Eigen::Matrix<double, 3, 4> Pose[frame_num];// 位姿3*4,第l帧到每一帧变换矩阵
// 第l帧
c_Quat[l] = q[l].inverse();
c_Rotation[l] = c_Quat[l].toRotationMatrix();
c_Translation[l] = -1 * (c_Rotation[l] * T[l]);
Pose[l].block<3, 3>(0, 0) = c_Rotation[l];
Pose[l].block<3, 1>(0, 3) = c_Translation[l];
// 滑动窗最后一帧,即当前帧
c_Quat[frame_num - 1] = q[frame_num - 1].inverse();
c_Rotation[frame_num - 1] = c_Quat[frame_num - 1].toRotationMatrix();
c_Translation[frame_num - 1] = -1 * (c_Rotation[frame_num - 1] * T[frame_num - 1]);
Pose[frame_num - 1].block<3, 3>(0, 0) = c_Rotation[frame_num - 1];
Pose[frame_num - 1].block<3, 1>(0, 3) = c_Translation[frame_num - 1];
1)上部分初始化了第l帧和第frame_num-1帧的姿态,以第l帧的姿态作为世界坐标系,三角化 l 和framenum-1帧 。
2)再用pnp估计出下一帧的位姿,下一帧再与最后一帧三角定位估计更多三维点。三角化 l+1,l+2...frmaenum-2和framenum-1帧
3)从l帧开始往第一帧,逐渐帧pnp,再与第l帧进行三角定位得到更多的三维点。三角化 l-1, l-2, l-3, …, 0帧与 l 帧
每帧pnp时位姿初值都用的上一个关键帧的位姿。
4)剩下的没有三角化的特征点,通过它被观察的第一帧和最后一帧进行三角定位。
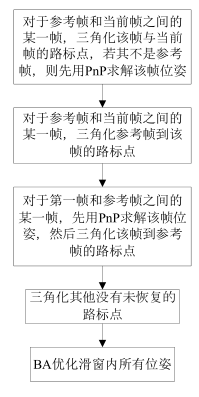
1)、pnp得到 l,l+1,l+2...frmaenum-2相机位姿,三角化l,l+1,l+2...frmaenum-2和framenum-1帧
for (int i = l; i < frame_num - 1 ; i++)
{
if (i > l)
{
Matrix3d R_initial = c_Rotation[i - 1];
Vector3d P_initial = c_Translation[i - 1];
// 求解PnP得到RT
if(!solveFrameByPnP(R_initial, P_initial, i, sfm_f))
return false;
c_Rotation[i] = R_initial;
c_Translation[i] = P_initial;
c_Quat[i] = c_Rotation[i];
Pose[i].block<3, 3>(0, 0) = c_Rotation[i];
Pose[i].block<3, 1>(0, 3) = c_Translation[i];
}
// l,l+1,l+2.....framenum-2和framenum-1 三角化恢复路标3D坐标
triangulateTwoFrames(i, Pose[i], frame_num - 1, Pose[frame_num - 1], sfm_f);
}这里其实是两部分,当i==l时,不进入if 语句,直接进行三角化triangulateTwoFrames。第l帧和第frame_num-1帧之间。
下一步i=l+1, l+2 ,l+3......都是先用solveFrameByPnP函数用PnP得到当前帧相机位姿,再三角化 triangulateTwoFrames
最终得到的是三角化l,l+1,l+2...frmaenum-2和framenum-1帧
后面会对三个函数solveFrameByPnP函数和triangulateTwoFrames()和triangulatePoint()进行详细讲解
都在initial_sfm.cpp中
solveFrameByPnP()函数得到第i帧的RT
/* @brief PNP方法得到第l帧到第i帧的位姿
* @param[in] i 第i帧
* @param[update] R_initial、P_initial、sfm_f
*/
bool GlobalSFM::solveFrameByPnP(Matrix3d &R_initial, Vector3d &P_initial, int i,
vector<SFMFeature> &sfm_f)
{
vector<cv::Point2f> pts_2_vector;
vector<cv::Point3f> pts_3_vector;
// 遍历所有特征点
for (int j = 0; j < feature_num; j++)
{
if (sfm_f[j].state != true)// 检查状态,该点是否被三角化
continue;
Vector2d point2d;
for (int k = 0; k < (int)sfm_f[j].observation.size(); k++)
{
if (sfm_f[j].observation[k].first == i)// 判断图像帧索引是否相同
{
// 通过观测得到2D像素点
Vector2d img_pts = sfm_f[j].observation[k].second;
cv::Point2f pts_2(img_pts(0), img_pts(1));
pts_2_vector.push_back(pts_2);
// 通过position得到路标3D坐标
cv::Point3f pts_3(sfm_f[j].position[0], sfm_f[j].position[1], sfm_f[j].position[2]);
pts_3_vector.push_back(pts_3);
break;
}
}
}
if (int(pts_2_vector.size()) < 15)// 判断像素点数量是否足够
{
printf("unstable features tracking, please slowly move you device!n");
if (int(pts_2_vector.size()) < 10)
return false;
}
cv::Mat r, rvec, t, D, tmp_r;
cv::eigen2cv(R_initial, tmp_r);
cv::Rodrigues(tmp_r, rvec);
cv::eigen2cv(P_initial, t);
cv::Mat K = (cv::Mat_<double>(3, 3) << 1, 0, 0, 0, 1, 0, 0, 0, 1);
bool pnp_succ;
pnp_succ = cv::solvePnP(pts_3_vector, pts_2_vector, K, D, rvec, t, 1);
if(!pnp_succ)
{
return false;
}
cv::Rodrigues(rvec, r);
//cout << "r " << endl << r << endl;
MatrixXd R_pnp;
cv::cv2eigen(r, R_pnp);
MatrixXd T_pnp;
cv::cv2eigen(t, T_pnp);
R_initial = R_pnp;
P_initial = T_pnp;
return true;
}triangulateTwoFrames()函数三角化两帧特征点,更新sfm_f.position
/* @brief 三角化frame0和frame1间所有对应点
* @param[in] frame,Pose 帧索引和位姿数据
* @param[out] sfm_f的state和position 3D坐标
*/
//
void GlobalSFM::triangulateTwoFrames(int frame0, Eigen::Matrix<double, 3, 4> &Pose0,
int frame1, Eigen::Matrix<double, 3, 4> &Pose1,
vector<SFMFeature> &sfm_f)
{
assert(frame0 != frame1);
for (int j = 0; j < feature_num; j++)// 遍历所有特征点
{
if (sfm_f[j].state == true) // 没有三角化的话才开始三角化
continue;
//
bool has_0 = false, has_1 = false;
Vector2d point0; Vector2d point1;
for (int k = 0; k < (int)sfm_f[j].observation.size(); k++)
{ // 找到对应的帧索引,取出2D像素坐标
if (sfm_f[j].observation[k].first == frame0)
{
point0 = sfm_f[j].observation[k].second;
has_0 = true;
}
if (sfm_f[j].observation[k].first == frame1)
{
point1 = sfm_f[j].observation[k].second;
has_1 = true;
}
}
// 如果2D像素坐标都匹配上了,三角化
if (has_0 && has_1)
{
Vector3d point_3d;
triangulatePoint(Pose0, Pose1, point0, point1, point_3d);
sfm_f[j].state = true; // 实现三角化了
sfm_f[j].position[0] = point_3d(0);
sfm_f[j].position[1] = point_3d(1);
sfm_f[j].position[2] = point_3d(2);
//cout << "trangulated : " << frame1 << " 3d point : " << j << " " << point_3d.transpose() << endl;
}
}
}线性三角化法DLT triangulatePoint()已知两帧对应的2D点和两帧的相机位姿,求解路标3D坐标。
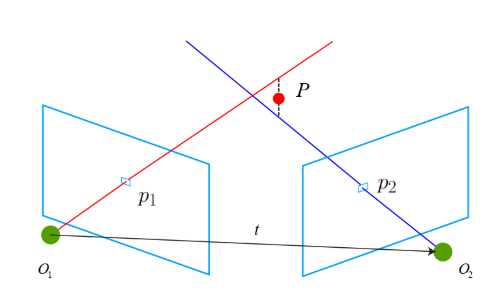
路标点P(XYZ),在两帧上成像为 x1(u1,v1)和 x2(u2,v2),外参矩阵分别为P1和P2,
二者变换方程:
两边同时乘以x1的反对称矩阵,可得:![]()
这里的T不是转置矩阵,是反对称矩阵的意思。
第三个式子是前两个式子相减得到,每对特征点可以做成两个式子,最少需要两对特征点才能解。
两个特征点各自取两个方程,组成 AX=0
/* @brief 三角化两帧间某个对应特征点的深度
* @param[in] Pose和point
* @param[out] point_3d
*/
void GlobalSFM::triangulatePoint(Eigen::Matrix<double, 3, 4> &Pose0, Eigen::Matrix<double, 3, 4> &Pose1,
Vector2d &point0, Vector2d &point1, Vector3d &point_3d)
{
Matrix4d design_matrix = Matrix4d::Zero();
design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);
design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);
design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);
design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);
Vector4d triangulated_point;
triangulated_point =
design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();
point_3d(0) = triangulated_point(0) / triangulated_point(3);
point_3d(1) = triangulated_point(1) / triangulated_point(3);
point_3d(2) = triangulated_point(2) / triangulated_point(3);
}2)、三角化 l+1,l+2......framenum-2和 l 帧
for (int i = l + 1; i < frame_num - 1; i++)
triangulateTwoFrames(l, Pose[l], i, Pose[i], sfm_f);3)、pnp得到l-1,l-2.....0相机位姿,三角化 l-1, l-2, l-3, …, 0帧与l帧
for (int i = l - 1; i >= 0; i--)
{
//solve pnp
Matrix3d R_initial = c_Rotation[i + 1];
Vector3d P_initial = c_Translation[i + 1];
if(!solveFrameByPnP(R_initial, P_initial, i, sfm_f))
return false;
c_Rotation[i] = R_initial;
c_Translation[i] = P_initial;
c_Quat[i] = c_Rotation[i];
Pose[i].block<3, 3>(0, 0) = c_Rotation[i];
Pose[i].block<3, 1>(0, 3) = c_Translation[i];
//triangulate
triangulateTwoFrames(i, Pose[i], l, Pose[l], sfm_f);
}4)、剩下的没有三角化的特征点,通过它被观察的第一帧和最后一帧进行三角定位。
// 5、三角化其他未恢复的特征点,即sfm_f[j].state==false的点
// 选择它被观测到的第一帧和最后一帧进行三角定位
// 至此得到了滑动窗口中所有图像帧的位姿以及特征点的3d坐标
for (int j = 0; j < feature_num; j++)
{
if (sfm_f[j].state == true)
continue;
if ((int)sfm_f[j].observation.size() >= 2)
{
Vector2d point0, point1;
int frame_0 = sfm_f[j].observation[0].first;// 第一帧
point0 = sfm_f[j].observation[0].second;
int frame_1 = sfm_f[j].observation.back().first;// 最后一帧
point1 = sfm_f[j].observation.back().second;
Vector3d point_3d;
triangulatePoint(Pose[frame_0], Pose[frame_1], point0, point1, point_3d);
sfm_f[j].state = true;
sfm_f[j].position[0] = point_3d(0);
sfm_f[j].position[1] = point_3d(1);
sfm_f[j].position[2] = point_3d(2);
//cout << "trangulated : " << frame_0 << " " << frame_1 << " 3d point : " << j << " " << point_3d.transpose() << endl;
}
}
5)、使用cares进行全局BA优化(相机位姿和特征点坐标)
固定住l帧的位置和姿态,固定住最后一帧的位置。因为这时候的图像位姿和点的位置都不太准,所以用ceres统一一起优化图像位姿和三维点位置,优化重投影误差。优化的测量值是,特征点在每帧中被观察到的位置,可以转成重投影误差约束。有关的自变量是,每帧图像的位姿,特征点的三维坐标。
优化完成之后,即用ceres优化出这些关键帧的位姿和地图点后,再用pnp算出在这段时间区域内的所有图像的位姿。每个图像的计算都用下一个关键帧的位姿来当pnp的初值
ceres::Problem problem;
ceres::LocalParameterization* local_parameterization = new ceres::QuaternionParameterization();
//cout << " begin full BA " << endl;
for (int i = 0; i < frame_num; i++)
{
//double array for ceres
c_translation[i][0] = c_Translation[i].x();
c_translation[i][1] = c_Translation[i].y();
c_translation[i][2] = c_Translation[i].z();
c_rotation[i][0] = c_Quat[i].w();
c_rotation[i][1] = c_Quat[i].x();
c_rotation[i][2] = c_Quat[i].y();
c_rotation[i][3] = c_Quat[i].z();
problem.AddParameterBlock(c_rotation[i], 4, local_parameterization);
problem.AddParameterBlock(c_translation[i], 3);
if (i == l)
{
problem.SetParameterBlockConstant(c_rotation[i]);
}
if (i == l || i == frame_num - 1)
{
problem.SetParameterBlockConstant(c_translation[i]);
}
}
for (int i = 0; i < feature_num; i++)
{
if (sfm_f[i].state != true)
continue;
for (int j = 0; j < int(sfm_f[i].observation.size()); j++)
{
int l = sfm_f[i].observation[j].first;
ceres::CostFunction* cost_function = ReprojectionError3D::Create(
sfm_f[i].observation[j].second.x(),
sfm_f[i].observation[j].second.y());
problem.AddResidualBlock(cost_function, NULL, c_rotation[l], c_translation[l],
sfm_f[i].position);
}
}
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_SCHUR;
//options.minimizer_progress_to_stdout = true;
options.max_solver_time_in_seconds = 0.2;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
//std::cout << summary.BriefReport() << "n";
if (summary.termination_type == ceres::CONVERGENCE || summary.final_cost < 5e-03)
{
//cout << "vision only BA converge" << endl;
}
else
{
//cout << "vision only BA not converge " << endl;
return false;
}
//这里得到的是第l帧坐标系到各帧的变换矩阵,应将其转变为各帧在第l帧坐标系上的位姿
for (int i = 0; i < frame_num; i++)
{
q[i].w() = c_rotation[i][0];
q[i].x() = c_rotation[i][1];
q[i].y() = c_rotation[i][2];
q[i].z() = c_rotation[i][3];
q[i] = q[i].inverse();
//cout << "final q" << " i " << i <<" " <<q[i].w() << " " << q[i].vec().transpose() << endl;
}
for (int i = 0; i < frame_num; i++)
{
T[i] = -1 * (q[i] * Vector3d(c_translation[i][0], c_translation[i][1], c_translation[i][2]));
//cout << "final t" << " i " << i <<" " << T[i](0) <<" "<< T[i](1) <<" "<< T[i](2) << endl;
}
for (int i = 0; i < (int)sfm_f.size(); i++)
{
if(sfm_f[i].state)
sfm_tracked_points[sfm_f[i].id] = Vector3d(sfm_f[i].position[0], sfm_f[i].position[1], sfm_f[i].position[2]);
}
return true;
}以上是对sfm.construct()函数进行了详细解读,第一部分纯视觉SFM结束,需要强调的是这里的Q、T存储的是每一帧相对于第l帧(参考帧)的相对位姿。
前面只得到了滑动窗口内所有关键帧的位姿,但由于并不是第一次视觉初始化就能成功,此时图像帧数目有可能会超过滑动窗口的大小。此时要对那些不被包括在滑动窗口内的图像帧位姿进行求解。
solve pnp for all frame
5、对于所有的图像帧,包括不在滑动窗口中的,提供初始的RT估计
//5. 对于所有的图像帧,包括不在滑动窗口中的,提供初始的RT估计,然后solvePnP进行优化,得到每一帧的姿态
map<double, ImageFrame>::iterator frame_it;
map<int, Vector3d>::iterator it;
frame_it = all_image_frame.begin( );
for (int i = 0; frame_it != all_image_frame.end( ); frame_it++)
{
cv::Mat r, rvec, t, D, tmp_r;
// 初始化估计值
if((frame_it->first) == Headers[i].stamp.toSec())
{
frame_it->second.is_key_frame = true;
frame_it->second.R = Q[i].toRotationMatrix() * RIC[0].transpose();
frame_it->second.T = T[i];
i++;
continue;
}
if((frame_it->first) > Headers[i].stamp.toSec())
{
i++;
}
// Q和T是图像帧的位姿,而不是求解PNP时所用的坐标系变换矩阵
Matrix3d R_inital = (Q[i].inverse()).toRotationMatrix();
Vector3d P_inital = - R_inital * T[i];
cv::eigen2cv(R_inital, tmp_r);
//罗德里格斯公式将旋转矩阵转换成旋转向量
cv::Rodrigues(tmp_r, rvec);
cv::eigen2cv(P_inital, t);
frame_it->second.is_key_frame = false;
vector<cv::Point3f> pts_3_vector; // 3D坐标
vector<cv::Point2f> pts_2_vector; // 2D坐标
for (auto &id_pts : frame_it->second.points)
{
int feature_id = id_pts.first;// 特征点索引
for (auto &i_p : id_pts.second)
{
it = sfm_tracked_points.find(feature_id);
// 出现过,否则it就等于.end()了
if(it != sfm_tracked_points.end())
{
//
Vector3d world_pts = it->second;
cv::Point3f pts_3(world_pts(0), world_pts(1), world_pts(2));
pts_3_vector.push_back(pts_3);
Vector2d img_pts = i_p.second.head<2>();
cv::Point2f pts_2(img_pts(0), img_pts(1));
pts_2_vector.push_back(pts_2);
}
}
}
//保证特征点数大于5
cv::Mat K = (cv::Mat_<double>(3, 3) << 1, 0, 0, 0, 1, 0, 0, 0, 1);
if(pts_3_vector.size() < 6)
{
cout << "pts_3_vector size " << pts_3_vector.size() << endl;
ROS_DEBUG("Not enough points for solve pnp !");
return false;
}
/**
*bool cv::solvePnP( 求解pnp问题
* InputArray objectPoints, 特征点的3D坐标数组
* InputArray imagePoints, 特征点对应的图像坐标
* InputArray cameraMatrix, 相机内参矩阵
* InputArray distCoeffs, 失真系数的输入向量
* OutputArray rvec, 旋转向量
* OutputArray tvec, 平移向量
* bool useExtrinsicGuess = false, 为真则使用提供的初始估计值
* int flags = SOLVEPNP_ITERATIVE 采用LM优化
*)
*/
if (! cv::solvePnP(pts_3_vector, pts_2_vector, K, D, rvec, t, 1))
{
ROS_DEBUG("solve pnp fail!");
return false;
}
cv::Rodrigues(rvec, r);
MatrixXd R_pnp,tmp_R_pnp;
cv::cv2eigen(r, tmp_R_pnp);
//这里也同样需要将坐标变换矩阵转变成图像帧位姿,并转换为IMU坐标系的位姿
R_pnp = tmp_R_pnp.transpose();
MatrixXd T_pnp;
cv::cv2eigen(t, T_pnp);
T_pnp = R_pnp * (-T_pnp);
frame_it->second.R = R_pnp * RIC[0].transpose();
frame_it->second.T = T_pnp;
}6、进行视觉惯性联合初始化
if (visualInitialAlign())
return true;
else
{
ROS_INFO("misalign visual structure with IMU");
return false;
}最后
以上就是懦弱荷花最近收集整理的关于VINS-Mono 代码详细解读——初始化1:视觉SFM详解 processImage()+initialStructure()Estimator类 processImage()函数的全部内容,更多相关VINS-Mono内容请搜索靠谱客的其他文章。








发表评论 取消回复