初始化大致流程
- 如果IMU和相机之间的外参未知,则需要在线标定求解旋转量qbc。
- 利用求解出来的qbc,结合相机间的约束,求解IMU角速度的bias。
- 利用IMU的运动估计重力,速度以及尺度。
- 利用重力的模长矫正重力,之后再矫正每个参数。
1.估计外参qbc
根据相机和IMU的坐标相对关系可得
![]()
整理得:
![]()
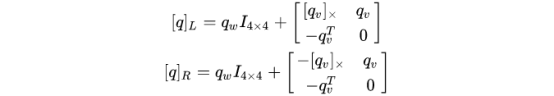
将多个帧之间的等式关系一起构建超定方程Ax=0,如下:
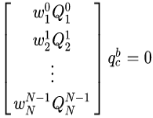
对A进行svd分解,其中最小奇异值对应的奇异向量便为需要求解的qbc。
其中
![]()
由于旋转矩阵和欧拉角之间的关系公式如下:
![]()
可以求解出r
![]()
在此没有估计平移外参, 因为默认为该外参对系统的影响是线性的, 可以通过离线标定, 出场设定或者尺子测量得出。在VINS-Mono中如果设定要标定外参, 但该平移外参也会在初始化阶段最后的Full BA优化中进行优化。
2.求解bg
由于现在还不知道世界帧的任何信息,本文将第一个相机帧作为SFM的参考帧。所有帧的位姿和特征点位置是相对于第0帧的相机。假设已经有了关于相机和IMU之间的测量外参数,可以将位姿从相机坐标系转换为(IMU)坐标系(有旋转约束和平移约束):
这一部分和基于图像的三维重建比较像,可以用三角化和PnP把这一串的ck帧的位姿和特征点位置确定下来(特征点是伪深度),在加上外参数qbc和pbc,一系列bk帧的位姿也确定下来。注意,这里把c0帧作为基础帧,实际上,c0帧旋转一下使gc0和gw方向一致时获得的坐标系就是vins的世界坐标系,也就是先验。
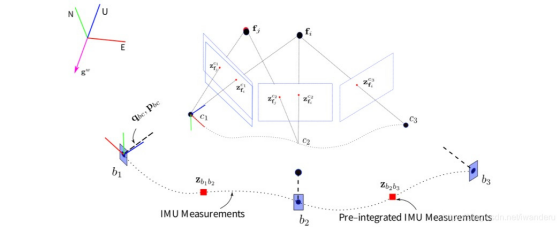
如上图所示,说明:图中位姿(Rc0ck,qc0ck)表示的是相对于第一帧相机坐标系(·)c0。相机到IMU的外参为(Rbc,qbc),得到姿态从相机坐标系转换到IMU坐标系的关系。
![]()
![]()
![]()
![]()
建立求解bg的目标函数如下
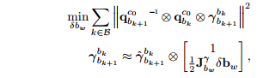
![]() 是相机在bk到bk+1的相对旋转,
是相机在bk到bk+1的相对旋转,![]() 是陀螺仪从bk到bk+1的旋转量,第二个式子给出了
是陀螺仪从bk到bk+1的旋转量,第二个式子给出了![]() 对陀螺仪偏置的一阶泰勒展开。
对陀螺仪偏置的一阶泰勒展开。
根据目标方程中的关系,理论上该方程的值是为单位四元数,但是因为![]() 存在偏置,因此会出现误差,一般均采用最小二乘求解,具体推导如下:
存在偏置,因此会出现误差,一般均采用最小二乘求解,具体推导如下:
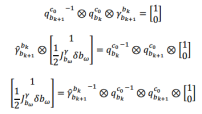
![]()
由于在在sfm完成且外参数标定完之后,![]() 两个值是已知的了,
两个值是已知的了,![]() 通过IMU预积分求得,
通过IMU预积分求得,![]() 也已知,所以可以通过最小化这个目标函数的,可以把旋转bias求解!其实VINS-mono这里不像那种用高斯牛顿法迭求解,而更像是用直接法,也就是矩阵运算的方式来求待优化的状态量(使用LDLT求解)。在得到陀螺仪偏置之后,重新对IMU预积分
也已知,所以可以通过最小化这个目标函数的,可以把旋转bias求解!其实VINS-mono这里不像那种用高斯牛顿法迭求解,而更像是用直接法,也就是矩阵运算的方式来求待优化的状态量(使用LDLT求解)。在得到陀螺仪偏置之后,重新对IMU预积分![]() 进行估计。
进行估计。
3.速度、重力和米制尺度初始化
在估计完陀螺仪偏置之后需要估计速度,重力和尺度因子,其状态量可以写成以下形式:
![]()
其中, ![]() 表示第k时刻的body坐标系下速度在取第k帧图像的时候,
表示第k时刻的body坐标系下速度在取第k帧图像的时候, ![]() 表示重力向量在第0帧相机坐标系下的表示。s表示尺度因子,将视觉轨迹拉伸到米制单位。在世界坐标系下的有:
表示重力向量在第0帧相机坐标系下的表示。s表示尺度因子,将视觉轨迹拉伸到米制单位。在世界坐标系下的有:
我们通过IMU预积分可得:
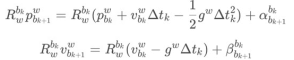
整理可得
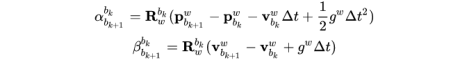
但是世界坐标系我们不知道,只知道c0坐标系,所以需要把上面的公式转到c0坐标系上:
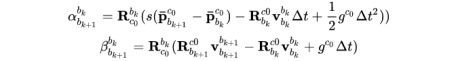
将上式展开,并将第2节中的公式带入,得到:
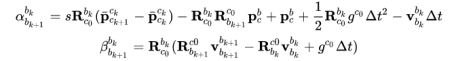
将需要优化的量放在右边,与优化无关的量放在左边,得到:
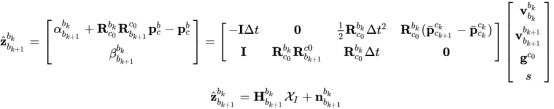
在上式中 ![]() 都可以从SFM中获得,
都可以从SFM中获得, ![]() 是两个图像帧之间的时间间隔,通过最小二乘法使下式最小化,就可以估计出速度,重力和尺度。
是两个图像帧之间的时间间隔,通过最小二乘法使下式最小化,就可以估计出速度,重力和尺度。
![]()
这里同样采用LDLT方法进行求解,并且用上了信息矩阵,这里通过该值的模长与实际重力大小9.81的误差是否大于0.5(也就是约5%的重力值),来判断此次初始化是否成功。
4.重力优化
需要对重力进行优化的原因主要是因为在之前的线性初始化过程中并没有对重力的幅度进行限制,所有重力只有两个自由度。在许多场合下,重力的幅度是已知的,因此可以重新参数化重力向量在切平面的两个变量,与重力正交的且在切平面上的两个向b1和b2如下图所示:
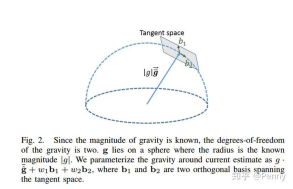
如上图,采用球面坐标进行参数化,也就是用g的模长作为半径画一个半球,上图蓝色线对应的是gc0的测量值的方向(也就是优化前的方向),在这个交点上找到一个切平面,用gc0,b1,b2构造一个坐标系,那么在轴b1和b2上坐标值w1和w2就是我们需要求的量。求出来之后,把等号右边加在一起,就是优化后的gc0值。

注意,b1的方向是由gc0的测量值的方向与[1,0,0]作叉乘得到的,b2的方向是由gc0的测量值的方向与b1作叉乘得到的。具体操作如上表所示,因此重力向量被改写为
![]()
将与之前求出的 ![]() 有关的变量移到方程的左边,再一次对
有关的变量移到方程的左边,再一次对![]() 进行优化,将优化得到的结果相加(由于w只有两个值所以只需要2个变量)。它的左边项也发生了改变,变成了:
进行优化,将优化得到的结果相加(由于w只有两个值所以只需要2个变量)。它的左边项也发生了改变,变成了:
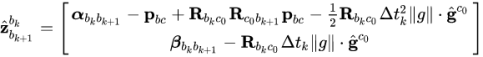
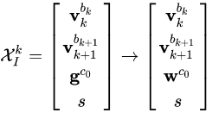
优化参数少了一个,因为多另一个模值的信息,Hessian矩阵对于重力优化的部分会乘以[w1, w2],这是个3*2的矩阵,所以优化变量就少了一个。在这里同样采用LDLT分解求解。
重力优化后得到了在窗口中的第一帧的图像坐标系下的重力,之后就可以通过世界坐标系下的重力加速度和相机坐标系下的重力加速度之间的关系求解出世界坐标系与相机坐标系之间的旋转矩阵。通过 ![]() 与
与![]() 之间的叉乘可以得到两者的旋转轴,再除以两者叉乘的模长就能得到他们的单位旋转轴,他们的旋转角可以通过如下计算:
之间的叉乘可以得到两者的旋转轴,再除以两者叉乘的模长就能得到他们的单位旋转轴,他们的旋转角可以通过如下计算:
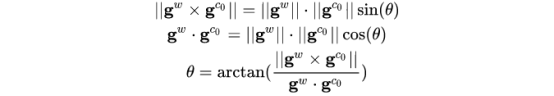
通过求解的角度可得![]() ;在代码中,得到该旋转矩阵之后,可以将第一帧图像坐标系下的所有变量都转换为世界坐标系下的值,在窗口中的所有帧都设置成了关键帧。至此,完成了初始化。
;在代码中,得到该旋转矩阵之后,可以将第一帧图像坐标系下的所有变量都转换为世界坐标系下的值,在窗口中的所有帧都设置成了关键帧。至此,完成了初始化。
最后
以上就是耍酷灰狼最近收集整理的关于VINS-mono初始化的原理解析的全部内容,更多相关VINS-mono初始化内容请搜索靠谱客的其他文章。








发表评论 取消回复