概述
估计器初始化
- 初始化的原因是单目惯性紧耦合系统是一个非线性程度很高的系统，首先单目是无法获得空间中的绝对尺度，而IMU又必然存在偏置，在后面进行求解的时候还需要用到重力加速度（包括大小和方向），对于速度比较敏感的条件下，比如说无人机，又要精确的速度信息，因此，如何有效的在紧耦合系统处理之前计算出这些量，对整个紧耦合系统的鲁棒性有着重大的意义
- 初始化要做的事其实说起来很简单，就是计算出绝对尺度s、陀螺仪偏置bg、加速度偏置ba、重力加速度G和每个IMU时刻的速度v
- VINS-Mono 的初始化采用松组合（loosely coupled）的方式获取初始值。 首先用 SFM求解滑动窗口内所有帧的位姿（以第一帧作为参考坐标系）和所有路标点的 3D 位置。然后将 SFM 的结果与 IMU 预积分的值进行对齐，实现对陀螺仪偏置的校正，再求解每一帧对应的速度，求解重力向量方向，恢复单目相机的尺度因子。
- 需要注意的是，在初始化过程中，并没有对加速度计的偏置进行校正，这是因为重力是初始化过程中待求的量，而加速度计偏置与重力耦合，而且系统的加速度相对于重力加速度很小，所以加速度计偏置在初始化过程中很难观测，因此初始化过程中不考虑加速度计偏置的校正。
滑动窗口(Sliding Window)纯视觉SfM
首先，我们检查了最新帧与之前所有帧之间的特征对应。如果我们能在滑动窗口中的最新帧和任何其他帧之间，找到稳定的特征跟踪(超过30个跟踪特征)和足够的视差(超过20个的旋转补偿像素)，使用五点法恢复这两个帧之间的相对旋转和尺度平移。否则，将最新的帧保存在窗口中，并等待新的帧。如果五点算法成功的话，任意设置尺度，并对这两个帧中观察到的所有特征进行三角化。基于这些三角特征，采用PnP来估计窗口中所有其他帧的姿态。最后，应用全局光束平差法(BA)最小化所有特征观测的重投影误差。由于我们还没有任何世界坐标系的知识，我们将第一个相机坐标系 ( ⋅ ) c 0 (·)^{c_0} (⋅)c0设置为SfM的参考坐标系。所有帧的位姿 ( p ˉ c k c 0 ， q c k c 0 ) (bar p^{c0}_{c_k}，q^{c0}_{c_k}) (pˉckc0，qckc0)和特征位置表示相对于 ( ⋅ ) c 0 (·)^{c_0} (⋅)c0。假设摄像机和IMU之间有一个粗略测量的外部参数 ( p c b , q c b ) (p^b_c,q^b_c) (pcb,qcb)，我们可以将姿态从相机坐标系转换到物体(IMU)坐标系。
纯视觉初始化时，我们采用第一帧 c0 作为基准坐标系，若要转化为从 body 坐标系到 c0坐标系，可以进行如下变换，其中s是匹配视觉结构与距离尺度的尺度参数，解出尺度参数是实现成功初始化的关键。
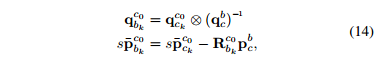
上式推导如下：
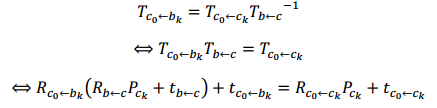
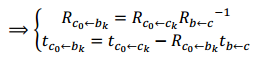
B. 视觉惯性校准（Visual-Inertial Alignment)
陀螺仪偏置标定
这 一 部 分 的 内 容 对 应 于 VINS-Mono 代 码 initial_aligment.cpp 中 的
solveGyroscopeBias()函数。
考虑滑动窗口中连续两帧
b
k
b_k
bk和
b
k
+
1
b_{k+1}
bk+1，我们从视觉sfM中得到旋转
q
b
k
c
0
q^{c0}_{b_k}
qbkc0和
q
b
k
+
1
c
0
q^{c0}_{b_{k+1}}
qbk+1c0，从IMU预积分得到的相对约束
γ
b
k
+
1
b
k
γ^{b_k}_{b_{k+1}}
γbk+1bk。
陀螺仪的误差有两部分测量噪声和陀螺仪偏置，噪声暂时可以忽略（毕竟太小），而视觉的误差就只有观测噪声（也可以忽略不管），因此两者差值的绝对值就是陀螺仪偏置，将整个滑动窗口的所有的旋转做差构成了一个最小化误差模型：
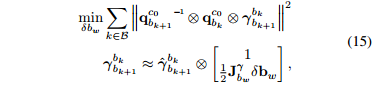
其中B代表窗口的所有帧。
q
b
k
c
0
q^{c0}_{b_k}
qbkc0
q
b
k
+
1
c
0
q^{c0}_{b_{k+1}}
qbk+1c0：相机从
b
k
b_k
bk到
b
k
+
1
b_{k+1}
bk+1下的相对旋转
γ
b
k
+
1
b
k
γ^{b_k}_{b_{k+1}}
γbk+1bk：陀螺仪从
b
k
+
1
b_{k+1}
bk+1到
b
k
b_k
bk下的相对旋转
第二个式子给出了
γ
b
k
+
1
b
k
γ^{b_k}_{b_{k+1}}
γbk+1bk对陀螺仪偏置的一阶近似。
因为四元数最小值为单位四元数 [1; 0v]T，所以
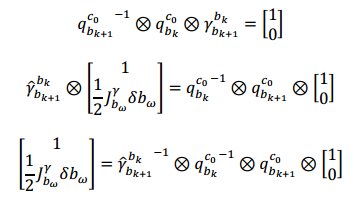
只考虑虚部，则有：
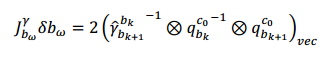
然后取最小二乘，当然也可以使用SVD分解等方法求解，得到了陀螺仪偏置 b w b_w bw的初始校准。然后我们用新的陀螺仪偏置重新传递所有的IMU预积分项 α ^ b k + 1 b k 、 β ^ b k + 1 b k 、 γ ^ b k + 1 b k hat α^{b_k}_{b_{k+1}}、hat β^{b_k}_{b_{k+1}}、hat γ^{b_k}_{b_{k+1}} α^bk+1bk、β^bk+1bk、γ^bk+1bk 。
速度、重力向量和尺度初始化：
这一部分的内容对应于 VINS-Mono 代码 initial_aligment.cpp 中的 LinearAlignment()
函数
在陀螺仪偏置初始化后，我们继续初始化导航的其他基本状态，即速度、重力向量和尺度：
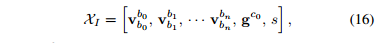
其中，
v
b
k
b
k
v^{b_k}_{b_k}
vbkbk是第k帧图像本体坐标系的速度，
g
c
0
g^{c_0}
gc0是
c
0
c_0
c0坐标系中的重力向量，s是单目SfM到公制单位的尺度。
在
c
0
c_0
c0坐标系的预积分：
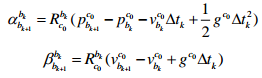
p
b
k
+
1
c
0
p^{c_0}_{b_{k+1}}
pbk+1c0和
p
b
k
c
0
p^{c_0}_{b_{k}}
pbkc0可由视觉 SFM 获得：
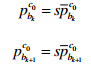
将此式带入上式得：
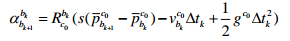
将等式中速度都转换到
c
0
c_0
c0 坐标系下：
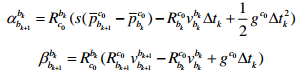
将上式转换成
H
x
=
b
Hx=b
Hx=b 的形式，这样便于利用 cholesky 进行求解，由
s
p
ˉ
b
k
c
0
=
p
c
k
c
0
−
R
c
k
c
0
p
c
b
sbar p^{c_0}_{b_k}=p^{c_0}_{c_k}-R^{c_0}_{c_k}p_c^b
spˉbkc0=pckc0−Rckc0pcb，带入上式得：
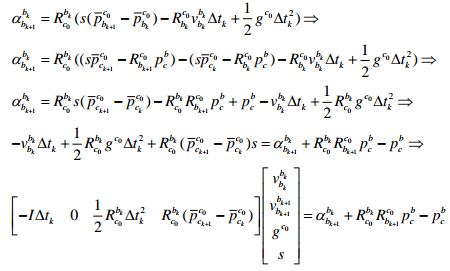
联力等式：
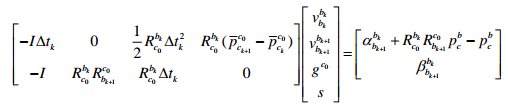
即：
H
6
×
10
X
I
10
×
1
=
b
6
×
1
H^{6×10}X_I^{ 10×1} = b^{6×1}
H6×10XI 10×1=b6×1
H矩阵一定是一个正定对称矩阵，以采用快速的 Cholosky 分解下面方程求解
X
I
X_I
XI：
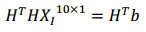
可以得到滑动窗口中所有关键帧的本体坐标系速度，视觉参照系
(
⋅
)
c
0
(·)^{c_0}
(⋅)c0的重力向量，以及单目尺度因子 s 。
修正重力矢量
这里计算的重力吸收了重力加速度计的偏置，虽然不需要计算重力加速度计的偏置，但重力还是需要优化的，说到优化重力加速度，肯定包含两个量，大小和方向，也就是三个维度，但是一般来说大小是确定已知的（这里设为9.8），因此其实我们要做的就是优化方向，是一个两维的向量，下图是优化重力的方法以及b1,b2单位向量的方向确定模型。
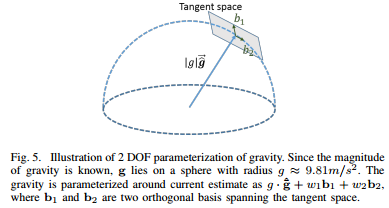将重力向量重新参数化：
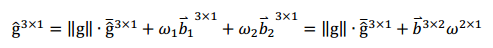
其中g是已知的重力大小，
g
^
ˉ
bar {hat g}
g^ˉ是表示重力方向的单位向量，b1、 b2为重力向量正切空间的一对
正交基 ，如图所示，w1和w2分别是在b1和b2上的对应位移。
将上式代入前面式子中，重新整理可得：
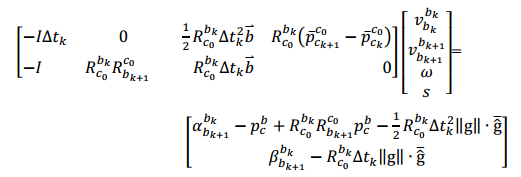
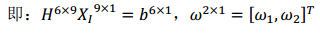
这样，可以用 Cholosky 分解下面方程求解
X
I
X_I
XI：
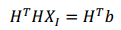
完成初始化：经过对重力向量的细化，通过将重力旋转到z轴上，得到世界坐标系与摄像机坐标系c0之间的旋转 q c 0 w q^w_{c_0} qc0w。然后我们将所有变量从参考坐标系 ( ⋅ ) c 0 (·)^{c_0} (⋅)c0 旋转到世界坐标系 ( ⋅ ) w (·)^w (⋅)w。本体坐标系的速度也将被旋转到世界坐标系。视觉SfM的变换矩阵将被缩放到度量单位。此时，初始化过程已经完成，所有这些度量值都将被输入到一个紧耦合的单目VIO中。
代码解析
流程图
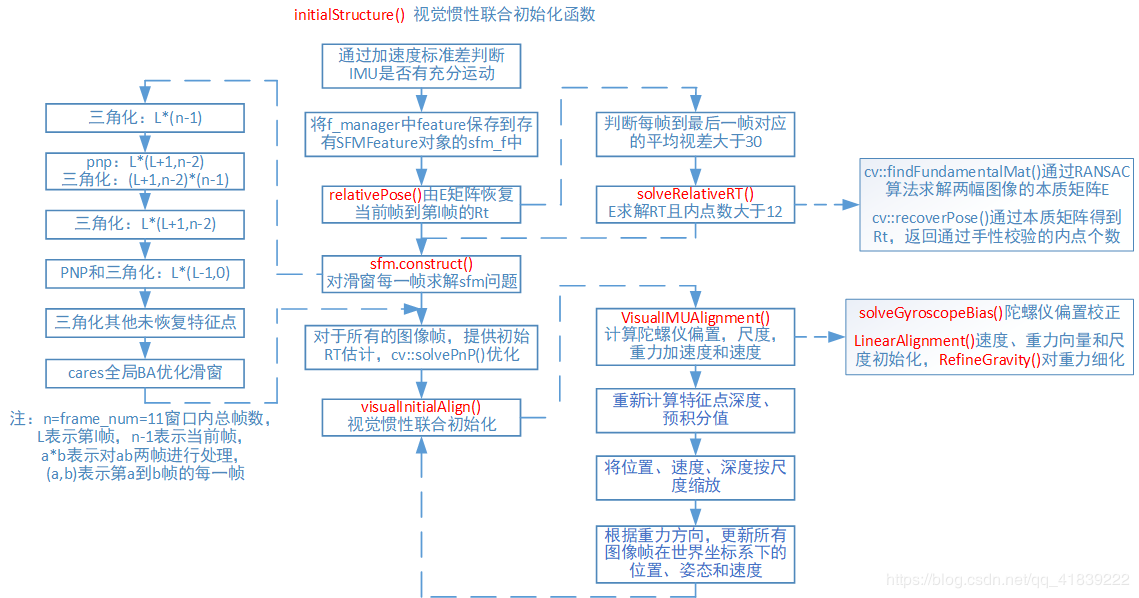
解析
直接从estimator.cpp中的 if (solver_flag == INITIAL) 开始
if (solver_flag == INITIAL) {
// 滑窗中的Keyframe达到指定大小的时候，才开始优化
if (frame_count == WINDOW_SIZE) {
bool result = false;
if (ESTIMATE_EXTRINSIC != 2 && (header.stamp.toSec() - initial_timestamp) > 0.1) {
result = initialStructure(); //! 初始化
initial_timestamp = header.stamp.toSec();
}
if (result) {
solver_flag = NON_LINEAR;
solveOdometry();
slideWindow();
f_manager.removeFailures();
ROS_INFO("Initialization finish!");
last_R = Rs[WINDOW_SIZE];
last_P = Ps[WINDOW_SIZE];
last_R0 = Rs[0];
last_P0 = Ps[0];
} else
slideWindow();
} else
frame_count++;
initialStructure() 视觉惯性联合初始化
- 1.通过计算线加速度的标准差，检测IMU的可观性，以进行初始化
注意这里并没有算上all_image_frame的第一帧，所以求均值和标准差的时候要减一
//! 通过计算预积分加速度的标准差，检测IMU的可观性
//check imu observibility
{
// 计算均值
map<double, ImageFrame>::iterator frame_it;
Vector3d sum_g;
for (frame_it = all_image_frame.begin(), frame_it++; frame_it != all_image_frame.end(); frame_it++)
{
double sum_dt = frame_it->second.pre_integration->sum_dt;
Vector3d tmp_g = frame_it->second.pre_integration->delta_v / sum_dt;
sum_g += tmp_g;
}
Vector3d aver_g = sum_g * 1.0 / ((int)all_image_frame.size() - 1);
// 计算方差
double var = 0;
for (frame_it = all_image_frame.begin(), frame_it++; frame_it != all_image_frame.end(); frame_it++)
{
double sum_dt = frame_it->second.pre_integration->sum_dt;
Vector3d tmp_g = frame_it->second.pre_integration->delta_v / sum_dt;
var += (tmp_g - aver_g).transpose() * (tmp_g - aver_g);
}
// 计算标准差
var = sqrt(var / ((int)all_image_frame.size() - 1));
//ROS_WARN("IMU variation %f!", var);
if(var < 0.25) //! 以标准差判断可观性
{
ROS_INFO("IMU excitation not enouth!");
//return false;
}
}
- 2.将f_manager中的所有feature保存到vector sfm_f中，SFMFeature数组中包含了特征点状态（是否被三角化），id，2d点，3d坐标以及深度，将特征管理器中的特征信息保存到SFMFeature对象sfm_f中sfm_f.push_back(tmp_feature)。
struct SFMFeature
{
bool state;//状态（是否被三角化）
int id;
vector<pair<int,Vector2d>> observation;//所有观测到该特征点的图像帧ID和图像坐标
double position[3];//3d坐标
double depth;//深度
};
// 遍历滑窗内所有的Features，以vector<SFMFeature>形式保存滑窗内所有特征点
vector<SFMFeature> sfm_f;
for (auto &it_per_id : f_manager.feature)
{
int imu_j = it_per_id.start_frame - 1;
SFMFeature tmp_feature;
tmp_feature.state = false;
tmp_feature.id = it_per_id.feature_id;
for (auto &it_per_frame : it_per_id.feature_per_frame)
{
imu_j++;
Vector3d pts_j = it_per_frame.point;
tmp_feature.observation.push_back(make_pair(imu_j, Eigen::Vector2d{pts_j.x(), pts_j.y()}));
}
sfm_f.push_back(tmp_feature);
}
-
3.relativePose()恢复出R、t
1.先通过 FeatureManager::getCorresponding()获取滑动窗口中第i帧和最后一帧的特征匹配corres
2.如果第i帧和最后一帧的特征匹配数corres大于20，且所有匹配的特征点的平均视差大于一定阈值，通过solveRelativeRT（定义在solv_5pts.cpp类中）用五点法求本质矩阵cv::findFundamentalMat 计算出当前帧到参考帧的 T值得注意：relativePose得到的位姿是第l帧的，第l帧的筛选是从第一帧开始到滑动窗口所有帧中一开始满足平均视差足够大的帧，这里的第l帧会作为参考帧到下面的全局SFM使用。这样得到图像的特征点2d坐标的提取，相机第l帧和最后一帧之间的旋转和平移
if (!relativePose(relative_R, relative_T, l)) { ROS_INFO("Not enough features or parallax; Move device around"); return false; }bool relativePose(relative_R, relative_T, l)
该函数判断每帧到窗口最后一帧对应特征点的平均视差大于30，且内点数目大于12则可进行初始化，同时返回当前帧到第l帧的坐标系变换R和T
bool Estimator::relativePose(Matrix3d &relative_R, Vector3d &relative_T, int &l) {
// find previous frame which contians enough correspondance and parallex with newest frame
// 在滑窗内寻找与最新的关键帧共视点超过20(像素点)的关键帧
for (int i = 0; i < WINDOW_SIZE; i++) {
vector<pair<Vector3d, Vector3d>> corres;
//获取第i帧和最后一帧的特征匹配corres
corres = f_manager.getCorresponding(i, WINDOW_SIZE);
// 共视的Features应该大于20
if (corres.size() > 20) {
// 求取匹配的特征点在图像上的视差和(归一化平面上)
double sum_parallax = 0;
for (int j = 0; j < int(corres.size()); j++) {
Vector2d pts_0(corres[j].first(0), corres[j].first(1));
Vector2d pts_1(corres[j].second(0), corres[j].second(1));
double parallax = (pts_0 - pts_1).norm();
sum_parallax = sum_parallax + parallax;
}
// 求取所有匹配的特征点的平均视差
double average_parallax = 1.0 * sum_parallax / int(corres.size());
// 视差大于一定阈值，并且能够有效地求解出变换矩阵
if (average_parallax * 460 > 30 && m_estimator.solveRelativeRT(corres, relative_R, relative_T)) {
l = i;
ROS_DEBUG("average_parallax %f choose l %d and newest frame to triangulate the whole structure",
average_parallax * 460, l);
return true;
}
}
}
return false;
}
FeatureManager::getCorresponding()
vector<pair<Vector3d, Vector3d>> FeatureManager::getCorresponding(int frame_count_l, int frame_count_r) {
vector<pair<Vector3d, Vector3d>> corres;
for (auto &it : feature) {
// 保证两帧的id大于当前特征点的起始id小于当前特征点的终止id
if (it.start_frame <= frame_count_l && it.endFrame() >= frame_count_r) {
int idx_l = frame_count_l - it.start_frame;
int idx_r = frame_count_r - it.start_frame;
Vector3d a = it.feature_per_frame[idx_l].point;
Vector3d b = it.feature_per_frame[idx_r].point;
corres.push_back(make_pair(a, b));
}
}
return corres;
}
solveRelativeRT()
bool MotionEstimator::solveRelativeRT(const vector<pair<Vector3d, Vector3d>> &corres, Matrix3d &Rotation, Vector3d &Translation)
{
if (corres.size() >= 15)
{
//! Step1：提取匹配完的Features
vector<cv::Point2f> ll, rr;
for (int i = 0; i < int(corres.size()); i++)
{
ll.push_back(cv::Point2f(corres[i].first(0), corres[i].first(1)));
rr.push_back(cv::Point2f(corres[i].second(0), corres[i].second(1)));
}
cv::Mat mask;
//! Step2：利用Ransac算法计算本质矩阵，内外点的阈值距离设定为0.3 / 460
cv::Mat E = cv::findFundamentalMat(ll, rr, cv::FM_RANSAC, 0.3 / 460, 0.99, mask);
cv::Mat cameraMatrix = (cv::Mat_<double>(3, 3) << 1, 0, 0, 0, 1, 0, 0, 0, 1);
//! Step3：计算变换矩阵并得到内点个数
cv::Mat rot, trans;
int inlier_cnt = cv::recoverPose(E, ll, rr, cameraMatrix, rot, trans, mask);
//cout << "inlier_cnt " << inlier_cnt << endl;
//! 得到变换矩阵 ll ==> rr
Eigen::Matrix3d R;
Eigen::Vector3d T;
for (int i = 0; i < 3; i++)
{
T(i) = trans.at<double>(i, 0);
for (int j = 0; j < 3; j++)
R(i, j) = rot.at<double>(i, j);
}
//! Step4：得到旋转矩阵和平移量 rr ==> ll
Rotation = R.transpose();
Translation = -R.transpose() * T;
//! 判断求取的内点个数是否满足要求
if(inlier_cnt > 12)
return true;
else
return false;
}
return false;
}
- 4.对窗口中每个图像帧求解sfm问题，调用sfm.construct(frame_count + 1, Q, T,l,relative_R, relative_T,sfm_f, sfm_tracked_points)估计slidingwindow中所有图像帧相对于参考帧（这里以第l帧作为参考帧）的旋转四元数Q、平移向量T和特征点坐标sfm_tracked_points。
// 三角化恢复滑窗内的Features
GlobalSFM sfm;
Quaterniond Q[frame_count + 1];
Vector3d T[frame_count + 1];
map<int, Vector3d> sfm_tracked_points;
if(!sfm.construct(frame_count + 1, Q, T, l, relative_R, relative_T, sfm_f, sfm_tracked_points))
{
ROS_DEBUG("global SFM failed!");
marginalization_flag = MARGIN_OLD;
return false;
}
bool GlobalSFM::construct()
函数位于inital_sfm.cpp文件中
纯视觉sfm，求解窗口中所有图像帧的位姿QT（相对于第l帧）和特征点坐标sfm_tracked_points
frame_num=frame_count + 1=11，frame_num-1表示当前帧
1.把第l帧看作参考坐标系，根据当前帧到第l帧的relative_R，relative_T，得到当前帧在参考坐标系下的位姿，之后的pose[i]表示第l帧到第i帧的变换矩阵[R|T]
2.三角化第l帧（参考帧）与第frame_num-1帧（当前帧）的路标点
3.pnp求解参考坐标系到第l+1开始的每一帧的变换矩阵R_initial, P_initial，保存在Pose中，并与当前帧进行三角化
4.对第l帧与从第l+1到frame_num-2的每一帧再进行三角化
5.PNP求解参考坐标系到从第l-1到第0帧的每一帧之间的变换矩阵，并进行三角化
6.三角化其他未恢复的特征点。至此得到了滑动窗口中所有图像帧的位姿以及特征点的3d坐标
7.使用cares进行全局BA优化
8.得到的是第l帧坐标系到各帧的变换矩阵，将其转变为每一帧在第l帧坐标系上的位姿
bool GlobalSFM::construct(int frame_num, Quaterniond* q, Vector3d* T, int l,
const Matrix3d relative_R, const Vector3d relative_T,
vector<SFMFeature> &sfm_f, map<int, Vector3d> &sfm_tracked_points)
{
feature_num = sfm_f.size();
//cout << "set 0 and " << l << " as known " << endl;
// have relative_r relative_t
// intial two view
q[l].w() = 1;
q[l].x() = 0;
q[l].y() = 0;
q[l].z() = 0;
T[l].setZero();
q[frame_num - 1] = q[l] * Quaterniond(relative_R);
T[frame_num - 1] = relative_T;
//cout << "init q_l " << q[l].w() << " " << q[l].vec().transpose() << endl;
//cout << "init t_l " << T[l].transpose() << endl;
//rotate to cam frame
Matrix3d c_Rotation[frame_num];
Vector3d c_Translation[frame_num];
Quaterniond c_Quat[frame_num];
double c_rotation[frame_num][4];
double c_translation[frame_num][3];
Eigen::Matrix<double, 3, 4> Pose[frame_num];
c_Quat[l] = q[l].inverse();
c_Rotation[l] = c_Quat[l].toRotationMatrix();
c_Translation[l] = -1 * (c_Rotation[l] * T[l]);
Pose[l].block<3, 3>(0, 0) = c_Rotation[l];
Pose[l].block<3, 1>(0, 3) = c_Translation[l];
c_Quat[frame_num - 1] = q[frame_num - 1].inverse();
c_Rotation[frame_num - 1] = c_Quat[frame_num - 1].toRotationMatrix();
c_Translation[frame_num - 1] = -1 * (c_Rotation[frame_num - 1] * T[frame_num - 1]);
Pose[frame_num - 1].block<3, 3>(0, 0) = c_Rotation[frame_num - 1];
Pose[frame_num - 1].block<3, 1>(0, 3) = c_Translation[frame_num - 1];
//1: trangulate between l ----- frame_num - 1
//2: solve pnp l + 1; trangulate l + 1 ------- frame_num - 1;
for (int i = l; i < frame_num - 1 ; i++)
{
// solve pnp
//pnp求解参考坐标系到第l+1开始的每一帧的变换矩阵R_initial, P_initial，保存在Pose中
if (i > l)
{
Matrix3d R_initial = c_Rotation[i - 1];
Vector3d P_initial = c_Translation[i - 1];
if(!solveFrameByPnP(R_initial, P_initial, i, sfm_f))
return false;
c_Rotation[i] = R_initial;
c_Translation[i] = P_initial;
c_Quat[i] = c_Rotation[i];
Pose[i].block<3, 3>(0, 0) = c_Rotation[i];
Pose[i].block<3, 1>(0, 3) = c_Translation[i];
}
// triangulate point based on the solve pnp result
triangulateTwoFrames(i, Pose[i], frame_num - 1, Pose[frame_num - 1], sfm_f);
}
//3: triangulate l-----l+1 l+2 ... frame_num -2
for (int i = l + 1; i < frame_num - 1; i++)
triangulateTwoFrames(l, Pose[l], i, Pose[i], sfm_f);
//4: solve pnp l-1; triangulate l-1 ----- l
// l-2 l-2 ----- l
//PNP求解参考坐标系到从第l-1到第0帧的每一帧之间的变换矩阵，并进行三角化
for (int i = l - 1; i >= 0; i--)
{
//solve pnp
Matrix3d R_initial = c_Rotation[i + 1];
Vector3d P_initial = c_Translation[i + 1];
if(!solveFrameByPnP(R_initial, P_initial, i, sfm_f))
return false;
c_Rotation[i] = R_initial;
c_Translation[i] = P_initial;
c_Quat[i] = c_Rotation[i];
Pose[i].block<3, 3>(0, 0) = c_Rotation[i];
Pose[i].block<3, 1>(0, 3) = c_Translation[i];
//triangulate
triangulateTwoFrames(i, Pose[i], l, Pose[l], sfm_f);
}
//5: triangulate all other points
//三角化其他未恢复的特征点。至此得到了滑动窗口中所有图像帧的位姿以及特征点的3d坐标
for (int j = 0; j < feature_num; j++)
{
if (sfm_f[j].state == true)
continue;
if ((int)sfm_f[j].observation.size() >= 2)
{
Vector2d point0, point1;
int frame_0 = sfm_f[j].observation[0].first;
point0 = sfm_f[j].observation[0].second;
int frame_1 = sfm_f[j].observation.back().first;
point1 = sfm_f[j].observation.back().second;
Vector3d point_3d;
triangulatePoint(Pose[frame_0], Pose[frame_1], point0, point1, point_3d);
sfm_f[j].state = true;
sfm_f[j].position[0] = point_3d(0);
sfm_f[j].position[1] = point_3d(1);
sfm_f[j].position[2] = point_3d(2);
//cout << "trangulated : " << frame_0 << " " << frame_1 << " 3d point : " << j << " " << point_3d.transpose() << endl;
}
}
/*
for (int i = 0; i < frame_num; i++)
{
q[i] = c_Rotation[i].transpose();
cout << "solvePnP q" << " i " << i <<" " <<q[i].w() << " " << q[i].vec().transpose() << endl;
}
for (int i = 0; i < frame_num; i++)
{
Vector3d t_tmp;
t_tmp = -1 * (q[i] * c_Translation[i]);
cout << "solvePnP t" << " i " << i <<" " << t_tmp.x() <<" "<< t_tmp.y() <<" "<< t_tmp.z() << endl;
}
*/
//full BA
//使用cares进行全局BA优化
ceres::Problem problem;
ceres::LocalParameterization* local_parameterization = new ceres::QuaternionParameterization();
//cout << " begin full BA " << endl;
for (int i = 0; i < frame_num; i++)
{
//double array for ceres
c_translation[i][0] = c_Translation[i].x();
c_translation[i][1] = c_Translation[i].y();
c_translation[i][2] = c_Translation[i].z();
c_rotation[i][0] = c_Quat[i].w();
c_rotation[i][1] = c_Quat[i].x();
c_rotation[i][2] = c_Quat[i].y();
c_rotation[i][3] = c_Quat[i].z();
problem.AddParameterBlock(c_rotation[i], 4, local_parameterization);
problem.AddParameterBlock(c_translation[i], 3);
if (i == l)
{
problem.SetParameterBlockConstant(c_rotation[i]);
}
if (i == l || i == frame_num - 1)
{
problem.SetParameterBlockConstant(c_translation[i]);
}
}
for (int i = 0; i < feature_num; i++)
{
if (sfm_f[i].state != true)
continue;
for (int j = 0; j < int(sfm_f[i].observation.size()); j++)
{
int l = sfm_f[i].observation[j].first;
ceres::CostFunction* cost_function = ReprojectionError3D::Create(
sfm_f[i].observation[j].second.x(),
sfm_f[i].observation[j].second.y());
problem.AddResidualBlock(cost_function, NULL, c_rotation[l], c_translation[l],
sfm_f[i].position);
}
}
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_SCHUR;
//options.minimizer_progress_to_stdout = true;
options.max_solver_time_in_seconds = 0.2;
ceres::Solver::Summary summary;
ceres::Solve(options, &problem, &summary);
//std::cout << summary.BriefReport() << "n";
if (summary.termination_type == ceres::CONVERGENCE || summary.final_cost < 5e-03)
{
//cout << "vision only BA converge" << endl;
}
else
{
//cout << "vision only BA not converge " << endl;
return false;
}
for (int i = 0; i < frame_num; i++)
{
q[i].w() = c_rotation[i][0];
q[i].x() = c_rotation[i][1];
q[i].y() = c_rotation[i][2];
q[i].z() = c_rotation[i][3];
q[i] = q[i].inverse();
//cout << "final q" << " i " << i <<" " <<q[i].w() << " " << q[i].vec().transpose() << endl;
}
//第l帧坐标系到各帧的变换矩阵，应将其转变为每一帧在第l帧坐标系上的位姿
for (int i = 0; i < frame_num; i++)
{
T[i] = -1 * (q[i] * Vector3d(c_translation[i][0], c_translation[i][1], c_translation[i][2]));
//cout << "final t" << " i " << i <<" " << T[i](0) <<" "<< T[i](1) <<" "<< T[i](2) << endl;
}
for (int i = 0; i < (int)sfm_f.size(); i++)
{
if(sfm_f[i].state)
sfm_tracked_points[sfm_f[i].id] = Vector3d(sfm_f[i].position[0], sfm_f[i].position[1], sfm_f[i].position[2]);
}
return true;
}
- 对于所有的图像帧，包括不在滑动窗口中的，提供初始的RT估计，然后solvePnP进行优化
// solve pnp for all frame
map<int, Vector3d>::iterator it;
map<double, ImageFrame>::iterator frame_it = all_image_frame.begin( );
for (int i = 0; frame_it != all_image_frame.end( ); frame_it++)
{
// provide initial guess
if((frame_it->first) == Headers[i].stamp.toSec())
{
frame_it->second.is_key_frame = true;
frame_it->second.R = Q[i].toRotationMatrix() * RIC[0].transpose();
frame_it->second.T = T[i];
i++;
continue;
}
if((frame_it->first) > Headers[i].stamp.toSec())
{
i++;
}
// 将滑窗内第i帧的变换矩阵当做初始值
Matrix3d R_inital = (Q[i].inverse()).toRotationMatrix();
Vector3d P_inital = - R_inital * T[i];
cv::Mat rvec, t, tmp_r;
cv::eigen2cv(R_inital, tmp_r);
cv::Rodrigues(tmp_r, rvec);
cv::eigen2cv(P_inital, t);
frame_it->second.is_key_frame = false;
vector<cv::Point3f> pts_3_vector;
vector<cv::Point2f> pts_2_vector;
for (auto &id_pts : frame_it->second.points)
{
int feature_id = id_pts.first;
for (auto &i_p : id_pts.second)
{
it = sfm_tracked_points.find(feature_id);
if(it != sfm_tracked_points.end())
{
Vector3d world_pts = it->second;
cv::Point3f pts_3(world_pts(0), world_pts(1), world_pts(2));
pts_3_vector.push_back(pts_3);
Vector2d img_pts = i_p.second.head<2>();
cv::Point2f pts_2(img_pts(0), img_pts(1));
pts_2_vector.push_back(pts_2);
}
}
}
if(pts_3_vector.size() < 6) {
cout << "pts_3_vector size " << pts_3_vector.size() << endl;
ROS_DEBUG("Not enough points for solve pnp !");
return false;
}
cv::Mat K = (cv::Mat_<double>(3, 3) << 1, 0, 0, 0, 1, 0, 0, 0, 1);
cv::Mat D;
if (! cv::solvePnP(pts_3_vector, pts_2_vector, K, D, rvec, t, true)) {
ROS_DEBUG("solve pnp fail!");
return false;
}
// PnP求解出的位姿要取逆
MatrixXd R_pnp;
MatrixXd T_pnp;
{
cv::Mat r;
cv::Rodrigues(rvec, r);
MatrixXd tmp_R_pnp;
cv::cv2eigen(r, tmp_R_pnp);
R_pnp = tmp_R_pnp.transpose();
cv::cv2eigen(t, T_pnp);
T_pnp = R_pnp * (-T_pnp);
}
// 转换到IMU坐标系下
frame_it->second.R = R_pnp * RIC[0].transpose();
frame_it->second.T = T_pnp;
}
- 6.进行视觉惯性联合初始化，imu与视觉对齐，获取绝对尺度s、陀螺仪偏置bg、加速度偏置ba、重力加速度G和每个IMU时刻的速度v
// 视觉与IMU对齐
if (visualInitialAlign())
return true;
else
{
ROS_INFO("misalign visual structure with IMU");
return false;
}
bool Estimator::visualInitialAlign()
该函数主要实现了陀螺仪的偏置校准(加速度偏置没有处理)，计算速度V[0:n]、重力g、尺度s。
同时更新了Bgs后，IMU测量量需要repropagate；得到尺度s和重力g的方向后，需更新所有图像帧在世界坐标系下的Ps、Rs、Vs。
bool Estimator::visualInitialAlign()
{
TicToc t_g;
VectorXd x;
//solve scale
// 要注意这个地方求解出的g是在C0坐标系下
//1.计算陀螺仪偏置，尺度，重力加速度和速度
bool result = VisualIMUAlignment(all_image_frame, Bgs, g, x);
if(!result) {
ROS_DEBUG("solve g failed!");
return false;
}
// change state
//2.获取所有图像帧的位姿Ps、Rs，并将其置为关键帧
for (int i = 0; i <= frame_count; i++)
{
Matrix3d Ri = all_image_frame[Headers[i].stamp.toSec()].R;
Vector3d Pi = all_image_frame[Headers[i].stamp.toSec()].T;
Ps[i] = Pi;
Rs[i] = Ri;
all_image_frame[Headers[i].stamp.toSec()].is_key_frame = true;
}
//将所有特征点的深度置为-1
VectorXd dep = f_manager.getDepthVector();
for (int i = 0; i < dep.size(); i++)
dep[i] = -1;
f_manager.clearDepth(dep);
//triangulat on cam pose , no tic
//3.重新计算特征点的深度
Vector3d TIC_TMP[NUM_OF_CAM];
for(int i = 0; i < NUM_OF_CAM; i++)
TIC_TMP[i].setZero();
ric[0] = RIC[0];
f_manager.setRic(ric);
f_manager.triangulate(Ps, &(TIC_TMP[0]), &(RIC[0]));
double s = (x.tail<1>())(0);
//4.陀螺仪的偏置bgs改变，重新计算预积分
for (int i = 0; i <= WINDOW_SIZE; i++)
{
pre_integrations[i]->repropagate(Vector3d::Zero(), Bgs[i]);
}
//5.将Ps、Vs、depth尺度s缩放后转变为相对于第0帧图像坐标系下
for (int i = frame_count; i >= 0; i--)
Ps[i] = s * Ps[i] - Rs[i] * TIC[0] - (s * Ps[0] - Rs[0] * TIC[0]);
int kv = -1;
map<double, ImageFrame>::iterator frame_i;
for (frame_i = all_image_frame.begin(); frame_i != all_image_frame.end(); frame_i++)
{
if(frame_i->second.is_key_frame)
{
kv++;
Vs[kv] = frame_i->second.R * x.segment<3>(kv * 3);
}
}
for (auto &it_per_id : f_manager.feature)
{
it_per_id.used_num = it_per_id.feature_per_frame.size();
if (!(it_per_id.used_num >= 2 && it_per_id.start_frame < WINDOW_SIZE - 2))
continue;
it_per_id.estimated_depth *= s;
}
//6.通过将重力旋转到z轴上，得到世界坐标系与摄像机坐标系c0之间的旋转矩阵rot_diff
Matrix3d R0 = Utility::g2R(g);
double yaw = Utility::R2ypr(R0 * Rs[0]).x();
R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;
g = R0 * g;
//Matrix3d rot_diff = R0 * Rs[0].transpose();
Matrix3d rot_diff = R0;
//7.所有变量从参考坐标系c0旋转到世界坐标系w
for (int i = 0; i <= frame_count; i++)
{
Ps[i] = rot_diff * Ps[i];
Rs[i] = rot_diff * Rs[i];
Vs[i] = rot_diff * Vs[i];
}
ROS_DEBUG_STREAM("g0 " << g.transpose());
ROS_DEBUG_STREAM("my R0 " << Utility::R2ypr(Rs[0]).transpose());
return true;
}
参考：
VINS-Mono代码解读——视觉惯性联合初始化 initialStructure sfm
VINS理论与代码详解4——初始化
最后
以上就是刻苦悟空为你收集整理的读懂VINS-Mono——初始化估计器初始化代码解析的全部内容，希望文章能够帮你解决读懂VINS-Mono——初始化估计器初始化代码解析所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复