数字信号中的各种频率

最近在重新学习数字信号处理，虽然之前选修过，然而当时只是为了应付考试囫囵吞枣的咽下了，基本没有理解其中的本质，遇到实际应用的时候就开始抓瞎，这种感觉相当难受，所以打算重新学习以下数字信号处理。
1、理解各种频率
各种频率称呼：频率、角频率、模拟频率、数字化频率、圆周频率、物理频率、归一化频率
我所能查到的各种频率基本上都列在这里，然后再来理解各自的含义。
频率：：是单位时间内完成周期性变化的次数，是描述周期运动频繁程度的量，常用符号f或ν表示，单位为秒分之一，符号为s-1

上面是频率的基本定义，需要注意的是这里说的单位时间，也就是1秒，换个角度来说，频率是和时间相关的量，脱离时间，频率也没有意义，且他的量纲是s-1;

再看一下信号邻域中的频率和生活中常见的机械领域的频率有何不同；任何复杂的信号都能由最简单的正余弦信号叠加而成，因此正余弦信号是基础，相当于用两个单位正交基构建全部的向量空间，所以通过研究正余弦信号就能知道复杂信号的特性。下面以最简单的正弦信号为例说明各种频率之间的关系。

中学中学过的正弦表达式是这样的：
y=sinx

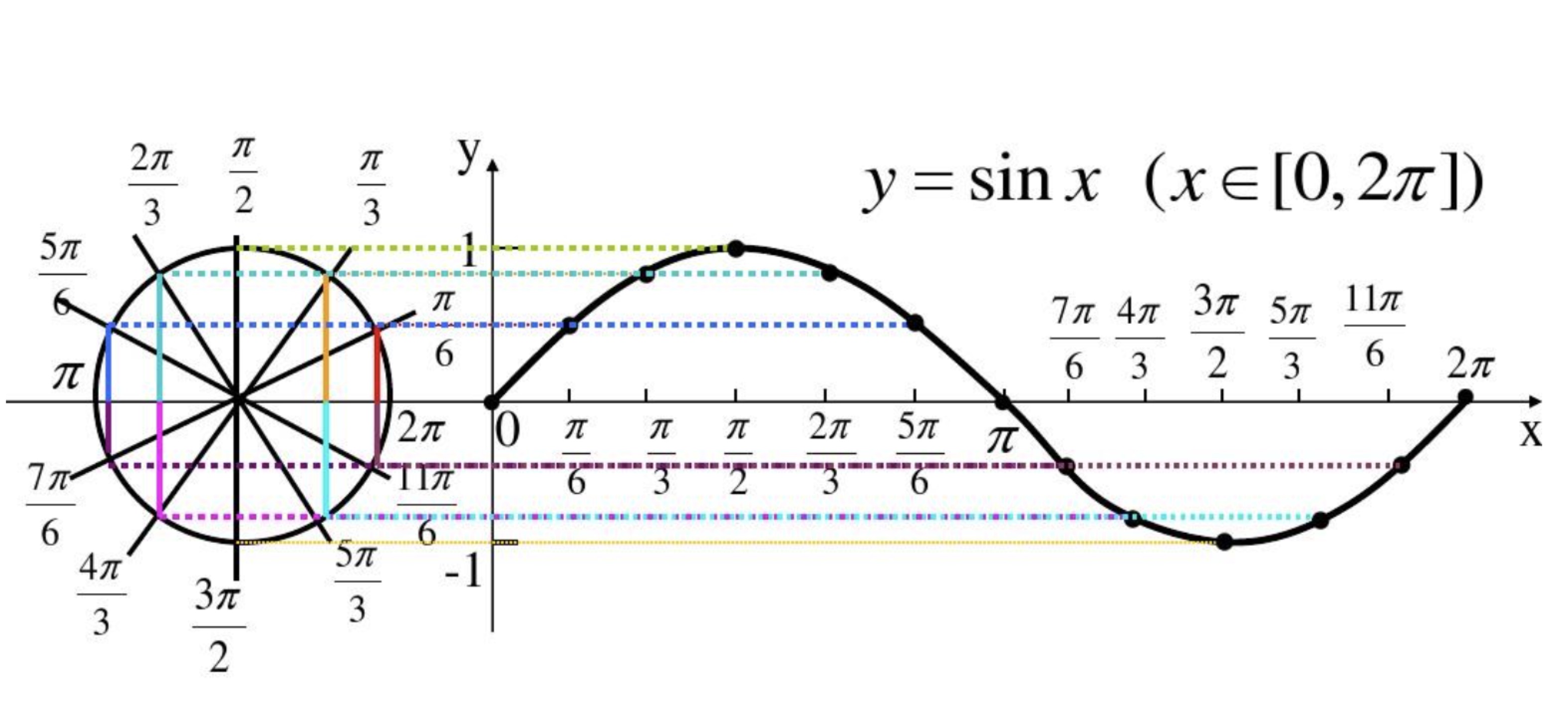
从图中可以看出，正弦信号的周期为2*pi，并且x代表的是相位，也就是圆周转过的对应的角度。

但再大学中正弦函数最常见的形式却是这样的
y=sin2✖pi✖f0✖t***
为什么要再前面加一个2pi和频率f0呢i呢？虽然道理上一样，但是表达式不同曾经让我纠结怀疑好久。

首先这两个表达式只是形式上不同，但实际意义是一样的，都是表示正弦信号，不同之处在于，上面的表达式变量是x,指的是相位，下面的表达式变量是t，这是时间的函数，时间经过换算就是相位。为什么要写成这种形式呢？我觉得这是因为现实生活中的信号都是关于时间的函数，比如A/D采集的信号，只能是关于时间的函数，为了方便表达，所以把正弦信号的周期2*pi加到变量中，这样一来，再处理的时候只需要知道时间，就能得到完整的信号，这也符合生活中的习惯。

那么问题又来了，为什么要加上频率f0呢？直接写成：
y=sin2✖pi✖t*****
的形式不好吗？
先看几个表达式：
y=sinx; 自变量是相位
y=sin2×pi×x; 自变量还是相位
y=sinf0×x; 自变量是时间，因为f0频率的单位是s-1，相乘后消掉，
y=sin2×pi×f0×x; 自变量是时间；
再来看x=1的时候表示的物理意义，假设f0=5Hz：
y=sin1; 相位1的sin值
y=sin2×pi×1; 相位2*pi的值
y=sin5×1; 相位5的值，但这时候不是一个整周其
y=sin2×pi×5×1; 相位10pi的值，表示该信号在1秒时刻的相位值

上面的几个表达式，哪个能够表达信号在1秒钟时刻的相位呢？
考虑到时间有单位s，因此必须要有频率才能将其消掉，所以最后两个表达式都可以， 但是y=sinf0×x; 这种形式在1秒钟时并不是整周期，而最后一种表达式恰恰时整周期
其实从量纲上也能看出来，如果x表示时间的话，由于相位是没有时间单位的，那么必须要有时间的倒数，将其消掉。所以才要把频率加上。

以上，总算明白了表达式写成y=sin2×pi×f0×x; 的原因。数学表达式的目的是为了应用服务，因此写成这种形式，可以让人一眼看出信号的最重要的两个性质：幅值和频率，非常方便。

信号的频率表示每秒钟内周期的个数，对于正弦信号来说，他的周期是2×pi，那么他一个周期的相位就是2×pi,但生活还有一些不是正弦信号的周期信号，可以随手画一个周期信号，并把它的周期定为1，那么此此时一个周期的相位就不再是2×pi，而是1，所以他的表达式中就不会有2pi。
所以，在看到有2pi的地方就知道这个信号的前提是正弦信号，正是因为正弦信号是自然界普遍存在的最简单的形式，所以在表达式中加上2pi才更有普适性。

频率描述的是每秒钟完成周期的次数，也叫做物理频率那么如果我要知道每秒钟走过多少相位了怎么办？乘上2pi，这也就是**模拟频率（角频率）**的由来。

那么数字频率和归一化频率又该如何理解呢？
首先，数字信号都是从连续信号中抽样的来的，以连续的信号
y=Asin(Ωt+θ)
为例，A是振幅，Ω 是频率，t 是时间变量，由于频率的单位是s-1，所以相乘后时间量纲会消掉，只有相位。Ω是数字信号中模拟频率的表示符。和上面分析额类似，我现在一看到Ω这个量就知道其中肯定有2pi；
我们以等间隔 T 对这个信号进行采样，也就是每隔 T 秒采一个点，每秒钟可以采 fs（1/T) 个点，信号的连续表达式是关于时间 t 的函数，经过采样后就变成了关于点数个数 n 的函数。n 经过等间隔采样的，时间间隔为T，那么采样点的位置n 乘以时间间隔T 就得到了相位，也就是每个间隔之间的相位，这就是数字频率的由来。

数字频率（圆周频率）：ω=ΩΤ

归一化频率 频率有大有小，比如1Hz,100Hz,10000Hz等等，如何统一这些表达呢？这就时归一化频率的作用。归一化频率是数字化采用的称呼，和采样频率fs有关，F=f/fs，物理频率除以采样频率即可求得归一化频率。由于奈奎斯特采样定理，最高的信号频率为fs/2对应归一化频率0.5， 这也就是为什么在matlab的fdtool工具中归一化频率为什么最大只到0.5的原因。

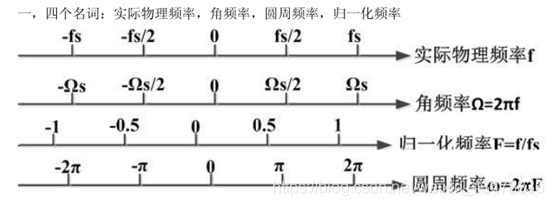
图源网络

这里基本上搞懂了各种频率的关系，接下来记录以下在matlab中绘制正弦信号时遇到的几个技巧。

以简单的正弦信号为例子：y=sint

t=1:0.01*pi:2*pi;
y=sin(t);

这表示把0-2pi分成100份，也就是在0-2pi之间采样100个点，这种方法不能直接看出我们熟悉的采样频率fs，频率f，采样点N之间的关系

fs=50;
N=50;
f=1;

n=0:N-1;
t=n/fs;

因为我希望在画图的时候知道到底有几个周期，希望能够在脑中形成大概的图形，那么如何才能做到呢？
对于信号来说，采样频率为fs，物理频率为f，

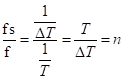
根据上面的公式可以知道，两种频率相除的物理意义是，每个周期内有多少个采样点，再用N/n就知道有几个周期了。
具体参考：理解采样频率和信号频率的关系

最后看一下离散型号的周期性，离散信号表达式为：
y=Asin(wn+θ)
如果w含有pi，那么就是周期，如果没有，那么就不是周期。这个理论可以根据周期性推到。

最后

以上就是忧伤月光为你收集整理的数字信号中的各种频率的全部内容，希望文章能够帮你解决数字信号中的各种频率所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。