使用 FFT 进行频谱分析

下面的示例说明了如何使用 FFT 函数进行频谱分析。FFT 的一个常用场景是确定一个时域噪声信号的频率分量。

首先创建一些数据。假设是以 1000 Hz 的频率对数据进行的采样。首先为数据构造一条时间轴，时间范围从 t = 0 至 t = 0.25，步长为 1 毫秒。然后，创建一个包含 50 Hz 和 120 Hz 频率的正弦波信号 x。

t = 0:.001:.25;
x = sin(2*pi*50*t) + sin(2*pi*120*t);

添加一些标准差为 2 的随机噪声以产生噪声信号 y。然后，通过对该噪声信号 y 绘图来了解该信号。

y = x + 2*randn(size(t));
plot(y(1:50))
title('Noisy time domain signal')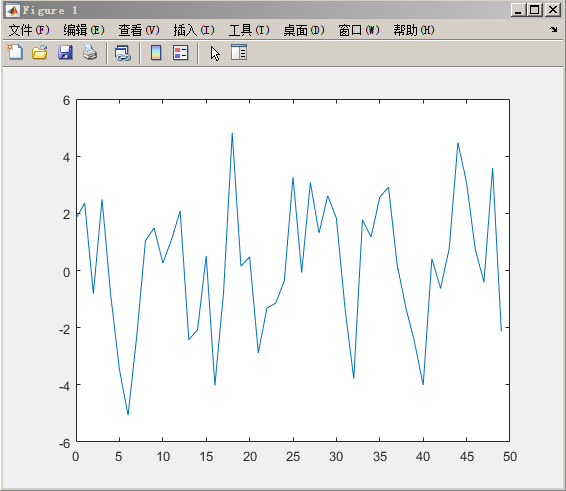

很明显，通过观察该信号很难确定频率分量；这就是频谱分析为什么被广泛应用的原因。

得到带噪声信号 y 的离散傅里叶变换很容易；执行快速傅里叶变换 (FFT) 即可实现。

Y = fft(y,251);

使用复共扼 (CONJ) 计算功率频谱密度，即测量不同频率下的能量。为前 127 个点构造一个频率轴，并使用该轴绘制结果图形。（其余的点是对称的。）

Pyy = Y.*conj(Y)/251;
f = 1000/251*(0:127);
plot(f,Pyy(1:128))
title('Power spectral density')
xlabel('Frequency (Hz)')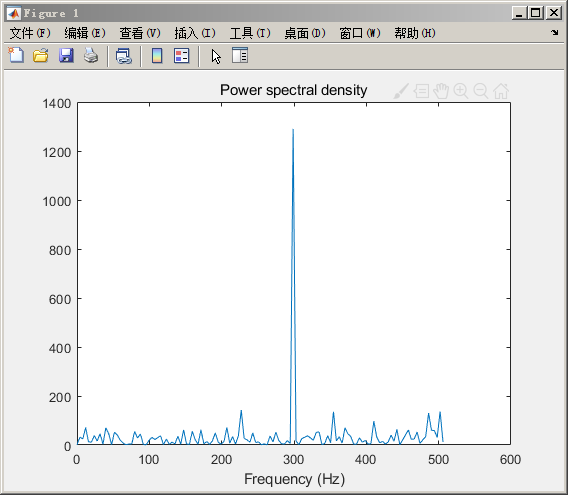

最后

以上就是忧虑帽子为你收集整理的使用 FFT 进行频谱分析的全部内容，希望文章能够帮你解决使用 FFT 进行频谱分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。