文章目录
- 1 概述
- 1.1 通信系统模型
- 1.2 信道
- 1.3 信道带宽 W
- 1.4 码元和码元传输速率
- 2 定理
- 2.1 奈奎斯特定理 - 无噪音
- 2.2 香农定理 - 有噪音
- 2.3 带宽、码元速率、数据速率 关系梳理
- 3 网工软考真题
1 概述
1.1 通信系统模型
- 通信的目的:传递信息
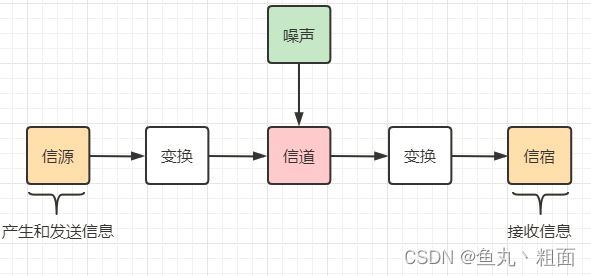
1.2 信道
- 信道:信息传输的通道
- 信源 和 信道 对应关系图(若不对应,则需要 变换)
| 信源产生的数据 | 信道的类型 | 信道的特点 | 举例 |
|---|---|---|---|
| 模拟数据 | 模拟信道 | 连续的,受噪音干扰时不易恢复 | 人说话的声音 |
| 数字数据 | 数字信道 | 离散的,受噪音干扰时容易恢复 | 电脑处理的数据 0,1 |
- 波形图
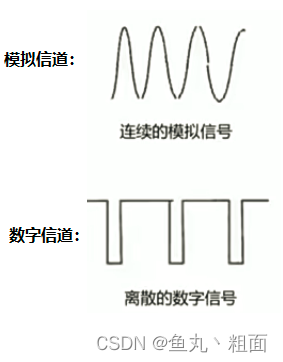
1.3 信道带宽 W
| 信道带宽 W | 计算公式 | 单位 | 解释说明 |
|---|---|---|---|
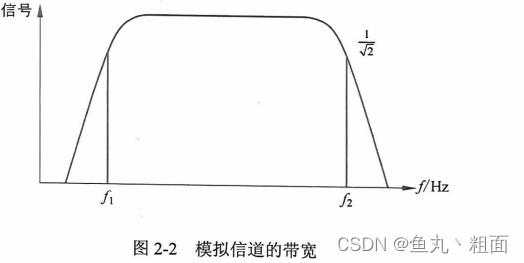
| 模拟信道 | W = f2 - f1 | 赫兹 Hz | f2 和 f1 分别表示:信道能通过的 最高、最低频率 |
| 数字信道 | W = max(数据传输速率) | 比特/秒(记作 bit/s、b/s、bps) | 带宽为信道能够达到的 最大数据传输速率 |
1.4 码元和码元传输速率
| 概念 | 定义 | 单位 | 说明 |
|---|---|---|---|
| 码元 | 一个 固定时长(码元长度) 的信号波形 | N 进制码元:码元种类 N 个 | |
| 码元传输速率 | 单位时间传输的 码元个数 | 波特(Baud) | 又称 波特率,简写 B |
| 信息传输速率 | 单位时间传输的 二进制码元个数 | bit/s |
- 一个码元携带信息量 n 位 与 码元种类数 N 的关系:
n
=
l
o
g
2
N
(
N
=
2
n
)
n=log_2N(N = 2^n)
n=log2N(N=2n)
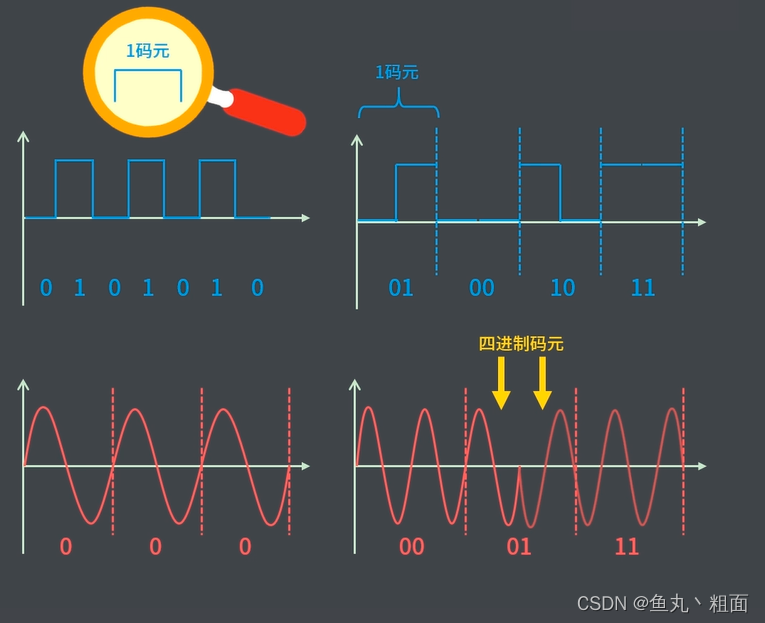
- 若码元取 2 个离散值,则一个码元携带 1 位信息 (2 个离散值:0,1 => 1位)
- 若码元取 4 个离散值,则一个码元携带 2 位信息(4 个离散值:00,01,10,11 => 2 位)
2 定理
2.1 奈奎斯特定理 - 无噪音
- 奈奎斯特定理(Nyquist’s Theorem):在一个 理想的(没有噪音环境) 的信道中,若信道带宽为 W,则
- 最大码元速率:B = 2W(Baud)
- 数据速率: R = B ∗ l o g 2 N = 2 W ∗ l o g 2 N ( b p s 或 b / s 、 b i t / s ) R = B * log_2N = 2W * log_2N(bps 或 b/s、bit/s) R=B∗log2N=2W∗log2N(bps或b/s、bit/s)
2.2 香农定理 - 有噪音
- 香农定理(Shannon’s Theorem):在一个 噪声信道 的信道中,若信道带宽为 W,则
- 极限数据速率: C = W l o g 2 ( 1 + S N ) ( b p s ) C = W log_2{(1 + frac{S}{N})}(bps) C=Wlog2(1+NS)(bps)
- 分贝与信噪比: d B = 10 l o g 10 S N dB = 10 log_{10}{ frac{S}{N}} dB=10log10NS
- 其中 S N frac{S}{N} NS:信噪比,S:信号的平均功率,N:噪声的平均功率
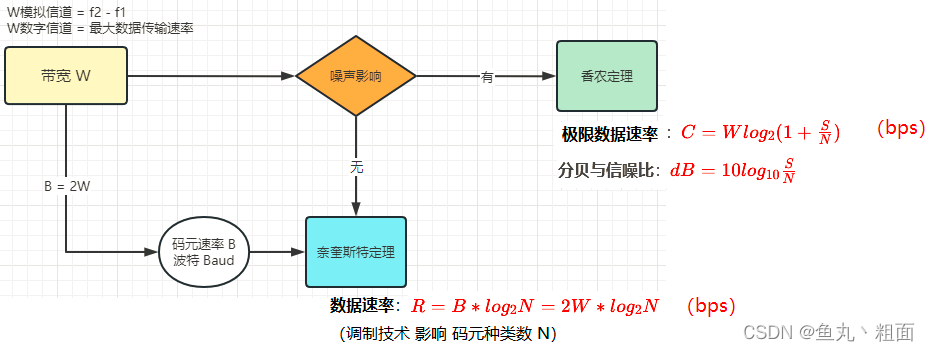
2.3 带宽、码元速率、数据速率 关系梳理
3 网工软考真题
【2018下半年 - 11】设信号的波特率为800Baud,采用幅度一相位复合调制技术,由4种幅度和8种相位组成16种码元,则信道的数据速率为( )。
A.1600 b/s
B.2400 b/s
C.3200 b/s
D.4800 b/s
参考答案:C
没说噪音,采用奈奎斯特定理: R = B ∗ l o g 2 N = 800 ∗ l o g 2 16 = 3200 b p s R = B * log_2N = 800 * log_216 = 3200 bps R=B∗log2N=800∗log216=3200bps
【2018下半年 - 16】设信道带宽为 1000Hz,信噪比为 30dB,则信道最大速率为()b/s
A.10000
B.20000
C.30000
D.40000
参考答案:A
信噪比 => 有噪音 => 香农定理: C = W l o g 2 ( 1 + S / N ) , d B = 10 l o g 10 ( S / N ) C = W log_2(1 + S/N),dB = 10log_{10}(S/N) C=Wlog2(1+S/N),dB=10log10(S/N)
信噪比 = 30 d B = 10 l o g 10 ( S / N ) 30dB = 10log_{10}(S/N) 30dB=10log10(S/N) => S / N = 1 0 3 = 1000 S/N = 10^3 = 1000 S/N=103=1000
最大速率 C = 1000 l o g 2 ( 1 + 1000 ) ≈ 10000 ,( 2 10 = 1024 ) C = 1000 log_2(1 + 1000) approx 10000,(2^{10} = 1024) C=1000log2(1+1000)≈10000,(210=1024)
【2017上半年 - 12,13】电话信道的频率为 0-4kHZ,若信噪比为 30dB,则信道容量为(12)kb/s,要达到此容量,至少需要(13)个信号状态。
(12) A.4
B.20
C.40
D.80
(13) A.4
B.8
C.16
D.32
参考答案:12=C,13=D
带宽 W = 4 - 0 = 4
信噪比 = 30db,根据 分贝与信噪比 公式: d B = 10 l o g 10 S N dB = 10 log_{10}{ frac{S}{N}} dB=10log10NS 可知, S / N = 1 0 3 S/N = 10^3 S/N=103
根据 香农定理 的极限数据速率: C = W l o g 2 ( 1 + S N ) C = W log_2{(1 + frac{S}{N})} C=Wlog2(1+NS) ,带入可知 C = 40
根据 奈奎斯特定理 的数据速率: R = B ∗ l o g 2 N = 2 W ∗ l o g 2 N R = B * log_2N = 2W * log_2N R=B∗log2N=2W∗log2N ,带入可知 N = 32
最后
以上就是超级诺言最近收集整理的关于数据通信基础 - 信道特性(奈奎斯特定理、香农定理 )1 概述2 信道特性3 网工软考真题的全部内容,更多相关数据通信基础内容请搜索靠谱客的其他文章。








发表评论 取消回复