数据分析（学习笔记）$$ \left[ \begin{array}{ccc} x{_1} & 1\ x{_2} & 1\ x{_3} & 1 \ x{_n} & 1 \ \end{array} \right ] \times \left[ \begin{array}{ccc} k\ b\ \end{array} \right ]案例：假设一帮孩子和家长出去旅游，去程坐的是bus，小孩票价为3元，家长票价为3.2元，共花了118.4；回程坐的是Train，小孩票价为3.5元，家长票价为3.6元，共

81 阅读 0 评论 54 点赞

我是靠谱客的博主闪闪过客，最近开发中收集的这篇文章主要介绍数据分析（学习笔记）$$ \left[ \begin{array}{ccc} x{_1} & 1\ x{_2} & 1\ x{_3} & 1 \ x{_n} & 1 \ \end{array} \right ] \times \left[ \begin{array}{ccc} k\ b\ \end{array} \right ]案例：假设一帮孩子和家长出去旅游，去程坐的是bus，小孩票价为3元，家长票价为3.2元，共花了118.4；回程坐的是Train，小孩票价为3.5元，家长票价为3.6元，共，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

数据分析

什么是数据分析？

数据分析是指用适当的统计分析方法对收集来的大量数据进行分析，提取有用信息和形成结论而对数据加以详细研究和概括总结的过程。

使用python做数据分析的常用库

numpy 基础数值算法
scipy 科学计算
matplotlib 数据可视化
pandas 序列高级函数

numpy概述

Numerical Python，数值的Python，补充了Python语言所欠缺的数值计算能力。
Numpy是其它数据分析及机器学习库的底层库。
Numpy完全标准C语言实现，运行效率充分优化。
Numpy开源免费。

numpy`历史`

1995年，Numeric，Python语言数值计算扩充。
2001年，Scipy->Numarray，多维数组运算。
2005年，Numeric+Numarray->Numpy。
2006年，Numpy脱离Scipy成为独立的项目。

numpy的核心：多维数组

代码简洁：减少Python代码中的循环。
底层实现：厚内核©+薄接口(Python)，保证性能。

numpy基础

ndarray数组

用np.ndarray类的对象表示n维数组

import numpy as np
ary = np.array([1, 2, 3, 4, 5, 6])
print(type(ary))

内存中的ndarray对象

元数据（metadata）

存储对目标数组的描述信息，如：dim count、dimensions、dtype、data等。

实际数据

完整的数组数据

将实际数据与元数据分开存放，一方面提高了内存空间的使用效率，另一方面减少对实际数据的访问频率，提高性能。

ndarray数组对象的特点

Numpy数组是同质数组，即所有元素的数据类型必须相同
Numpy数组的下标从0开始，最后一个元素的下标为数组长度减1

ndarray数组对象的创建

np.array(任何可被解释为Numpy数组的逻辑结构)

import numpy as np
a = np.array([1, 2, 3, 4, 5, 6])
print(a)

np.arange(起始值(0),终止值,步长(1))

import numpy as np
a = np.arange(0, 5, 1)
print(a)
b = np.arange(0, 10, 2)
print(b)

np.zeros(数组元素个数, dtype=‘类型’)

import numpy as np
a = np.zeros(10)
print(a)

np.ones(数组元素个数, dtype=‘类型’)

import numpy as np
a = np.ones(10)
print(a)

ndarray对象属性的基本操作

数组的维度： np.ndarray.shape

import numpy as np
ary = np.array([1, 2, 3, 4, 5, 6])
print(type(ary), ary, ary.shape)
#二维数组
ary = np.array([
    [1,2,3,4],
    [5,6,7,8]
])
print(type(ary), ary, ary.shape)

元素的类型： np.ndarray.dtype

import numpy as np
ary = np.array([1, 2, 3, 4, 5, 6])
print(type(ary), ary, ary.dtype)
#转换ary元素的类型
b = ary.astype(float)
print(type(b), b, b.dtype)
#转换ary元素的类型
c = ary.astype(str)
print(type(c), c, c.dtype)

数组元素的个数： np.ndarray.size

import numpy as np
ary = np.array([
    [1,2,3,4],
    [5,6,7,8]
])
#观察维度，size，len的区别
print(ary.shape, ary.size, len(ary))

数组元素索引(下标)

数组对象[…, 页号, 行号, 列号]

下标从0开始，到数组len-1结束。

import numpy as np
a = np.array([[[1, 2],
               [3, 4]],
              [[5, 6],
               [7, 8]]])
print(a, a.shape)
print(a[0])
print(a[0][0])
print(a[0][0][0])
print(a[0, 0, 0])
for i in range(a.shape[0]):
    for j in range(a.shape[1]):
        for k in range(a.shape[2]):
            print(a[i, j, k])

ndarray对象属性操作详解

Numpy的内部基本数据类型

类型名	类型表示符
布尔型	bool_
有符号整数型	int8(-128~127)/int16/int32/int64
无符号整数型	uint8(0~255)/uint16/uint32/uint64
浮点型	float16/float32/float64
复数型	complex64/complex128
字串型	str_，每个字符用32位Unicode编码表示

自定义复合类型

# 自定义复合类型
import numpy as np

data=[
	('zs', [90, 80, 85], 15),
	('ls', [92, 81, 83], 16),
	('ww', [95, 85, 95], 15)
]
#第一种设置dtype的方式
a = np.array(data, dtype='U3, 3int32, int32')
print(a)
print(a[0]['f0'], ":", a[1]['f1'])
print("=====================================")
#第二种设置dtype的方式
b = np.array(data, dtype=[('name', 'str_', 2),
                    ('scores', 'int32', 3),
                    ('ages', 'int32', 1)])
print(b[0]['name'], ":", b[0]['scores'])
print("=====================================")

#第三种设置dtype的方式
c = np.array(data, dtype={'names': ['name', 'scores', 'ages'],
                    'formats': ['U3', '3int32', 'int32']})
print(c[0]['name'], ":", c[0]['scores'], ":", c.itemsize)
print("=====================================")

#第四种设置dtype的方式  
d = np.array(data, dtype={'names': ('U3', 0),
                    'scores': ('3int32', 16),
                    'ages': ('int32', 28)})
print(d[0]['names'], d[0]['scores'], d.itemsize)

print("=====================================")

#第五种设置dtype的方式
e = np.array([0x1234, 0x5667],
             dtype=('u2', {'lowc': ('u1', 0),
                            'hignc': ('u1', 1)}))
print('%x' % e[0])
print('%x %x' % (e['lowc'][0], e['hignc'][0]))

print("=====================================")
#测试日期类型数组
f = np.array(['2011', '2012-01-01', '2013-01-01 01:01:01','2011-02-01'])
f = f.astype('M8[D]')
f = f.astype('int32')
print(f[3]-f[0])

print("=====================================")
a = np.array([[1 + 1j, 2 + 4j, 3 + 7j],
              [4 + 2j, 5 + 5j, 6 + 8j],
              [7 + 3j, 8 + 6j, 9 + 9j]])
print(a.T)

for x in a.flat:
	print(x.imag)

类型字符码

类型	字符码
np.bool_	?
np.int8/16/32/64	i1/i2/i4/i8
np.uint8/16/32/64	u1/u2/u4/u8
np.float/16/32/64	f2/f4/f8
np.complex64/128	c8/c16
np.str_	U<字符数>
np.datetime64	M8[Y] M8[M] M8[D] M8[h] M8[m] M8[s]

字节序前缀，用于多字节整数和字符串：
</>/[=]分别表示小端/大端/硬件字节序。

类型字符码格式

<字节序前缀><维度><类型><字节数或字符数>

3i4	释义
3i4	大端字节序，3个元素的一维数组，每个元素都是整型，每个整型元素占4个字节。
<(2,3)u8	小端字节序，6个元素2行3列的二维数组，每个元素都是无符号整型，每个无符号整型元素占8个字节。
U7	包含7个字符的Unicode字符串，每个字符占4个字节，采用默认字节序。

ndarray数组对象的维度操作

视图变维（数据共享）： reshape() 与 ravel()

import numpy as np
a = np.arange(1, 9)
print(a)		# [1 2 3 4 5 6 7 8]
b = a.reshape(2, 4)	#视图变维  : 变为2行4列的二维数组
print(b)
c = b.reshape(2, 2, 2) #视图变维    变为2页2行2列的三维数组
print(c)
d = c.ravel()	#视图变维	变为1维数组
print(d)

复制变维（数据独立）： flatten()

e = c.flatten()
print(e)
a += 10
print(a, e, sep='n')

就地变维：直接改变原数组对象的维度，不返回新数组

a.shape = (2, 4)
print(a)
a.resize(2, 2, 2)
print(a)

ndarray数组切片操作

#数组对象切片的参数设置与列表切面参数类似
#  步长+：默认切从首到尾
#  步长-：默认切从尾到首
数组对象[起始位置:终止位置:步长, ...]
#默认位置步长：1

import numpy as np
a = np.arange(1, 10)
print(a)  # 1 2 3 4 5 6 7 8 9
print(a[:3])  # 1 2 3
print(a[3:6])   # 4 5 6
print(a[6:])  # 7 8 9
print(a[::-1])  # 9 8 7 6 5 4 3 2 1
print(a[:-4:-1])  # 9 8 7
print(a[-4:-7:-1])  # 6 5 4
print(a[-7::-1])  # 3 2 1
print(a[::])  # 1 2 3 4 5 6 7 8 9
print(a[:])  # 1 2 3 4 5 6 7 8 9
print(a[::3])  # 1 4 7
print(a[1::3])  # 2 5 8
print(a[2::3])  # 3 6 9

多维数组的切片操作

import numpy as np
a = np.arange(1, 28)
a.resize(3,3,3)
print(a)
#切出1页 
print(a[1, :, :])		
#切出所有页的1行
print(a[:, 1, :])		
#切出0页的1行1列
print(a[0, :, 1])

ndarray数组的掩码操作

import numpy as np
a = np.arange(1, 10)
mask = [True, False,True, False,True, False,True, False,True, False]
print(a[mask])

多维数组的组合与拆分

垂直方向操作：

import numpy as np
a = np.arange(1, 7).reshape(2, 3)
b = np.arange(7, 13).reshape(2, 3)
# 垂直方向完成组合操作，生成新数组
c = np.vstack((a, b))
# 垂直方向完成拆分操作，生成两个数组
d, e = np.vsplit(c, 2)

水平方向操作：

import numpy as np
a = np.arange(1, 7).reshape(2, 3)
b = np.arange(7, 13).reshape(2, 3)
# 水平方向完成组合操作，生成新数组 
c = np.hstack((a, b))
# 水平方向完成拆分操作，生成两个数组
d, e = np.hsplit(c, 2)

长度不等的数组组合：

import numpy as np
a = np.array([1,2,3,4,5])
b = np.array([1,2,3,4])
# 填充b数组使其长度与a相同
b = np.pad(b, pad_width=(0, 1), mode='constant', constant_values=-1)
print(b)
# 垂直方向完成组合操作，生成新数组
c = np.vstack((a, b))
print(c)

深度方向操作：（3维）

import numpy as np
a = np.arange(1, 7).reshape(2, 3)
b = np.arange(7, 13).reshape(2, 3)
# 深度方向（3维）完成组合操作，生成新数组
i = np.dstack((a, b))
# 深度方向（3维）完成拆分操作，生成两个数组
k, l = np.dsplit(i, 2)

多维数组组合与拆分的相关函数：

# 通过axis作为关键字参数指定组合的方向，取值如下：
# 若待组合的数组都是二维数组：
#	0: 垂直方向组合
#	1: 水平方向组合
# 若待组合的数组都是三维数组：
#	0: 垂直方向组合
#	1: 水平方向组合
#	2: 深度方向组合
np.concatenate((a, b), axis=0)
# 通过给出的数组与要拆分的份数，按照某个方向进行拆分，axis的取值同上
np.split(c, 2, axis=0)

简单的一维数组组合方案

a = np.arange(1,9)		#[1, 2, 3, 4, 5, 6, 7, 8]
b = np.arange(9,17)		#[9,10,11,12,13,14,15,16]
#把两个数组摞在一起成两行
c = np.row_stack((a, b))
print(c)
#把两个数组组合在一起成两列
d = np.column_stack((a, b))
print(d)

ndarray类的其他属性

shape - 维度
dtype - 元素类型
size - 元素数量
ndim - 维数，len(shape)
itemsize - 元素字节数
nbytes - 总字节数 = size x itemsize
real - 复数数组的实部数组
imag - 复数数组的虚部数组
T - 数组对象的转置视图
flat - 扁平迭代器

import numpy as np
a = np.array([[1 + 1j, 2 + 4j, 3 + 7j],
              [4 + 2j, 5 + 5j, 6 + 8j],
              [7 + 3j, 8 + 6j, 9 + 9j]])
print(a.shape)
print(a.dtype)
print(a.ndim)
print(a.size)
print(a.itemsize)
print(a.nbytes)
print(a.real, a.imag, sep='n')
print(a.T)
print([elem for elem in a.flat])
b = a.tolist()
print(b)

matplotlib概述

matplotlib是python的一个绘图库。使用它可以很方便的绘制出版质量级别的图形。

matplotlib基本功能

基本绘图（在二维平面坐标系中绘制连续的线）
1. 设置线型、线宽和颜色
2. 设置坐标轴范围
3. 设置坐标刻度
4. 设置坐标轴
5. 图例
6. 特殊点
7. 备注
图形对象(图形窗口)
1. 子图
2. 刻度定位器
3. 刻度网格线
4. 半对数坐标
5. 散点图
6. 填充
7. 条形图
8. 饼图
9. 等高线图
10. 热成像图
11. 极坐标系
12. 三维曲面
13. 简单动画

matplotlib基本功能详解

基本绘图

绘图核心API

案例：绘制一条余弦曲线

import numpy as np
import matplotlib.pyplot as mp

# xarray: <序列> 水平坐标序列
# yarray: <序列> 垂直坐标序列
mp.plot(xarray, yarray)
#显示图表
mp.show()

绘制水平线与垂直线：

import numpy as np
import matplotlib.pyplot as mp

# vertical 绘制垂直线
mp.vlines(vval, ymin, ymax, ...)
# horizotal 绘制水平线
mp.hlines(xval, xmin, xmax, ...)
#显示图表
mp.show()

线型、线宽和颜色

案例：绘制一条正弦曲线

 
	#	数字
#color: <关键字参数> 颜色
	#	英文颜色单词 或 常见颜色英文单词首字母 或 #495434 或 (1,1,1) 或 (1,1,1,1)
#alpha: <关键字参数> 透明度
	#	浮点数值
mp.plot(xarray, yarray, linestyle='', linewidth=1, color='', alpha=0.5)

设置坐标轴范围

案例：把坐标轴范围设置为 -π ~ π

#x_limt_min:	<float> x轴范围最小值
#x_limit_max:	<float> x轴范围最大值
mp.xlim(x_limt_min, x_limit_max)
#y_limt_min:	<float> y轴范围最小值
#y_limit_max:	<float> y轴范围最大值
mp.ylim(y_limt_min, y_limit_max)

设置坐标刻度

案例：把横坐标的刻度显示为：0, π/2, π, 3π/2, 2π

#x_val_list: 	x轴刻度值序列
#x_text_list:	x轴刻度标签文本序列 [可选]
mp.xticks(x_val_list , x_text_list )
#y_val_list: 	y轴刻度值序列
#y_text_list:	y轴刻度标签文本序列 [可选]
mp.yticks(y_val_list , y_text_list )

刻度文本的特殊语法 – LaTex排版语法字符串

r'$x^n+y^n=z^n$',   r'$intfrac{1}{x} dx = ln |x| + C$',     r'$-frac{pi}{2}$'

$x^n+y^n=z^n, intfrac{1}{x} dx = ln |x| + C, -frac{pi}{2}$

设置坐标轴

坐标轴名：left / right / bottom / top

# 获取当前坐标轴字典，{'left':左轴,'right':右轴,'bottom':下轴,'top':上轴 }
ax = mp.gca()
# 获取其中某个坐标轴
axis = ax.spines['坐标轴名']
# 设置坐标轴的位置。 该方法需要传入2个元素的元组作为参数
# type: <str> 移动坐标轴的参照类型  一般为'data' (以数据的值作为移动参照值)
# val:  参照值
axis.set_position((type, val))
# 设置坐标轴的颜色
# color: <str> 颜色值字符串
axis.set_color(color)

案例：设置坐标轴至中心。

#设置坐标轴
ax = mp.gca()
axis_b = ax.spines['bottom']
axis_b.set_position(('data', 0))
axis_l = ax.spines['left']
axis_l.set_position(('data', 0))
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')

图例

显示两条曲线的图例，并测试loc属性。

# 再绘制曲线时定义曲线的label
# label: <关键字参数 str> 支持LaTex排版语法字符串
mp.plot(xarray, yarray ... label='', ...)
# 设置图例的位置
# loc: <关键字参数> 制定图例的显示位置 (若不设置loc，则显示默认位置)
#	 ===============   =============
#    Location String   Location Code
#    ===============   =============
#    'best'            0
#    'upper right'     1
#    'upper left'      2
#    'lower left'      3
#    'lower right'     4
#    'right'           5
#    'center left'     6
#    'center right'    7
#    'lower center'    8
#    'upper center'    9
#    'center'          10
#    ===============   =============
mp.legend(loc='')

特殊点

案例：绘制当x=3π/4时两条曲线上的特殊点。

# xarray: <序列> 所有需要标注点的水平坐标组成的序列
# yarray: <序列> 所有需要标注点的垂直坐标组成的序列
mp.scatter(xarray, yarray, 
           marker='', 		#点型 ~ matplotlib.markers
           s='', 			#大小
           edgecolor='', 	#边缘色
           facecolor='',	#填充色
           zorder=3			#绘制图层编号 （编号越大，图层越靠上）
)

marker点型可参照：help(matplotlib.markers)

也可参照附录： matplotlib point样式

备注

案例：为在某条曲线上的点添加备注，指明函数方程与值。

# 在图表中为某个点添加备注。包含备注文本，备注箭头等图像的设置。
mp.annotate(
    r'$frac{pi}{2}$',			#备注中显示的文本内容
    xycoords='data',			#备注目标点所使用的坐标系（data表示数据坐标系）
    xy=(x, y),	 				#备注目标点的坐标
    textcoords='offset points',	#备注文本所使用的坐标系（offset points表示参照点的偏移坐标系）
    xytext=(x, y),				#备注文本的坐标
    fontsize=14,				#备注文本的字体大小
    arrowprops=dict()			#使用字典定义文本指向目标点的箭头样式
)

arrowprops参数使用字典定义指向目标点的箭头样式

#arrowprops字典参数的常用key
arrowprops=dict(
	arrowstyle='',		#定义箭头样式
    connectionstyle=''	#定义连接线的样式
)

箭头样式（arrowstyle）字符串如下

============   =============================================
Name           Attrs
============   =============================================
  '-'          None
  '->'         head_length=0.4,head_width=0.2
  '-['         widthB=1.0,lengthB=0.2,angleB=None
  '|-|'        widthA=1.0,widthB=1.0
  '-|>'        head_length=0.4,head_width=0.2
  '<-'         head_length=0.4,head_width=0.2
  '<->'        head_length=0.4,head_width=0.2
  '<|-'        head_length=0.4,head_width=0.2
  '<|-|>'      head_length=0.4,head_width=0.2
  'fancy'      head_length=0.4,head_width=0.4,tail_width=0.4
  'simple'     head_length=0.5,head_width=0.5,tail_width=0.2
  'wedge'      tail_width=0.3,shrink_factor=0.5
============   =============================================

连接线样式（connectionstyle）字符串如下

============   =============================================
Name           Attrs
============   =============================================
  'angle' 		angleA=90,angleB=0,rad=0.0
  'angle3' 		angleA=90,angleB=0`   
  'arc'			angleA=0,angleB=0,armA=None,armB=None,rad=0.0
  'arc3' 		rad=0.0
  'bar' 		armA=0.0,armB=0.0,fraction=0.3,angle=None
============   =============================================

图形对象（图形窗口）

案例：绘制两个窗口，一起显示。

# 手动构建 matplotlib 窗口
mp.figure(
    '',					#窗口标题栏文本 
    figsize=(4, 3),		#窗口大小 <元组>
    dpi=120,			#像素密度
	facecolor=''		#图表背景色
)
mp.show()

mp.figure方法不仅可以构建一个新窗口，如果已经构建过title='xxx’的窗口，又使用figure方法构建了title=‘xxx’ 的窗口的话，mp将不会创建新的窗口，而是把title='xxx’的窗口置为当前操作窗口。

设置当前窗口的参数

案例：测试窗口相关参数

# 设置图表标题 显示在图表上方
mp.title(title, fontsize=12)
# 设置水平轴的文本
mp.xlabel(x_label_str, fontsize=12)
# 设置垂直轴的文本
mp.ylabel(y_label_str, fontsize=12)
# 设置刻度参数   labelsize设置刻度字体大小
mp.tick_params(..., labelsize=8, ...)
# 设置图表网格线  linestyle设置网格线的样式
	#	-  or solid 粗线
	#   -- or dashed 虚线
	#   -. or dashdot 点虚线
	#   :  or dotted 点线
mp.grid(linestyle='')
# 设置紧凑布局，把图表相关参数都显示在窗口中
mp.tight_layout()

子图

矩阵式布局

绘制矩阵式子图布局相关API：

mp.figure('Subplot Layout', facecolor='lightgray')
# 拆分矩阵
	# rows:	行数
    # cols:	列数
    # num:	编号
mp.subplot(rows, cols, num)
	#	1 2 3
	#	4 5 6
	#	7 8 9 
mp.subplot(3, 3, 5)		#操作3*3的矩阵中编号为5的子图
mp.subplot(335)			#简写

案例：绘制9宫格矩阵式子图，每个子图中写一个数字。

mp.figure('Subplot Layout', facecolor='lightgray')

for i in range(9):
	mp.subplot(3, 3, i+1)
	mp.text(
		0.5, 0.5, i+1, 
		ha='center',
		va='center',
		size=36,
		alpha=0.5,
		withdash=False
	)
	mp.xticks([])
	mp.yticks([])

mp.tight_layout()
mp.show()

网格式布局

网格式布局支持单元格的合并。

绘制网格式子图布局相关API：

import matplotlib.gridspec as mg
mp.figure('Grid Layout', facecolor='lightgray')
# 调用GridSpec方法拆分网格式布局
# rows:	行数
# cols:	列数
# gs = mg.GridSpec(rows, cols)	拆分成3行3列
gs = mg.GridSpec(3, 3)	
# 合并0行与0、1列为一个子图表
mp.subplot(gs[0, :2])
mp.text(0.5, 0.5, '1', ha='center', va='center', size=36)
mp.show()

案例：绘制一个自定义网格布局。

import matplotlib.gridspec as mg
mp.figure('GridLayout', facecolor='lightgray')
gridsubs = mp.GridSpec(3, 3)
# 合并0行、0/1列为一个子图
mp.subplot(gridsubs[0, :2])
mp.text(0.5, 0.5, 1, ha='center', va='center', size=36)
mp.tight_layout()
mp.xticks([])
mp.yticks([])

自由式布局

自由式布局相关API：

mp.figure('Flow Layout', facecolor='lightgray')
# 设置图标的位置，给出左下角点坐标与宽高即可
# left_bottom_x: 坐下角点x坐标
# left_bottom_x: 坐下角点y坐标
# width:		 宽度
# height:		 高度
# mp.axes([left_bottom_x, left_bottom_y, width, height])
mp.axes([0.03, 0.03, 0.94, 0.94])
mp.text(0.5, 0.5, '1', ha='center', va='center', size=36)
mp.show()

案例：测试自由式布局，定位子图。

mp.figure('FlowLayout', facecolor='lightgray')

mp.axes([0.1, 0.2, 0.5, 0.3])
mp.text(0.5, 0.5, 1, ha='center', va='center', size=36)
mp.show()

刻度定位器

刻度定位器相关API：

# 获取当前坐标轴
ax = mp.gca()
# 设置水平坐标轴的主刻度定位器
ax.xaxis.set_major_locator(mp.NullLocator())
# 设置水平坐标轴的次刻度定位器为多点定位器，间隔0.1
ax.xaxis.set_minor_locator(mp.MultipleLocator(0.1))

案例：绘制一个数轴。

mp.figure('Locators', facecolor='lightgray')
# 获取当前坐标轴
ax = mp.gca()
# 隐藏除底轴以外的所有坐标轴
ax.spines['left'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
# 将底坐标轴调整到子图中心位置
ax.spines['bottom'].set_position(('data', 0))
# 设置水平坐标轴的主刻度定位器
ax.xaxis.set_major_locator(mp.NullLocator())
# 设置水平坐标轴的次刻度定位器为多点定位器，间隔0.1
ax.xaxis.set_minor_locator(mp.MultipleLocator(0.1))
# 标记所用刻度定位器类名 
mp.text(5, 0.3, 'NullLocator()', ha='center', size=12)

案例：使用for循环测试刻度器样式：

locators = ['mp.NullLocator()', 'mp.MaxNLocator(nbins=4)']
	
for i, locator in enumerate(locators):
    mp.subplot(len(locators), 1, i+1)
	mp.xlim(0, 10)
	mp.ylim(-1, 1)
	mp.yticks([])
	# 获取当前坐标轴
	ax = mp.gca()
	# 隐藏除底轴以外的所有坐标轴
	ax.spines['left'].set_color('none')
	ax.spines['top'].set_color('none')
	ax.spines['right'].set_color('none')
	# 将底坐标轴调整到子图中心位置
	ax.spines['bottom'].set_position(('data', 0))
	# 设置水平坐标轴的主刻度定位器
	ax.xaxis.set_major_locator(eval( ))
	# 设置水平坐标轴的次刻度定位器为多点定位器，间隔0.1
	ax.xaxis.set_minor_locator(mp.MultipleLocator(0.1))
	mp.plot(np.arange(11), np.zeros(11), c='none')
	# 标记所用刻度定位器类名
	mp.text(5, 0.3, locator, ha='center', size=12)

常用刻度器如下

# 空定位器：不绘制刻度
mp.NullLocator()
# 最大值定位器：
# 最多绘制nbins+1个刻度
mp.MaxNLocator(nbins=3)
# 定点定位器：根据locs参数中的位置绘制刻度
mp.FixedLocator(locs=[0, 2.5, 5, 7.5, 10])
# 自动定位器：由系统自动选择刻度的绘制位置
mp.AutoLocator()
# 索引定位器：由offset确定起始刻度，由base确定相邻刻度的间隔
mp.IndexLocator(offset=0.5, base=1.5)
# 多点定位器：从0开始，按照参数指定的间隔(缺省1)绘制刻度
mp.MultipleLocator()
# 线性定位器：等分numticks-1份，绘制numticks个刻度
mp.LinearLocator(numticks=21)
# 对数定位器：以base为底，绘制刻度
mp.LogLocator(base=2)

刻度网格线

绘制刻度网格线的相关API：

ax = mp.gca()
#绘制刻度网格线
ax.grid(
    which='',		# 'major'/'minor' <-> '主刻度'/'次刻度' 
    axis='',		# 'x'/'y'/'both' <-> 绘制x或y轴
    linewidth=1, 	# 线宽
    linestyle='', 	# 线型
    color='',		# 颜色
	alpha=0.5		# 透明度
)

案例：绘制曲线 [1, 10, 100, 1000, 100, 10, 1]，然后设置刻度网格线，测试刻度网格线的参数。

y = np.array([1, 10, 100, 1000, 100, 10, 1])
mp.figure('Normal & Log', facecolor='lightgray')
mp.subplot(211)
mp.title('Normal', fontsize=20)
mp.ylabel('y', fontsize=14)
ax = mp.gca()
ax.xaxis.set_major_locator(mp.MultipleLocator(1.0))
ax.xaxis.set_minor_locator(mp.MultipleLocator(0.1))
ax.yaxis.set_major_locator(mp.MultipleLocator(250))
ax.yaxis.set_minor_locator(mp.MultipleLocator(50))
mp.tick_params(labelsize=10)
ax.grid(which='major', axis='both', linewidth=0.75,
        linestyle='-', color='orange')
ax.grid(which='minor', axis='both', linewidth=0.25,
        linestyle='-', color='orange')
mp.plot(y, 'o-', c='dodgerblue', label='plot')
mp.legend()

半对数坐标

y轴将以指数方式递增。基于半对数坐标绘制第二个子图，表示曲线：[1, 10, 100, 1000, 100, 10, 1]。

mp.figure('Grid', facecolor='lightgray')
y = [1, 10, 100, 1000, 100, 10, 1]
mp.semilogy(y)
mp.show()

散点图

可以通过每个点的坐标、颜色、大小和形状表示不同的特征值。

身高	体重	性别	年龄段	种族
180	80	男	中年	亚洲
160	50	女	青少	美洲

绘制散点图的相关API：

mp.scatter(
    x, 					# x轴坐标数组
    y,					# y轴坐标数组
    marker='', 			# 点型
    s=10,				# 大小
    color='',			# 颜色
    edgecolor='', 		# 边缘颜色
    facecolor='',		# 填充色
    zorder=''			# 图层序号
)

numpy.random提供了normal函数用于产生符合正态分布的随机数

n = 100
# 172:	期望值
# 10:	标准差
# n:	数字生成数量
x = np.random.normal(172, 20, n)
y = np.random.normal(60, 10, n)

案例：绘制平面散点图。

mp.figure('scatter', facecolor='lightgray')
mp.title('scatter')
mp.scatter(x, y)
mp.show()

设置点的颜色

mp.scatter(x, y, c='red')			#直接设置颜色
d = (x-172)**2 + (y-60)**2
mp.scatter(x, y, c=d, cmap='jet')	#以c作为参数，取cmap颜色映射表中的颜色值

cmap颜色映射表参照附件：cmap颜色映射表

填充

以某种颜色自动填充两条曲线的闭合区域。

mp.fill_between(
	x,				# x轴的水平坐标
    sin_x,			# 下边界曲线上点的垂直坐标
    cos_x,			# 上边界曲线上点的垂直坐标
    sin_x<cos_x, 	# 填充条件，为True时填充
    color='', 		# 填充颜色
    alpha=0.2		# 透明度
)

案例：绘制两条曲线： sin_x = sin(x) cos_x = cos(x / 2) / 2 [0-8π]

n = 1000
x = np.linspace(0, 8 * np.pi, n)
sin_y = np.sin(x)
cos_y = np.cos(x / 2) / 2
mp.figure('Fill', facecolor='lightgray')
mp.title('Fill', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(x, sin_y, c='dodgerblue',
        label=r'$y=sin(x)$')
mp.plot(x, cos_y, c='orangered',
        label=r'$y=frac{1}{2}cos(frac{x}{2})$')
mp.fill_between(x, cos_y, sin_y, cos_y < sin_y,
                color='dodgerblue', alpha=0.5)
mp.fill_between(x, cos_y, sin_y, cos_y > sin_y,
                color='orangered', alpha=0.5)
mp.legend()
mp.show()

条形图（柱状图）

绘制柱状图的相关API：

mp.figure('Bar', facecolor='lightgray')
mp.bar(
	x,				# 水平坐标数组
    y,				# 柱状图高度数组
    width,			# 柱子的宽度
    color='', 		# 填充颜色
    label='',		#
    alpha=0.2		#
)

案例：先以柱状图绘制苹果12个月的销量，然后再绘制橘子的销量。

apples = np.array([30, 25, 22, 36, 21, 29, 20, 24, 33, 19, 27, 15])
oranges = np.array([24, 33, 19, 27, 35, 20, 15, 27, 20, 32, 20, 22])
mp.figure('Bar'  , facecolor='lightgray')
mp.title('Bar', font size=20)
mp.xlabel('Month', fontsize=14)
mp.ylabel('Price', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(axis='y', linestyle=':')
mp.ylim((0, 40))
x = np.arange(len(apples))
mp.bar(x-0.2, apples, 0.4, color='dodgerblue',label='Apple')
mp.bar(x + 0.2, oranges, 0.4, color='orangered',label='Orange', alpha=0.75)
mp.xticks(x, [
    'Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun',
    'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'])
mp.legend()
mp.show()

饼图

绘制饼状图的基本API：

mp.pie(
    values, 		# 值列表		
    spaces, 		# 扇形之间的间距列表
    labels, 		# 标签列表
    colors, 		# 颜色列表
    '%d%%',			# 标签所占比例格式
	shadow=True, 	# 是否显示阴影
    startangle=90	# 逆时针绘制饼状图时的起始角度
    radius=1		# 半径
)

案例：绘制饼状图显示5门语言的流行程度：

mp.figure('pie', facecolor='lightgray')
#整理数据
values = [26, 17, 21, 29, 11]
spaces = [0.05, 0.01, 0.01, 0.01, 0.01]
labels = ['Python', 'JavaScript',
          'C++', 'Java', 'PHP']
colors = ['dodgerblue', 'orangered',
          'limegreen', 'violet', 'gold']
mp.figure('Pie', facecolor='lightgray')
mp.title('Pie', fontsize=20)
# 等轴比例
mp.axis('equal')
mp.pie(
    values, 		# 值列表		
    spaces, 		# 扇形之间的间距列表
    labels, 		# 标签列表
    colors, 		# 颜色列表
    '%d%%',			# 标签所占比例格式
	shadow=True, 	# 是否显示阴影
    startanle=90	# 逆时针绘制饼状图时的起始角度
    radius=1		# 半径
)

附录

matplotlib colors颜色字符串

在这里插入图片描述

matplotlib point样式

在这里插入图片描述

laTeX语法表示数学符号示例

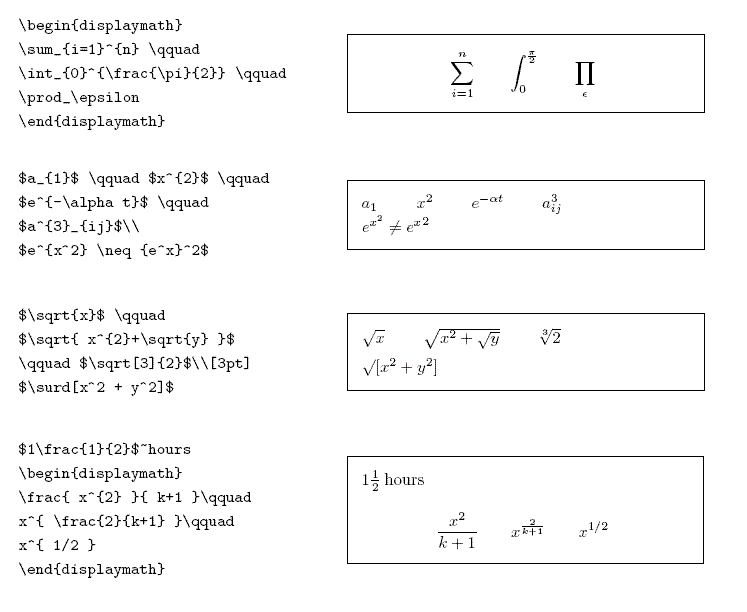
在这里插入图片描述

LaTeX语法集合

在这里插入图片描述

cmap颜色映射表

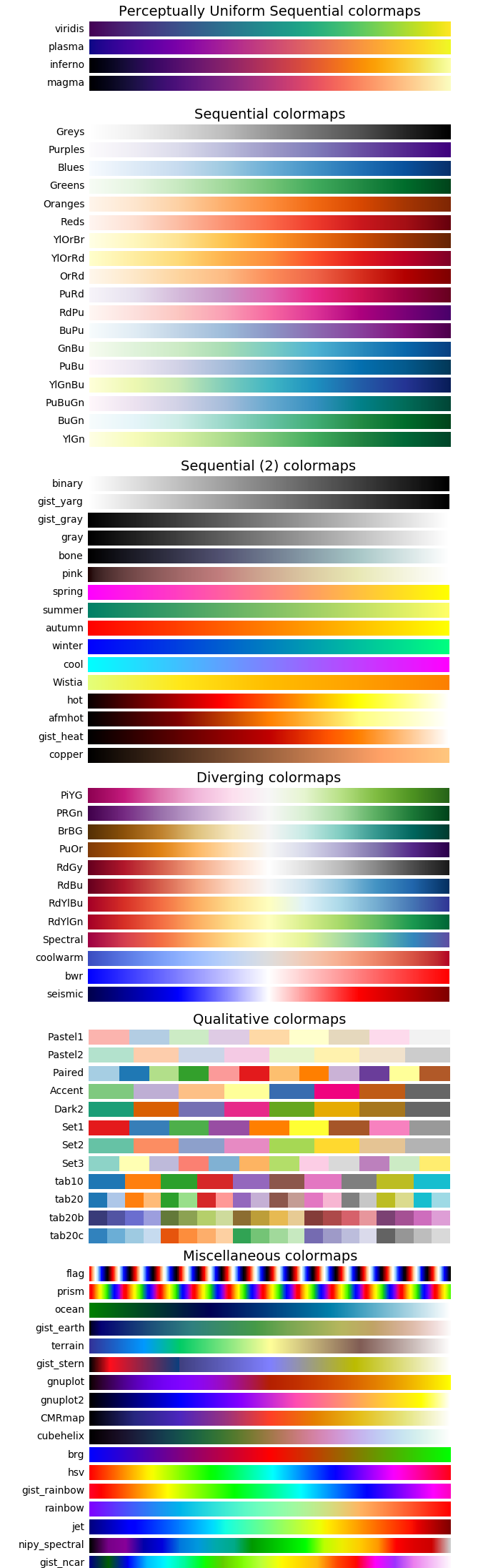
在这里插入图片描述

等高线图

组成等高线需要网格点坐标矩阵，也需要每个点的高度。所以等高线属于3D数学模型范畴。

绘制等高线的相关API：

mp.contourf(x, y, z, 8, cmap='jet')
cntr = mp.contour(
    x, 					# 网格坐标矩阵的x坐标 （2维数组）
    y, 					# 网格坐标矩阵的y坐标 （2维数组）
    z, 					# 网格坐标矩阵的z坐标 （2维数组）
    8, 					# 把等高线绘制成8部分
    colors='black',		# 等高线的颜色
	linewidths=0.5		# 线宽
)

案例：生成网格坐标矩阵，并且绘制等高线：

n = 1000
# 生成网格化坐标矩阵
x, y = np.meshgrid(np.linspace(-3, 3, n),
                   np.linspace(-3, 3, n))
# 根据每个网格点坐标，通过某个公式计算z高度坐标
z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2)
mp.figure('Contour', facecolor='lightgray')
mp.title('Contour', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
# 绘制等高线图
mp.contourf(x, y, z, 8, cmap='jet')
cntr = mp.contour(x, y, z, 8, colors='black',
                  linewidths=0.5)
# 为等高线图添加高度标签
mp.clabel(cntr, inline_spacing=1, fmt='%.1f',
          fontsize=10)
mp.show()

热成像图

用图形的方式显示矩阵及矩阵中值的大小
1 2 3
4 5 6
7 8 9

绘制热成像图的相关API：

# 把矩阵z图形化，使用cmap表示矩阵中每个元素值的大小
# origin: 坐标轴方向
#    upper: 缺省值，原点在左上角
#    lower: 原点在左下角
mp.imshow(z, cmap='jet', origin='low')

使用颜色条显示热度值：

mp.colorbar()

极坐标系

与笛卡尔坐标系不同，某些情况下极坐标系适合显示与角度有关的图像。例如雷达等。极坐标系可以描述极径ρ与极角θ的线性关系。

mp.figure("Polar", facecolor='lightgray')
mp.gca(projection='polar')
mp.title('Porlar', fontsize=20)
mp.xlabel(r'$theta$', fontsize=14)
mp.ylabel(r'$rho$', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.show()

在极坐标系中绘制曲线：

#准备数据
t = np.linspace(0, 4*np.pi, 1000)
r = 0.8 * t
mp.plot(t, r)
mp.show()

案例，在极坐标系中绘制正弦函数。 y=3 sin(6x)

x = np.linspace(0, 6*np.pi, 1000)
y = 3*np.sin(6*x)
mp.plot(x, y)

3D图像绘制

matplotlib支持绘制三维曲面。若希望绘制三维曲面，需要使用axes3d提供的3d坐标系。

from mpl_toolkits.mplot3d import axes3d
ax3d = mp.gca(projection='3d')   # class axes3d

matplotlib支持绘制三维点阵、三维曲面、三维线框图：

ax3d.scatter(..)		# 绘制三维点阵
ax3d.plot_surface(..)	# 绘制三维曲面
ax3d.plot_wireframe(..)	# 绘制三维线框图

3d散点图的绘制相关API：

ax3d.scatter(
    x, 				# x轴坐标数组
    y,				# y轴坐标数组
    marker='', 		# 点型
    s=10,			# 大小
    zorder='',		# 图层序号
    color='',		# 颜色
    edgecolor='', 	# 边缘颜色
    facecolor='',	# 填充色
    c=v,			# 颜色值 根据cmap映射应用相应颜色
    cmap=''			# 
)

案例：随机生成3组坐标，程标准正态分布规则，并且绘制它们。

n = 1000
x = np.random.normal(0, 1, n)
y = np.random.normal(0, 1, n)
z = np.random.normal(0, 1, n)
d = np.sqrt(x ** 2 + y ** 2 + z ** 2)
mp.figure('3D Scatter')
ax = mp.gca(projection='3d')  # 创建三维坐标系
mp.title('3D Scatter', fontsize=20)
ax.set_xlabel('x', fontsize=14)
ax.set_ylabel('y', fontsize=14)
ax.set_zlabel('z', fontsize=14)
mp.tick_params(labelsize=10)
ax.scatter(x, y, z, s=60, c=d, cmap='jet_r', alpha=0.5)
mp.show()

3d平面图的绘制相关API：

ax3d.plot_surface(
    x, 					# 网格坐标矩阵的x坐标 （2维数组）
    y, 					# 网格坐标矩阵的y坐标 （2维数组）
    z, 					# 网格坐标矩阵的z坐标 （2维数组）
    rstride=30,			# 行跨距
    cstride=30, 		# 列跨距
    cmap='jet'			# 颜色映射
)

案例：绘制3d平面图

n = 1000
# 生成网格化坐标矩阵
x, y = np.meshgrid(np.linspace(-3, 3, n),
                   np.linspace(-3, 3, n))
# 根据每个网格点坐标，通过某个公式计算z高度坐标
z = (1 - x/2 + x**5 + y**3) * np.exp(-x**2 - y**2)
mp.figure('3D', facecolor='lightgray')

ax3d = mp.gca(projection='3d')
mp.title('3D', fontsize=20)
ax3d.set_xlabel('x', fontsize=14)
ax3d.set_ylabel('y', fontsize=14)
ax3d.set_zlabel('z', fontsize=14)
mp.tick_params(labelsize=10)
# 绘制3D平面图
# rstride: 行跨距
# cstride: 列跨距 
ax3d.plot_surface(x,y,z,rstride=30,cstride=30, cmap='jet')

案例：3d线框图的绘制

# 绘制3D平面图 
# rstride: 行跨距
# cstride: 列跨距 
ax3d.plot_wireframe(x,y,z,rstride=30,cstride=30, 
	linewidth=1, color='dodgerblue')

简单动画

动画即是在一段时间内快速连续的重新绘制图像的过程。

matplotlib提供了方法用于处理简单动画的绘制。定义update函数用于即时更新图像。

import matplotlib.animation as ma
#定义更新函数行为
def update(number):
    pass
# 每隔10毫秒执行一次update更新函数，作用于mp.gcf()当前窗口对象
# mp.gcf()：	获取当前窗口
# update：	更新函数
# interval：	间隔时间（单位：毫秒）
anim = ma.FuncAnimation(mp.gcf(), update, interval=10)
mp.show()

案例：随机生成各种颜色的100个气泡。让他们不断的增大。

#自定义一种可以存放在ndarray里的类型，用于保存一个球
ball_type = np.dtype([
	('position', float, 2),  # 位置(水平和垂直坐标)
    ('size', float, 1),      # 大小
    ('growth', float, 1),    # 生长速度
    ('color', float, 4)])    # 颜色(红、绿、蓝和透明度)

#随机生成100个点对象
n = 100
balls = np.zeros(100, dtype=ball_type)
balls['position']=np.random.uniform(0, 1, (n, 2))
balls['size']=np.random.uniform(40, 70, n)
balls['growth']=np.random.uniform(10, 20, n)
balls['color']=np.random.uniform(0, 1, (n, 4))

mp.figure("Animation", facecolor='lightgray')
mp.title("Animation", fontsize=14)
mp.xticks 
mp.yticks(())

sc = mp.scatter(
	balls['position'][:, 0], 
	balls['position'][:, 1], 
	balls['size'], 
	color=balls['color'], alpha=0.5)
	
#定义更新函数行为
def update(number):
	balls['size'] += balls['growth']
	#每次让一个气泡破裂，随机生成一个新的
	boom_ind = number % n
	balls[boom_ind]['size']=np.random.uniform(40, 70, 1)
	balls[boom_ind]['position']=np.random.uniform(0, 1, (1, 2))
	# 重新设置属性
	sc.set_sizes(balls['size'])
	sc.set_offsets(balls['position'])
	
# 每隔30毫秒执行一次update更新函数，作用于mp.gcf()当前窗口对象
# mp.gcf()：	获取当前窗口
# update：		更新函数
# interval：	间隔时间（单位：毫秒）
anim = ma.FuncAnimation(mp.gcf(), update, interval=30)
mp.show()

使用生成器函数提供数据，实现动画绘制

在很多情况下，绘制动画的参数是动态获取的，matplotlib支持定义generator生成器函数，用于生成数据，把生成的数据交给update函数更新图像：

import matplotlib.animation as ma
#定义更新函数行为
def update(data):
    t, v = data
    ...
    pass

def generator():
	yield t, v
        
# 每隔10毫秒将会先调用生成器，获取生成器返回的数据，
# 把生成器返回的数据交给并且调用update函数，执行更新图像函数
anim = ma.FuncAnimation(mp.gcf(), update, generator,interval=10)

案例：绘制信号曲线：y=sin(2 * π * t) * exp(sin(0.2 * π * t))，数据通过生成器函数生成，在update函数中绘制曲线。

mp.figure("Signal", facecolor='lightgray')
mp.title("Signal", fontsize=14)
mp.xlim(0, 10)
mp.ylim(-3, 3)
mp.grid(linestyle='--', color='lightgray', alpha=0.5)
pl = mp.plot([], [], color='dodgerblue', label='Signal')[0]
pl.set_data([],[])

x = 0

def update(data):
	t, v = data
	x, y = pl.get_data()
	x.append(t)
	y.append(v)
	#重新设置数据源
	pl.set_data(x, y)
	#移动坐标轴
	if(x[-1]>10):
		mp.xlim(x[-1]-10, x[-1])

def y_generator():
	global x
	y = np.sin(2 * np.pi * x) * np.exp(np.sin(0.2 * np.pi * x))
	yield (x, y)
	x += 0.05

anim = ma.FuncAnimation(mp.gcf(), update, y_generator, interval=20)
mp.tight_layout()
mp.show()

numpy常用函数

加载文件

numpy提供了函数用于加载逻辑上可被解释为二维数组的文本文件，格式如下：

数据项1 <分隔符> 数据项2 <分隔符> ... <分隔符> 数据项n
例如：
AA,AA,AA,AA,AA
BB,BB,BB,BB,BB
...
或：
AA:AA:AA:AA:AA
BB:BB:BB:BB:BB
...

调用numpy.loadtxt()函数可以直接读取该文件并且获取ndarray数组对象：

import numpy as np
# 直接读取该文件并且获取ndarray数组对象 
# 返回值：
#     unpack=False：返回一个二维数组
#     unpack=True： 多个一维数组
np.loadtxt(
    '../aapl.csv',			# 文件路径
    delimiter=',',			# 分隔符
    usecols=(1, 3),			# 读取1、3两列 （下标从0开始）
    unpack=False,			# 是否按列拆包
    dtype='U10, f8',		# 制定返回每一列数组中元素的类型
    converters={1:func}		# 转换器函数字典
)

案例：读取aapl.csv文件，得到文件中的信息：

import numpy as np
import datetime as dt
# 日期转换函数
def dmy2ymd(dmy):
	dmy = str(dmy, encoding='utf-8')
	time = dt.datetime.strptime(dmy, '%d-%m-%Y').date()
	t = time.strftime('%Y-%m-%d')
	return t
dates, opening_prices,highest_prices, 
	lowest_prices, closeing_pric es  = np.loadtxt(
    '../data/aapl.csv',		# 文件路径
    delimiter=',',			# 分隔符
    usecols=(1, 3, 4, 5, 6),			# 读取1、3两列 （下标从0开始）
    unpack=True,
    dtype='M8[D], f8, f8, f8, f8',		# 制定返回每一列数组中元素的类型
    converters={1:dmy2ymd})

案例：使用matplotlib绘制K线图

绘制dates与收盘价的折线图：

import numpy as np
import datetime as dt
import matplotlib.pyplot as mp
import matplotlib.dates as md

# 绘制k线图，x为日期
mp.figure('APPL K', facecolor='lightgray')
mp.title('APPL K')
mp.xlabel('Day', fontsize=12)
mp.ylabel('Price', fontsize=12)

#拿到坐标轴
ax = mp.gca()
#设置主刻度定位器为周定位器（每周一显示主刻度文本）
ax.xaxis.set_major_locator( md.WeekdayLocator(byweekday=md.MO) )
ax.xaxis.set_major_formatter(md.DateFormatter('%d %b %Y'))
#设置次刻度定位器为日定位器 
ax.xaxis.set_minor_locator(md.DayLocator())
mp.tick_params(labelsize=8)
dates = dates.astype(md.datetime.datetime)

mp.plot(dates, opening_prices, color='dodgerblue',
		linestyle='-')
mp.gcf().autofmt_xdate()
mp.show()

绘制每一天的蜡烛图：

#绘制每一天的蜡烛图
#填充色：涨为白色，跌为绿色
rise = closeing_prices >= opening_prices
color = np.array([('white' if x else 'limegreen') for x in rise])
#边框色：涨为红色，跌为绿色
edgecolor = np.array([('red' if x else 'limegreen') for x in rise])

#绘制线条
mp.bar(dates, highest_prices - lowest_prices, 0.1,
	lowest_prices, color=edgecolor)
#绘制方块
mp.bar(dates, closeing_prices - opening_prices, 0.8,
	opening_prices, color=color, edgecolor=edgecolor)

算数平均值

S = [s1, s2, ..., sn]

样本中的每个值都是真值与误差的和。

算数平均值：
m = (s1 + s2 + ... + sn) / n

算数平均值表示对真值的无偏估计。

np.mean(array)

案例：计算收盘价的算术平均值。

import numpy as np
closing_prices = np.loadtxt(
    '../../data/aapl.csv', delimiter=',',
    usecols=(6), unpack=True)
mean = 0
for closing_price in closing_prices:
    mean += closing_price
mean /= closing_prices.size
print(mean)
mean = np.mean(closing_prices)
print(mean)

加权平均值

样本：S = [s₁, s₂, …, s_n]

权重：W = [w₁, w₂, …, w_n]

加权平均值：a = (s₁w₁+s₂w₂+…+s_nw_n)/(w₁+w₂+…+w_n)

np.average(closing_prices, weights=volumes)

VWAP - 成交量加权平均价格（成交量体现了市场对当前交易价格的认可度，成交量加权平均价格将会更接近这支股票的真实价值）

import numpy as np
closing_prices, volumes = np.loadtxt(
    '../../data/aapl.csv', delimiter=',',
    usecols=(6, 7), unpack=True)
vwap, wsum = 0, 0
for closing_price, volume in zip(
        closing_prices, volumes):
    vwap += closing_price * volume
    wsum += volume
vwap /= wsum
print(vwap)
vwap = np.average(closing_prices, weights=volumes)
print(vwap)

TWAP - 时间加权平均价格（时间越晚权重越高，参考意义越大）

import datetime as dt
import numpy as np

def dmy2days(dmy):
    dmy = str(dmy, encoding='utf-8')
    date = dt.datetime.strptime(dmy, '%d-%m-%Y').date()
    days = (date - dt.date.min).days
    return days

days, closing_prices = np.loadtxt(
    '../../data/aapl.csv', delimiter=',',
    usecols=(1, 6), unpack=True,
    converters={1: dmy2days})
twap = np.average(closing_prices, weights=days)
print(twap)

数据分析 DAY04

numpy常用函数

最值

np.max() np.min() np.ptp()： 返回一个数组中最大值/最小值/极差

import numpy as np
# 产生9个介于[10, 100)区间的随机数
a = np.random.randint(10, 100, 9)
print(a)
print(np.max(a), np.min(a), np.ptp(a))

np.argmax() mp.argmin()： 返回一个数组中最大/最小元素的下标

print(np.argmax(a), np.argmin(a))

np.maximum() np.minimum()： 将两个同维数组中对应元素中最大/最小元素构成一个新的数组

print(np.maximum(a, b), np.minimum(a, b), sep='n')

案例：评估AAPL股票的波动性。

import numpy as np
highest_prices, lowest_prices = np.loadtxt(
    '../../data/aapl.csv', delimiter=',',
    usecols=(4, 5), dtype='f8, f8', unpack=True)
max_price = np.max(highest_prices)
min_price = np.min(lowest_prices)
print(min_price, '~', max_price)

查看AAPL股票最大最小值的日期，分析为什么这一天出现最大最小值。

import numpy as np
dates, highest_prices, lowest_prices = np.loadtxt(
    '../../data/aapl.csv', delimiter=',',
    usecols=(1, 4, 5), dtype='U10, f8, f8',
    unpack=True)
max_index = np.argmax(highest_prices)
min_index = np.argmin(lowest_prices)
print(dates[min_index], dates[max_index])

观察最高价与最低价的波动范围，分析这支股票底部是否坚挺。

import numpy as np
dates, highest_prices, lowest_prices = np.loadtxt(
    '../../data/aapl.csv', delimiter=',',
    usecols=(1, 4, 5), dtype='U10, f8, f8',
    unpack=True)
highest_ptp = np.ptp(highest_prices)
lowest_ptp = np.ptp(lowest_prices)
print(lowest_ptp, highest_ptp)

中位数

将多个样本按照大小排序，取中间位置的元素。

若样本数量为奇数，中位数为最中间的元素

1 2000 3000 4000 10000000

若样本数量为偶数，中位数为最中间的两个元素的平均值

1 2000 3000 4000 5000 10000000

案例：分析中位数的算法，测试numpy提供的中位数API：

import numpy as np
closing_prices = np.loadtxt( '../../data/aapl.csv', 
	delimiter=',', usecols=(6), unpack=True)
size = closing_prices.size
sorted_prices = np.msort(closing_prices)
median = (sorted_prices[int((size - 1) / 2)] + sorted_prices[int(size / 2)]) / 2
print(median)
median = np.median(closing_prices)
print(median)

标准差

样本：S = [s1, s2, …, sn]
平均值：m = (s1+s2+…+sn)/n
离差：D = [d1, d2, …, dn], di = si-m
离差方：Q = [q1, q2, …, qn], qi = di²
总体方差：v = (q1+q2+…+qn)/n
总体标准差：s = sqrt(v)，方均根
样本方差：v’ = (q1+q2+…+qn)/(n-1)
样本标准差：s’ = sqrt(v’)，方均根

import numpy as np
closing_prices = np.loadtxt(
    '../../data/aapl.csv', delimiter=',', usecols=(6), unpack=True)
mean = np.mean(closing_prices)         # 算数平均值
devs = closing_prices - mean           # 离差
dsqs = devs ** 2                       # 离差方
pvar = np.sum(dsqs) / dsqs.size        # 总体方差
pstd = np.sqrt(pvar)                   # 总体标准差
svar = np.sum(dsqs) / (dsqs.size - 1)  # 样本方差
sstd = np.sqrt(svar)                   # 样本标准差
print(pstd, sstd)
pstd = np.std(closing_prices)          # 总体标准差
sstd = np.std(closing_prices, ddof=1)  # 样本标准差
print(pstd, sstd)

案例应用

时间数据处理

案例：统计每个周一、周二、…、周五的收盘价的平均值，并放入一个数组。

import datetime as dt
import numpy as np

# 转换器函数：将日-月-年格式的日期字符串转换为星期
def dmy2wday(dmy):
    dmy = str(dmy, encoding='utf-8')
    date = dt.datetime.strptime(dmy, '%d-%m-%Y').date()
    wday = date.weekday()  # 用 周日
    return wday

wdays, closing_prices = np.loadtxt('../data/aapl.csv', delimiter=',',
    	usecols=(1, 6), unpack=True, converters={1: dmy2wday})

ave_closing_prices = np.zeros(5)
for wday in range(ave_closing_prices.size):
    ave_closing_prices[wday] = closing_prices[wdays == wday].mean()

for wday, ave_closing_price in zip(
    	['MON', 'TUE', 'WED', 'THU', 'FRI'],
        ave_closing_prices):
    print(wday, np.round(ave_closing_price, 2))

数组的轴向汇总

案例：汇总每周的最高价，最低价，开盘价，收盘价。

def func(data):
    pass
#func 	处理函数
#axis 	轴向 [0,1]
#array 	数组
np.apply_along_axis(func, axis, array)

沿着数组中所指定的轴向，调用处理函数，并将每次调用的返回值重新组织成数组返回。

移动均线

收盘价5日均线：从第五天开始，每天计算最近五天的收盘价的平均值所构成的一条线。

移动均线算法：

(a+b+c+d+e)/5
(b+c+d+e+f)/5
(c+d+e+f+g)/5
...
(f+g+h+i+j)/5

在K线图中绘制5日均线图

import datetime as dt
import numpy as np
import matplotlib.pyplot as mp
import matplotlib.dates as md

def dmy2ymd(dmy):
    dmy = str(dmy, encoding='utf-8')
    date = dt.datetime.strptime(dmy, '%d-%m-%Y').date()
    ymd = date.strftime('%Y-%m-%d')
    return ymd

dates, closing_prices = np.loadtxt('../data/aapl.csv', delimiter=',',
    usecols=(1, 6), unpack=True, dtype='M8[D], f8', converters={1: dmy2ymd})
sma51 = np.zeros(closing_prices.size - 4)
for i in range(sma51.size):
    sma51[i] = closing_prices[i:i + 5].mean()
# 开始绘制5日均线
mp.figure('Simple Moving Average', facecolor='lightgray')
mp.title('Simple Moving Average', fontsize=20)
mp.xlabel('Date', fontsize=14)
mp.ylabel('Price', fontsize=14)
ax = mp.gca()
# 设置水平坐标每个星期一为主刻度
ax.xaxis.set_major_locator(md.WeekdayLocator( byweekday=md.MO))
# 设置水平坐标每一天为次刻度
ax.xaxis.set_minor_locator(md.DayLocator())
# 设置水平坐标主刻度标签格式
ax.xaxis.set_major_formatter(md.DateFormatter('%d %b %Y'))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
dates = dates.astype(md.datetime.datetime)
mp.plot(dates, closing_prices, c='lightgray', label='Closing Price')
mp.plot(dates[4:], sma51, c='orangered', label='SMA-5(1)')
mp.legend()
mp.gcf().autofmt_xdate()
mp.show()

卷积

激励函数：g(t)

单位激励下的响应函数：f(t)

绘制时间（t）与痛感（h）的函数关系图。

a = [1 2 3 4 5] （理解为某单位时间的击打力度序列）

b = [6 7 8] （理解为痛感系数序列）

c = numpy.convolve(a, b, 卷积类型)

                40  61  82         - 有效卷积(valid)
            19  40  61  82  67     - 同维卷积(same)
        6   19  40  61  82  67  40 - 完全卷积(full)
0   0   1   2   3   4   5   0   0
8   7   6
    8   7   6
        8   7   6
            8   7   6
                8   7   6
                    8   7   6
                        8    7   6

5日移动均线序列可以直接使用卷积实现

a = [a, b, c, d, e, f, g, h, i, j] 
b = [1/5, 1/5, 1/5, 1/5, 1/5]

使用卷积函数numpy.convolve(a, b, 卷积类型)实现5日均线

sma52 = np.convolve( closing_prices, np.ones(5) / 5, 'valid')
mp.plot(dates[4:], sma52, c='limegreen', alpha=0.5,
        linewidth=6, label='SMA-5(2)')

使用卷积函数numpy.convolve(a, b, 卷积类型)实现10日均线

sma10 = np.convolve(closing_prices, np.ones(10) / 10, 'valid')
mp.plot(dates[9:], sma10, c='dodgerblue', label='SMA-10')

使用卷积函数numpy.convolve(a, b, 卷积类型)实现加权5日均线

weights = np.exp(np.linspace(-1, 0, 5))
weights /= weights.sum()
ema5 = np.convolve(closing_prices, weights[::-1], 'valid')
mp.plot(dates[4:], sma52, c='limegreen', alpha=0.5,
        linewidth=6, label='SMA-5')

布林带

布林带由三条线组成：

中轨：移动平均线

上轨：中轨+2x5日收盘价标准差（顶部的压力）

下轨：中轨-2x5日收盘价标准差（底部的支撑力）

布林带收窄代表稳定的趋势，布林带张开代表有较大的波动空间的趋势。

绘制5日均线的布林带

weights = np.exp(np.linspace(-1, 0, 5))
weights /= weights.sum()
em5 = np.convolve(closing_prices, weights[::-1], 'valid')
stds = np.zeros(em5.size)
for i in range(stds.size):
    stds[i] = closing_prices[i:i + 5].std()
stds *= 2
lowers = medios - stds
uppers = medios + stds

mp.plot(dates, closing_prices, c='lightgray', label='Closing Price')
mp.plot(dates[4:], medios, c='dodgerblue', label='Medio')
mp.plot(dates[4:], lowers, c='limegreen', label='Lower')
mp.plot(dates[4:], uppers, c='orangered', label='Upper')

线性模型

什么是线性关系？

1 2 3 4 5

60 65 70 75 ？

线性预测

假设一组数据符合一种线型规律，那么就可以预测未来将会出现的数据。

a	b	c	d	e	f	?

ax + by + cz = d
bx + cy + dz = e
cx + dy + ez = f

$c\ b & c & d\ c & d & e\ end{array} right ] times left[ begin{array}{ccc} x\ y\ z\ end{array} right ]= left[ begin{array}{ccc} d\ e\ f\ end{array} right ]$

根据线性模型的特点可以通过一组历史数据求出线性关系系数x, y, z，从而预测d、e、f下的一个数据是多少。

线性预测需要使用历史数据进行检验，让预测结果可信度更高

案例：使用线性预测，预测下一天的收盘价。

# 整理五元一次方程组    最终获取一组股票走势预测值
N = 5
pred_prices = np.zeros(closing_prices.size - 2 * N + 1)
for i in range(pred_prices.size):
    a = np.zeros((N, N))
    for j in range(N):
        a[j, ] = closing_prices[i + j:i + j + N]
    b = closing_prices[i + N:i + N * 2]
    x = np.linalg.lstsq(a, b)[0]
    pred_prices[i] = b.dot(x)
# 由于预测的是下一天的收盘价，所以想日期数组中追加一个元素，为下一个工作日的日期
dates = dates.astype(md.datetime.datetime)
mp.plot(dates, closing_prices, 'o-', c='lightgray', label='Closing Price')
dates = np.append(dates, dates[-1] + pd.tseries.offsets.BDay())
mp.plot(dates[2 * N:], pred_prices, 'o-',c='orangered', 
        linewidth=3,label='Predicted Price')
mp.legend()
mp.gcf().autofmt_xdate() 
mp.show()

线性拟合

线性拟合可以寻求与一组散点走向趋势规律相适应的线型表达式方程。

有一组散点描述时间序列下的股价：

[x1, y1], [x2, y2], [x3, y3], 
...
[xn, yn]

根据线型 y=kx + b 方程可得：

kx1 + b = y1
kx2 + b = y2
kx3 + b = y3
...
kxn + b = yn

$$
left[ begin{array}{ccc}
x{_1} & 1
x{_2} & 1
x{_3} & 1
x{_n} & 1
end{array}
right ]
times
left[ begin{array}{ccc}
k
b
end{array}
right ]

left[ begin{array}{ccc}
y{_1}
y{_2}
y{_3}
y{_n}
end{array}
right ]
$$
样本过多，每两组方程即可求得一组k与b的值。np.linalg.lstsq(a, b) 可以通过最小二乘法求出所有结果中拟合误差最小的k与b的值。

案例：利用线型拟合画出股价的趋势线

绘制趋势线（趋势可以表示为最高价、最低价、收盘价的均值）：

dates, opening_prices, highest_prices, 
    lowest_prices, closing_prices = np.loadtxt('../data/aapl.csv', delimiter=',',
        usecols=(1, 3, 4, 5, 6), unpack=True,dtype='M8[D], f8, f8, f8, f8',
        converters={1: dmy2ymd})
trend_points = (highest_prices + lowest_prices + closing_prices) / 3
days = dates.astype(int)
a = np.column_stack((days, np.ones_like(days)))
x = np.linalg.lstsq(a, trend_points)[0]
trend_line = days * x[0] + x[1]
mp.figure('Trend', facecolor='lightgray')
mp.title('Trend', fontsize=20)
mp.xlabel('Date', fontsize=14)
mp.ylabel('Price', fontsize=14)
ax = mp.gca()
ax.xaxis.set_major_locator(md.WeekdayLocator(byweekday=md.MO))
ax.xaxis.set_minor_locator(md.DayLocator())
ax.xaxis.set_major_formatter(md.DateFormatter('%d %b %Y'))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
dates = dates.astype(md.datetime.datetime)
rise = closing_prices - opening_prices >= 0.01
fall = opening_prices - closing_prices >= 0.01
fc = np.zeros(dates.size, dtype='3f4')
ec = np.zeros(dates.size, dtype='3f4')
fc[rise], fc[fall] = (1, 1, 1), (0.85, 0.85, 0.85)
ec[rise], ec[fall] = (0.85, 0.85, 0.85), (0.85, 0.85, 0.85)
mp.bar(dates, highest_prices - lowest_prices, 0,lowest_prices, color=fc, edgecolor=ec)
mp.bar(dates, closing_prices - opening_prices, 0.8,opening_prices, color=fc, 
       edgecolor=ec)
mp.scatter(dates, trend_points, c='dodgerblue',alpha=0.5, s=60, zorder=2)
mp.plot(dates, trend_line, linestyle='o-', c='dodgerblue',linewidth=3, label='Trend')
mp.legend()
mp.gcf().autofmt_xdate()
mp.show()

绘制顶部压力线（趋势线+(最高价 - 最低价)）

trend_points = (highest_prices + lowest_prices + closing_prices) / 3
spreads = highest_prices - lowest_prices
resistance_points = trend_points + spreads
days = dates.astype(int)
x = np.linalg.lstsq(a, resistance_points)[0]
resistance_line = days * x[0] + x[1]
mp.scatter(dates, resistance_points, c='orangered', alpha=0.5, s=60, zorder=2)
mp.plot(dates, resistance_line, c='orangered', linewidth=3, label='Resistance')

绘制底部支撑线（趋势线-(最高价 - 最低价)）

trend_points = (highest_prices + lowest_prices + closing_prices) / 3
spreads = highest_prices - lowest_prices
support_points = trend_points - spreads
days = dates.astype(int)
x = np.linalg.lstsq(a, support_points)[0]
support_line = days * x[0] + x[1]
mp.scatter(dates, support_points, c='limegreen', alpha=0.5, s=60, zorder=2)
mp.plot(dates, support_line, c='limegreen', linewidth=3, label='Support')

协方差、相关矩阵、相关系数

通过两组统计数据计算而得的协方差可以评估这两组统计数据的相似程度。

样本：

A = [a1, a2, ..., an]
B = [b1, b2, ..., bn]

平均值：

ave_a = (a1 + a2 +...+ an)/n
ave_b = (b1 + b2 +...+ bn)/m

离差（用样本中的每一个元素减去平均数，求得数据的误差程度）：

dev_a = [a1, a2, ..., an] - ave_a
dev_b = [b1, b2, ..., bn] - ave_b

协方差

协方差可以简单反映两组统计样本的相关性，值为正，则为正相关；值为负，则为负相关，绝对值越大相关性越强。

cov_ab = ave(dev_a x dev_b)
cov_ba = ave(dev_b x dev_a)

案例：计算两组数据的协方差，并绘图观察。

import numpy as np
import matplotlib.pyplot as mp

a = np.random.randint(1, 30, 10)
b = np.random.randint(1, 30, 10)
#平均值
ave_a = np.mean(a)
ave_b = np.mean(b)
#离差
dev_a = a - ave_a
dev_b = b - ave_b
#协方差
cov_ab = np.mean(dev_a*dev_b)
cov_ba = np.mean(dev_b*dev_a)
print('a与b数组：', a, b)
print('a与b样本方差：', np.sum(dev_a**2)/(len(dev_a)-1), np.sum(dev_b**2)/(len(dev_b)-1))
print('a与b协方差：',cov_ab, cov_ba)
#绘图，查看两条图线的相关性
mp.figure('COV LINES', facecolor='lightgray')
mp.title('COV LINES', fontsize=16)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
x = np.arange(0, 10)
#a,b两条线
mp.plot(x, a, color='dodgerblue', label='Line1')
mp.plot(x, b, color='limegreen', label='Line2')
#a,b两条线的平均线
mp.plot([0, 9], [ave_a, ave_a], color='dodgerblue', linestyle='--', alpha=0.7, linewidth=3)
mp.plot([0, 9], [ave_b, ave_b], color='limegreen', linestyle='--', alpha=0.7, linewidth=3)

mp.grid(linestyle='--', alpha=0.5)
mp.legend()
mp.tight_layout()
mp.show()

相关系数

协方差除去两组统计样本的乘积是一个[-1, 1]之间的数。该结果称为统计样本的相关系数。

# a组样本 与 b组样本做对照后的相关系数
cov_ab/(std_a x std_b)
# b组样本 与 a组样本做对照后的相关系数
cov_ba/(std_b x std_a)
# a样本与a样本作对照   b样本与b样本做对照   二者必然相等
cov_ab/(std_a x std_b)=cov_ba/(std_b x std_a)

通过相关系数可以分析两组数据的相关性：

若相关系数越接近于0，越表示两组样本越不相关。
若相关系数越接近于1，越表示两组样本正相关。
若相关系数越接近于-1，越表示两组样本负相关。

案例：输出案例中两组数据的相关系数。

print('相关系数：', cov_ab/(np.std(a)*np.std(b)), cov_ba/(np.std(a)*np.std(b)))

相关矩阵

$frac{var_a}{std_a times std_a} & frac{cov_ab}{std_a times std_b} \ frac{cov_ba}{std_b times std_a} & frac{var_b}{std_b times std_b}\ end{array} right ]$
矩阵正对角线上的值都为1。（同组样本自己相比绝对正相关）
$frac{cov_ab}{std_a times std_b} \ frac{cov_ba}{std_b times std_a} & 1\ end{array} right ]$
numpy提供了求得相关矩阵的API：

# 相关矩阵
numpy.corrcoef(a, b)	
# 相关矩阵的分子矩阵 
# [[a方差，ab协方差], [ba协方差, b方差]]
numpy.cov(a, b)

多项式拟合

多项式的一般形式：
$y=p_{0}x^n + p_{1}x^{n-1} + p_{2}x^{n-2} + p_{3}x^{n-3} +...+p_{n}$
多项式拟合的目的是为了找到一组p0-pn，使得拟合方程尽可能的与实际样本数据相符合。

假设拟合得到的多项式如下：
$f(x)=p_{0}x^n + p_{1}x^{n-1} + p_{2}x^{n-2} + p_{3}x^{n-3} +...+p_{n}$
则拟合函数与真实结果的差方如下
$loss = (y_1-f(x_1))^2 + (y_2-f(x_2))^2 + ... + (y_n-f(x_n))^2$
那么多项式拟合的过程即为求取一组p₀-p_n,使得loss的值最小。

X = [x1, x2, ..., xn] - 自变量
Y = [y1, y2, ..., yn] - 实际函数值
Y'= [y1',y2',...,yn'] - 拟合函数值
P = [p0, p1, ..., pn] - 多项式函数中的系数

根据一组样本，并给出最高次幂，求出拟合系数
np.polyfit(X, Y, 最高次幂)->P

多项式运算相关API：

根据拟合系数与自变量求出拟合值, 由此可得拟合曲线坐标样本数据 [X, Y']
np.polyval(P, X)->Y'

多项式函数求导，根据拟合系数求出多项式函数导函数的系数
np.polyder(P)->Q 

已知多项式系数Q 求多项式函数的根（与x轴交点的横坐标）
xs = np.roots(Q)

两个多项式函数的差函数的系数（可以通过差函数的根求取两个曲线的交点）
Q = np.polysub(P1, P2)

案例：求多项式 y = 4x³ + 3x² - 1000x + 1曲线拐点的坐标。

'''
1. 求出多项式的导函数
2. 求出导函数的根，若导函数的根为实数，则该点则为曲线拐点。
'''
import numpy as np
import matplotlib.pyplot as mp

x = np.linspace(-20, 20, 1000)
y = 4*x**3 + 3*x**2  - 1000*x + 1
Q = np.polyder([4,3,-1000,1])
xs = np.roots(Q)
ys =  4*xs**3 + 3*xs**2  - 1000*xs + 1
mp.plot(x, y)
mp.scatter(xs, ys, s=80, c='orangered')
mp.show()

案例：使用多项式函数拟合两只股票bhp、vale的差价函数：

'''
1. 计算两只股票的差价
2. 利用多项式拟合求出与两只股票差价相近的多项式系数，最高次为4
3. 把该曲线的拐点都标出来。
'''
dates, bhp_closing_prices = np.loadtxt('../../data/bhp.csv', 
                                       delimiter=',',usecols=(1, 6), unpack=True, 
                                       dtype='M8[D], f8', conv erters={1: dmy2ymd})
vale_closing_prices = np.loa dtxt('../../data/vale.csv', delimiter=',',
                                 usecols=(6), unpack=True)
diff_closing_prices = bhp_closing_prices - vale_closing_prices
days = dates.astype(int)
p = np.polyfit(days, diff_closing_prices, 4)
poly_closing_prices = np.polyval(p, days)
q = np.polyder(p)
roots_x = np.roots(q)
roots_y = np.polyval(p, roots_x)
mp.figure('Polynomial Fitting', facecolor='lightgray')
mp.title('Polynomial Fitting', fontsize=20)
mp.xlabel('Date', fontsize=14)
mp.ylabel('Difference Price', fontsize=14)
ax = mp.gca()
ax.xaxis.set_major_locator(md.WeekdayLocator(byweekday=md.MO))
ax.xaxis.set_minor_locator(md.DayLocator())
ax.xaxis.set_major_formatter(md.DateFormatter('%d %b %Y'))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
dates = dates.astype(md.datetime.datetime)
mp.plot(dates, poly_closing_prices, c='limegreen',
        linewidth=3, label='Polynomial Fitting')
mp.scatter(dates, diff_closing_prices, c='dodgerblue',
           alpha=0.5, s=60, label='Difference Price')
roots_x = roots_x.astype(int).astype('M8[D]').astype(
    		md.datetime.datetime)
mp.scatter(roots_x, roots_y, marker='^', s=80,
           c='orangered', label='Peek', zorder=4)
mp.legend()
mp.gcf().autofmt_xdate()
mp.show()

数据平滑

数据的平滑处理通常包含有降噪、拟合等操作。降噪的功能意在去除额外的影响因素，拟合的目的意在数学模型化，可以通过更多的数学方法识别曲线特征。

案例：绘制两只股票收益率曲线。收益率 =（后一天收盘价-前一天收盘价） / 前一天收盘价

使用卷积完成数据降噪。

dates, bhp_closing_prices = np.loadtxt( '../data/bhp.csv', delimiter=',', usecols=(1,6), dtype='M8[D], f8',converters={1:dmy2ymd}, unpack=True)
vale_closing_prices = np.loadtxt( '../data/vale.csv', delimiter=',', usecols=(6), dtype='f8',converters={1:dmy2ymd}, unpack=True)

bhp_returns = np.diff(bhp_closing_prices) / bhp_closing_prices[:-1]
vale_returns = np.diff(vale_closing_prices) / vale_closing_prices[:-1]
dates = dates[:-1]

#卷积降噪
convolve_core = np.hanning(8)
convolve_core /= convolve_core.sum()
bhp_returns_convolved = np.convolve(bhp_returns, convolve_core, 'valid')
vale_returns_convolved = np.convolve(vale_returns, convolve_core, 'valid')
#绘制这条曲线
mp.figure('BHP VALE RETURNS', facecolor='lightgray')
mp.title('BHP VALE RETURNS', fontsize=20)
mp.xlabel('Date')
mp.ylabel('Price')
ax = mp.gca()
ax.xaxis.set_major_locator(md.WeekdayLocator(byweekday=md.MO))
ax.xaxis.set_minor_locator(md.DayLocator())
ax.xaxis.set_major_formatter(md.DateFormatter('%Y %m %d'))
dates = dates.astype('M8[D]')
#绘制收益线
mp.plot(dates, bhp_returns, color='dodgerblue', linestyle='--', label='bhp_returns', alpha=0.3)
mp.plot(dates, vale_returns, color='orangered', linestyle='--', label='vale_returns', alpha=0.3)
#绘制卷积降噪线
mp.plot(dates[7:], bhp_returns_convolved, color='dodgerblue', label='bhp_returns_convolved', alpha=0.5)
mp.plot(dates[7:], vale_returns_convolved, color='orangered', label='vale_returns_convolved', alpha=0.5)

mp.show()

对处理过的股票收益率做多项式拟合。

#拟合这两条曲线，获取两组多项式系数
dates = dates.astype(int)
bhp_p = np.polyfit(dates[7:], bhp_returns_convolved, 3)
bhp_polyfit_y = np.polyval(bhp_p, dates[7:])
vale_p = np.polyfit(dates[7:], vale_returns_convolved, 3)
vale_polyfit_y = np.polyval(vale_p, dates[7:])
#绘制拟合线
mp.plot(dates[7:], bhp_polyfit_y, color='dodgerblue', label='bhp_returns_polyfit')
mp.plot(dates[7:], vale_polyfit_y, color='orangered', label='vale_returns_polyfit')

通过获取两个函数的焦点可以分析两只股票的投资收益比。

#求两条曲线的交点  f(bhp) = f(vale)的根
sub_p = np.polysub(bhp_p, vale_p)
roots_x = np.roots(sub_p)	# 让f(bhp) - f(vale) = 0  函数的两个根既是两个函数的焦点
roots_x = roots_x.compress( (dates[0] <= roots_x) & (roots_x <= dates[-1]))
roots_y = np.polyval(bhp_p, roots_x)
#绘制这些点
mp.scatter(roots_x, roots_y, marker='D', color='green', s=60, zorder=3)

符号数组

sign函数可以把样本数组的变成对应的符号数组，正数变为1，负数变为-1，0则变为0。

ary = np.sign(源数组)

净额成交量（OBV）

成交量可以反映市场对某支股票的人气，而成交量是一只股票上涨的能量。一支股票的上涨往往需要较大的成交量。而下跌时则不然。

若相比上一天的收盘价上涨，则为正成交量；若相比上一天的收盘价下跌，则为负成交量。

绘制OBV柱状图

dates, closing_prices, volumes = np.loadtxt(
    '../../data/bhp.csv', delimiter=',',
    usecols=(1, 6, 7), unpack=True,
    dtype='M8[D], f8, f8', converters={1: dmy2ymd})
diff_closing_prices = np.diff(closing_prices)
sign_closing_prices = np.sign(diff_closing_prices)
obvs = volumes[1:] * sign_closing_prices
mp.figure('On-Balance Volume', facecolor='lightgray')
mp.title('On-Balance Volume', fontsize=20)
mp.xlabel('Date', fontsize=14)
mp.ylabel('OBV', fontsize=14)
ax = mp.gca()
ax.xaxis.set_major_locator(md.WeekdayLocator(byweekday=md.MO))
ax.xaxis.set_minor_locator(md.DayLocator())
ax.xaxis.set_major_formatter(md.DateFormatter('%d %b %Y'))
mp.tick_params(labelsize=10)
mp.grid(axis='y', linestyle=':')
dates = dates[1:].astype(md.datetime.datetime)
mp.bar(dates, obvs, 1.0, color='dodgerblue',
       edgecolor='white', label='OBV')
mp.legend()
mp.gcf().autofmt_xdate()
mp.show()

数组处理函数

ary = np.piecewise(源数组, 条件序列, 取值序列)

针对源数组中的每一个元素，检测其是否符合条件序列中的每一个条件，符合哪个条件就用取值系列中与之对应的值，表示该元素，放到目标数组中返回。

条件序列: [a < 0, a == 0, a > 0]

取值序列: [-1, 0, 1]

a = np.array([70, 80, 60, 30, 40])
d = np.piecewise(
    a, 
    [a < 60, a == 60, a > 60],
    [-1, 0, 1])
# d = [ 1  1  0 -1 -1]

矢量化

矢量化指的是用数组代替标量来操作数组里的每个元素。

numpy提供了vectorize函数，可以把处理标量的函数矢量化，返回的函数可以直接处理ndarray数组。

import math as m
import numpy as np

def foo(x, y):
    return m.sqrt(x**2 + y**2)

x, y = 1, 4
print(foo(x, y))
X, Y = np.array([1, 2, 3]), np.array([4, 5, 6])
vectorized_foo = np.vectorize(foo)
print(vectorized_foo(X, Y))
print(np.vectorize(foo)(X, Y))

numpy还提供了frompyfuc函数，也可以完成与vectorize相同的功能：

# 把foo转换成矢量函数，该矢量函数接收2个参数，返回一个结果 
fun = np.frompyfunc(foo, 2, 1)
fun(X, Y)

案例：定义一种买进卖出策略，通过历史数据判断这种策略是否值得实施。

dates, opening_prices, highest_prices, 
    lowest_prices, closing_prices = np.loadtxt(
        '../../data/bhp.csv', delimiter=',',
        usecols=(1, 3, 4, 5, 6), unpack=True,
        dtype='M8[D], f8, f8, f8, f8',
        converters={1: dmy2ymd})
    
# 定义一种投资策略
def profit(opening_price, highest_price,
           lowest_price, closing_price):
    buying_price = opening_price * 0.99
    if lowest_price <= buying_price <= highest_price:
        return (closing_price - buying_price) * 
            100 / buying_price
    return np.nan  # 无效值

# 矢量化投资函数
profits = np.vectorize(profit)(opening_prices, 
       highest_prices, lowest_prices, closing_prices)
nan = np.isnan(profits)
dates, profits = dates[~nan], profits[~nan]
gain_dates, gain_profits = dates[profits > 0], profits[profits > 0]
loss_dates, loss_profits = dates[profits < 0], profits[profits < 0]
mp.figure('Trading Simulation', facecolor='lightgray')
mp.title('Trading Simulation', fontsize=20)
mp.xlabel('Date', fontsize=14)
mp.ylabel('Profit', fontsize=14)
ax = mp.gca()
ax.xaxis.set_major_locator(md.WeekdayLocator(byweekday=md.MO))
ax.xaxis.set_minor_locator(md.DayLocator())
ax.xaxis.set_major_formatter(md.DateFormatter('%d %b %Y'))
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
if dates.size > 0:
    dates = dates.astype(md.datetime.datetime)
    mp.plot(dates, profits, c='gray',
            label='Profit')
    mp.axhline(y=profits.mean(), linestyle='--',
               color='gray')
if gain_dates.size > 0:
    gain_dates = gain_dates.astype(md.datetime.datetime)
    mp.plot(gain_dates, gain_profits, 'o',
            c='orangered', label='Gain Profit')
    mp.axhline(y=gain_profits.mean(), linestyle='--',
               color='orangered')
if loss_dates.size > 0:
    loss_dates = loss_dates.astype(md.datetime.datetime)
    mp.plot(loss_dates, loss_profits, 'o',
            c='limegreen', label='Loss Profit')
    mp.axhline(y=loss_profits.mean(), linestyle='--',
               color='limegreen')
mp.legend()
mp.gcf().autofmt_xdate()
mp.show()

矩阵

矩阵是numpy.matrix类类型的对象，该类继承自numpy.ndarray，任何针对多维数组的操作，对矩阵同样有效，但是作为子类矩阵又结合其自身的特点，做了必要的扩充，比如：乘法计算、求逆等。

矩阵对象的创建

# 如果copy的值为True(缺省)，所得到的矩阵对象与参数中的源容器共享同一份数
# 据，否则，各自拥有独立的数据拷贝。
numpy.matrix(
    ary,		# 任何可被解释为矩阵的二维容器
  	copy=True	# 是否复制数据(缺省值为True，即复制数据)
)

# 等价于：numpy.matrix(..., copy=False)
# 由该函数创建的矩阵对象与参数中的源容器一定共享数据，无法拥有独立的数据拷贝
numpy.mat(任何可被解释为矩阵的二维容器)

# 该函数可以接受字符串形式的矩阵描述：
# 数据项通过空格分隔，数据行通过分号分隔。例如：'1 2 3; 4 5 6'
numpy.mat(拼块规则)

矩阵的乘法运算

# 矩阵的乘法：乘积矩阵的第i行第j列的元素等于
# 被乘数矩阵的第i行与乘数矩阵的第j列的点积
#
#           1   2   6
#    X----> 3   5   7
#    |      4   8   9
#    |
# 1  2  6   31  60  74
# 3  5  7   46  87 116
# 4  8  9   64 120 161
e = np.mat('1 2 6; 3 5 7; 4 8 9')
print(e * e)

矩阵的逆矩阵

若两个矩阵A、B满足：AB = BA = E （E为单位矩阵），则成为A、B为逆矩阵。

e = np.mat('1 2 6; 3 5 7; 4 8 9')
print(e.I)
print(e * e.I)

ndarray提供了方法让多维数组替代矩阵的运算：

a = np.array([
    [1, 2, 6],
    [3, 5, 7],
    [4, 8, 9]])
# 点乘法求ndarray的点乘结果，与矩阵的乘法运算结果相同
k = a.dot(a)
print(k)
# linalg模块中的inv方法可以求取a的逆矩阵
l = np.linalg.inv(a)
print(l)

案例：假设一帮孩子和家长出去旅游，去程坐的是bus，小孩票价为3元，家长票价为3.2元，共花了118.4；回程坐的是Train，小孩票价为3.5元，家长票价为3.6元，共花了135.2。分别求小孩和家长的人数。使用矩阵求解。
$$
left[ begin{array}{ccc}
3 & 3.2
3.5 & 3.6
end{array} right]
times
left[ begin{array}{ccc}
x
y
end{array} right]

left[ begin{array}{ccc}
118.4
135.2
end{array} right]
$$

import numpy as np

prices = np.mat('3 3.2; 3.5 3.6')
totals = np.mat('118.4; 135.2')

persons = prices.I * totals
print(persons)

案例：斐波那契数列

1 1 2 3 5 8 13 21 34 …

X      1   1    1   1    1   1
       1   0    1   0    1   0
    --------------------------------
1  1   2   1    3   2    5   3
1  0   1   1    2   1    3   2
 F^1    F^2      F^3 	  F^4  ...  f^n

代码

import numpy as np
n = 35

# 使用递归实现斐波那契数列
def fibo(n):
    return 1 if n < 3 else fibo(n - 1) + fibo(n - 2)
print(fibo(n))

# 使用矩阵实现斐波那契数列
print(int((np.mat('1. 1.; 1. 0.') ** (n - 1))[0, 0]))

通用函数

数组的裁剪

# 将调用数组中小于和大于下限和上限的元素替换为下限和上限，返回裁剪后的数组，调
# 用数组保持不变。
ndarray.clip(min=下限, max=上限)

数组的压缩

# 返回由调用数组中满足条件的元素组成的新数组。
ndarray.compress(条件)

数组的累乘

# 返回调用数组中所有元素的乘积——累乘。
ndarray.prod()
# 返回调用数组中所有元素执行累乘的过程数组。
ndarray.cumprod()

案例：

from __future__ import unicode_literals
import numpy as np
a = np.array([10, 20, 30, 40, 50])
print(a)
b = a.clip(min=15, max=45)
print(b)
c = a.compress((15 <= a) & (a <= 45))
print(c)
d = a.prod()
print(d)
e = a.cumprod()
print(e)

def jiecheng(n):
    return n if n == 1 else n * jiecheng(n - 1)

n = 5
print(jiecheng(n))
jc = 1
for i in range(2, n + 1):
    jc *= i
print(jc)
print(np.arange(2, n + 1).prod())

加法通用函数

add(a, a) 					# 两数组相加
add.reduce(a) 				# a数组元素累加和
add.accumulate(a) 			# 累加和过程
add.outer([10, 20, 30], a)	# 外和

案例：

a = np.arange(1, 7)
print(a)
b = a + a
print(b)
b = np.add(a, a)
print(b)
c = np.add.reduce(a)
print(c)
d = np.add.accumulate(a)
print(d)
#  +  	 1  2  3  4  5  6   
#	   --------------------
# 10   |11 12 13 14 15 16 |
# 20   |21 22 23 24 25 26 |
# 30   |31 32 33 34 35 36 |
       --------------------
f = np.add.outer([10, 20, 30], a)
print(f)
#  x  	 1  2  3  4  5  6   
#	   -----------------------
# 10   |10 20 30  40  50  60 |
# 20   |20 40 60  80 100 120 |
# 30   |30 60 90 120 150 180 |
       -----------------------
g = np.outer([10, 20, 30], a)
print(g)

除法通用函数

np.true_divide(a, b) 	# a 真除 b  （对应位置相除）
np.divide(a, b) 		# a 真除 b
np.floor_divide(a, b)	# a 地板除 b	（真除的结果向下取整）
np.ceil(a / b) 		# a 天花板除 b	（真除的结果向上取整）
np.trunc(a / b)			# a 截断除 b	（真除的结果直接干掉小数部分）

案例：

import numpy as np

a = np.array([20, 20, -20, -20])
b = np.array([3, -3, 6, -6])
# 真除
c = np.true_divide(a, b)
c = np.divide(a, b)
c = a / b
print('array:',c)
# 对ndarray做floor操作
d = np.floor(a / b)
print('floor_divide:',d)
# 对ndarray做ceil操作
e = np.ceil(a / b)
print('ceil ndarray:',e)
# 对ndarray做trunc操作
f = np.trunc(a / b)
print('trunc ndarray:',f)
# 对ndarray做around操作
g = np.around(a / b)
print('around ndarray:',g)

三角函数通用函数

numpy.sin()

合成方波

一个方波由如下参数的正弦波叠加而成：
$\ y = frac{4pi}{3} times sin(3x) \ ...\ ...\ y = frac{4pi}{2n-1} times sin((2n-1)x)$
曲线叠加的越多，越接近方波。所以可以设计一个函数，接收曲线的数量n作为参数，返回一个矢量函数，该函数可以接收x坐标数组，返回n个正弦波叠加得到的y坐标数组。

x = np.linspace(-2*np.pi, 2*np.pi, 1000)
y = np.zeros(1000)
n = 1000
for i in range(1， n+1):
	y += 4 / ((2 * i - 1) * np.pi) * np.sin((2 * i - 1) * x)
mp.plot(x, y, label='n=1000')
mp.legend()
mp.show()

位运算通用函数

位异或：

c = a ^ b
c = a.__xor__(b)
c = np.bitwise_xor(a, b)

按位异或操作可以很方便的判断两个数据是否同号。

0 ^ 0 = 0
0 ^ 1 = 1
1 ^ 0 = 1
1 ^ 1 = 0

a = np.array([0, -1, 2, -3, 4, -5])
b = np.array([0, 1, 2, 3, 4, 5])
print(a, b)
c = a ^ b
# c = a.__xor__(b)
# c = np.bitwise_xor(a, b)
print(np.where(c < 0)[0])

位与：

e = a & b
e = a.__and__(b)
e = np.bitwise_and(a, b)

利用位与运算计算某个数字是否是2的幂

#  1 2^0 00001   0 00000
#  2 2^1 00010   1 00001
#  4 2^2 00100   3 00011
#  8 2^3 01000   7 00111
# 16 2^4 10000  15 01111
# ...

d = np.arange(1, 21)
print(d)
e = d & (d - 1)
e = d.__and__(d - 1)
e = np.bitwise_and(d, d - 1)
print(e)

位或：

|
__or__
bitwise_or

0 | 0 = 0
0 | 1 = 1
1 | 0 = 1
1 | 1 = 1
位反：

~
__not__
bitwise_not

~0 = 1
~1 = 0
移位：

<<		__lshift__		left_shift
>>		__rshift__		right_shift

左移1位相当于乘2，右移1位相当于除2。

d = np.arange(1, 21)
print(d)
# f = d << 1
# f = d.__lshift__(1)
f = np.left_shift(d, 1)
print(f)

特征值和特征向量

对于n阶方阵A，如果存在数a和非零n维列向量x，使得Ax=ax，则称a是矩阵A的一个特征值，x是矩阵A属于特征值a的特征向量

#已知n阶方阵A， 求特征值与特征数组
# eigvals: 特征值数组
# eigvecs: 特征向量数组 
eigvals, eigvecs = np.linalg.eig(A)
#已知特征值与特征向量，求方阵
S = np.mat(eigvecs) * np.mat(np.diag(eigvals)) * np.mat(eigvecs逆)

案例：

import numpy as np
A = np.mat('3 -2; 1 0')
print(A)
eigvals, eigvecs = np.linalg.eig(A)
print(eigvals)
print(eigvecs)
print(A * eigvecs[:, 0])	# 方阵*特征向量
print(eigvals[0] * eigvecs[:, 0])	#特征值*特征向量
S = np.mat(eigvecs) * np.mat(np.diag(eigvals)) * np.mat(eigvecs.I)

案例：读取图片的亮度矩阵，提取特征值与特征向量，保留部分特征值，重新生成新的亮度矩阵，绘制图片。

'''
特征值与特征向量
'''
import numpy as np
import scipy.misc as sm
import matplotlib.pyplot as mp


original = sm.imread('../data/lily.jpg', True)
#提取特征值
eigvals, eigvecs = np.linalg.eig(original)
eigvals[50:] = 0
print(np.diag(eigvals).shape)
original2 = np.mat(eigvecs) * np.mat(np.diag(eigvals)) * np.mat(eigvecs).I
mp.figure("Lily Features")
mp.subplot(121)
mp.xticks([])
mp.yticks([])
mp.imshow(original, cmap='gray')

mp.subplot(122)
mp.xticks([])
mp.yticks([])
mp.imshow(original2, cmap='gray')
mp.tight_layout()
mp.show()

奇异值分解

有一个矩阵M，可以分解为3个矩阵U、S、V，使得U x S x V等于M。U与V都是正交矩阵（乘以自身的转置矩阵结果为单位矩阵）。那么S矩阵主对角线上的元素称为矩阵M的奇异值，其它元素均为0。

import numpy as np
M = np.mat('4 11 14; 8 7 -2')
print(M)
U, sv, V = np.linalg.svd(M, full_matrices=False)
print(U * U.T)
print(V * V.T)
print(sv)
S = np.diag(sv)
print(S)
print(U * S * V)

案例：读取图片的亮度矩阵，提取奇异值与两个正交矩阵，保留部分奇异值，重新生成新的亮度矩阵，绘制图片。

original = sm.imread('../data/lily.jpg', True)
#提取奇异值  sv 	
U, sv, V = np.linalg.svd(original)
print(U.shape, sv.shape, V.shape)
sv[50:] = 0
original2 = np.mat(U) * np.mat(np.diag(sv)) * np.mat(V)
mp.figure("Lily Features")
mp.subplot(221)
mp.xticks([])
mp.yticks([])
mp.imshow(original, cmap='gray')

mp.subplot(222)
mp.xticks([])
mp.yticks([])
mp.imshow(original2, cmap='gray')
mp.tight_layout()

快速傅里叶变换模块(fft)

什么是傅里叶变换？

法国科学家傅里叶提出，任何一条周期曲线，无论多么跳跃或不规则，都能表示成一组光滑正弦曲线叠加之和。

傅里叶变换的目的是可将时域（即时间域）上的信号转变为频域（即频率域）上的信号，随着域的不同，对同一个事物的了解角度也就随之改变，因此在时域中某些不好处理的地方，在频域就可以较为简单的处理。这就可以大量减少处理信号存储量。

例如：弹钢琴

假设有一时间域函数：y = f(x)，根据傅里叶的理论它可以被分解为一系列正弦函数的叠加，他们的振幅A，频率ω或初相位φ不同：
$A_1sin(omega_1x+phi_1) + A_2sin(omega_2x+phi_2) + A_2sin(omega_2x+phi_2) + R$
所以傅里叶变换可以把一个比较复杂的函数转换为多个简单函数的叠加，看问题的角度也从时间域转到了频率域，有些的问题处理起来就会比较简单。

傅里叶变换相关函数

导入快速傅里叶变换所需模块

import numpy.fft as nf

通过采样数与采样周期求得傅里叶变换分解所得曲线的频率序列

freqs = np.fft.fftfreq(采样数量, 采样周期)

通过原函数值的序列j经过快速傅里叶变换得到一个复数数组，复数的模代表的是振幅，复数的辐角代表初相位

np.fft.fft(原函数值序列) -> 目标函数值序列(复数)

通过一个复数数组（复数的模代表的是振幅，复数的辐角代表初相位）经过逆向傅里叶变换得到合成的函数值数组

np.fft.ifft(目标函数值序列(复数))->原函数值序列

案例：针对合成波做快速傅里叶变换，得到一组复数序列；再针对该复数序列做逆向傅里叶变换得到新的合成波并绘制。

ffts = nf.fft(sigs6)
sigs7 = nf.ifft(ffts).real
mp.plot(times, sigs7, label=r'$omega$='+str(round(1 / (2 * np.pi),3)), alpha=0.5, linewidth=6)

案例：针对合成波做快速傅里叶变换，得到分解波数组的频率、振幅、初相位数组，并绘制频域图像。

# 得到分解波的频率序列
freqs = nf.fftfreq(times.size, times[1] - times[0])
# 复数的模为信号的振幅（能量大小）
ffts = nf.fft(sigs6)
pows = np.abs(ffts)

mp.subplot(122)
mp.title('Frequency Domain', fontsize=16)
mp.xlabel('Frequency', fontsize=12)
mp.ylabel('Power', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(freqs[freqs >= 0], pows[freqs >= 0], c='orangered', label='Frequency Spectrum')
mp.legend()
mp.tight_layout()
mp.show()

基于傅里叶变换的频域滤波

含噪信号是高能信号与低能噪声叠加的信号，可以通过傅里叶变换的频域滤波实现降噪。

通过FFT使含噪信号转换为含噪频谱，去除低能噪声，留下高能频谱后再通过IFFT留下高能信号。

案例：基于傅里叶变换的频域滤波为音频文件去除噪声。

读取音频文件，获取音频文件基本信息：采样个数，采样周期，与每个采样的声音信号值。绘制音频时域的：时间/位移图像。

import numpy as np
import numpy.fft as nf
import scipy.io.wavfile as wf
import matplotlib.pyplot as mp

sample_rate, noised_sigs = wf.read('../data/noised.wav')
noised_sigs = noised_sigs / 2 ** 15
times = np.arange(len(noised_sigs)) / sample_rate
mp.figure('Filter', facecolor='lightgray')
mp.subplot(221)
mp.title('Time Domain', fontsize=16)
mp.ylabel('Signal', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(times[:178], noised_sigs[:178],c='orangered', label='Noised')
mp.legend()
mp.show()

基于傅里叶变换，获取音频频域信息，绘制音频频域的：频率/能量图像。

freqs = nf.fftfreq(times.size, 1 / sample_rate)
noised_ffts = nf.fft(noised_sigs)
noised_pows = np.abs(noised_ffts)
mp.subplot(222)
mp.title('Frequency Domain', fontsize=16)
mp.ylabel('Power', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.semilogy(freqs[freqs >= 0],noised_pows[freqs >= 0], c='limegreen',label='Noised')
mp.legend()

将低频噪声去除后绘制音频频域的：频率/能量图像。

fund_freq = freqs[noised_pows.argmax()]
noised_indices = np.where(freqs != fund_freq)
filter_ffts = noised_ffts.copy()
filter_ffts[noised_indices] = 0
filter_pows = np.abs(filter_ffts)

mp.subplot(224)
mp.xlabel('Frequency', fontsize=12)
mp.ylabel('Power', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(freqs[freqs >= 0], filter_pows[freqs >= 0],c='dodgerblue', label='Filter')
mp.legend()

基于逆向傅里叶变换，生成新的音频信号，绘制音频时域的：时间/位移图像。

filter_sigs = nf.ifft(filter_ffts).real
mp.subplot(223)
mp.xlabel('Time', fontsize=12)
mp.ylabel('Signal', fontsize=12)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(times[:178], filter_sigs[:178],c='hotpink', label='Filter')
mp.legend()

重新生成音频文件。

wf.write('../../data/filter.wav',sample_rate,(filter_sigs * 2 ** 15).astype(np.int16))

随机数模块(random)

生成服从特定统计规律的随机数序列。

二项分布（binomial）

二项分布就是重复n次独立事件的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，事件发生与否的概率在每一次独立试验中都保持不变。

# 产生size个随机数，每个随机数来自n次尝试中的成功次数，其中每次尝试成功的概率为p。
np.random.binomial(n, p, size)

二项分布可以用于求如下场景的概率的近似值：

某人投篮命中率为0.3，投10次，进5个球的概率。

sum(np.random.binomial(10, 0.3, 200000) == 5) / 200000

某人打客服电话，客服接通率是0.6，一共打了3次，都没人接的概率。

sum(np.random.binomial(3, 0.6, 200000) == 0) / 200000

超几何分布(hypergeometric)

# 产生size个随机数，每个随机数t为在总样本中随机抽取nsample个样本后好样本的个数，总样本由ngood个好样本和nbad个坏样本组成
np.random.hypergeometric(ngood, nbad, nsample, size)

正态分布(normal)

# 产生size个随机数，服从标准正态(期望=0, 标准差=1)分布。
np.random.normal(size)
# 产生size个随机数，服从正态分布(期望=1, 标准差=10)。
np.random.normal(loc=1, scale=10, size)

$frac{e^{-frac{x^2}{2}}}{sqrt{2pi}}$

杂项功能

排序

联合间接排序

联合间接排序支持为待排序列排序，若待排序列值相同，则利用参考序列作为参考继续排序。最终返回排序过后的有序索引序列。

indices = numpy.lexsort((参考序列, 待排序列))

案例：先按价格排序，再按销售量倒序排列。

import numpy as np
prices = np.array([92,83,71,92,40,12,64])
volumes = np.array([100,251,4,12,709,34,75])
print(volumes)
names = ['Product1','Product2','Product3','Product4','Product5','Product6','Product7']
ind = np.lexsort((volumes*-1, prices)) 
print(ind)
for i in ind:
	print(names[i], end=' ')

复数数组排序

按照实部的升序排列，对于实部相同的元素，参考虚部的升序，直接返回排序后的结果数组。

numpy.sort_complex(复数数组)

插入排序

若有需求需要向有序数组中插入元素，使数组依然有序，numpy提供了searchsorted方法查询并返回可插入位置数组。

indices = numpy.searchsorted(有序序列, 待插序列)

调用numpy提供了insert方法将待插序列中的元素，按照位置序列中的位置，插入到被插序列中，返回插入后的结果。

numpy.insert(被插序列, 位置序列, 待插序列)

案例：

import numpy as np
#             0  1  2  3  4  5  6
a = np.array([1, 2, 4, 5, 6, 8, 9])
b = np.array([7, 3])
c = np.searchsorted(a, b)
print(c)
d = np.insert(a, c, b)
print(d)

插值

scipy提供了常见的插值算法可以通过一定规律插值器函数。若我们给插值器函数更多的散点x坐标序列，该函数将会返回相应的y坐标序列。

func = si.interp1d(
    离散水平坐标, 
    离散垂直坐标,
    kind=插值算法(缺省为线性插值)
)

案例：

# scipy.interpolate
import scipy.interpolate as si

# 原始数据 11组数据
min_x = -50
max_x = 50
dis_x = np.linspace(min_x, max_x, 11)
dis_y = np.sinc(dis_x)

# 通过一系列的散点设计出符合一定规律插值器函数，使用线性插值（kind缺省值）
linear = si.interp1d(dis_x, dis_y)
lin_x = np.linspace(min_x, max_x, 200)
lin_y = linear(lin_x)

# 三次样条插值 （CUbic Spline Interpolation） 获得一条光滑曲线
cubic = si.interp1d(dis_x, dis_y, kind='cubic')
cub_x = np.linspace(min_x, max_x, 200)
cub_y = cubic(cub_x)

积分

直观地说，对于一个给定的正实值函数，在一个实数区间上的定积分可以理解为坐标平面上由曲线、直线以及轴围成的曲边梯形的面积值（一种确定的实数值）。

利用微元法认识什么是积分。

案例：

在[-5, 5]区间绘制二次函数y=2x²+3x+4的曲线：

import numpy as np
import matplotlib.pyplot as mp
import matplotlib.patches as mc

def f(x):
    return 2 * x ** 2 + 3 * x + 4

a, b = -5, 5
x1 = np.linspace(a, b, 1001)
y1 = f(x1)
mp.figure('Integral', facecolor='lightgray')
mp.title('Integral', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.grid(linestyle=':')
mp.plot(x1, y1, c='orangered', linewidth=6,label=r'$y=2x^2+3x+4$', zorder=0)
mp.legend()
mp.show()

微分法绘制函数在与x轴还有[-5, 5]所组成的闭合区域中的小梯形。

n = 50
x2 = np.linspace(a, b, n + 1)
y2 = f(x2)
area = 0
for i in range(n):
    area += (y2[i] + y2[i + 1]) * (x2[i + 1] - x2[i]) / 2
print(area)
for i in range(n):
    mp.gca().add_patch(mc.Polygon([
        [x2[i], 0], [x2[i], y2[i]],
        [x2[i + 1], y2[i + 1]], [x2[i + 1], 0]],
        fc='deepskyblue', ec='dodgerblue',
        alpha=0.5))

调用scipy.integrate模块的quad方法计算积分：

import scipy.integrate as si
# 利用quad求积分 给出函数f，积分下限与积分上限[a, b]   返回(积分值，最大误差)
area = si.quad(f, a, b)[0]
print(area)

图像

scipy.ndimage中提供了一些简单的图像处理，如高斯模糊、任意角度旋转、边缘识别等功能。

import numpy as np
import scipy.misc as sm
import scipy.ndimage as sn
import matplotlib.pyplot as mp
#读取文件
original = sm.imread('../../data/head.jpg', True)
#高斯模糊
median = sn.median_filter(original, 21)
#角度旋转
rotate = sn.rotate(original, 45)
#边缘识别
prewitt = sn.prewitt(original)
mp.figure('Image', facecolor='lightgray')
mp.subplot(221)
mp.title('Original', fontsize=16)
mp.axis('off')
mp.imshow(original, cmap='gray')
mp.subplot(222)
mp.title('Median', fontsize=16)
mp.axis('off')
mp.imshow(median, cmap='gray')
mp.subplot(223)
mp.title('Rotate', fontsize=16)
mp.axis('off')
mp.imshow(rotate, cmap='gray')
mp.subplot(224)
mp.title('Prewitt', fontsize=16)
mp.axis('off')
mp.imshow(prewitt, cmap='gray')
mp.tight_layout()
mp.show()

金融相关

import numpy as np
# 终值 = np.fv(利率, 期数, 每期支付, 现值)
# 将1000元以1%的年利率存入银行5年，每年加存100元，
# 到期后本息合计多少钱？
fv = np.fv(0.01, 5, -100, -1000)
print(round(fv, 2))
# 现值 = np.pv(利率, 期数, 每期支付, 终值)
# 将多少钱以1%的年利率存入银行5年，每年加存100元，
# 到期后本息合计fv元？
pv = np.pv(0.01, 5, -100, fv)
print(pv)
# 净现值 = np.npv(利率, 现金流)
# 将1000元以1%的年利率存入银行5年，每年加存100元，
# 相当于一次性存入多少钱？
npv = np.npv(0.01, [
    -1000, -100, -100, -100, -100, -100])
print(round(npv, 2))
fv = np.fv(0.01, 5, 0, npv)
print(round(fv, 2))
# 内部收益率 = np.irr(现金流)
# 将1000元存入银行5年，以后逐年提现100元、200元、
# 300元、400元、500元，银行利率达到多少，可在最后
# 一次提现后偿清全部本息，即净现值为0元？
irr = np.irr([-1000, 100, 200, 300, 400, 500])
print(round(irr, 2))
npv = np.npv(irr, [-1000, 100, 200, 300, 400, 500])
print(npv)
# 每期支付 = np.pmt(利率, 期数, 现值)
# 以1%的年利率从银行贷款1000元，分5年还清，
# 平均每年还多少钱？
pmt = np.pmt(0.01, 5, 1000)
print(round(pmt, 2))
# 期数 = np.nper(利率, 每期支付, 现值)
# 以1%的年利率从银行贷款1000元，平均每年还pmt元，
# 多少年还清？
nper = np.nper(0.01, pmt, 1000)
print(int(nper))
# 利率 = np.rate(期数, 每期支付, 现值, 终值)
# 从银行贷款1000元，平均每年还pmt元，nper年还清，
# 年利率多少？
rate = np.rate(nper, pmt, 1000, 0)
print(round(rate, 2))

最后

以上就是闪闪过客为你收集整理的数据分析（学习笔记）$$ \left[ \begin{array}{ccc} x{_1} & 1\ x{_2} & 1\ x{_3} & 1 \ x{_n} & 1 \ \end{array} \right ] \times \left[ \begin{array}{ccc} k\ b\ \end{array} \right ]案例：假设一帮孩子和家长出去旅游，去程坐的是bus，小孩票价为3元，家长票价为3.2元，共花了118.4；回程坐的是Train，小孩票价为3.5元，家长票价为3.6元，共的全部内容，希望文章能够帮你解决数据分析（学习笔记）$$ \left[ \begin{array}{ccc} x{_1} & 1\ x{_2} & 1\ x{_3} & 1 \ x{_n} & 1 \ \end{array} \right ] \times \left[ \begin{array}{ccc} k\ b\ \end{array} \right ]案例：假设一帮孩子和家长出去旅游，去程坐的是bus，小孩票价为3元，家长票价为3.2元，共花了118.4；回程坐的是Train，小孩票价为3.5元，家长票价为3.6元，共所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：数据分析
浏览次数：81 次浏览
发布日期：2023-06-25 21:06:01
本文链接：https://www.kaopuke.com/article/k-p-k_14_uzo_26_f2_14_zc4.html

为什么研究数据可视化，以及研究到的东西

万字吐血好文，一线分析师的4大总结。一、分析师的商业价值二、业务不同阶段下数据分析的发力点与交付四、未来分析师所处的环境

数据分析报告：初级→高级，你没见过的写作指南！

优云软件数据专家最佳实践：数据挖掘与运维分析

$数据分析（学习笔记）$$ \left[ \begin{array}{ccc} x{_1} & 1\ x{_2} & 1\ x{_3} & 1 \ x{_n} & 1 \ \end{array} \right ] \times \left[ \begin{array}{ccc} k\ b\ \end{array} \right ]案例：假设一帮孩子和家长出去旅游，去程坐的是bus，小孩票价为3元，家长票价为3.2元，共花了118.4；回程坐的是Train，小孩票价为3.5元，家长票价为3.6元，共$

数据分析（学习笔记）$$ \left[ \begin{array}{ccc} x{_1} & 1\ x{_2} & 1\ x{_3} & 1 \ x{_n} & 1 \ \end{array} \right ] \times \left[ \begin{array}{ccc} k\ b\ \end{array} \right ]案例：假设一帮孩子和家长出去旅游，去程坐的是bus，小孩票价为3元，家长票价为3.2元，共花了118.4；回程坐的是Train，小孩票价为3.5元，家长票价为3.6元，共

概述

数据分析

numpy概述

numpy历史

numpy的核心：多维数组

numpy基础

ndarray数组

内存中的ndarray对象

ndarray数组对象的特点

ndarray数组对象的创建

ndarray对象属性的基本操作

ndarray对象属性操作详解

ndarray数组对象的维度操作

ndarray数组切片操作

ndarray数组的掩码操作

多维数组的组合与拆分

ndarray类的其他属性

matplotlib概述

matplotlib基本功能

matplotlib基本功能详解

基本绘图

绘图核心API

线型、线宽和颜色

设置坐标轴范围

设置坐标刻度

设置坐标轴

图例

特殊点

备注

图形对象（图形窗口）

子图

刻度定位器

刻度网格线

半对数坐标

散点图

填充

条形图（柱状图）

饼图

附录

matplotlib colors颜色字符串

matplotlib point样式

laTeX语法表示数学符号示例

LaTeX语法集合

cmap颜色映射表

等高线图

热成像图

极坐标系

3D图像绘制

简单动画

numpy常用函数

加载文件

算数平均值

加权平均值

numpy常用函数

最值

中位数

标准差

案例应用

时间数据处理

数组的轴向汇总

移动均线

卷积

布林带

线性模型

线性预测

线性拟合

$$ left[ begin{array}{ccc} x{_1} & 1 x{_2} & 1 x{_3} & 1 x{_n} & 1 end{array} right ] times left[ begin{array}{ccc} k b end{array} right ]

协方差、相关矩阵、相关系数

多项式拟合

数据平滑

符号数组

矢量化

矩阵

通用函数

加法通用函数

除法通用函数

三角函数通用函数

位运算通用函数

特征值和特征向量

奇异值分解

numpy`历史`

$$
left[ begin{array}{ccc}
x{_1} & 1
x{_2} & 1
x{_3} & 1
x{_n} & 1
end{array}
right ]
times
left[ begin{array}{ccc}
k
b
end{array}
right ]

发表评论取消回复