逻辑推理篇：数据分析最爱用的估算法：费米估计

在科学研究中，有这样一类估算问题，初次接触会觉得已知条件太少，无法得出答案，但如果对分析对象进行变通替换，问题就会迎刃而解，这就是费米问题。它可以用来对给定有限信息的问题做出清晰地验证估算。

一、费米估计的起源：

有这样的一个故事：1945年世界上第一颗原子弹爆炸。费米在感觉到震波的同时，把举过头顶的笔记本碎纸屑松开，碎纸屑落在身后2.5米的距离，通过心算后，得出结论原子弹的能量相当于10000tTNT的量，后来一些高科技仪器证明了费米的估算是正确的。

同样的故事还有：

地球的周长是多少？使用费米估计的解决方法是：已知纽约到洛杉矶3000英里，时差3小时，而一天即地球自转一周的时间为24小时，即3小时的8倍。所以，地球的周长就是3000乘以8，等于24000英里。与精确值的24902.45英里相比，误差不到4%。

芝加哥有多少钢琴调音师？使用费米估计的解决方法是： 如果芝加哥居民300万，平均每户4人，拥有钢琴的家庭占1/3，则全市有250000架钢琴。如果一架钢琴每5年调音一次，则全市每年有50000架钢琴要调音。如果一个调音师一天调4架钢琴，一年工作250天，那么，芝加哥市大约有50个调音师。

通过上面的例子，可以看出，直接通过非缜密计算可以快速把一个给定有限信息的费米难题转化成简单问题，进而快速得到解决，费米问题也因此受到人们的重视。

二、费米估计的原理

通过上面的案例，费米估计指的是解决少量信息的复杂估算问题，将复杂的问题拆解成常识性和已知的小问题，进而进行计算得到结果。所以解决问题的关键，主要有2个方面：

1.问题拆解

将未知的数逐步拆解成已知的部分，从而将一个未知结果的问题逐步变得清晰。问题拆解要按照一定的原则进行，比如使用MECE原则，做到不重不漏，复杂问题层层拆解为简单的子问题，从而解决问题。

在麦肯锡分析思维中，拆解问题的这种方法叫做议题树（也叫逻辑树或MECE原则），图下所示：

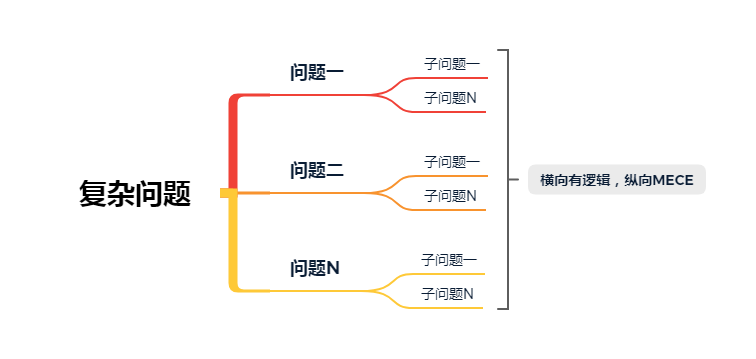
使用议题树对理清复杂问题的结构非常有帮助。

2.实际的常识数据准确

当我们拆解到实际子问题的时候，要确保实际常识代表的数据是有生活经验的支撑，而非凭空捏造的。

所以，我们可以总结出费米估计的一个具体步骤：

1. 首先，明确问题；

2. 按照MECE原则进行问题拆解；

3. 明确常识性已知数据；

4. 设计计算公式；

5. 计算，得出结果。

三、费米估计解决方法： Top-Down，Bottom-Up法则。

费米问题的解决，不仅需要有很强的思维逻辑，同时还需要广泛的常识性知识和准确数据的支持，非常锻炼一个人多方位的思考分析能力。在生活中实际用途也很多，比如预测行业趋势，估算市场份额，评估活动结果等。

解决费米问题的方法很多，比较典型的是Top-Down，Bottom-Up法则。

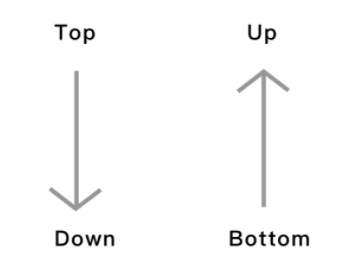
Top-Down，Bottom-Up法则的中心思想是：

首先，从2个方面展开拆解问题。一是自上而下，也就是纵向从宏观到微观直推；二是自下而上，横向从局部到全部反推。其次，对自上而下和自下而上的结果要进行对比，如果两者相减的绝对值在一个可接受的范围，那结果基本可以相信。最后，需要对可能产生误差的点进行补充，保证结果更加精确。

通俗的来说，自上而下和自下而上就是估算结果的两个边界，大的为上边界，小的为下边界，而最终的结果就落在两个边界里面了。

假设f(x)是我们求解的结果，F(x)是下边界值，G(x)是上边界值，则f(x)我们可以类似想到用夹逼准则的方式，看成是 F(x) <=f(x)<=G(x)，f(x)就是可信的。

从数学的角度，我们再来看一个问题，古代三大几何难题之一的化圆为方。如今计算圆的面积，我们直接套用公式即可轻易得到，可在过去，人们是却花费了大量的时间和精力。

圆面积公式的常规推导思路是:先把一个圆平均分成若干份，然后将其拼成近似的长方形，最后根据长方形与圆的关系推导出圆的面积公式。当时人们认为既然正方形的面积容易求，只需要想办法做出一个面积恰好等于圆面积的正方形。但是怎样才能做出这样的正方形又成为了另外一个难题。

这个起源于古希腊的几何作图题，在2000多年里，不知难倒了多少能人，直到19世纪，人们才证明了这个几何题，古代人的尺规作图法是解决不了该问题的。

关于圆面积，古代数学家的贡献如下：

我国古代的数学家祖冲之，从圆内接正六边形入手，让边数成倍增加，用圆内接正多边形的面积去逼近圆面积。古希腊的数学家，从圆内接正多边形和外切正多边形同时入手，不断增加它们的边数，从里外两个方面去逼近圆面积。

古印度的数学家，采用类似切西瓜的办法，把圆切成许多小瓣，再把这些小瓣对接成一个长方形，用长方形的面积去代替圆面积。16世纪天文学家开普勒，把圆分割成许多小扇形，圆面积等于无穷多个小扇形面积的和，各段小弧相加就是圆的周长2πR，最后得出我们今天计算圆面积的公式。

通过今天的计算可以得到：在一个圆里画一个最大的正方形，正方形占圆面积的约63.7%，在一个圆外画一个最小的正方形，正方形面积是圆形面积的157%。

看看，古人计算圆面积的思想和费米估计的思想是不是有异曲同工之妙呢？

四、案例分析

在互联网领域的工作面试中，如数据分析、产品、市场和咨询等岗位，费米问题经常被考到，题目往往能间接反映出候选人的综合素质。

下面，我们基于一个外卖业务，做一个分析。在北京地区，需要多少骑手才能满足用户的外卖需求呢？

（1）明确问题

对于一家外卖平台，如果能提前估算出平台所需要的骑手人数，首先对人力资源方面会节省非常大的成本，其次可以根据商业模式提前计算业务数据，比如定价、订单分发、补贴、骑手支出等。给业务提供许多决策依据。

（2）问题拆解

北京地区每天有多少单外卖需求？1个骑手1天能够完成多少单任务？1个骑手完成一单的花费时间是多少？

每单花费时间：前往商家时间+排队等待时间+从商家到目标地点时间+等待用户时间。

（3）明确常识性数据

根据2019年公布的数据，北京人口总数2153.6万人，网民渗透率90%以上，对于外卖的目标用户主要锁定在20-30岁易接受新鲜事物和消费能力强的年轻人，这部分人在人群中占比45%。

目标人群规模：2153.6*90%45=872.2万人。

需求频度：每人平均5天1次。

骑手每天工作有效时间：10h，吃饭休息除外。

商家距离：正常是3公里以内，我们取3公里为基数。

骑手速度：根据政策来说，电动车限速在25km/h。

排队等待时间为：10-20分钟，我们取15份，即0.25h。

商家到目的地距离：正常应该是3公里以内，3-5公里比较普遍，我们取4公里为基数。

用户等待时间：由于限时配送，我们认为都是按时或提起配送，基本无超时订单，所以用户等待时间为0h。

（4）设计计算公式

所需的骑手总数 = 每天订单总数/每人每天可配送的订单数

则可以确定以下数据：

每天的总订单数 = 目标用户数/点单频度 = 872.2/5 = 174.44万单

每人每天可配送的订单数 = 每天工作时间/完成一个订单需要的时间

= 每天工作时间/（骑手到商家的时间+排队等待时间+配送时间 + 用户等待时间）

= 每天工作时间/（商家距离/骑手速度+排队等待时间+目的地距离/骑手速度 + 用户等待时间 ）

= 10/（3/25 + 0.25 + 4/25 + 0）

= 18.9单

所需的骑手总数 = 每天订单总数/每人每天可配送的订单数 = 92296人

所以，最终得出的结论，北京应该有大约9万外卖骑手。

从上面的分析，我们也看到一个现实，每个骑手每天工作10小时，平均可以配送19单，新手的话可能更少，所以非常辛苦，这也能够激发大家的同理心，所以平时点外卖对于超时的订单要包容下。

除了上面的问题，类似这样奇怪的问题还有：

一个正常成年人有多少根头发？

在没有其他公开资料，你所在城市有多少个加油站？

地铁口的煎饼摊子一年能卖出多少个煎饼？

一辆公交车里能装下多少个乒乓球？

一个人一生会长出多长的手指甲？

估算你所在城市有多少家奶茶店？

除了上面的问题，类似这样奇怪的问题还有：

一个正常成年人有多少根头发？

在没有其他公开资料，你所在城市有多少个加油站？

地铁口的煎饼摊子一年能卖出多少个煎饼？

一辆公交车里能装下多少个乒乓球？

一个人一生会长出多长的手指甲？

估算你所在城市有多少家奶茶店？

总结：费米问题是现实世界最好的估算法，能够把限定信息、复杂困难的问题通过分解成常识性、可解决的小问题处理，所谓大事化小小事化了，这种思维方式非常实用，通过本篇，希望可以帮助你解决更多问题。

最后

以上就是唠叨高跟鞋为你收集整理的逻辑推理篇：数据分析最爱用的估算法：费米估计的全部内容，希望文章能够帮你解决逻辑推理篇：数据分析最爱用的估算法：费米估计所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。