1、概念
相关思维是数据分析中最常见的思维之一,在我们观察指标变化的时候,往往需要观察指标之间的相关关系,比如观察自己身高和体重的变化,这就是一种相关思维的体现。
衡量指标之间的相关关系,常见的相关性分析方法如下:
图表分析
皮尔逊相关系数
协方差
卡方检验
-
图表分析
- 对于一般的属性关系,我们采用简单的绘图方式就能够看出二者的属性关系,常见的图形有散点图/折线图。
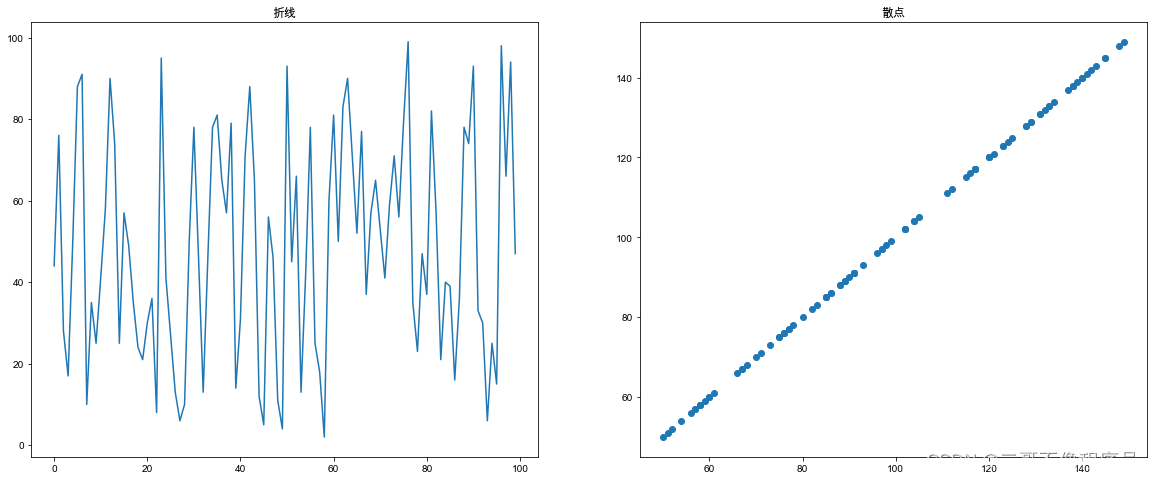
-
皮尔逊相关系数
- P ( X , Y ) = E ( X Y ) − E ( X ) E ( Y ) E ( X 2 ) − E 2 ( X ) E ( Y 2 ) − E 2 ( Y ) P(X,Y) = frac{E(XY)-E(X)E(Y)}{sqrt{E(X^2)-E^2(X)}sqrt{E(Y^2)-E^2(Y)}} P(X,Y)=E(X2)−E2(X)E(Y2)−E2(Y)E(XY)−E(X)E(Y)
- 皮尔逊相关系数通常用于衡量两个连续变量之间的相关程度,其取值是有界的,范围为[-1, 1],我们可以根据相关系数的取值(绝对值)来衡量两个变量的相关性:
- 0.8-1.0:极强相关
- 0.6-0.8:强相关
- 0.4-0.6:中等程度相关
- 0.2-0.4:弱相关
- 0.0-0.2:极弱相关或无相关
-
协方差
- c o v ( X , Y ) = E [ ( x − x ˉ ) ( y − y ˉ ) ] cov(X,Y)=E[(x-bar{x})(y-bar{y})] cov(X,Y)=E[(x−xˉ)(y−yˉ)]
- 协方差和皮尔逊一样通常用于两个连续变量之间相关性的检验,使用协方差判断相关性的结果比较直接,只有正相关、负相关、不相关三种结果。
- 当cov(X,Y)>0时,表明X和Y正相关
- 当cov(X,Y)<0时,表明X和Y负相关
- 当cov(X,Y)=0时,表明X和Y不相关
-
卡方检验
- 卡方检验可以用于离散和离散数据之间相关性的检验。(具体卡方检验的过程见后文的例子)
2、例:连续变量
连续变量之间的相关性
A公司2022年前6个月的广告投放金额为3.2, 4.2, 5.5, 5.0, 5.8, 8.5,每个月对应的利润为10.2, 11.1, 12.5, 12.8, 13.7, 15.0,我们如何确认广告投放和利润之间的相关性强弱呢,这时我们就可以使用上述的方法进行判断了。下面用Python计算相关系数举例:
import pandas as pd
data = pd.DataFrame({
"广告": [3.2, 4.2, 5.5, 5.0, 5.8, 8.5],
"利润": [10.2, 11.1, 12.5, 12.8, 13.7, 15.0]
})
data.corr()
结果如下:
| 广告 | 利润 | |
|---|---|---|
| 广告 | 1.000000 | 0.952401 |
| 利润 | 0.952401 | 1.000000 |
由结果可见,广告和利润之间的相关系数为0.952,由相关系数的判断标准来衡量,从数据上看他们二者是极强相关的。
3、例:离散变量
离散变量之间的相关性
现在需要检验某公司的不同广告和是否点击之间的关系,现有实际频数如下:
- 实际频数
| 点击 | 未点击 | 总计 | |
|---|---|---|---|
| 广告A | 3600 | 1400 | 5000 |
| 广告B | 2200 | 800 | 3000 |
| 总计 | 5800 | 2200 | 8000 |
由上述的条件可知,广告只有A和B两种,结果也只有点击与未点击两种,因此我们需要使用卡方检验的方式来进行相关性的判断。
- 假设
H0:广告和点击无关
H1:广告和点击相关
假设检验的基本思想是在假设成立的基础上去进行验证,因此我们可以计算出相应的期望频数如下:
| 点击 | 未点击 | 总计 | |
|---|---|---|---|
| 广告A | 3625 | 1375 | 5000 |
| 广告B | 2175 | 825 | 3000 |
| 总计 | 5800 | 2200 | 8000 |
- 期望的计算方式(以广告A的点击举例)
广告A的投放人数为5000,点击的总人数为5800,总体投放的总人数为8000,则广告A的点击期望频数为(5000*5800)/8000=3625。
- 卡方计算
- n:行数
- m:列数
- A:实际频数
- T:期望频数
χ 2 = ∑ i = 1 n ∑ j = 1 m A i j − T i j T i j chi^2=sum_{i=1}^{n}sum_{j=1}^{m}frac{A_{ij}-T_{ij}}{T_{ij}} χ2=∑i=1n∑j=1mTijAij−Tij
χ 2 = ( 3600 − 3625 ) 2 3625 + ( 1400 − 1375 ) 2 1375 + ( 2200 − 2175 ) 2 2175 + ( 800 − 825 ) 2 825 = 1.67 chi^2=frac{(3600-3625)^2}{3625}+frac{(1400-1375)^2}{1375}+frac{(2200-2175)^2}{2175}+frac{(800-825)^2}{825}=1.67 χ2=3625(3600−3625)2+1375(1400−1375)2+2175(2200−2175)2+825(800−825)2=1.67
- 结果对照
得到卡方计算的结果之后,我们需要进行查表来确定概率:

根据表格可以得到,我们计算的统计量的结果为1.67,介于1.323和2.072之间,因此我们可以说广告和点击有关成立的概率在0.75-0.85之间。
- Python计算
from scipy.stats import chi2_contingency
import pandas as pd
import numpy as np
df = pd.DataFrame({
'广告': ['A', 'A', 'B', 'B'],
'点击': [1, 0, 1, 0],
'频数': [3600, 1400, 2200, 800]
})
cross_tab = pd.pivot_table(data=df,
values='频数',
index='广告',
columns='点击',
margins=True,
aggfunc=np.sum)
print('卡方={0}nP值={1}'.format(*chi2_contingency(cross_tab)[:2]))
结果如下:
卡方=1.6718913270637408
P值=0.7958170415961258
- 结果解读
根据Python计算的结果,P值>0.05,因此我们得到的结论为广告和点击无关。
注意:卡方检验不能看到两个分类变量相关性的强弱,只能展示出他们是否相关。
最后
以上就是平常硬币最近收集整理的关于数据分析思维(二)|相关思维的全部内容,更多相关数据分析思维(二)|相关思维内容请搜索靠谱客的其他文章。








发表评论 取消回复