算法/动态规划/LongestCommonSubsquence(LCS)最长公共子序列问题

75 阅读 0 评论 50 点赞

我是靠谱客的博主单纯月亮，最近开发中收集的这篇文章主要介绍算法/动态规划/LongestCommonSubsquence(LCS)最长公共子序列问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

问题描述

一个字符串S，去掉零个或者多个元素所剩下的子串称为S的子序列。最长公共子序列就是寻找两个给定序列的子序列，该子序列在两个序列中以相同的顺序出现，但是不必要是连续的。

例如序列X=ABCBDAB，Y=BDCABA。序列BCA是X和Y的一个公共子序列，但是不是X和Y的最长公共子序列，子序列BCBA是X和Y的一个LCS，序列BDAB也是。

参考最长公共子串问题

思路一/暴力求解

对于每个X的子序列，检查是否为Y的子序列，并求出最长的一个。显然这个办法可行，但是所用的时间是指数级的：若X由n个字符构成，它的子序列有2^n个，Y由m个字符构成，子序列有2^m个，最终的时间复杂度为O(2^n * 2^m)

思路二/动态规划

为了节约重复求相同子问题的时间，引入一个数组，不管它们是否对最终解有用，把所有子问题的解存于该数组中，这就是动态规划法所采用的基本方法。

获得LCS长度
引入一个二维数组table[][]，用来存储临时LCS的长度。
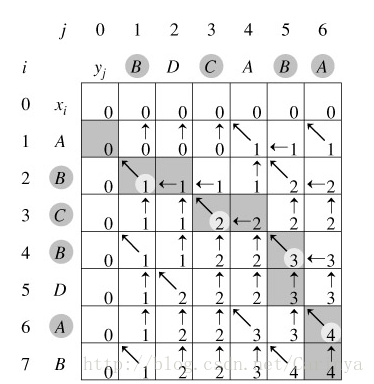
结合下图来看，当X[i]=Y[j]时，table[i][j]=table[i-1][j-1]+1，即左上角的值+1；
当X[i]!=Y[j]时，table[i][j]=max(table[i][j-1]，table[i][j-1])，即左和上的值取大。
遍历所有的i和j，建完表格以后，右下角的值table[X.length][Y.length]就是LCS的长度啦^

图片描述？

java代码如下：可以看到，getLCSLength是一个填表的过程

    private int getLCSLength(int m, int n) {
        table = new int[m + 1][n + 1];

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (x.charAt(i - 1) == y.charAt(j - 1)) {
                    table[i][j] = table[i - 1][j - 1] + 1;
                } else {
                    table[i][j] = max(table[i][j - 1], table[i - 1][j]);
                }
            }
        }
        return table[m][n];
    }

打印LCS

这里用到了回溯法(感谢神逸大神的博客^)。
因为LCS不一定只有一个，因此需要一个容器来存储它们，这里选择了TreeSet。
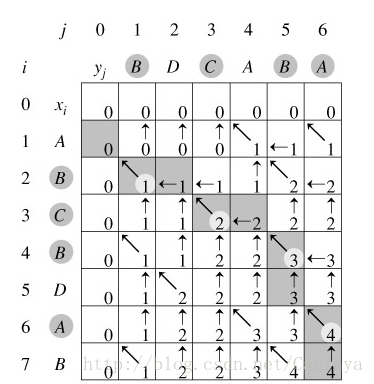
当X[i]=Y[j]时，将这个字符加入到子序列中，table[i][j]转入table[i-1][j-1]继续判断；
当X[i]!=Y[j]时，table[i][j]转入max(table[i][j-1]，table[i][j-1])，如果此时table[i][j-1]=table[i][j-1]，就说明不止一个LCS，这时候要用递归分别回溯两部分子序列，将找到的LCS填入set中，最后输出。

这里写图片描述

java代码如下：

    private void traceBack(String lcs_str, int i, int j) {
        while (i > 0 && j > 0) {
            if (x.charAt(i - 1) == y.charAt(j - 1)) {
                lcs_str += x.charAt(i - 1);
                i--;
                j--;
            } else {
                if (table[i - 1][j] > table[i][j - 1]) {
                    i--;
                } else if (table[i - 1][j] < table[i][j - 1]) {
                    j--;
                } else {
                    traceBack(lcs_str, i - 1, j);
                    traceBack(lcs_str, i, j - 1);
                    return;
                }
            }
        }
        set.add(reverse(lcs_str));
    }

    private void printLCSTrace() {
        int m = x.length();
        int n = y.length();
        int length = getLCSLength(m, n);
        String str = "";
        traceBack(str, m, n);

        System.out.println("The length of LCS is " + length);
        set.forEach(System.out::println);
    }

完整代码：

import java.util.TreeSet;

public class LCS {
    private String x;
    private String y;
    private int[][] table;
    private TreeSet<String> set = new TreeSet<String>();


    private LCS(String x, String y) {
        this.x = x;
        this.y = y;
    }

    private int max(int a, int b) {
        return a > b ? a : b;
    }

    private int getLCSLength(int m, int n) {
        table = new int[m + 1][n + 1];

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (x.charAt(i - 1) == y.charAt(j - 1)) {
                    table[i][j] = table[i - 1][j - 1] + 1;
                } else {
                    table[i][j] = max(table[i][j - 1], table[i - 1][j]);
                }
            }
        }
        return table[m][n];
    }

    private String reverse(String str) {
        return new StringBuffer(str).reverse().toString();
    }

    private void traceBack(String lcs_str, int i, int j) {
        while (i > 0 && j > 0) {
            if (x.charAt(i - 1) == y.charAt(j - 1)) {
                lcs_str += x.charAt(i - 1);
                i--;
                j--;
            } else {
                if (table[i - 1][j] > table[i][j - 1]) {
                    i--;
                } else if (table[i - 1][j] < table[i][j - 1]) {
                    j--;
                } else {
                    traceBack(lcs_str, i - 1, j);
                    traceBack(lcs_str, i, j - 1);
                    return;
                }
            }
        }
        set.add(reverse(lcs_str));
    }

    private void printLCSTrace() {
        int m = x.length();
        int n = y.length();
        int length = getLCSLength(m, n);
        String str = "";
        traceBack(str, m, n);

        System.out.println("The length of LCS is " + length);
        set.forEach(System.out::println);
    }

    public static void main(String[] args) {
        LCS lcs = new LCS("xzyzzyx", "zxyyzxz");
        lcs.printLCSTrace();
        LCS lcs2 = new LCS("ALLAAQANKESSSESFISRLLAIVAD", "KLQKKLAETEKRCTLLAAQANKENSNESFISRLLAIVAG");
        lcs2.printLCSTrace();
    }
}