1.绪论

a

a1.计算

day1
对象：规律、技巧
目标：高效、低耗
计算机是工具和手段，而计算才是目标
绳索计算机及其算法（勾股定理）
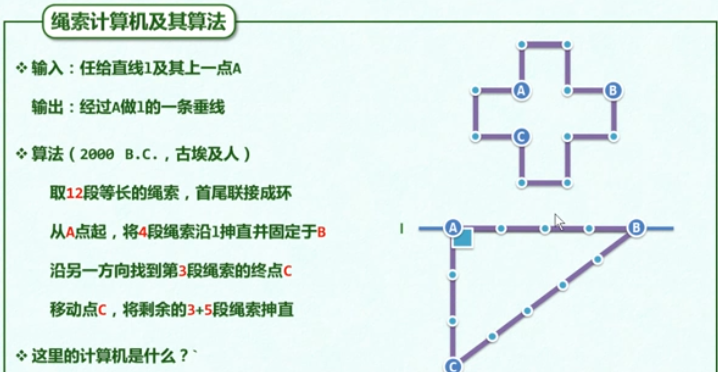尺规计算及其算法（相似三角形）

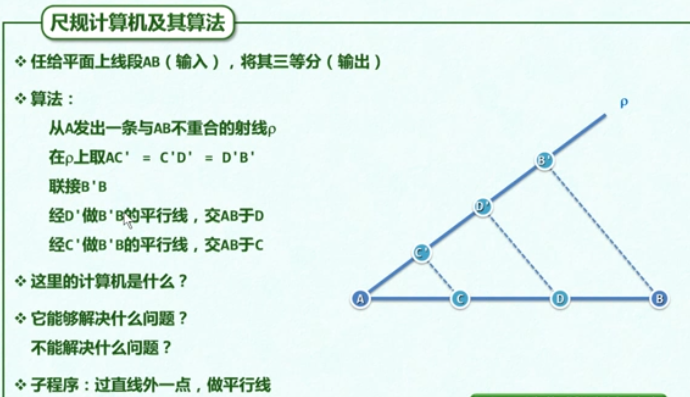
a2.算法

●计算 = 信息处理
借助某种工具，遵照一定规则，以明确而机械的形式进行
●算法，特定计算模型下，旨在解决特定问题的指令序列

●算法：有穷性
程序未必是算法：比如程序死循环
●好算法

b

b1. 计算模型

to measure is to know
●算法分析
两个主要方面：正确性（数学证明）和成本（时间和空间成本）
●成本

b2.图灵机

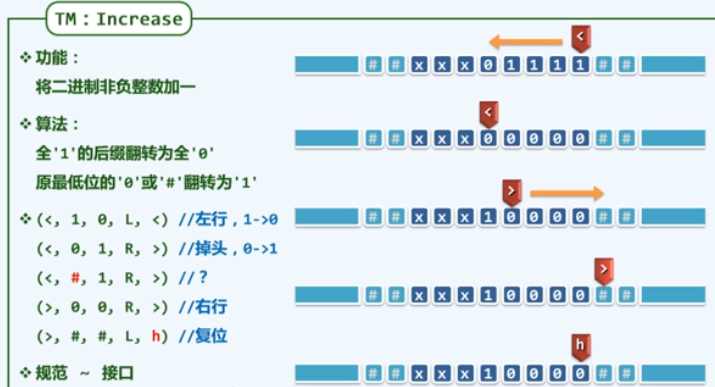
b3. RAM(random access machine)

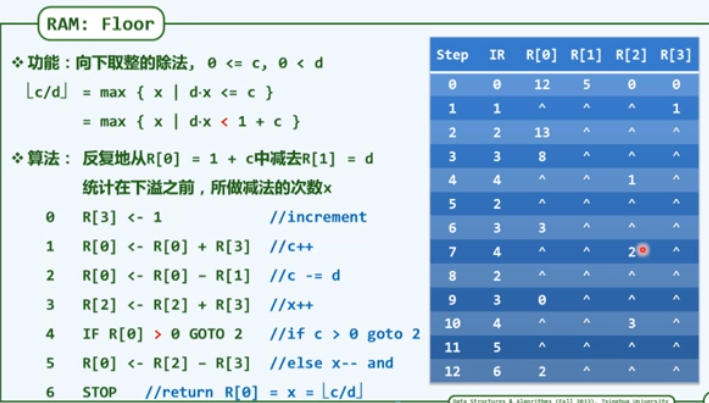
图灵机模型和RAM模型都是尺子

c

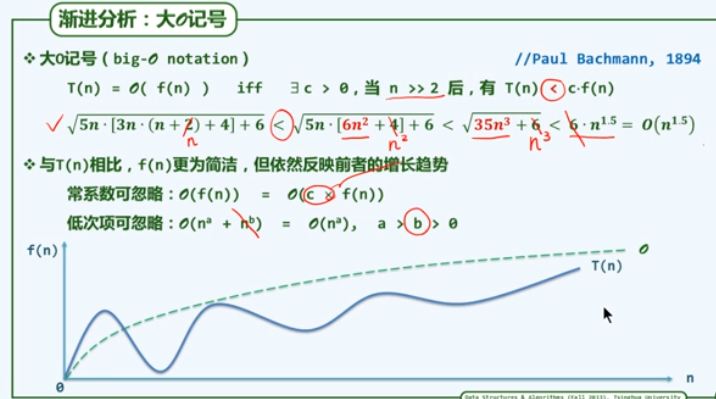
c1. 大O记号

渐进分析：在问题规模足够大后，计算成本如何增长（更关心足够大的问题）
需执行的基本操作次数：T(n)
需占用的存储单元数：S(n)

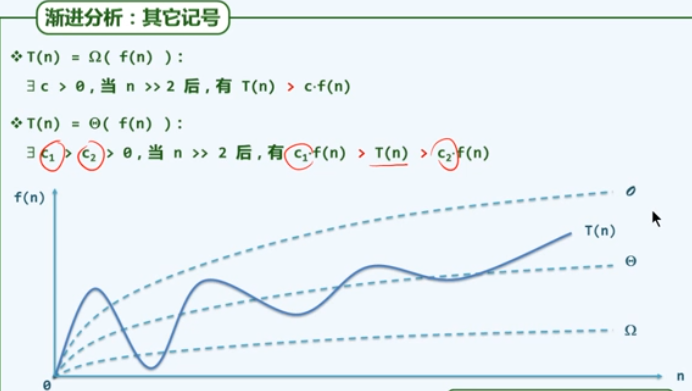
c2. big Ω，big Θ

c3.复杂度总结

day4

d

d1.算法分析

day9

d2.级数

将一个循环程序等效为不断的投硬币，直到第一次出现反面朝上。（正面朝上概率为 λ）需要投掷的次数可能是1次、2次、3次，…,符合几何分布，可以求解需要投掷次数的期望为1/（1 - λ）

d3.循环与级数

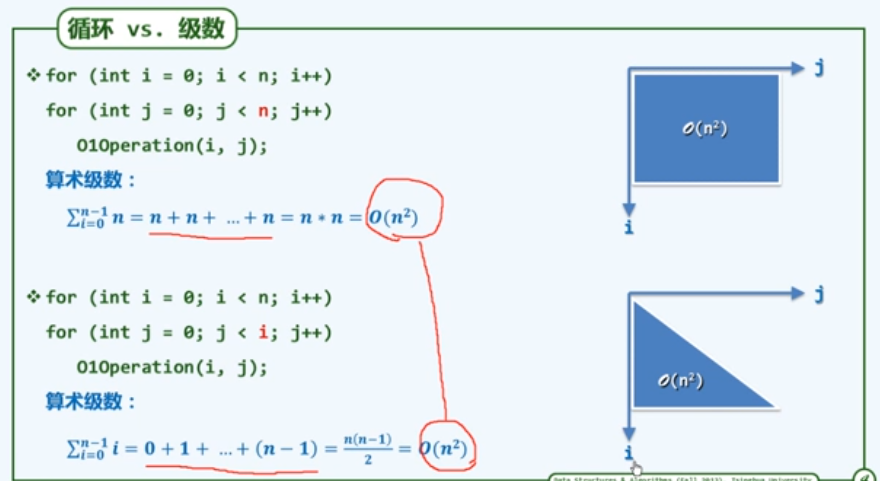
思考题
day10

d4 取非极端元素、冒泡排序

d5 起泡排序的分析

d6 封底估算

案例：估算地球的赤道的周长

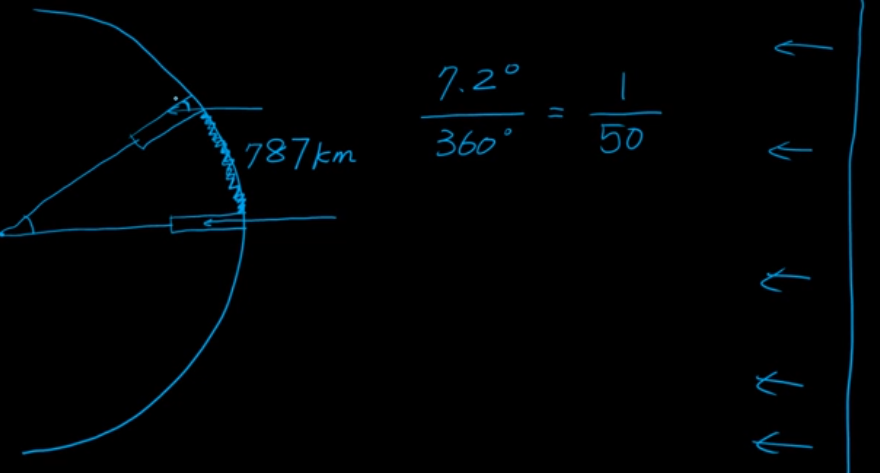
d7封底估算实例

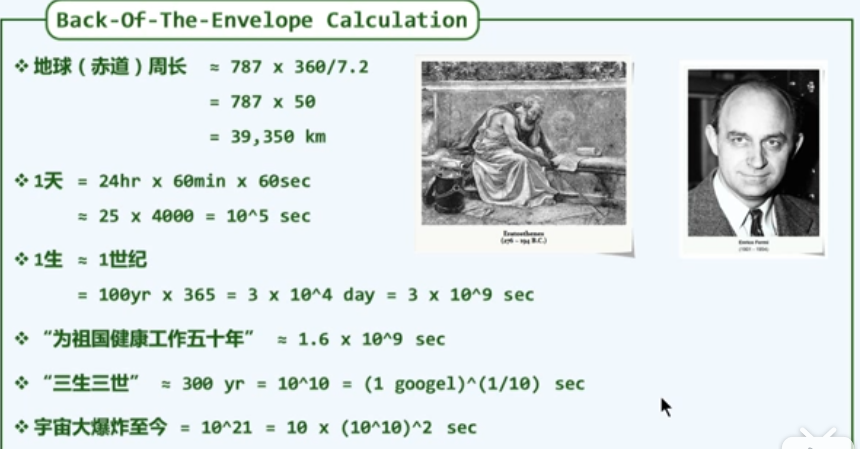在“三生三世”中的“1天”，相当于“1天”中的“1秒”
在“整个宇宙生命中”的“三生三世”，相当于在“三生三世”中的“0.1秒”（比例运算）

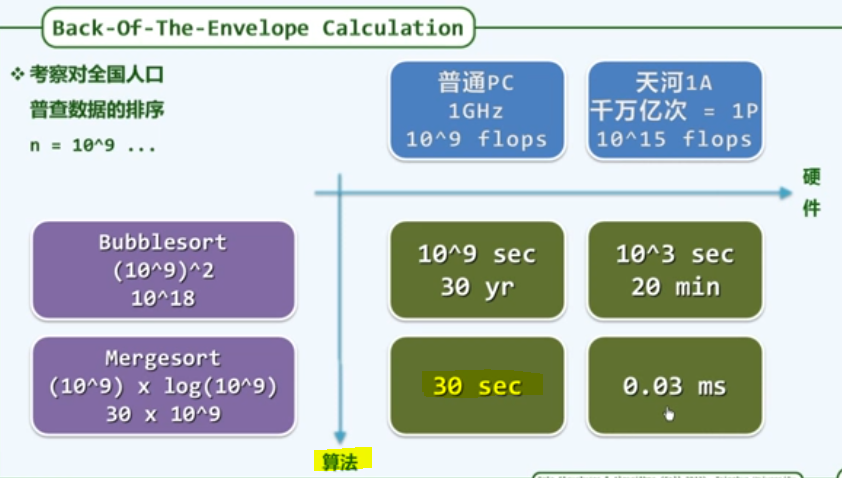
e 迭代与递归

e1 迭代和递归

e2 减而治之

e3 递归跟踪、递推方程

e4数组倒置

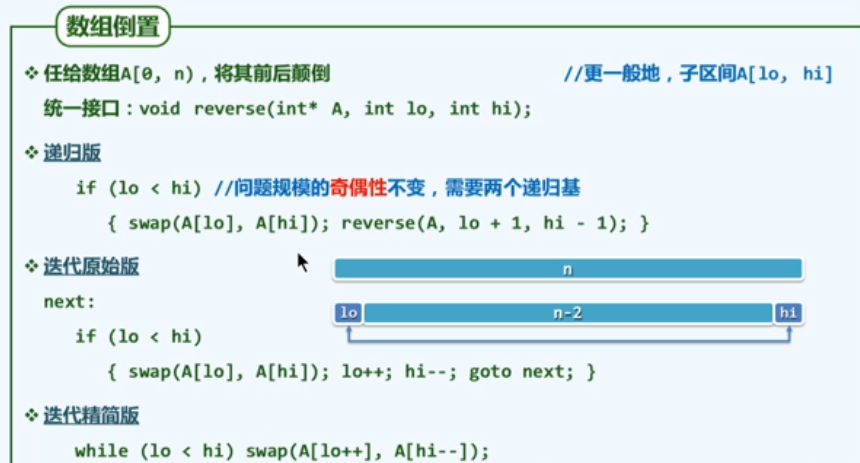
e5 分而治之

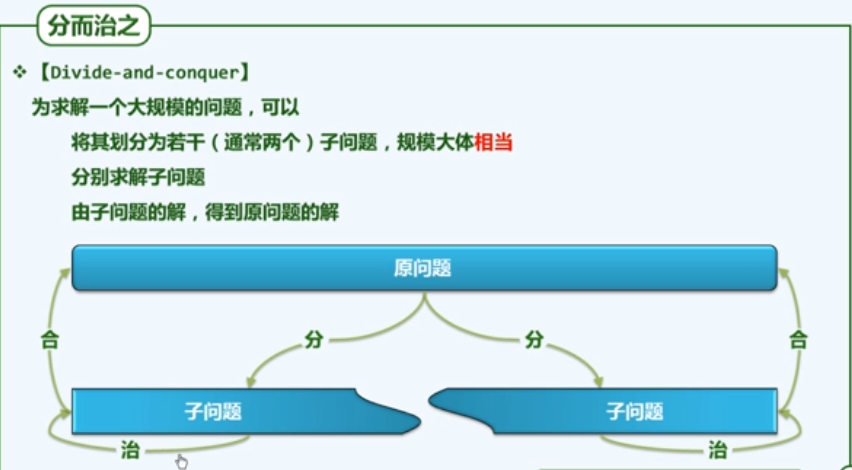
e6 例 数组求和–二分递归

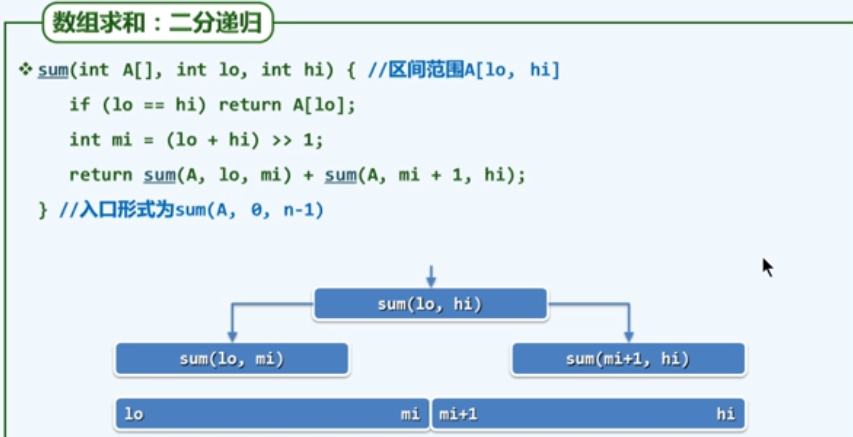上图复杂度分析：画图分析
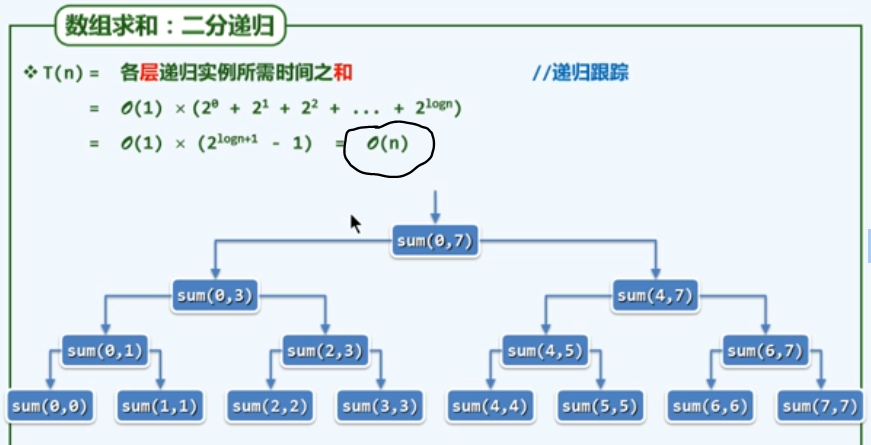上图O(n)的复杂度结果，可以直接套用前面几何级数的结果得出，从渐进的角度来说，最后一层的计算复杂度可以代表整体的复杂度。
上图复杂度分析：基于递归方程分析

e7 例 MAX2

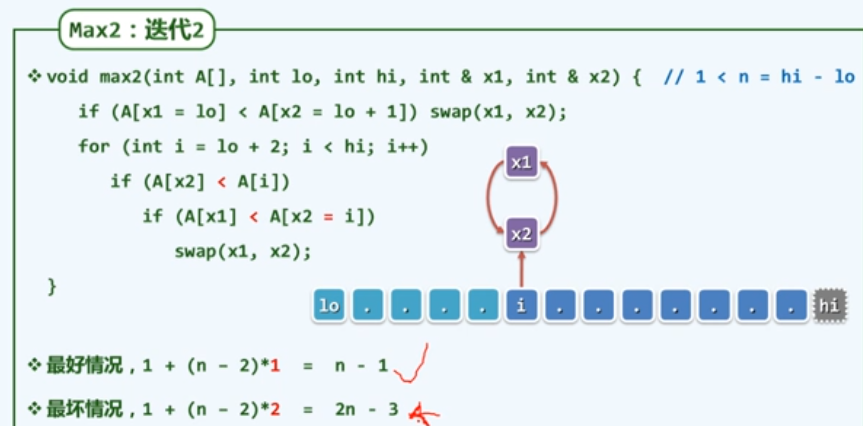
f 动态规划

f1 动态规划

由递归得到算法的本质，再将其转化为迭代

f2 fib递推方程

假设演绎法可以得出S(n) = fib(n+1)

f3 封底估算

10^9 flo:为一台普通计算机1秒可以做的运算次数。

f4 fib()递归跟踪

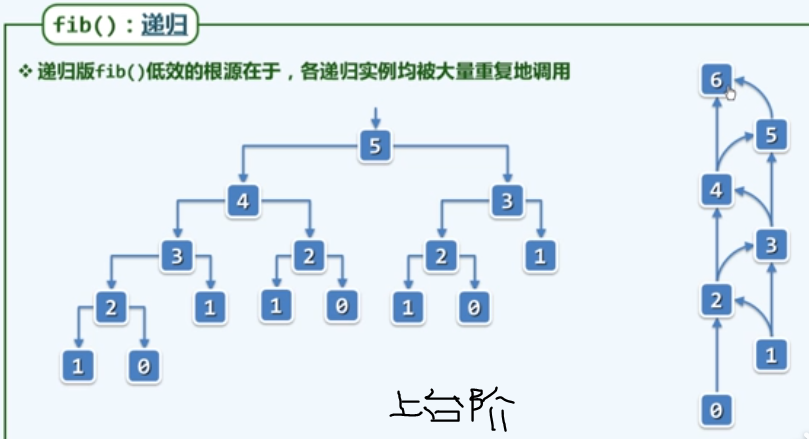上台阶问题：每次只能上一级或两级台阶，问到第n级台阶一共有多少种上去的方法，当n＞2时，fib(n) = fib(n-1) + fib(n-2);(最近一次是上一级台阶 or 最近一次是上两级台阶)，且f[1]=1,f[2]=2;

f5 fib()回归迭代

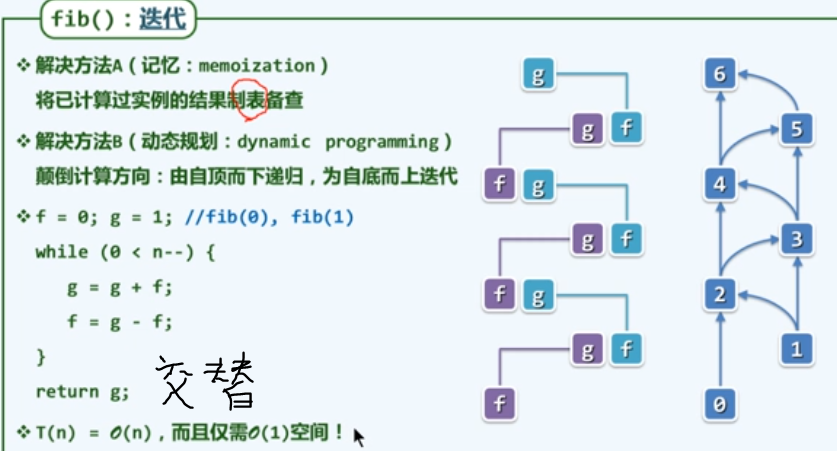
f6 最长公共子序列

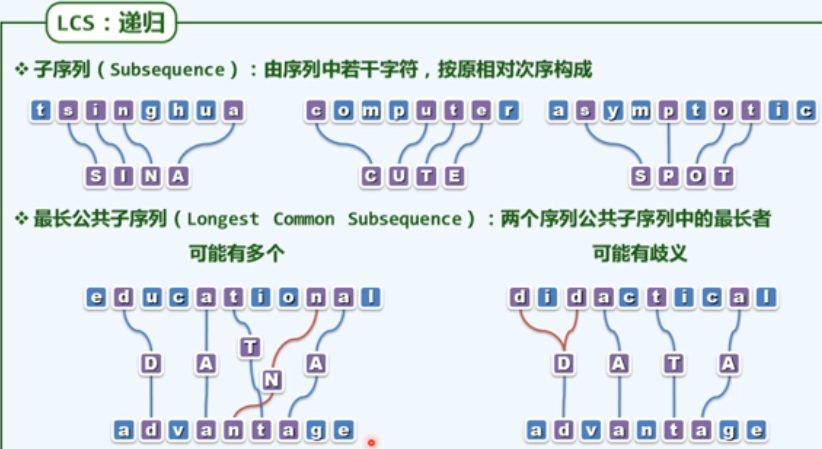
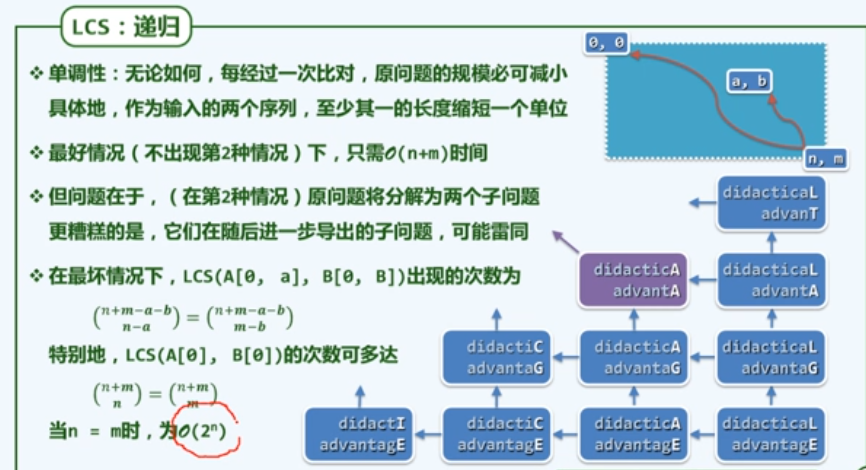
f7 递归LCS

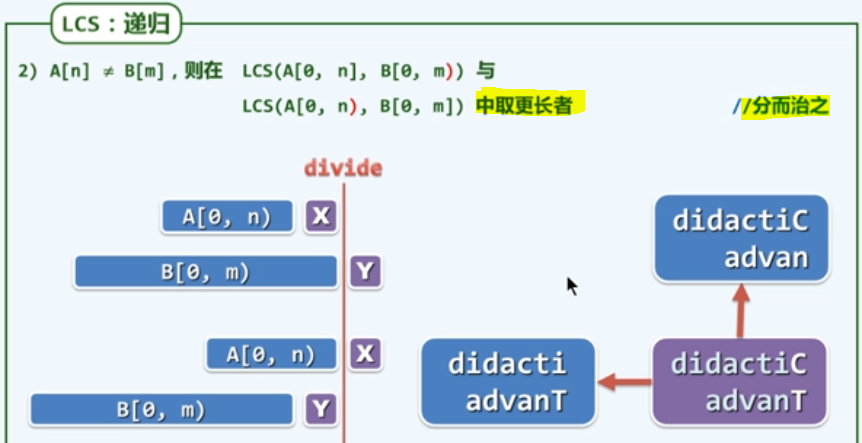代码实现上述思想

f8 理解LCS

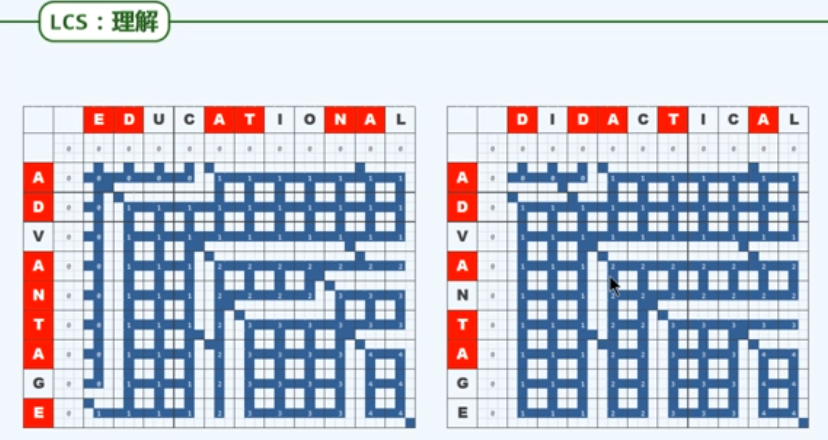
f9 动态规划LCS

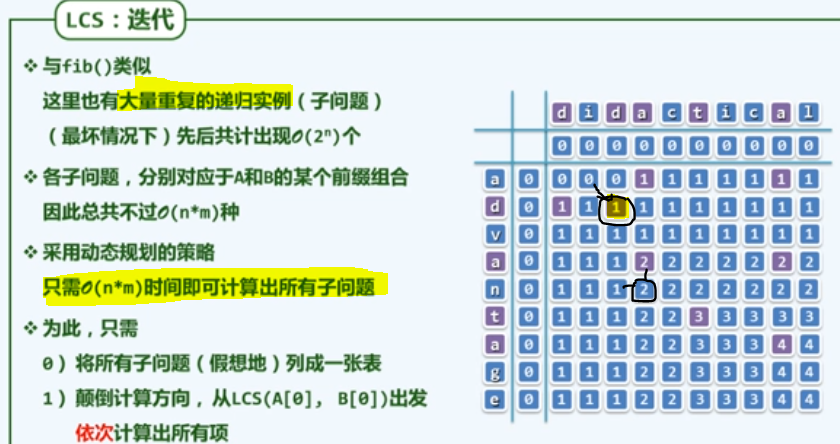参考：https://www.cnblogs.com/hapjin/p/5572483.html

最后

以上就是幽默钢笔最近收集整理的关于邓俊辉数据结构与算法学习笔记-第一章1.绪论的全部内容，更多相关邓俊辉数据结构与算法学习笔记-第一章1内容请搜索靠谱客的其他文章。