目录：

目录

C4.5分类树算法

C4.5的字段选择方法

C4.5的数值型字段处理方式、

C4.5的剪枝（避免过拟合）方法

---

主页：晴天qt01的博客_CSDN博客-数据分析师领域博主

目前进度：第四部分【机器学习算法】

C4.5分类树算法

上次我们说到ID3分类树【机器学习算法】决策树-2 ID3分类树算法的决策依据，ID3算法的4大缺点。_晴天qt01的博客-CSDN博客有4个缺点，C4.5就是为了解决这4个缺点而诞生的。

-C4.5的字段选择方法，C4.5的数值型字段处理方式、C4.5的剪枝（避免过拟合）作法

C4.5的字段选择方法

C4.5为了改善ID3的四个缺点，于是对分支依据进行了处理，从原本的information Gain转化为了 Gain Ratio=information Gain/information Value

Information Value,代表分支度，不过它并不是直接除以几条分支。它是看每条分支里有几笔数据，分支度就是用每个分支中的比例乘以以二为底的比例为对数的值。的累加求和（最后要加绝对值，或者负号）其实就是之前说的entropy

举个例子，如果其中一个分支只有一笔数据，那么它的information Value值就是-1/总数*log21/总数+其他值，这个值就会很大。那么information Value的值也会很大。

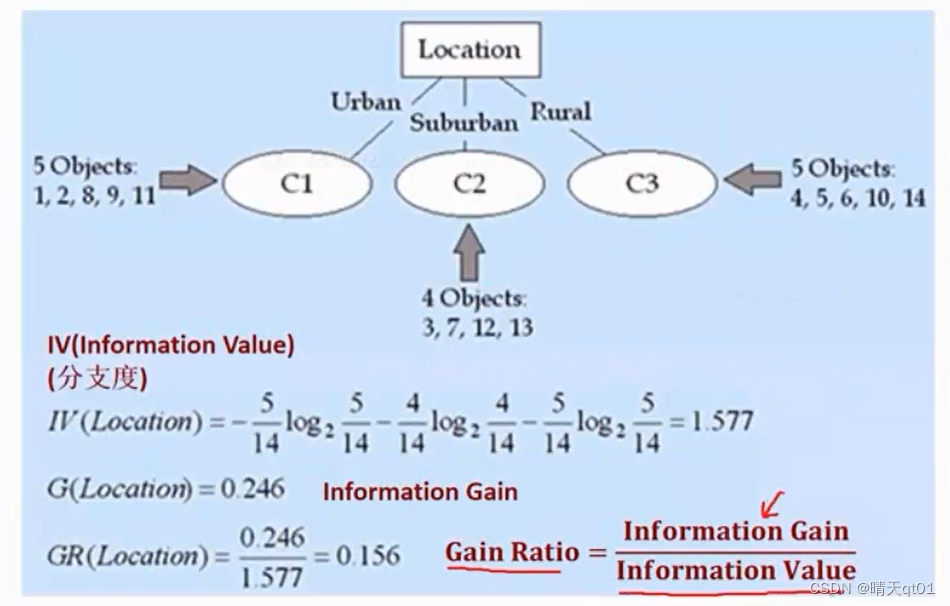
案例：

这里每列代表分支中的数量。每一行行都代表一种情况

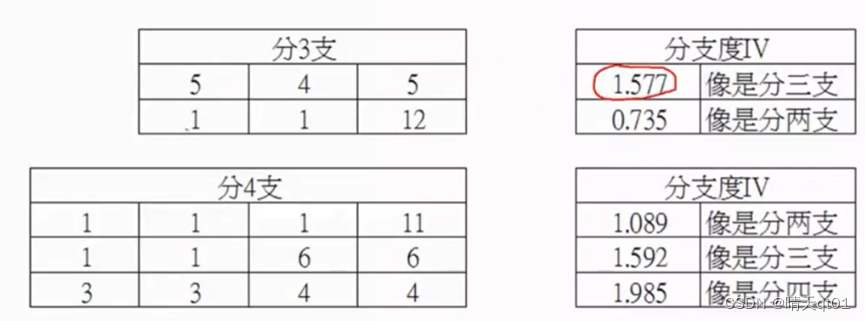
属于分支度不是单纯除以分支数，而是与笔数有关（本质是熵entropy）

结论，这里就解决了ID3分支过多的情况

C4.5的数值型字段处理方式、

另外C4.5会自动对数据进行离散化。它会将数值型字段，进行顺序排列，然后取其中一个数字点P1，进行切割。进行分箱，然后有n个值，那么就有n-1个节点可以切割。那么最后会判断gain ratio值的大小，来决定分几箱。

因为gain ratio会考虑分支个数。后来的CART也是用这种方法处理。

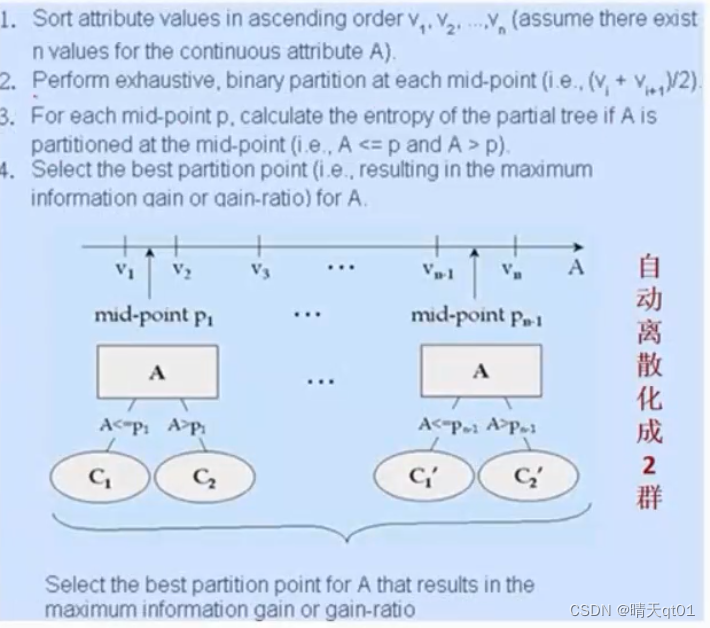
案例：

这里的年龄就是一个数值型字段，我们就对它进行切割，看那个地方切割比较合理。（通过判断获利比例gain ratio）

这里一共有10个数据，有有9个地方可以切割。算法就会都试一遍。这里如果我们在36.5的地方切割一下。

Entropy就打印0.69

Information Gain=0.28

Information Value=0.88（左边3笔数据右边7笔数据。）

Gain Ratio=0.28/0.88=0.32

如果这个是最优解了，那么我们就可以拿它gain ratio与其他字段的数值进行对比

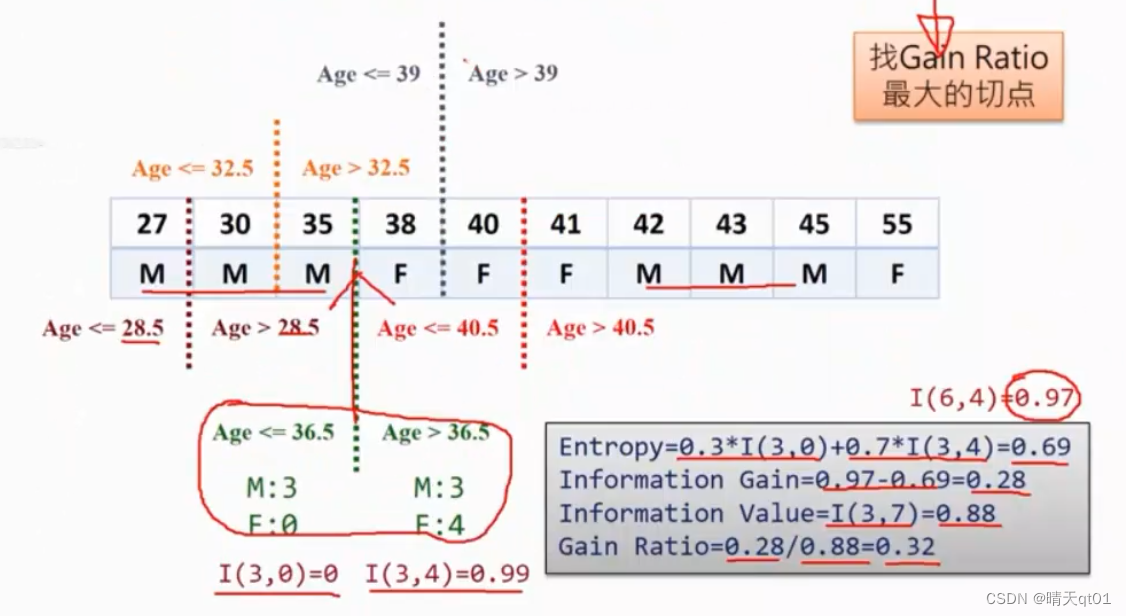
这里就解决了ID3只能对分类数据处理这个问题。

C4.5的剪枝（避免过拟合）方法

另外C4.5还会进行分类树剪枝方法，

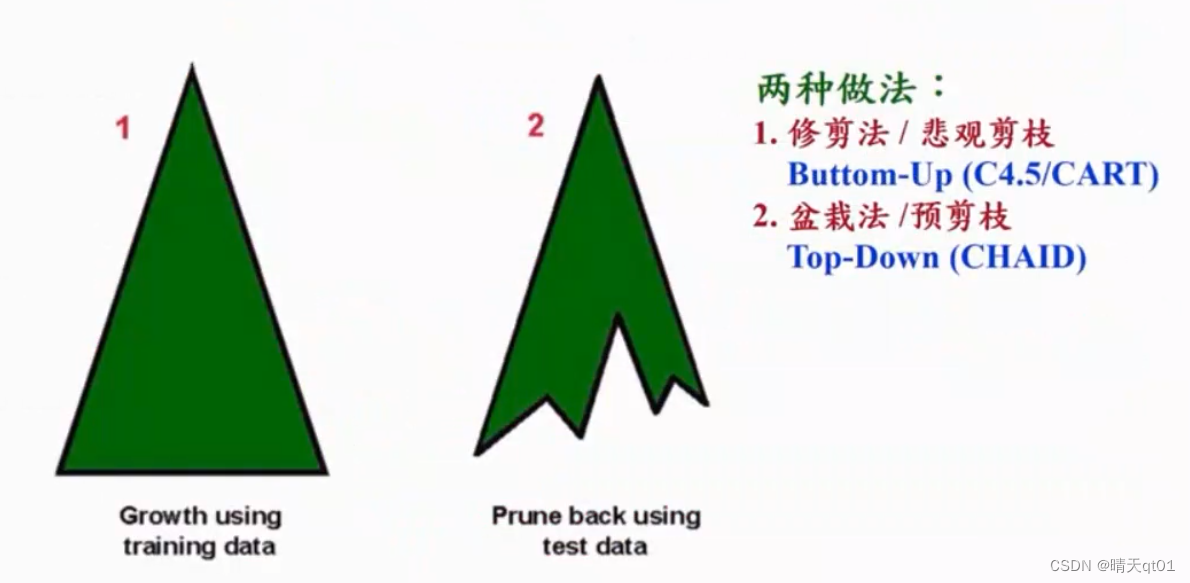
方法1：修剪法（悲观剪枝）：

方法一是先让分类树进行达到最优分类依据的结果，然后再对里面的分支进行修剪。是由下往上修改法。

CART和C4.5的修剪方法

方法2：盆栽法（预剪枝）

这个是在分类树进行生长的过程中，可能我发现诶，下一层会只有一笔数据，那么就不做生长了。就像是有一个模组，你只能生长到我规定的地方。

CHAID的修剪方法。

先说悲观剪枝，修剪法：

示意图

这里面有一个信心水平，最上方的那个数据。，就是如果决策树训练阶段分支里只有一笔数据，那么它正确的概率只有百分之25，这个是一个参数，是由我们调整的。如果这个数值越小，那么我们修剪的程度就越大。

就比如这个案例，里面B分类了3个分支，我们就对它进行一个统计参数的计算，代表它的错误率。因为训练数据正确，不代表测试数据也会正确。如果训练数据的数据量不够大，那么我们就认为它的正确率不高。

这里面我们用了U的公式，它会参考我们之前设置的参数，判断错误率。3个分支的错误率分别是，0.75,0.203,0.143，当数据量越来越多的时候，我们的错误率就会下降。

然后我们把这个错误率乘以每个分支内的笔数。（代表预期测试数据可能会出错的数目）进行求和。得到这一个字段分类，总共会出错多少数据。

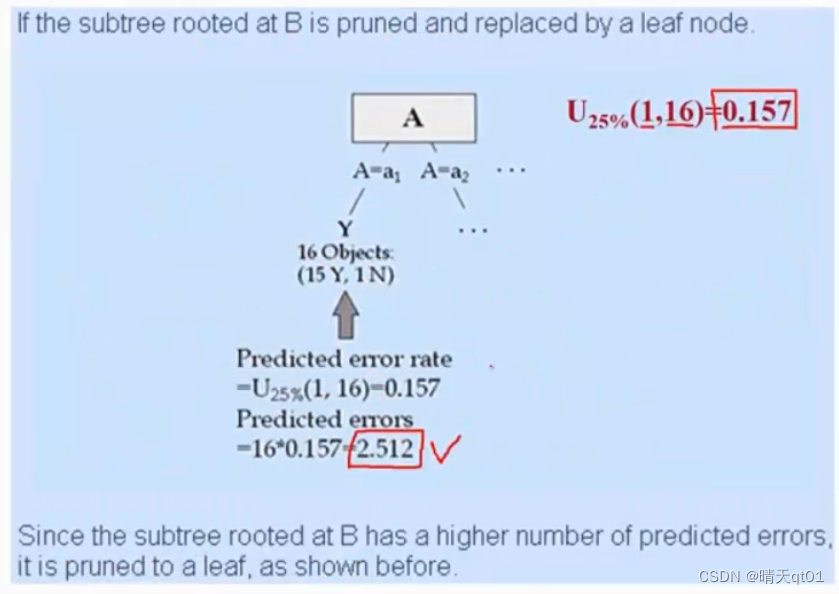
这个是树成长之后的错误数，那我们回过头，计算B的错误率，也就是不分支的错误数。用U分布来计算，得到0.157的错误率。乘以笔数，会出错2.512个数据。那么既然我们分支出错的数据量比不分支还大，我们就将这个树的分支砍掉。

然后砍掉这一个树之后，我们又会考虑，A作为字段依据是否需要砍掉。也是一样的方法。一直由下往上，直到不用砍树为止。

我们也可以运用到了e（错误率）来计算是否展开，原理是相同的，这个公式还蛮复杂的。这个e就是U

这个公式中N的节点资料笔数，E是有多少笔会分类错误。F就是E/N

Z的值是根据我们设定的错误率决定的，百分之25的条件下z就等于0.69

举例：

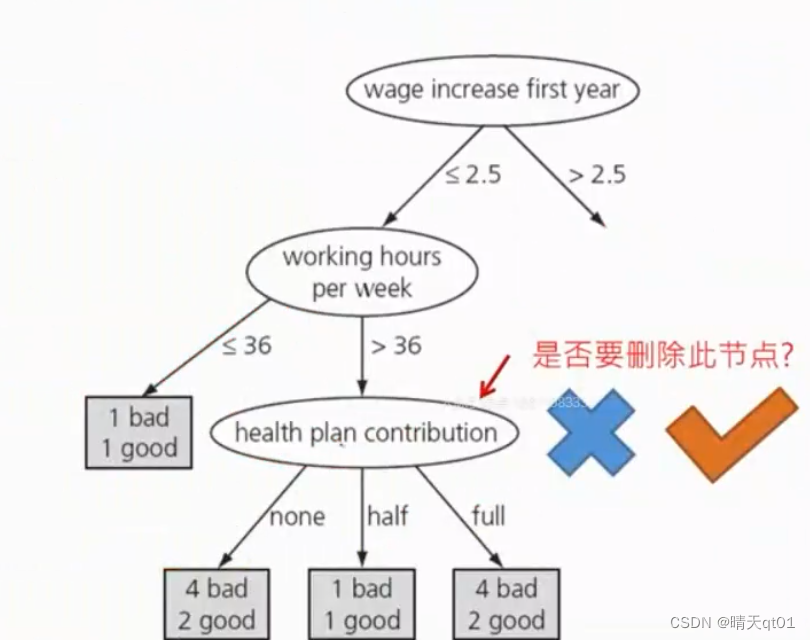
就拿左下角的案例来进行处理，这里面的N就是6，E就是少的那个，等于2，Z的值是0.69，然后我们带入公式，就可以求出它的这个节点错误率e=0.47

我们可以发现节点错误率是0.51

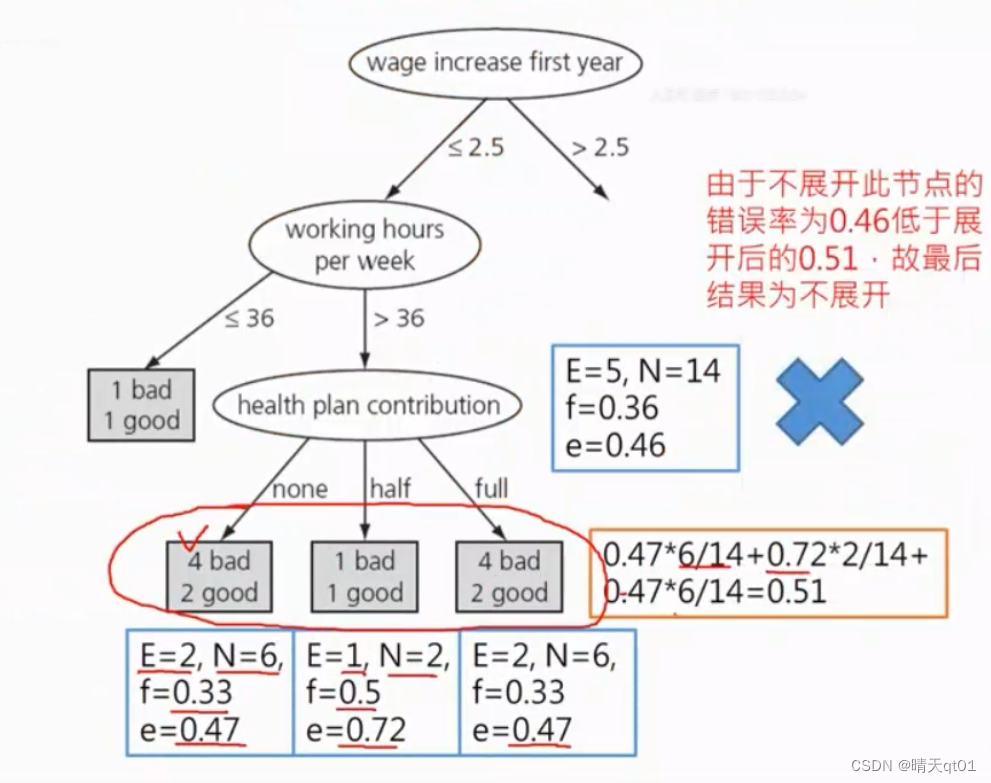
因为求出来整体的错误率还比单个的错误率还低，那我们就可以选择不展开。

C4.5也可以允许空值进入，这个还没讲。

决策树可以做：

预测申办信用卡的新客户是否将来会违约

银行针对特定群体做人寿保险的推销

根据生活作息推断病人得癌症的概率。

下次说CART算法，这个分类树可以同时做回归树和分类树。

最后

以上就是欢呼雪碧为你收集整理的【机器学习算法】决策树-3 C4.5的字段选择方法，C4.5的数值型字段处理方式、C4.5的剪枝（避免过拟合）方法C4.5分类树算法的全部内容，希望文章能够帮你解决【机器学习算法】决策树-3 C4.5的字段选择方法，C4.5的数值型字段处理方式、C4.5的剪枝（避免过拟合）方法C4.5分类树算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。