目录

前言

1 二阶系统LESO观测器设计

2.基于LESO的滑模控制器设计

​​​​3. 仿真分析(普通高增益项)

3.1仿真模型

3.2仿真结果

3.3 总结

4. 仿真分析(优化后的高增益项)

4.1 优化高增益项

4.2仿真结果

4.2.1 高增益①仿真结果

4.2.2 高增益②仿真结果

4.3 总结

5 学习问题

前言

上两篇文章我们介绍了扰动观测器和高增益观测器，顾名思义，扰动观测器就是观测未知的扰动，使我们系统针对扰动时能够“对症下药”；高增益观测器就是一种状态观测器，由于实际中系统并非都是理想的可直接测量的，所以需要借助观测器得到状态变量。

VSC/SMC（八）——基于慢时变干扰观测器的滑模控制(含程序模型)_Mr. 邹的博客-CSDN博客_慢时变干扰观测器

VSC/SMC（七）——基于高增益观测器的滑模控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客

本篇文章，继续介绍一种常见的扩张观测器，也就是我们文献中常看到的缩写：LESO，并且可以和控制器并行设计。

那为什么叫“扩张”？是因为它的结构上比系统多了状态变量。

好了我们开始介绍以及仿真分析吧。

1 二阶系统LESO观测器设计

先以一个简单的二阶系统为例进行设计，它的状态空间方程为如下标准形式：

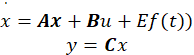
其中：

假设这个系统的状态变量是不可测的，为其设计如下的LESO：

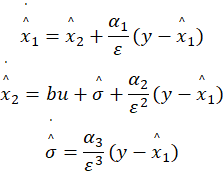
 其中，ε > 0，且α1、α2、α3均为正实数，即满足如下多项式为Hurwitz多项式：

观测器的状态变量为：

可以看到，比上述二阶系统的状态变量多了一个，实际上σ可以看成是对扰动f的一个观测/估计。

也有的文献直接将分式看成一个调节参数，如下:

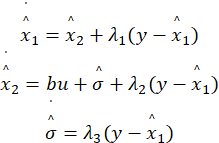
同理，λ1、λ2、λ3均为正实数。

还有的文献直接将误差变量进行观测，有兴趣的读者可以参考这篇：

《基于扩张观测器的非线性不确定系统输出跟踪---王新华》

对于稳定性分析，读者可以自行阅读文献，这里篇幅原因就不介绍了，谢谢理解！

2.基于LESO的滑模控制器设计

为了使x1能跟踪指令位置x1d，所以跟踪误差e = x1-x1d，并定义如下的线性滑模面：

 其中，c > 0。

注：其实这个滑模面是“中间”滑模面，“中间”指的是观测器，所以后面证明稳定性还是要引入第一级滑模面。

这里我还是应用等效滑模的思想设计控制律：

①对滑模面求导，有：

 ②选取等速趋近律，并且联立滑模导函数，有：

③Lyapunov稳定性证明

略...... 

所以得到得控制律为： 

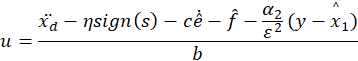
为了减少抖阵，取ηsign(s) = ηs ，进而得到：

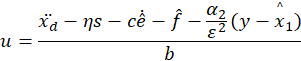
其中：

注：这里的误差是观测器与指令位置之间的误差，同理(x1^)'-(x1d)' = (e')^，即跟踪位置导数(速度)的观测误差。

​​​​3. 仿真分析(普通高增益项)

3.1仿真模型

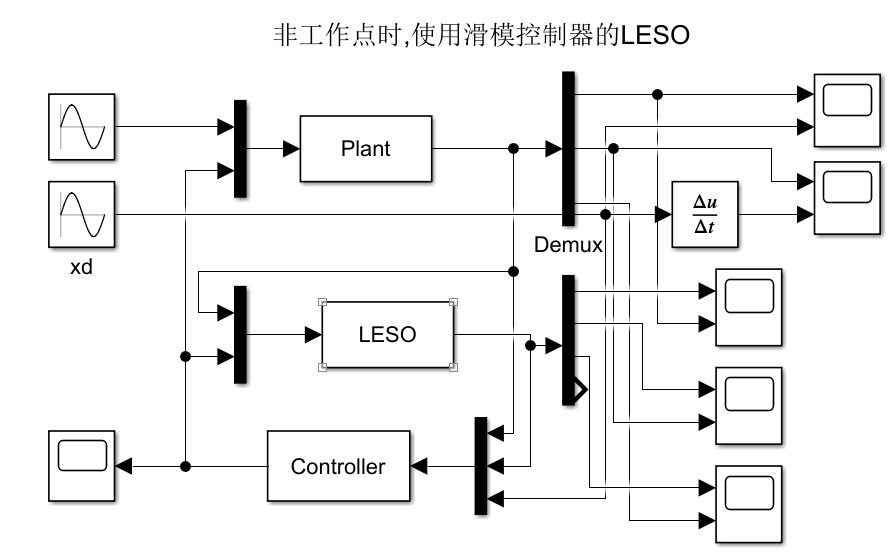
取上述系统b = 0.1，扰动d = 3*sin(t)，指令位置xd = sin(t)，并取初始状态为[0.5;0]，建立的simulink模型如下：

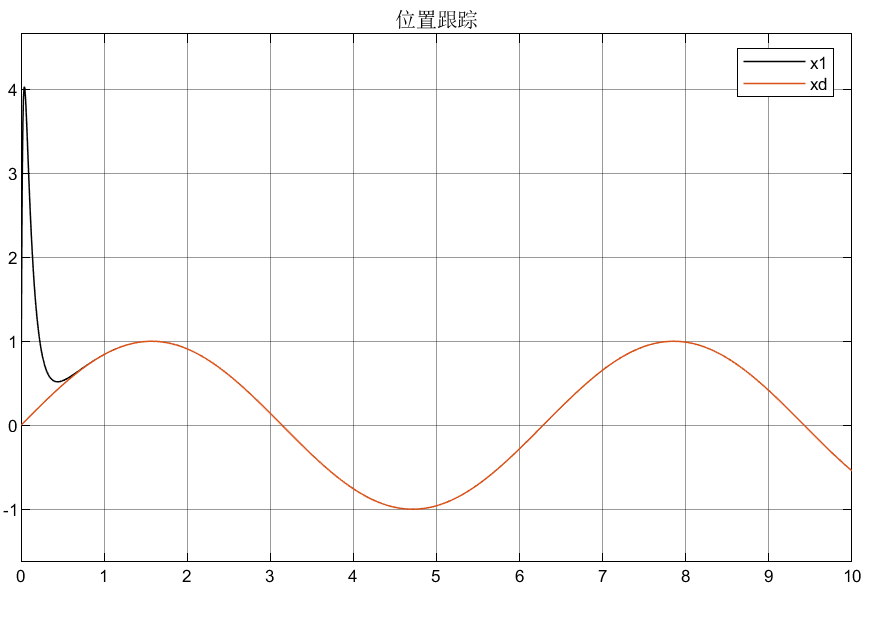
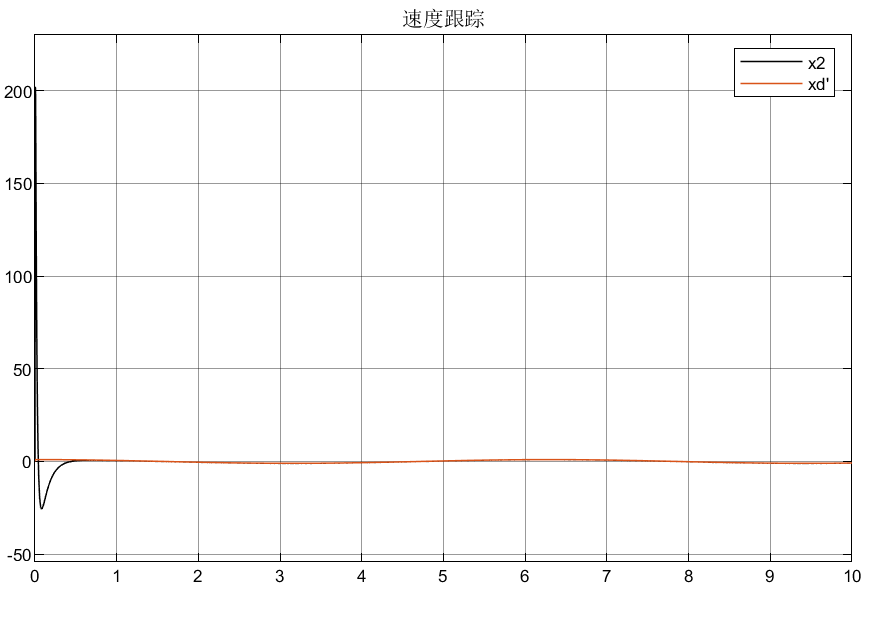
3.2仿真结果

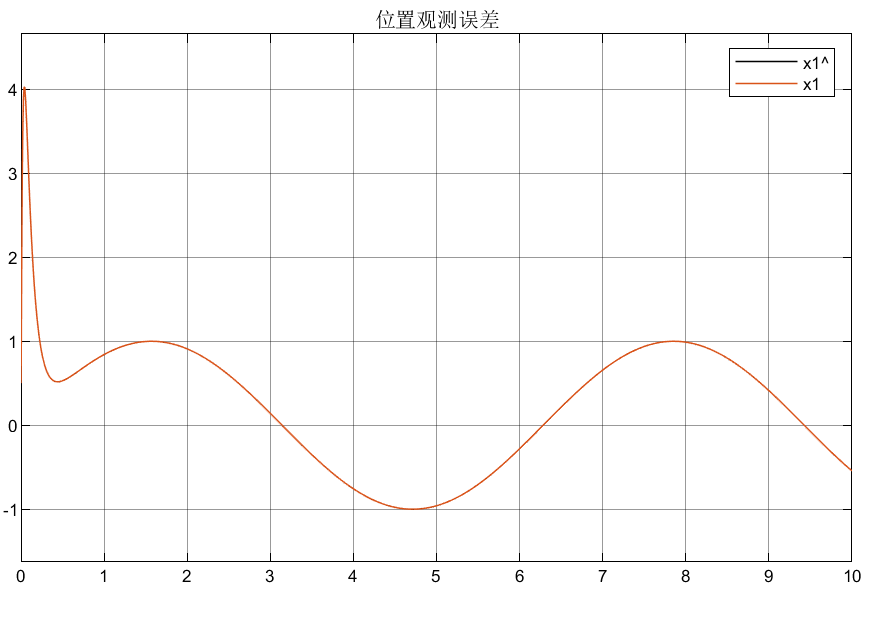
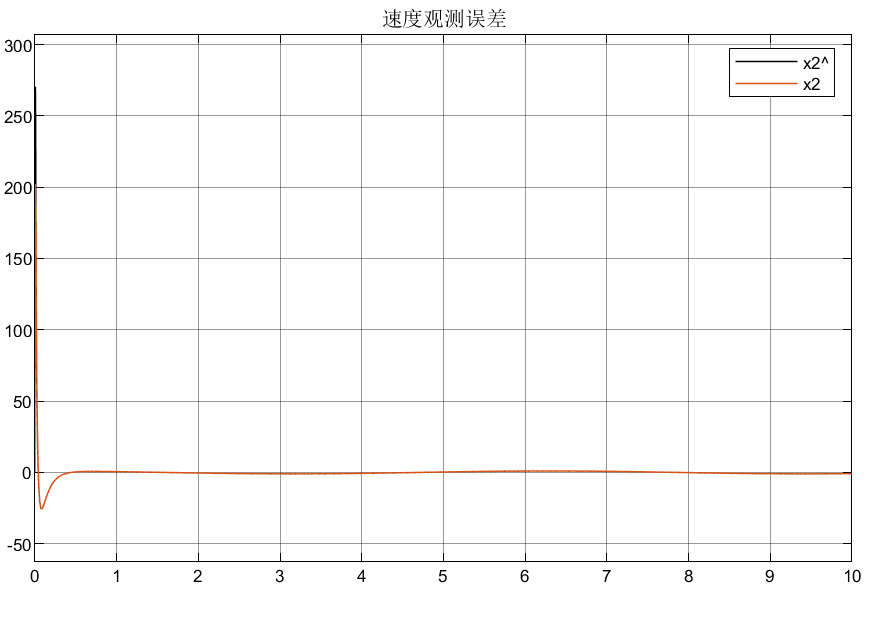
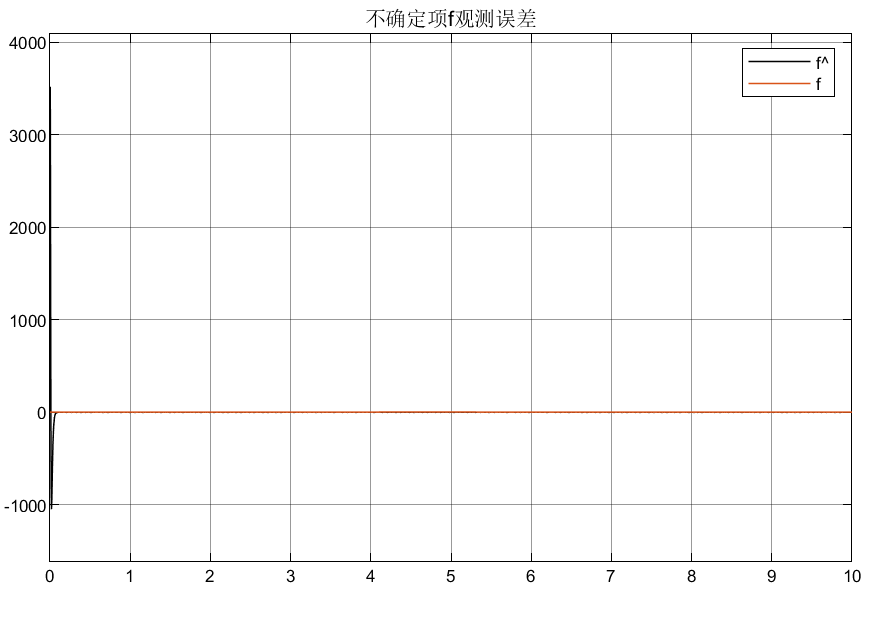
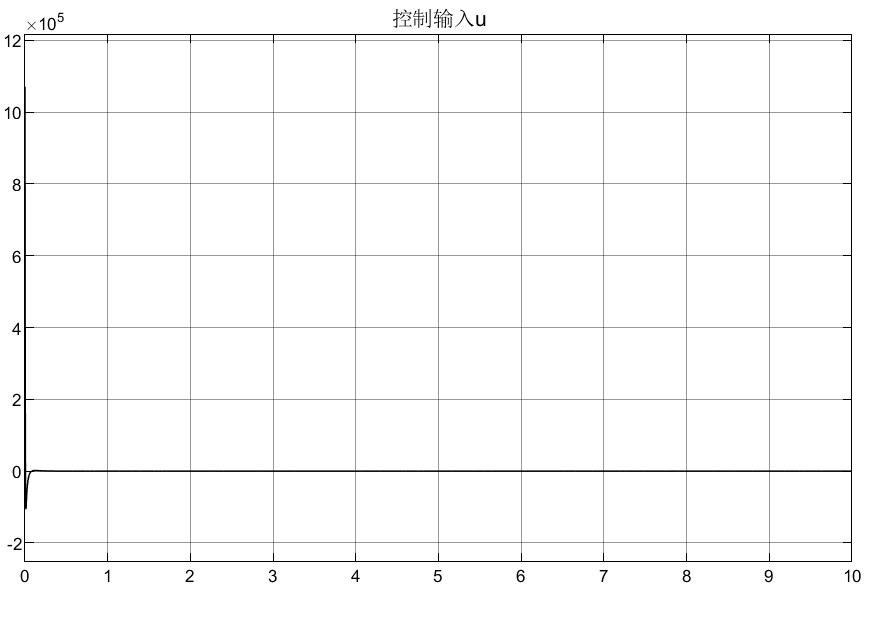
3.3 总结

优点：可以看到，这样的状态观测器因为有高增益的存在，所以能使跟踪误差迅速趋于0，即跟踪效果和反应速度很快；

缺点：但是导致了一个问题，由于高增益项的存在使得初始峰值很大，这样导致初始的误差很大，而且对控制器的伤害也很大，所以需要优化设计高增益项。

4. 仿真分析(优化后的高增益项)

4.1 优化高增益项

由于扩张观测器本质上也是一种高增益观测器，从上述的仿真结果我们可以看到虽然最终效果不错，但是如果扩张观测器的初始值与被控对象的初值不同，便会导致峰值现象，现在设计如下的两种高增益：

①

②

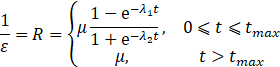
 其中，u > 0，λ1 > 0，λ2 > 0。

4.2仿真结果

4.2.1 高增益①仿真结果

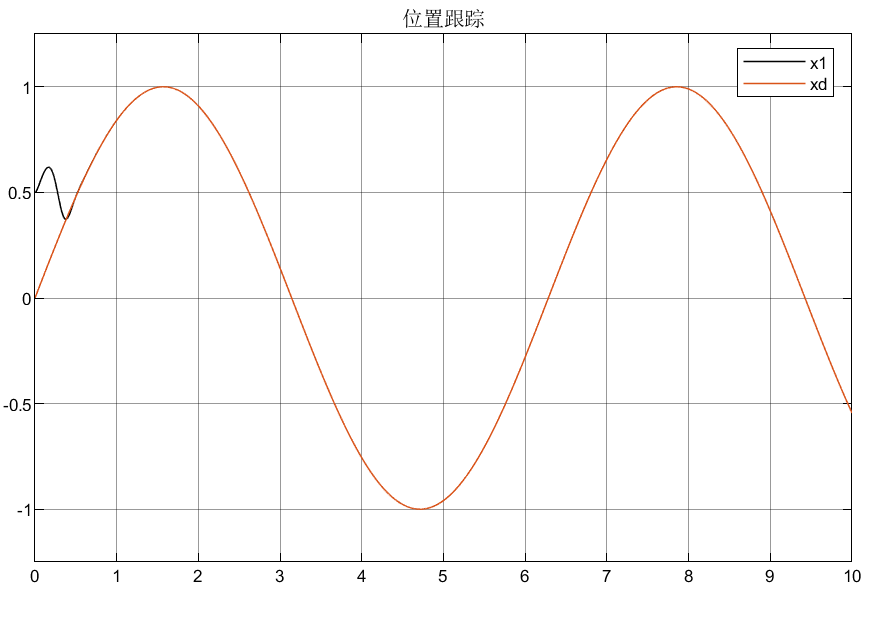
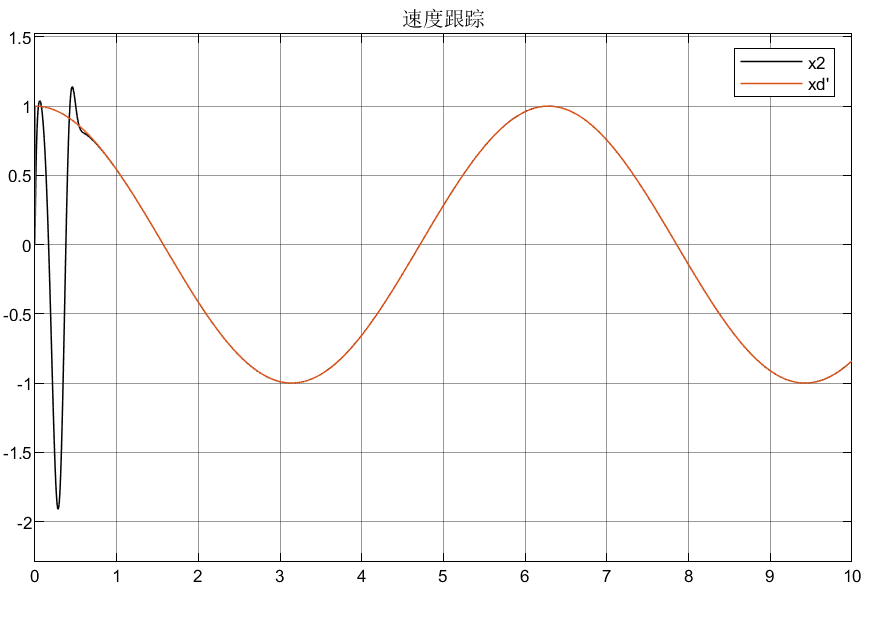
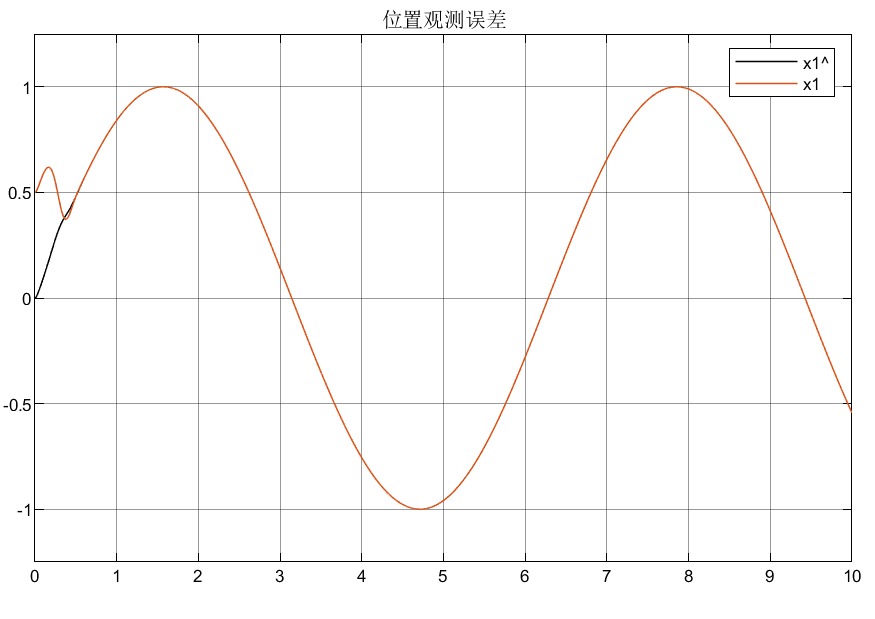
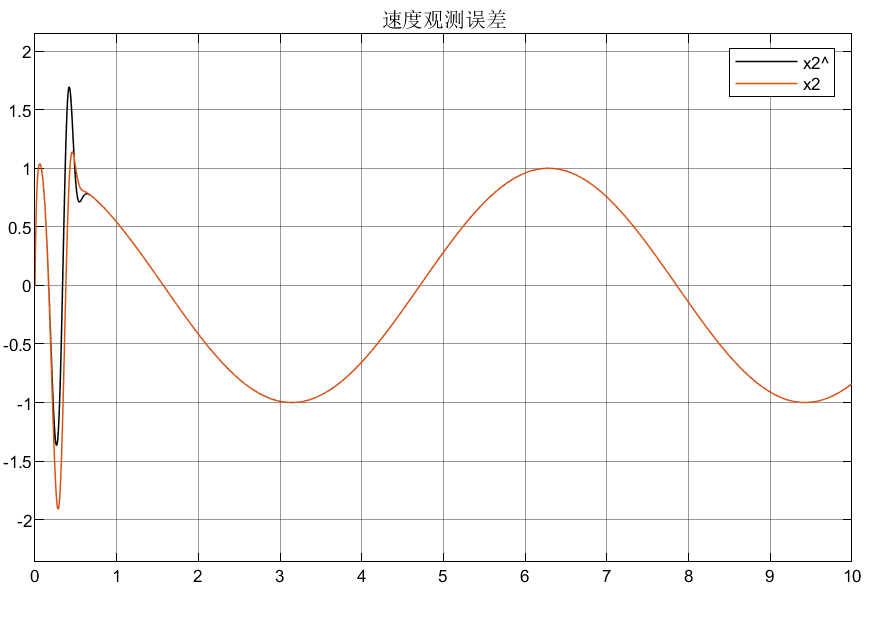
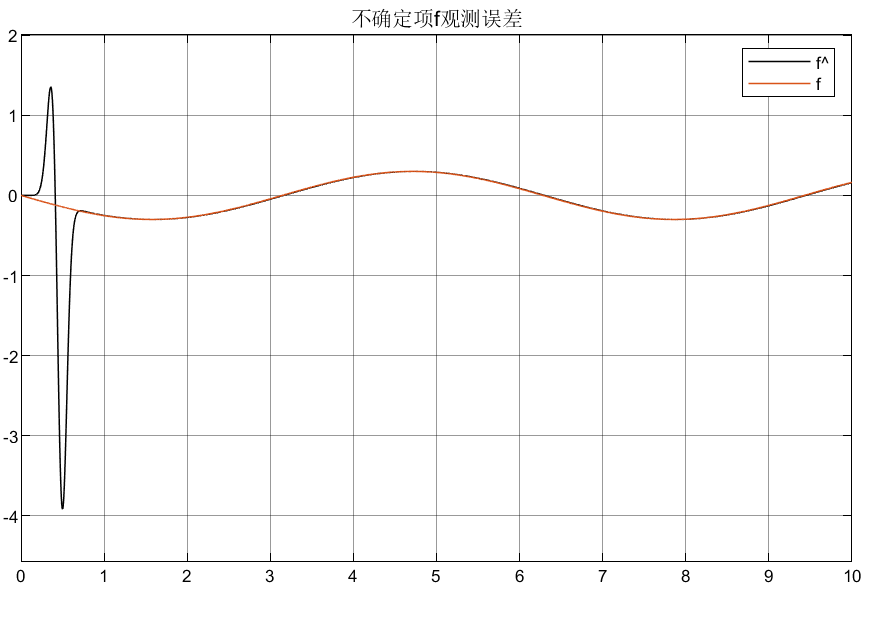
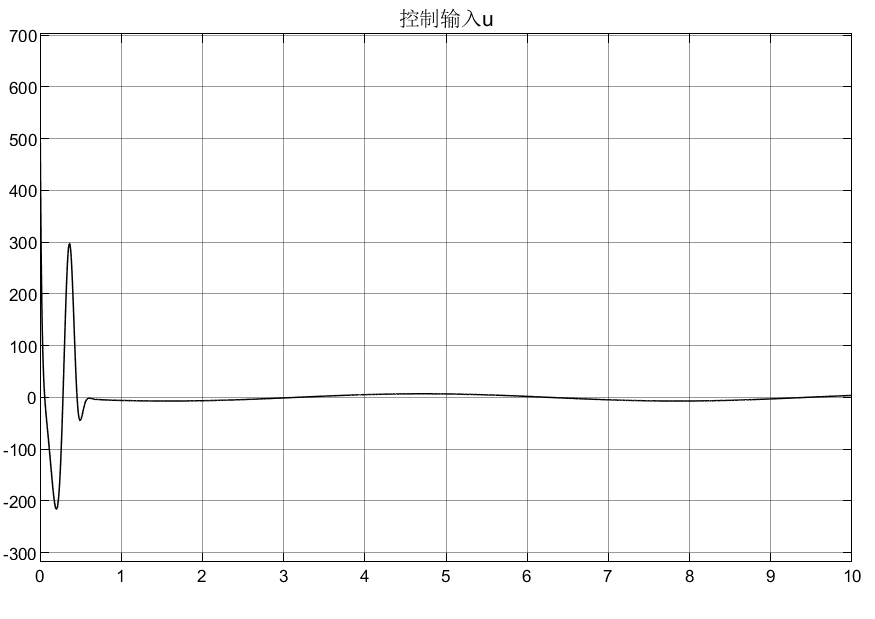
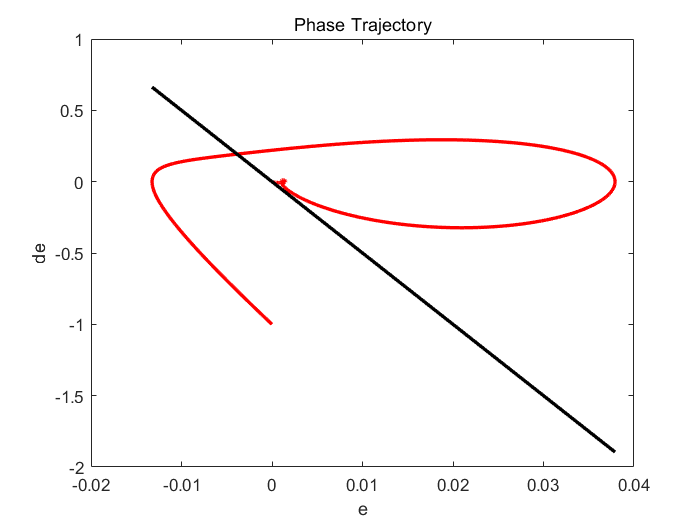
 ​​4.2.2 高增益②仿真结果

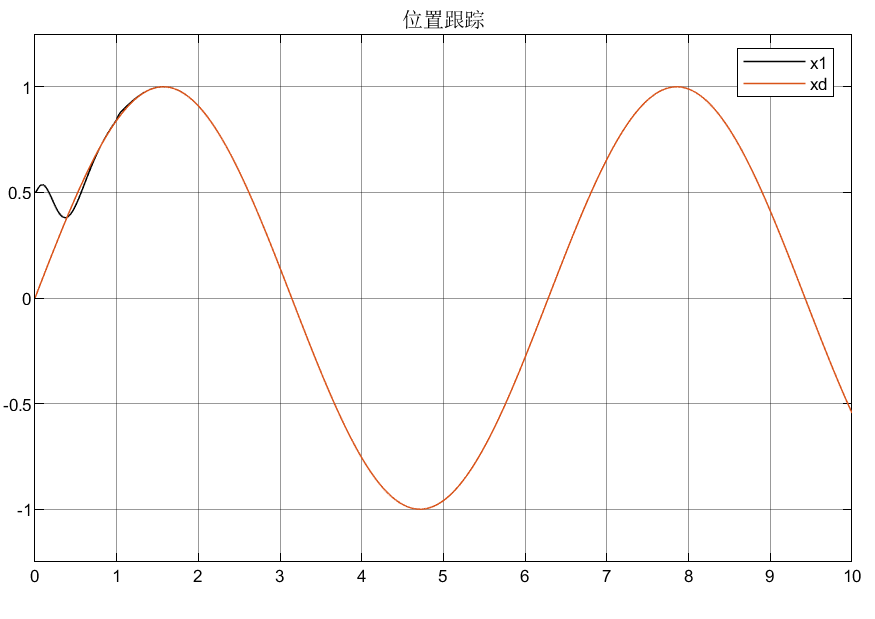
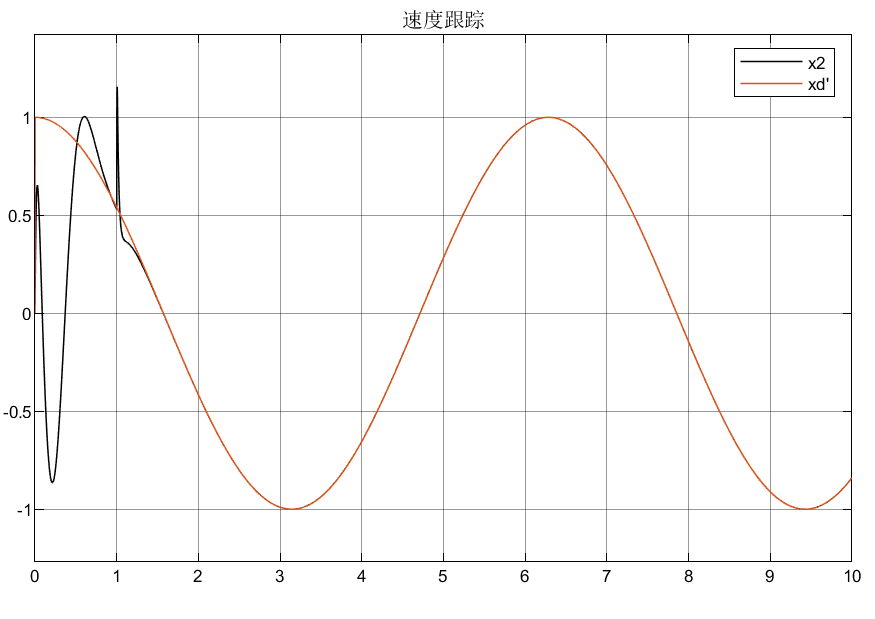
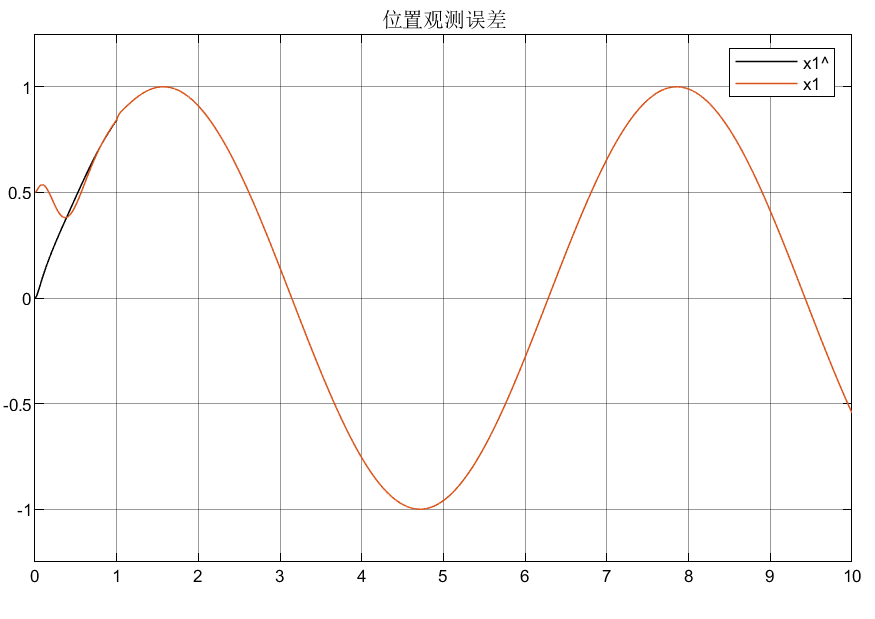
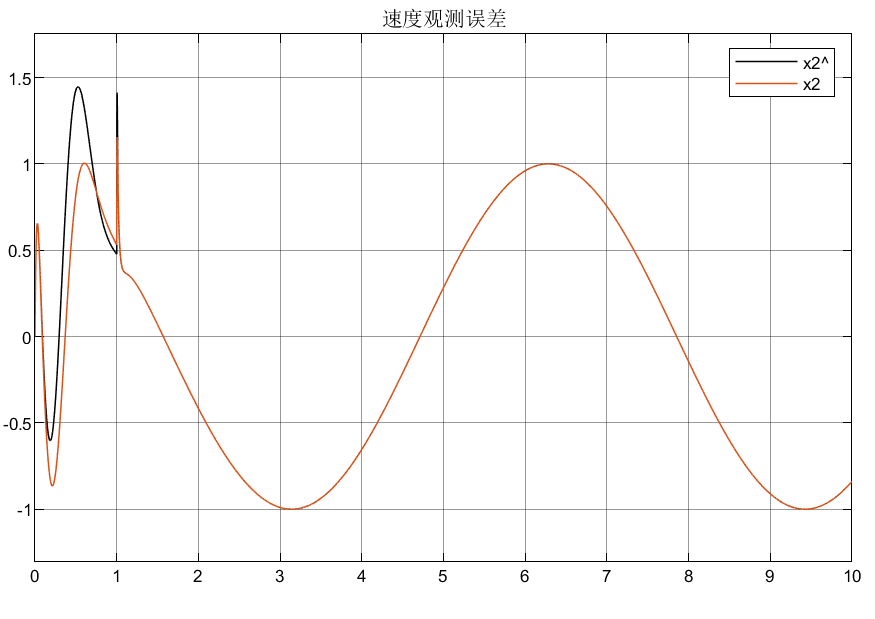
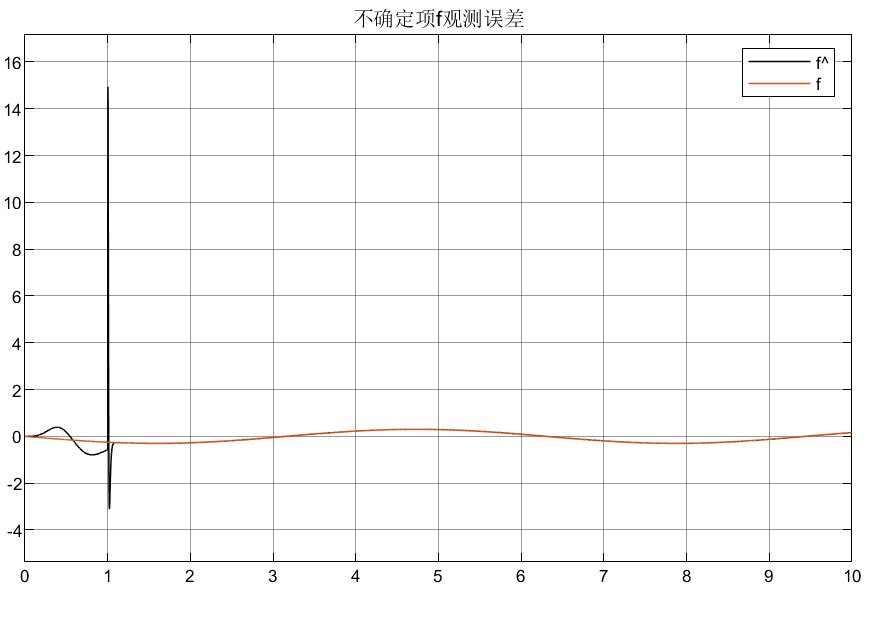
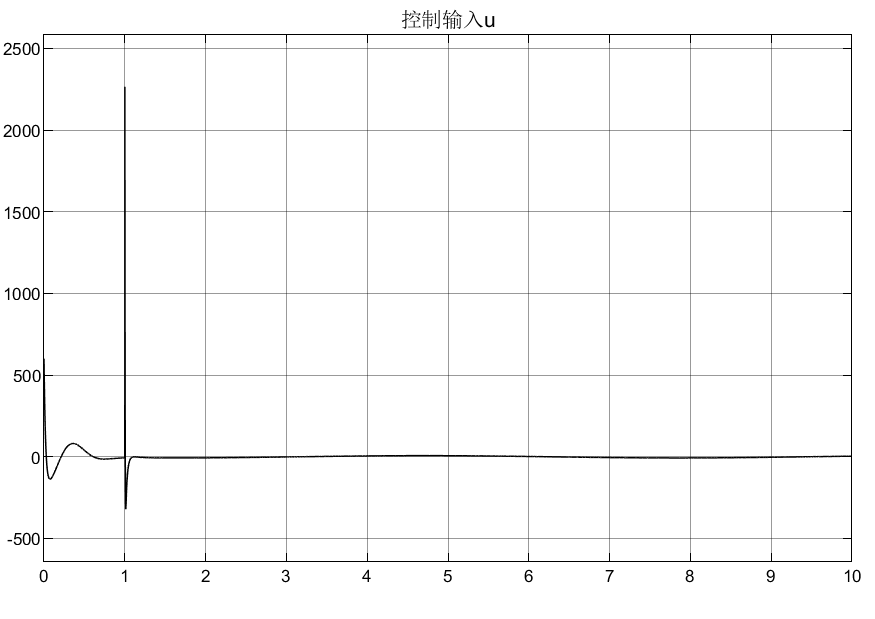
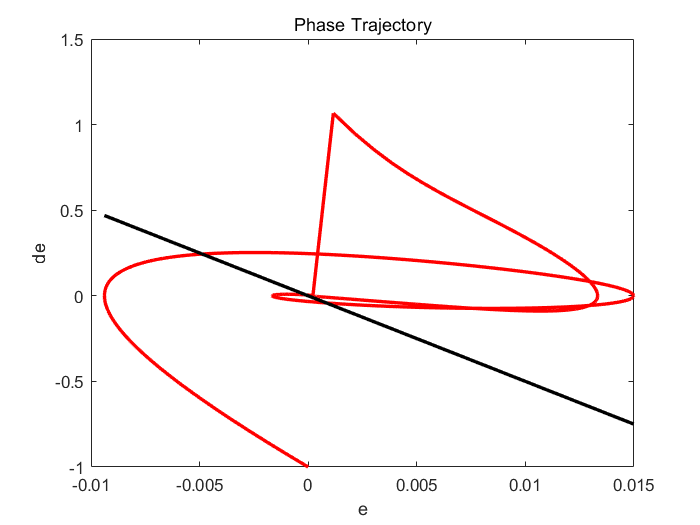
4.3 总结

可以看到相比较普通增益，优化后的自适应增益对初始状态的峰值明显较小，说明了所设计优化增益的合理性。

5 学习问题

①对于Simulink Scope模块的多次使用会导致运算时间长，可以选择使用To Workspace模块将数据输出到工作区间后，使用命令画图。

②所谓的“扩张”指的是扩张了对不确定性项f的估计，把f当成状态变量，所以整体的观测器比被控对象多了一个状态变量f^。

③从相轨迹看稳态误差感觉有些奇怪。

如果有帮助，麻烦帮忙点个赞是我最大的分享动力，非常感谢！

注：仅为便利自己学习，错误在所难免，如有侵权，请联系删除，有兴趣的学者可以参考学习交流，谢谢！

参考资料：

《Nonlinear Control》

最后

以上就是清新衬衫为你收集整理的基于扩张观测器(LESO)的滑模控制前言1 二阶系统LESO观测器设计2.基于LESO的滑模控制器设计​​​​3. 仿真分析(普通高增益项)4. 仿真分析(优化后的高增益项)5 学习问题的全部内容，希望文章能够帮你解决基于扩张观测器(LESO)的滑模控制前言1 二阶系统LESO观测器设计2.基于LESO的滑模控制器设计​​​​3. 仿真分析(普通高增益项)4. 仿真分析(优化后的高增益项)5 学习问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。