图形学基础笔记
【课程主页】GAMES101: 现代计算机图形学入门(2020 年春季)
【B站录播】GAMES101-现代计算机图形学入门-闫令琪
目录
- 图形学基础笔记
- 图形学概述
- 图形学的应用
- Rasterization(光栅化)
- Curves and Meshes
- Ray Tracing
- Animation / Simulation
- 向量与线性代数
- 向量
- 单位向量
- 向量乘法
- 点乘
- 叉乘
- 矩阵
- 变换 Transformation
- 变换矩阵
- 缩放矩阵
- 切变矩阵
- 旋转矩阵
- 齐次坐标
- 引入齐次坐标的原因
- 齐次坐标的引入
- 变换的顺序
- 变换的分解
- 3D旋转
- 观测变换 Viewing transformations
- 观察/相机变换
- 投影变换
- 正交投影 Orthographic Projection
- 透视投影 Perspective Projection
- 光栅化 Rasterization
- 像素(Short for picture element)
- 视口变换
- 成像设备
- 三角形
- 三角形是最基本的形状
- 判断像素与三角形的关系
- 采样 Sampling
- 抗锯齿和深度缓存
- 采样带来的 Artifacts
- 抗锯齿/反走样 Antialiasing
- 频域 Frequency Domain
- 滤波
- 反走样的思想
- 抗锯齿 Antialiasing
- 超分辨率 Supersampling
- 深度缓存 Z-buffer
- 着色 Shading
- 一些基本定义
- Blinn-Phong Model
- 漫反射 Diffuse reflection
- 高光反射 Specular highlights
- 环境光 Ambient lighting
- 着色频率 Shading Frequencies
- Flat Shading
- Gouraud Shading
- Phong Shading
- 渲染管线 pipeline
- 纹理映射 Texture Mapping
- 插值
- 补充:平滑插值
- 重心坐标
- 纹理太小
- 纹理太大
- Mipmap
- 计算 Mipmap 的 Level D
- Mipmap Limitations
- 拓展:在 unity/UE4 中,开启各向异性过滤,纹理内存并不是 3 倍而是 1/3 。
- 纹理应用 Applications of Textures
- 几何 Geometry
- 几何体的表示方式
- 隐式几何 Implicit
- 显式几何 Explicit
- 曲线 Curves
- 计算贝塞尔曲线——de Casteljau 算法
- 逐段贝塞尔曲线 Piecewise Bezier Curves
- 其它曲线:样条 Splines
- 贝塞尔曲面
- 网格操作
- 细分
- Loop Subdivision
- Catmull-Clark Subdivision
- 简化
- 边坍缩
- 阴影 Shadows
- Shadow Mapping
- 阴影的一些问题
- 光照追踪 Ray Tracing
- 为什么需要光照追踪
- Whitted-Style Ray Tracing
- 光线
- Casting Ray:生成 Eye Ray
- Whitted-Style Ray Tracing 思路
- 计算光线和物体表面的交点
- 隐式表面(光线和表达式面)
- 显式表面(光线和三角形)
- 加速求光线和表面的交点
- 加速结构 Acceleration
- 均匀格子 Uniform Grids
- 空间划分 Spatial Partitions
- KD-Tree
- 物体划分 Object Partitions
- Bounding Volume Hierarchy(BVH)
- 辐射度量学 Radiometry
- 辐照强度 Intensity
- 辐[射]照度 Irradiance
- 辐[射]亮度 Radiance
- 双向反射分布函数 BRDF
- 反射方程
- 渲染方程
- 全局光照
- 蒙特卡洛积分与路径追踪
- 蒙特卡洛积分 Monte Carlo Integration
- 路径追踪 Path Tracing
- 俄罗斯轮盘赌 Russian Roulette
- 材质与外观 Materials and Appearances
- 漫反射系数 albedo
- 折射定律 Snell's Law
- 菲涅尔项 Fresnel Reflection / Term
- 微表面材质 Microfacet Material
- 各向同/异性材质 Isotropic / Anisotropic Materials
- BRDF 的性质
- BRDF 的测量
- 高级光线传播 Advanced Light Transport
- 无偏光线传播方法
- 双向路径追踪 Bidirectional Path tPTracing(BDPT)
- Metropolis Light Transport(MLT)
- 有偏光线传播方法
- 光子映射 Photon Mapping
- Vertex Connection and Merging(VCM)
- 实时辐射度算法 Instant Radiosity(IR)
- 高级外观建模 Advanced Appearance Modeling
- 非表面模型 Non-surface Models
- 散射/参与介质 Participating Meida
- 头发/毛发/纤维 Hair / Fur / Fiber(BCSDF)
- 头发
- 毛发
- 颗粒 Granular Material
- 表面模型 Surface Models
- 半透明 Translucent Material(BSSRDF)
- 次表面散射 BSSRDF
- 布料 Cloth
- Detailed Material(non-statistical BRDF)
- 程序化生成模型 Procedural Appearance
- 相机与透镜 Cameras and Lenses
- 视场 Filed of View
- 曝光 Exposure
- 影响曝光度的因素
- 镜头 Lens
- Defocus Blur
- 景深 Depth of Field
- 光场、颜色与感知 Light Field, Color and Perception
- 全光函数 The Plenoptic Function
- 光场 Light Field
- 光场摄像机 Light Field Camera
- 颜色与感知 Color and Perception
- 颜色的物理基础 Physical Basis of Color
- 光谱 Spectrum of Light
- 谱功率密度 Spectral Power Distribution(SPD)
- 三色理论 Tristimulus Theory of Color
- 同色异谱 Metamerism
- 颜色复制和匹配 Color Reproduction / Matching
- 颜色空间 Color Space
- 标准 Standardized RGB(sRGB)
- 通用颜色系统 CIE XYZ
- HSV Color Space
- CMYK:Subtractive Color Space
- 动画与模拟 Animation / Simulation
- 关键帧动画 Keyframe Animation
- 物理模拟 Physical Simulation
- 质点弹簧系统 Mass Spring Rope
- 粒子系统 Particle Systems
- 运动学 Kinematics
- 前向运动学 Forward Kinematics
- 逆向运动学 Inverse Kinematics
- 绑定 Rigging
- 动作捕捉 Motion Capture
- 欧拉方法 Euler's Method
- 中点法 Midpoint Method
- 自适应步长大小 Adaptive Step Size
- 隐式方法 Implicit Method
- **龙格库塔方法** Runge-Kutta Families
- 基于位置的方法 Positon-Based / Verlet Integration
- 刚体模拟 Rigid Body
- 流体模拟 Fluid Simulation
图形学概述
更注重原理,而不是注重 OpenGL、DirectX 等图形API
图形学 ≠ 计算机视觉
// 直白点说,计算机视觉就是猜测分析看到的东西
图形学的应用
- Video Games
- Movies
- Animations
- Design
- Visualization
- Virtual Reality
- Digital illustrations
- Simulation
- Graphical User Interfaces
- Typography
Rasterization(光栅化)
实时图形学的主要应用
// 在计算机图形学中,能达到每秒生成30帧就为“实时”,否则就为“离线”
Curves and Meshes
Ray Tracing
渲染稍微慢一点,目前动画和电影使用较多。当然现在也有一些实时光线追踪的技术
Animation / Simulation
- Key Frame Animation(关键帧动画)
- Mass-spring System
向量与线性代数
基础数学:线性代数、微积分、统计
基础物理:光学、力学
其它知识:信号处理、数值分析、美学
向量
默认都是列向量,这里默认右手坐标系
单位向量
a
^
=
a
⃗
∥
a
⃗
∥
hat{a} = frac{vec{a}}{left | vec{a} right |}
a^=∥a∥a
向量乘法
点乘
- 夹角:点乘除以两向量模长
- 投影:点乘除以投影到向量的模长
- 前后信息:点乘大于0或者小于0
叉乘
- 判断向量左、右关系
a ⃗ × b ⃗ = + z ⃗ vec{a}timesvec{b} = + vec{z} a×b=+z
- 判断内、外
例:已知一个 三角形ABC 和一个 点P,判断点是否在三角形内
分别用AB、BC、CA向量叉乘AP、BP、CP,若三个结果得到的向量通向,则说明AP、BP、CP分别在AB、BC、CA的同一侧,即点P在三角形内
矩阵
两个向量的叉乘可以转换为矩阵乘法
a
⃗
×
b
⃗
=
A
∗
b
=
[
0
−
z
a
y
a
z
a
0
−
x
a
−
y
a
x
a
0
]
⋅
[
x
b
y
b
z
b
]
=
[
y
a
⋅
z
b
−
z
a
⋅
y
b
+
−
x
a
⋅
z
b
+
z
a
⋅
x
b
x
a
⋅
y
b
−
y
a
⋅
x
b
]
vec{a}timesvec{b} = A^*b = begin{bmatrix} 0&-z_a&y_a\ z_a&0&-x_a\ -y_a&x_a&0\ end{bmatrix} cdot begin{bmatrix} x_b\ y_b\ z_b\ end{bmatrix} = begin{bmatrix} y_acdot z_b - z_acdot y_b+\ -x_acdot z_b + z_acdot x_b\ x_acdot y_b - y_acdot x_b\ end{bmatrix}
a×b=A∗b=⎣⎡0za−ya−za0xaya−xa0⎦⎤⋅⎣⎡xbybzb⎦⎤=⎣⎡ya⋅zb−za⋅yb+−xa⋅zb+za⋅xbxa⋅yb−ya⋅xb⎦⎤
变换 Transformation
对于一个把 x 映射到 x’ 的线性变换 T,其中的矩阵 M 就为变换矩阵
T
:
x
′
=
M
x
T: x'=Mx
T:x′=Mx
变换矩阵
缩放矩阵
x 轴缩放 k_x 倍,y 轴缩放 k_y 倍
[
k
x
0
0
k
y
]
begin{bmatrix} k_x&0\ 0&k_y\ end{bmatrix}
[kx00ky]
切变矩阵
x 坐标偏移 y/a
[
1
a
0
1
]
begin{bmatrix} 1&a\ 0&1\ end{bmatrix}
[10a1]
旋转矩阵
旋转 θ 度
[
cos
θ
−
sin
θ
sin
θ
cos
θ
]
begin{bmatrix} cos θ&-sin θ\ sin θ&cos θ\ end{bmatrix}
[cosθsinθ−sinθcosθ]
旋转 -θ 度只需要求其逆矩阵
旋转的逆矩阵 = 旋转的转置 // 正交矩阵
齐次坐标
引入齐次坐标的原因
平移变换不能用矩阵的形式来表示
[
x
′
y
′
]
=
[
1
0
0
1
]
[
x
y
]
+
[
t
x
t
y
]
begin{bmatrix} x'\ y'\ end{bmatrix} = begin{bmatrix} 1&0\ 0&1\ end{bmatrix} begin{bmatrix} x\ y\ end{bmatrix} + begin{bmatrix} t_x\ t_y\ end{bmatrix}
[x′y′]=[1001][xy]+[txty]
平移变换并不属于线性变换,而是仿射变换
// 要考虑 trade off(权衡),为了不让平移称为特例,统一所有的变换,引入齐次变换。但是相对的,代价就是多了一维
齐次坐标的引入
2 D p o i n t = [ x y 1 ] 3 D p o i n t = [ x y z 1 ] 2Dquad point = begin{bmatrix} x\ y\ 1\ end{bmatrix} quad 3D quad point = begin{bmatrix} x\ y\ z\ 1\ end{bmatrix} 2Dpoint=⎣⎡xy1⎦⎤3Dpoint=⎣⎢⎢⎡xyz1⎦⎥⎥⎤
2
D
v
e
c
t
o
r
=
[
x
y
0
]
3
D
v
e
c
t
o
r
=
[
x
y
z
0
]
2Dquad vector = begin{bmatrix} x\ y\ 0\ end{bmatrix} quad 3D quad vector = begin{bmatrix} x\ y\ z\ 0\ end{bmatrix}
2Dvector=⎣⎡xy0⎦⎤3Dvector=⎣⎢⎢⎡xyz0⎦⎥⎥⎤
向量具有平移不变形,即平移后仍然是原向量,所以 w 分量为0
- vector + vector = vector
- point - point = vector
- point + vector = point
而对于 point + point 原本是没有意义的,但是在齐次坐标下,两个点相加就变成了其中点
[
x
1
y
1
w
]
+
[
x
2
y
2
w
]
=
[
x
1
w
y
1
w
1
]
+
[
x
2
w
y
2
w
1
]
=
[
x
1
+
x
2
w
y
1
+
y
2
w
2
]
=
[
x
1
+
x
2
2
y
1
+
y
2
2
w
]
begin{bmatrix} x_1\ y_1\ w\ end{bmatrix} + begin{bmatrix} x_2\ y_2\ w\ end{bmatrix} = begin{bmatrix} frac{x_1}{w}\ frac{y_1}{w}\ 1\ end{bmatrix} + begin{bmatrix} frac{x_2}{w}\ frac{y_2}{w}\ 1\ end{bmatrix} = begin{bmatrix} frac{x_1+x_2}{w}\ frac{y_1+y_2}{w}\ 2\ end{bmatrix} = begin{bmatrix} frac{x_1+x_2}{2}\ frac{y_1+y_2}{2}\ w\ end{bmatrix}
⎣⎡x1y1w⎦⎤+⎣⎡x2y2w⎦⎤=⎣⎡wx1wy11⎦⎤+⎣⎡wx2wy21⎦⎤=⎣⎡wx1+x2wy1+y22⎦⎤=⎣⎡2x1+x22y1+y2w⎦⎤
变换的顺序
复杂的变换是由一系列简单的变换组合而成的
变换的顺序也很重要,这和矩阵的乘法是相关的,因为矩阵乘法不满足交换律,故对于一个复杂变换,先应用缩放,再应用旋转,最后应用平移。
虽然矩阵没有交换律,但是矩阵有结合律,可以将所有变换矩阵相乘为一个矩阵
A
′
=
(
T
⋅
R
⋅
S
⋅
)
A
A' = (Tcdot Rcdot Scdot) A
A′=(T⋅R⋅S⋅)A
变换的分解
假如想要绕着某个点旋转,一个思路是先将锚点平移到坐标原点,旋转后再平移回去。三维空间中绕着某个轴旋转也可以参考这种思路
3D旋转
欧拉角α、β、γ
R
x
y
z
=
R
x
(
α
)
R
y
(
β
)
R
z
(
γ
)
R_{xyz} = R_x(alpha)R_y(beta)R_z(gamma)
Rxyz=Rx(α)Ry(β)Rz(γ)
四元数
四元数由四部分组成,一个实部,三个虚部
q
^
=
(
q
v
^
,
q
w
^
)
=
i
q
x
+
j
q
v
+
k
q
z
+
q
w
hat{q} = (hat{q_v}, hat{q_w}) = iq_x + jq_v + kq_z + q_w
q^=(qv^,qw^)=iqx+jqv+kqz+qw
平滑插值
观测变换 Viewing transformations
观察/相机变换
相机的位置 e、相机的朝向 g、相机向上的方向 t
M
v
i
e
w
=
R
v
i
e
w
T
v
i
e
w
M_{view} = R_{view}T_{view}
Mview=RviewTview
先平移到原点
T
v
i
e
w
=
[
1
0
0
−
x
e
0
1
0
−
y
e
0
0
1
−
z
e
0
0
0
1
]
T_{view} = begin{bmatrix} 1 & 0 & 0 & -x_e\ 0 & 1 & 0 & -y_e\ 0 & 0 & 1 & -z_e\ 0 & 0 & 0 & 1\ end{bmatrix}
Tview=⎣⎢⎢⎡100001000010−xe−ye−ze1⎦⎥⎥⎤
观察/相机变换就是将相机移动到原点,朝向 -z 看的过程
要想把相机的三个轴 g、t、(gxt) 分别旋转到 -z、y、x 并不容易,考虑反向旋转,即
R
v
i
e
w
−
1
=
[
x
g
^
×
t
^
x
t
x
−
g
0
y
g
^
×
t
^
y
t
y
−
g
0
z
g
^
×
t
^
z
t
z
−
g
0
0
0
0
1
]
R^{-1}_{view} = begin{bmatrix} x_{hat{g}times hat{t}}&x_t& x_{-g} &0\ y_{hat{g}times hat{t}}&y_t& y_{-g} &0\ z_{hat{g}times hat{t}}&z_t& z_{-g} &0\ 0&0&0&1\ end{bmatrix}
Rview−1=⎣⎢⎢⎡xg^×t^yg^×t^zg^×t^0xtytzt0x−gy−gz−g00001⎦⎥⎥⎤
又因为对旋转矩阵求逆就等于对旋转矩阵求转置,故
R
v
i
e
w
=
[
x
g
^
×
t
^
y
g
^
×
t
^
z
g
^
×
t
^
0
x
t
y
t
z
t
0
x
−
g
y
−
g
z
−
g
0
0
0
0
1
]
R_{view} = begin{bmatrix} x_{hat{g}times hat{t}}&y_{hat{g}times hat{t}} & z_{hat{g}times hat{t}} & 0\ x_t & y_t & z_t & 0\ x_{-g} & y_{-g}&z_{-g}&0\ 0&0&0&1\ end{bmatrix}
Rview=⎣⎢⎢⎡xg^×t^xtx−g0yg^×t^yty−g0zg^×t^ztz−g00001⎦⎥⎥⎤
投影变换
正交投影 Orthographic Projection
把一个长方体 [l, r] x [b, t] x [f, n] 映射到一个标准立方体(Canonical Cube)
// 因为摄像机是看向 -z 轴的,所以 far 比 near 的数值要小
M
o
r
t
h
o
=
[
2
r
−
l
0
0
0
0
2
t
−
b
0
0
0
0
2
n
−
f
0
0
0
0
1
]
⋅
[
1
0
0
−
r
+
l
2
0
1
0
−
t
+
b
2
0
0
1
−
n
+
f
2
0
0
0
1
]
M_{ortho} = begin{bmatrix} frac{2}{r-l} & 0 & 0 & 0\ 0 & frac{2}{t-b} & 0 & 0\ 0 & 0 & frac{2}{n-f} & 0\ 0 & 0 & 0 & 1\ end{bmatrix} cdot begin{bmatrix} 1 & 0 & 0 & -frac{r+l}{2}\ 0 & 1 & 0 & -frac{t+b}{2}\ 0 & 0 & 1 & -frac{n+f}{2}\ 0 & 0 & 0 & 1\ end{bmatrix}
Mortho=⎣⎢⎢⎡r−l20000t−b20000n−f200001⎦⎥⎥⎤⋅⎣⎢⎢⎡100001000010−2r+l−2t+b−2n+f1⎦⎥⎥⎤
透视投影 Perspective Projection
思路:先把透视空间的 截头锥体(Frustum) 挤压成一个长方体,再利用正交的方法进行投影
对于任一点 (x, y, z),由相似三角形可得到关系
y
′
=
n
z
⋅
y
x
′
=
n
z
⋅
x
y' = frac{n}{z}cdot y quad x' = frac{n}{z}cdot x
y′=zn⋅yx′=zn⋅x
在齐次坐标中由上面关系可得,(x, y, z, 1) 经过一个变换后得到(nx/z, ny/z, unknown, 1),即(nx, ny, unknown, z),那么可推出
M
p
e
r
s
p
→
o
r
t
h
o
=
[
n
0
0
0
0
n
0
0
?
?
?
?
0
0
1
0
]
M_{persp to ortho} = begin{bmatrix} n & 0 & 0 & 0\ 0 & n & 0 & 0\ ? & ? & ? & ?\ 0 & 0 & 1 & 0\ end{bmatrix}
Mpersp→ortho=⎣⎢⎢⎡n0?00n?000?100?0⎦⎥⎥⎤
在近平面 Near 上的点的 z 挤压后值不变,可得
[
0
0
A
B
]
⋅
[
x
y
n
1
]
=
n
2
begin{bmatrix} 0 & 0 & A & B end{bmatrix} cdot begin{bmatrix} x\y\n\1 end{bmatrix} = n^2
[00AB]⋅⎣⎢⎢⎡xyn1⎦⎥⎥⎤=n2
在远平面 Far 的中心点(0, 0, f) 挤压后仍然是(0, 0, f),可得
[
0
0
A
B
]
⋅
[
x
y
f
1
]
=
f
2
begin{bmatrix} 0 & 0 & A & B end{bmatrix} cdot begin{bmatrix} x\y\f\1 end{bmatrix} = f^2
[00AB]⋅⎣⎢⎢⎡xyf1⎦⎥⎥⎤=f2
由方程组可解出A、B
KaTeX parse error: Unknown column alignment: 2 at position 24: … begin{array}{2̲} An + B = n^2 …
最后再加上正交投影可得最后的透视投影矩阵
M
p
e
r
s
p
=
M
o
r
t
h
o
M
p
e
r
s
p
→
o
r
t
h
o
M_{persp}=M_{ortho}M_{persp to ortho}
Mpersp=MorthoMpersp→ortho
光栅化 Rasterization
正交或透视投影已经将物体映射到了 -1到1 的正方体内,下一步 光栅化Rasterization 就是要 drawing onto the screen
像素(Short for picture element)
假定以左下角为原点,像素的坐标从 (0, 0) 到 (width - 1, height - 1),但是像素的中心在 (x + 0.5, y + 0.5)
视口变换
先不管 z 轴,只是简单的将 -1到1 的正方体映射到屏幕空间
M
v
i
e
w
p
o
r
t
=
w
i
d
t
h
2
0
0
w
i
d
t
h
2
0
h
e
i
g
h
t
2
0
h
e
i
g
h
t
2
0
0
1
0
0
0
0
1
M_{viewport} = begin{matrix} frac{width}{2} & 0 & 0 &frac{width}{2}\ 0 & frac{height}{2} & 0 & frac{height}{2}\ 0 & 0 & 1 & 0\ 0 & 0 & 0 & 1\ end{matrix}
Mviewport=2width00002height0000102width2height01
成像设备
- 示波器 Oscilipscope
- 阴极射线管
- 帧缓存
- 平板显示设备 Flat Panel
- 液晶显示器 LCD
- 发光二极管 LED
- 有机发光二极管 OLED
- 超视网膜 XDR
- 电子墨水屏 Electronic Ink
三角形
三角形是最基本的形状
- 最基本的多边形
- 可以拆分其它多边形为三角形
- 独特的性质
- 三点所构成的三角形一定在一个面
- 很好定义内外部
- 很好定义插值的方法(已知三个顶点的属性,三角形里的属性可以通过插值求得)
判断像素与三角形的关系
采样 Sampling
采样就是将函数离散化的过程。在光栅化中,就是利用像素中心对屏幕进行采样,即判断像素的中心点是否在三角形内部来决定该像素是否渲染
int inside(t, x, y)
{
if( //中心点在三角形内部 )
return 1;
else
return 0;
}
void Sampling(*args)
{
for (int x = 0; x < xmax; ++x)
for(int y = 0; y < ymax; ++y)
{
image[x][y] = inside (tri, x + 0.5, y + 0.5);
}
}
判断方法:
- 三次叉乘通向
- 过中心点做射线与三角形仅有一个交点
- 连接中心点与三个顶点构成三个三角形面积和与原三角形相等
使用三角形的 包围盒Bounding Box,减少遍历的像素点数
抗锯齿和深度缓存
采样带来的 Artifacts
不只是位置上可以采样,时间上也可以采样,例如动画或者视频,实际上,并没有连续意义上的动画。采样是广泛存在的,同样的,采样产生的问题也是广泛存在的。在图形学中把采样带来的各种问题 (Errors / Mistakes / Inaccuracies)统称为 **Artifacts **
- 锯齿(Jaggies)
- 摩尔纹(Moire Patterns)
- 车轮效应(Wagon Wheel Effect):时间采样问题
Artifacts 产生的原因可简单总结为:信号的速度太快而采样速度跟不上
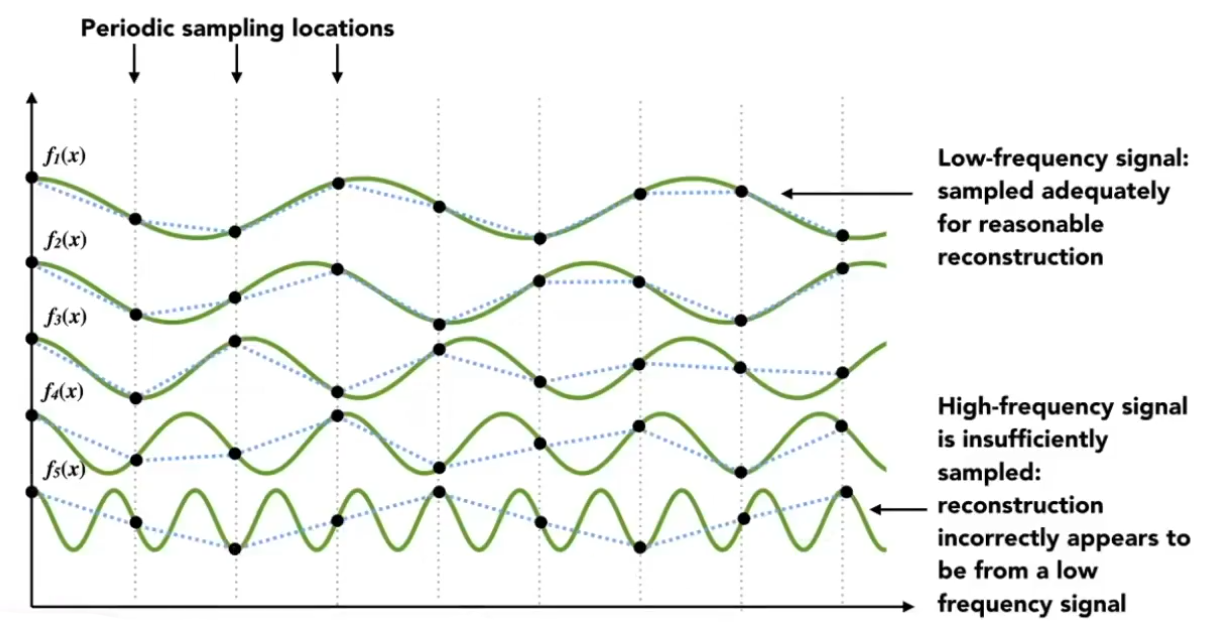
抗锯齿/反走样 Antialiasing
在采样前做 Blurring(Pre-Filtering),即先做模糊再采样
频域 Frequency Domain
傅里叶级数展开:任何周期函数都可以写出一系列正弦和余弦的线性组合加上常数项
傅里叶变换: 任何函数表示成另一个函数
f
(
x
)
⇔
F
(
x
)
f(x)Leftrightarrow F(x)
f(x)⇔F(x)
傅里叶变换的思想是,逐渐使用高频采样,以无限逼近原始函数。
频域的自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。可以对图像经傅立叶变换后的频谱成分进行处理,然后逆傅立叶变换获得所需的图像
滤波
高通滤波:过滤掉低频,剩下轮廓
低通滤波:过滤掉高频
滤波(Flitering) = 平均(Averaging) = 卷积(Convolution)
// 时域上的乘积 = 频域上的卷积
反走样的思想
先做模糊(低通滤波),再采样
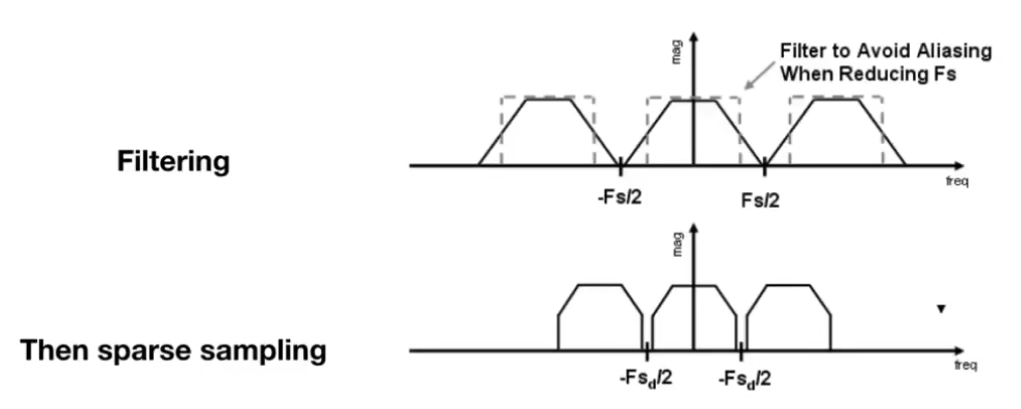
抗锯齿 Antialiasing
- MSAA
将一个像素逻辑上分为更小的像素,判断各小像素中心点是否在三角形,计算出每个像素的近似覆盖率
- FXAA(Fast Approximate AA)
是一种单纯的图像后期处理,得到锯齿图再处理。核心思路有两点:边缘判定算法、边缘像素混合因子计算
- TAA(Temporal AA)
找上一帧的结果
超分辨率 Supersampling
- DLSS(Deep Learning Super Sampling)
深度缓存 Z-buffer
在深度中假设 z 值都是正值,即越小的 z 值代表者离镜头越近,越大的 z 值离镜头越远
深度缓存思路:为每个像素存储当前最小的 z 值
for (each trangle T)
for(each sample(x, y, z) in T)
{
if(z < zbuffer[x, y]) // 当前最近的点
{
framebuffer[x, y] = rgb; // 更新颜色
zbuffer[x, y] = z; // 更新深度
}
else
;
}
着色 Shading
在图形学中,Shading 就是对不同的物体应用不同 材质Material 的过程。
着色是局部的,不考虑其它物体的存在,例如其它物体投射的阴影
一些基本定义
对于物体表面的一个 Shading Point,在可认为是一个极小的平面。定义以下单位向量
- 法线(Normal)
n - 观测方向(Viewer direction)
v - 光照方向(Light direction)
l
Blinn-Phong Model
经验模型,并不完全符合真实世界中的关照现象
KaTeX parse error: No such environment: align at position 7: begin{̲a̲l̲i̲g̲n̲}̲ L & = L_a + L_…
- 环境光 Ambient lighting
- 漫反射 Diffuse reflection
- 高光反射 Specular highlights
漫反射 Diffuse reflection
反射光线的强度与表面法线和光源方向之间夹角的余弦值成正比,由于都是单位向量,故 cosθ = n·l
KaTeX parse error: No such environment: align at position 7: begin{̲a̲l̲i̲g̲n̲}̲ L_d & = k_d(f…
k_d:漫反射系数(diffuse coefficient),用于颜色
I/r^2:到达着色点的能量
高光反射 Specular highlights
当镜面反射和观察方向接近时,会出现高光向
Bling-Phong 模型相较于 Phong 模型的改进是将判断镜面反射 R 和观察方向 v 改为判断法向方向 n 和半程向量 h
h
=
b
e
s
e
c
t
o
r
(
v
,
l
)
=
v
+
l
∥
v
+
l
∥
h = besector(v, l) = frac{v+l}{left | v+l right |}
h=besector(v,l)=∥v+l∥v+l
n 和 h 足够接近就表示能够看到高光
KaTeX parse error: No such environment: align at position 7: begin{̲a̲l̲i̲g̲n̲}̲ L_s & = k_s(f…
k_s:高光反射系数,通常是白色
h:半程向量,l 和 v 角平分线方向的单位向量
p:余弦函数的容忍度太高了,该指数用于收缩高光范围。// 在 bling-phong 模型中该指数一般设为 100~200
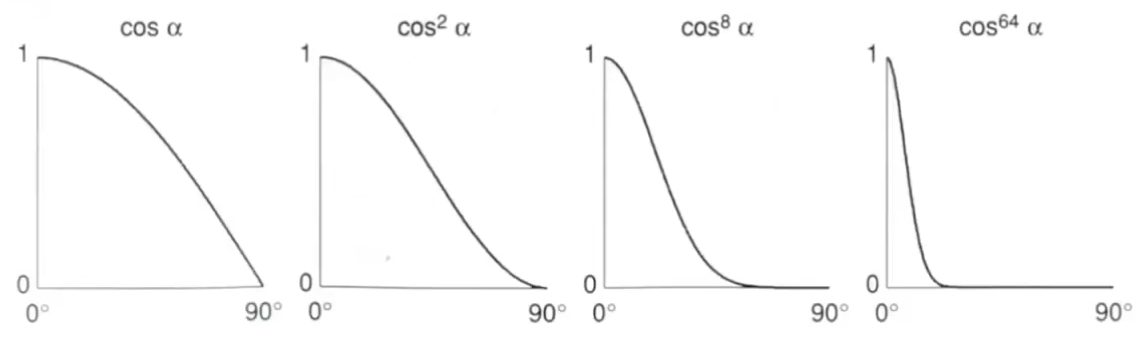
环境光 Ambient lighting
认为来自环境光的光强都一样,近似得到环境光
L
a
=
k
a
I
a
L_a = k_aI_a
La=kaIa
着色频率 Shading Frequencies
Flat Shading
对每个三角形 triangle 着色,也就是在一个三角形内的颜色都是一致的
Gouraud Shading
对每个顶点 vertex 求出法线,每个顶点做一次着色,三角形内部通过插值的方式着色。
求顶点法线方向的思路就是对相邻面的法线求平均,当然也可以求加权平均
N
v
=
∑
i
N
i
∥
∑
i
N
i
∥
N_v = frac{sum_{i}N_i}{left | sum_{i}N_i right| }
Nv=∥∑iNi∥∑iNi
Phong Shading
对每个像素 pixel 由之前顶点的法线插值出三角形内像素的法线,对每个像素着色
渲染管线 pipeline
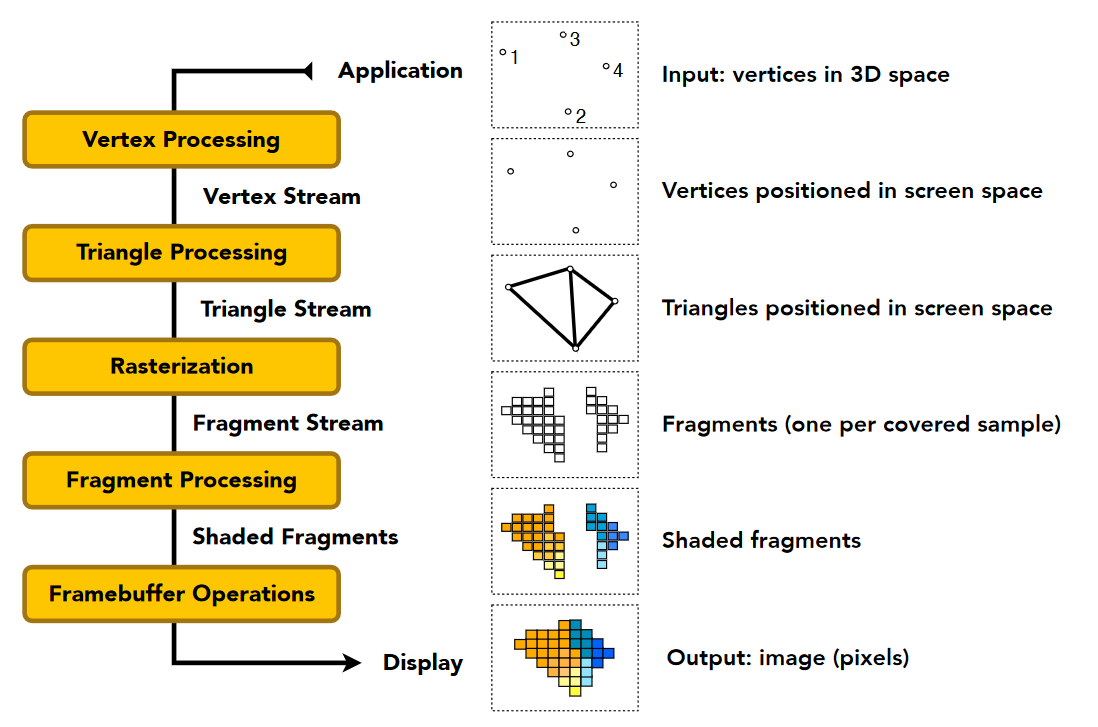
着色在顶点和像素处理部分都可以进行
纹理映射 Texture Mapping
纹理可以定义任何一个点的基本属性,比如颜色(漫反射系数)
不管 uv 的形状、长宽比如何,uv 的值都在 [0, 1]
插值
为什么插值:指定顶点的值或三角形内获取光滑的值
插值的内容:纹理插值、颜色、法向
补充:平滑插值
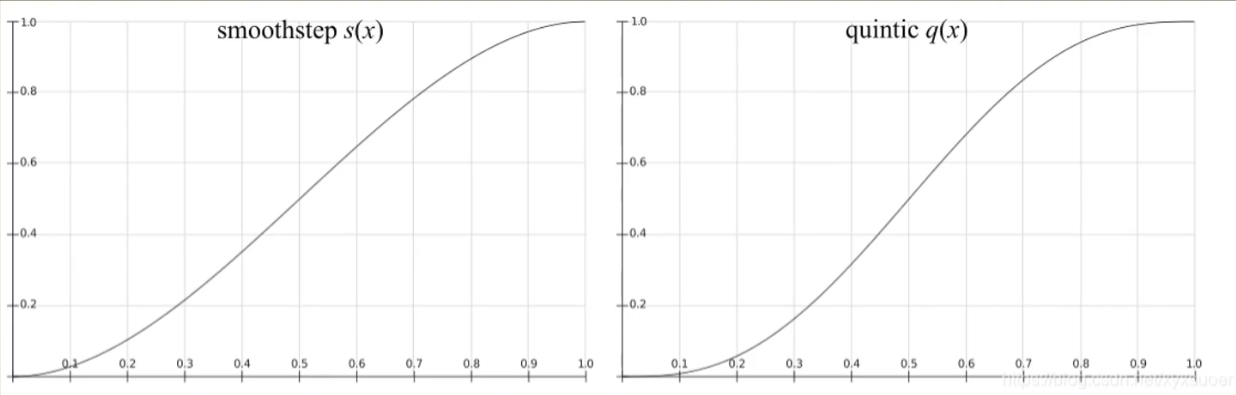
平滑插值
s
(
x
)
=
x
2
(
3
−
2
x
)
quintic插值
q
(
x
)
=
x
3
(
6
x
2
−
15
x
+
10
)
text{平滑插值} quad s(x) = x^2(3-2x) \ text{quintic插值} quad q(x) = x^3(6x^2-15x+10)
平滑插值s(x)=x2(3−2x)quintic插值q(x)=x3(6x2−15x+10)
重心坐标
重心坐标是插值的基础,uv 用顶点坐标存储,中间的片元通过插值求得
三角形所在平面内任一点都可以用三角形坐标系(α, β, γ)来表示
(
x
,
y
)
=
α
A
+
β
B
+
γ
C
(x, y) = alpha A+beta B +gamma C
(x,y)=αA+βB+γC
对于重心来说,重心坐标只需要满足如下条件,即 α = β = γ = 1/3
α
+
β
+
γ
=
1
alpha+beta+gamma = 1
α+β+γ=1
但是由于重心在投影之后会发生变化,所以为了准确插值应该在三维空间中求重心。
纹理太小
由于纹理是映射的,如果纹理太小可能映射到一个非整数的点上
- 最近邻 Nearest
- 双线性插值 Bilinear
找到临近的四个像素的中心点,进行插值
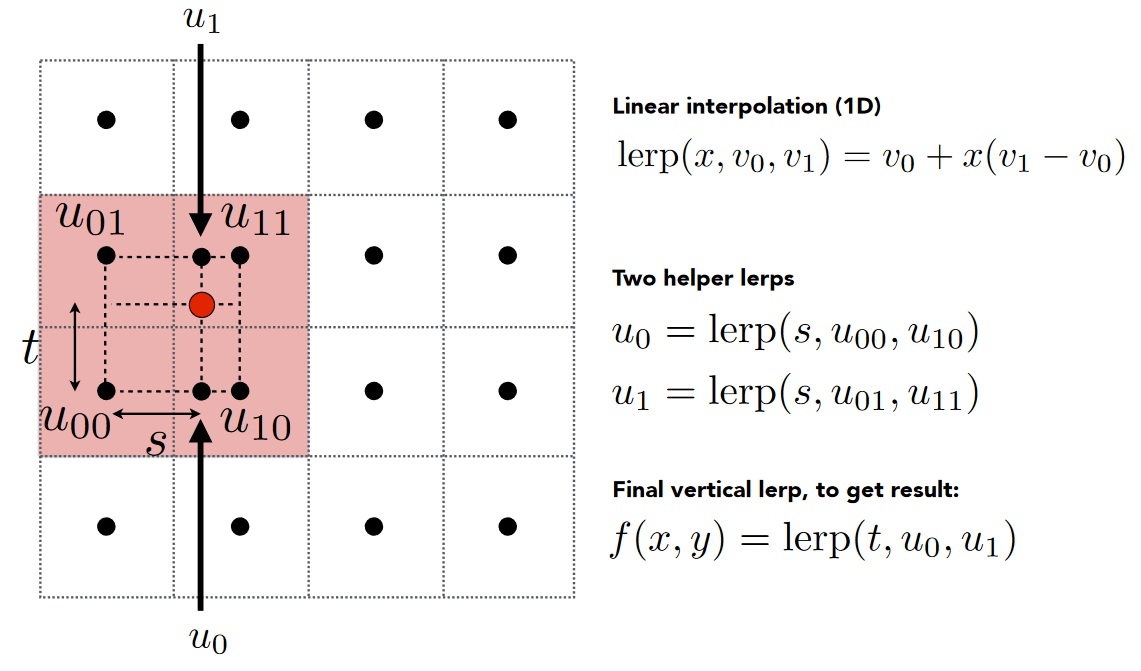
- 立方卷积 Bicubic
找到临近的16个像素的中心点,进行插值
卷积插值公式:
W
(
x
)
=
{
(
a
+
2
)
∣
x
∣
3
−
(
a
+
3
)
∣
x
∣
2
+
1
,
∣
x
∣
≤
1
a
∣
x
∣
3
−
5
a
∣
x
∣
2
+
8
a
∣
x
∣
−
4
a
,
1
<
∣
x
∣
<
2
0
,
otherwise
W(x) = begin{cases} (a+2){left| x right|}^3-(a+3){left| x right|}^2+1, & {left| x right|}leq 1 \ a{left| x right|}^3-5a{left| x right|}^2+8a{left| x right|}-4a, & 1<{left| x right|}<2 \ 0, & text{otherwise} end{cases}
W(x)=⎩⎪⎨⎪⎧(a+2)∣x∣3−(a+3)∣x∣2+1,a∣x∣3−5a∣x∣2+8a∣x∣−4a,0,∣x∣≤11<∣x∣<2otherwise
纹理太大
可类比采样速度跟不上,会导致锯齿,摩尔纹
// 纹理太小可理解为多个像素对应一个纹理,纹理太大则是一个像素要显示多个纹理的信息
// 涉及到算法和数据结构:点查询问题(给一个点求它的值是多少:双线性插值)和范围查询问题(给你一个区域求它的平均值)
Mipmap
允许快速、近似、方块做范围查询
mipmap的额外内存开销:1/3
计算 Mipmap 的 Level D
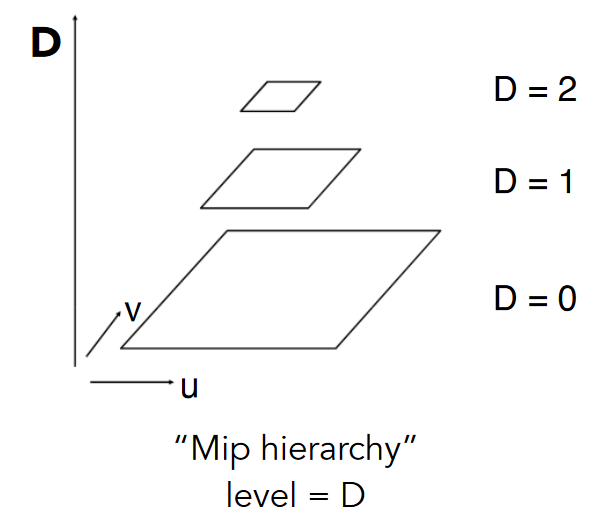
计算像素在 mipmap 的哪一层
D
=
log
2
L
D = log_2 L
D=log2L
对于中间的层数,可通过插值得到
float dx = ddx(i.uv); // GPU并不是逐像素而是分块2x2。这样方便计算偏导数
float dy = ddy(i,uv);
float lod = 0.5 * log2(max(dot(dx, dx), dot(dy, dy)));
float albedo = tex2Dlod(_MainTex, float4(i.uv, 0, lod)).rgb;
Mipmap Limitations
因为 mipmap 只能做方块的查询,所以也会有一些问题,比如 Overblur ,即在远处会模糊丢失细节。
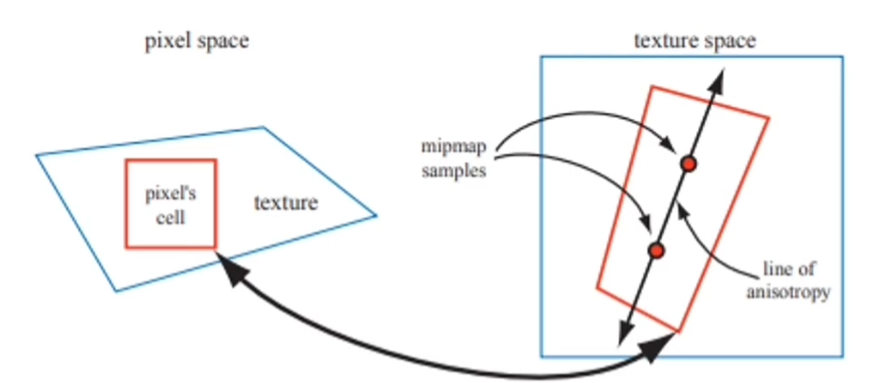
部分解决三线性插值的问题:各向异性过滤 Anisotropic Filtering
各向异性比三线性插值等比缩放多了沿着两个轴的对应缩放,映射回到原图时就是一个长方形,可以解决部分问题,但代价是额外内存是原来的三倍

但对于其它多边形,比如斜着的矩形,仍然效果不好,所以还有进一步的解决办法,EWA Filtering 用椭圆过滤,同样的,代价是消耗能多的内存。
拓展:在 unity/UE4 中,开启各向异性过滤,纹理内存并不是 3 倍而是 1/3 。
原理是通过屏幕像素反向投影到纹理空间形成的不规则四边形取最短边(Mipmap使用最长边)较长的边的方向为各向异性方向,按照过滤等级高低进行多次采样合成得到最后的结果。
与前面的区别可理解为前面通过算法选择使用最合适 Mimap 图。后者是通过屏幕投射而去判定选择那一张 Mimap 图,计算消耗比较高
纹理应用 Applications of Textures
可以把纹理理解为内存 + 范围查询(过滤)
- 环境光照
环境光默认无穷远,,只需要知道环境光的方向就可以,可以将环境光记录在一个球上 Spherical Environment Map,展开后可以得到原图
- 凹凸贴图
除了颜色,贴图也可以定义点的相对高度,在不把几何体变复杂的情况下通过将贴图精细化达到低模渲染高模的效果
// 实质上是通过法线变化达到着色变化,实现凹凸效果的
通过凹凸贴图定义模拟的切线,通过切线计算法线
假设 2D 中原始法线为 (0, 1),3D 中原始法线为 (0, 0, 1)
2
D
n
=
(
−
d
p
,
1
)
.
n
o
r
m
a
l
i
z
e
d
(
)
3
D
n
=
(
−
d
p
d
u
,
−
d
p
d
v
,
1
)
.
n
o
r
m
a
l
i
z
e
d
(
)
2D quad n = (-dp,1).normalized()\ 3D quad n = (-frac{dp}{du}, -frac{dp}{dv}, 1).normalized()
2Dn=(−dp,1).normalized()3Dn=(−dudp,−dvdp,1).normalized()
- 位移贴图
凹凸贴图由于是计算假的法线达到的视觉效果所以在某些情况下会露馅,比如边缘和阴影。位移贴图会真正的移动顶点,但是要求模型精细度很高
// 发散思维:DirectX 提供动态细分的API,即一个低模先应用位移贴图,在检测过程中需要细分的时候在进行曲面细分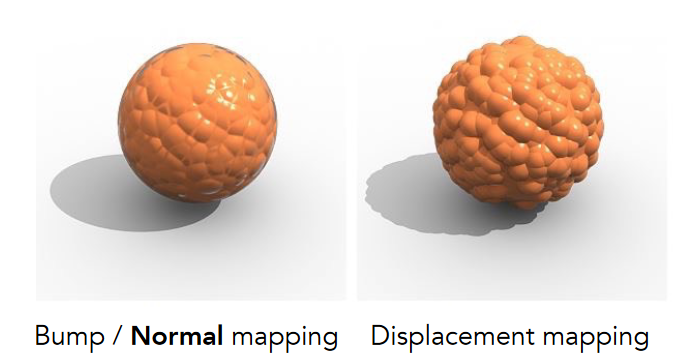
- 3D Proceduarl Noise
利用三维空间中的噪声函数,经过一定处理得到固体模型
- 提供预着色 Provide Precomputed Shading
可以用纹理记录一些已经计算好的信息。比如 Simple shading 后,可以写进一张环境光遮蔽贴图,再将着色结果乘以环境光遮蔽得到最终的结果。
- 三维材质和体积渲染 3D Textures and Volume Rendering
几何 Geometry
几何体的表示方式
隐式几何 Implicit
- 只说明点满足的一些特殊关系,不说明具体点的位置
// E.g. sphere: all points in 3D, where x2+y2+z^2= 1
- 通过布尔运算组合隐式几何体 CSG(Constrctive Solid Geometry)
- 距离函数
不直接描述表面,而是描述任何一个点到这个表面的最近距离
- 分型
显式几何 Explicit
- 说明点的具体位置
- 通过参数映射的方式表示(可以把 x, y, z 用其它参数表示出来)
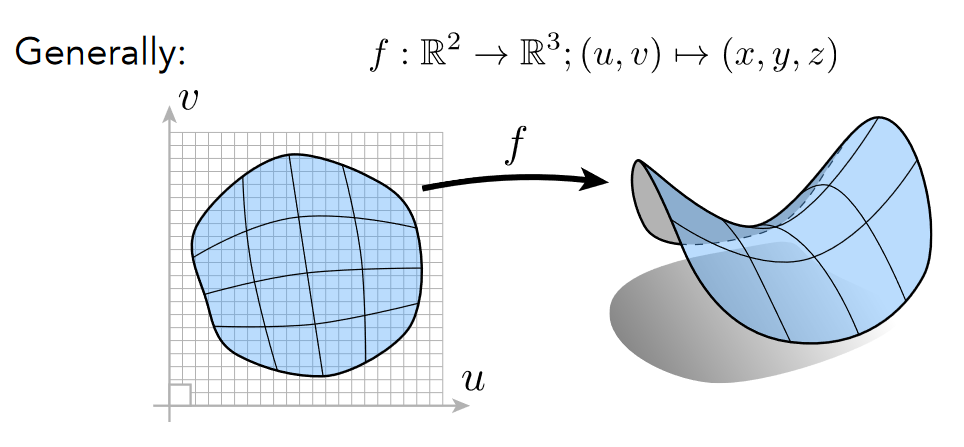
- 点云 Point Cloud
list of points(x, y, z)
- 多边形面 Polygon Mesh
通常是 triangle or quads
- 曲线 Curves
贝塞尔曲线:通过一系列点(起止点和控制点)定义一条曲线
曲线 Curves
计算贝塞尔曲线——de Casteljau 算法
思路:把线段分成多段,每一段[0, 1],不断地线性插值迭代得到 t 分位的点的位置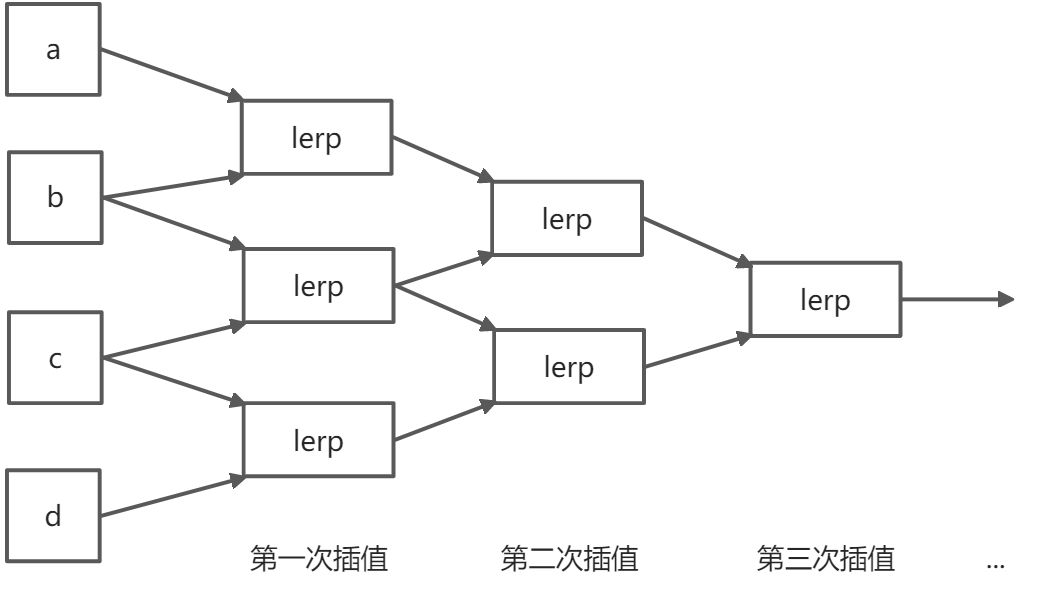
数学上的逻辑可以用公式表示
b
n
(
t
)
=
b
0
n
(
t
)
=
∑
j
=
1
n
b
j
B
j
n
(
t
)
b^n(t) = b_0^n(t) = sum_{j=1}^n b_jB_j^n(t)
bn(t)=b0n(t)=∑j=1nbjBjn(t)
表示 n+1 个控制点得到的 n 阶贝塞尔曲线,在任意分位 t 的点的位置是控制点的线性组合,系数是一个二项分布多项式
贝塞尔曲线的性质:
- 对控制点做仿射变换后再求出的贝塞尔曲线和对已求得的贝塞尔曲线做仿射变换得到曲线是等价的(仿射变换才是等价的,投影变换不适用)
- 凸包性质,贝塞尔曲线一定在控制点的凸包内
逐段贝塞尔曲线 Piecewise Bezier Curves
每四个点(起止点+两个控制点)定义一条贝塞尔曲线。 // 钢笔工具
其它曲线:样条 Splines
对于贝塞尔曲线,移动一个控制点的位置,整条曲线都会移动,有时候并不是我们想要的结果,我们先想要一种“局部性”可控的曲线,样条采用加权平均可实现。 // 类似衰减编辑
贝塞尔曲面
4x4 个点定义一个曲面
网格操作
- 网格细分 subdivision
- 网格简化 simlification
- 网格正规化 regularization
细分
Loop Subdivision
// Loop是人名,这里不是循环的意思
不仅要拆分三角形,还要对顶点调整位置。
对于细分出的新顶点,一定在一条边上,这条边被两个三角形所共享,这条边上原来三角形的顶点为A、B,不在这边上原来三角形顶点为C、D,那么新的顶点的位置为加权平均:
3
8
(
A
+
B
)
+
1
8
(
C
+
D
)
frac{3}{8}(A+B)+frac{1}{8}(C+D)
83(A+B)+81(C+D)
对于旧的三角形顶点
n:顶点的度,即连接的边的数量
u:3/16 if n=3, 3/8n otherwise
那么旧顶点的新位置为:
(
1
−
n
×
u
)
×
o
r
i
g
i
n
a
l
_
p
o
s
i
t
i
o
n
+
u
×
n
e
i
g
h
b
o
r
_
p
o
s
i
t
i
o
n
_
s
u
m
(1-ntimes u)times original_position+ utimes neighbor_position_sum
(1−n×u)×original_position+u×neighbor_position_sum
Catmull-Clark Subdivision
四边形面 quad face
非四边形面 non-quad face
奇异点 extraordinary vertex:度不为4的点
做完第一次细分后,会增加非四边形面数的奇异点,非四边形面消失,之后再细分也不再增加奇异点数量。
$Face Point: quad f = frac{v_1+v_2+v_3+v_4}{4}
Edge Point: quad e = frac{v_1+v_2+f_1+f_2}{4}
Vertex Point: quad v = frac{f_1+f_2+f_3+f_4+2(m_1+m_2+m_3+m_4+4p)}{16}$
其中,m 是边的中点,p 是旧的 vertex point
简化
边坍缩
通过二次误差度量(Quadric Error Metrics)来衡量对那些边进行坍缩。 // 优先队列:求最小,并且动态更新
阴影 Shadows
Shadow Mapping
思想:如果点不在阴影里,那么可以从摄像机视角和光源看到这个点;如果点在阴影里,那么从摄像机视角里可以看到点但是光源看不到这个点
- 从光源看,记录下深度信息
- 从摄像机里看,投影回光源,如果深度一致,则是明亮处;如果不一致,则是阴影处
阴影的一些问题
- 硬阴影
- 质量依靠于分辨率
- 浮点精度等问题
光照追踪 Ray Tracing
为什么需要光照追踪
光栅化不能很好的处理全局的效果,例如软阴影和多次的光线反射
光栅化很快速,但是真实性很低
光照追踪很精确,但是很慢
Whitted-Style Ray Tracing
光线
关于光线的一些 ideas:
- 光线沿直线传播
- 光线之间不会发生碰撞
- 光线从光源出发,最后到达观察者的眼睛,该过程可逆找到光路
Casting Ray:生成 Eye Ray
观察点和想象的待渲染平面的点连线,与场景物理的交点和光源连线判断是否被光源照亮,对其着色渲染到像素
Whitted-Style Ray Tracing 思路
通过多次反射和折射达到光线追踪的效果,例如,对于一个玻璃球,eye ray 打上去时要进行一次反射和折射
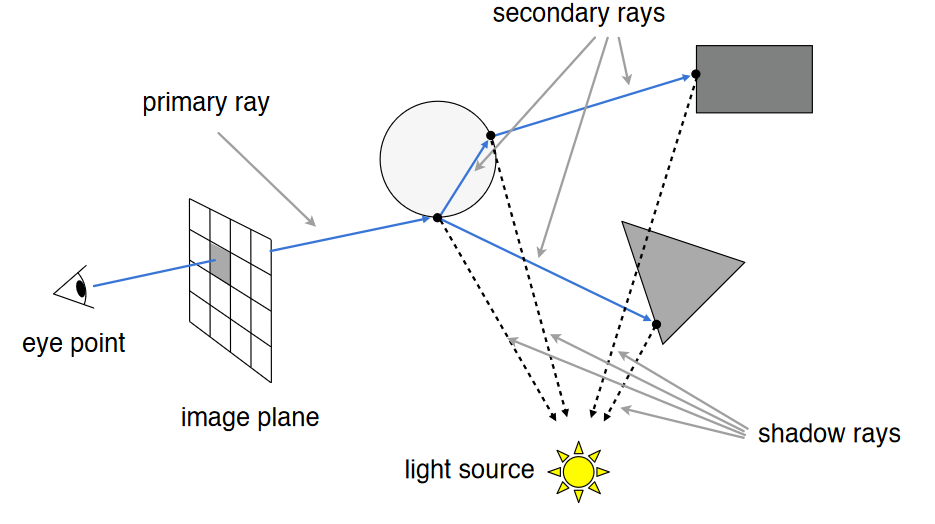
计算光线和物体表面的交点
隐式表面(光线和表达式面)
定义光源:o:光源的位置d:单位方向
定义球:c:球心p:球上任一点
R
a
y
:
r
(
t
)
=
o
⃗
+
t
d
⃗
,
0
≤
t
<
∞
S
p
h
e
r
e
:
p
:
(
p
−
c
)
2
−
R
2
=
0
联
立
方
程
可
得
⟹
(
o
+
t
d
−
c
)
2
−
R
2
=
0
Ray:quad r(t) = vec{o} + tvec{d},quad 0leq t< infty \ Sphere:quad p:(p-c)^2-R^2 = 0 \ 联立方程可得Longrightarrow (o + td - c)^2 - R^2 = 0
Ray:r(t)=o+td,0≤t<∞Sphere:p:(p−c)2−R2=0联立方程可得⟹(o+td−c)2−R2=0
最后结果无非就是求一个两次函数方程,可以将球的方程推广到一般的隐式函数,交点一定即在光线上,又在表面上,思路就是联立二者方程求解
显式表面(光线和三角形)
光和三角形求交点,可看作光先和三角形所在平面求交点,再判断是否在三角形内,而后者在前文已经讨论过了,所以现在要先找到三角形所在平面,定义一个平面这里采用点法式(用法线和不过法线的点定义一个平面)
p
:
(
p
−
p
′
)
⋅
N
=
0
p:(p-p')cdot N = 0
p:(p−p′)⋅N=0
同理,联立光线和平面的方程即可求出参数 t
t
=
(
p
′
−
o
)
⋅
N
d
⋅
N
(
0
≤
t
<
∞
)
t = frac{(p'-o)cdot N}{dcdot N} quad (0leq t < infty)
t=d⋅N(p′−o)⋅N(0≤t<∞)
另一种思路是直接求一个在三角形内的交点,采用之前提过的重心坐标去表示三角形内的一个点,然后解一个线性方程组
o
⃗
+
t
d
⃗
=
(
1
−
b
1
−
b
2
)
P
0
⃗
+
b
1
P
1
⃗
+
b
2
P
2
⃗
vec{o} + tvec{d} = (1- b_1 - b_2)vec{P_0}+b_1vec{P_1}+b_2vec{P_2}
o+td=(1−b1−b2)P0+b1P1+b2P2
加速求光线和表面的交点
原始做法是遍历每个面求光线和该面的最近的交点,计算会很慢。加速的思路是使用 Bounding Volumes,用一个简单的几何体把物体包围起来(其实只要取模型 xyz 的最大小值就可以求出来),先进行一粗操作,判断碰不到 bounding volumes 的光线自然不可能照射到物体
一般来说,用的 Bounding Volumes 是轴对齐包围盒 Axid-Aligned Bounding Box(AABB),该长方体的边与坐标轴都是平行或垂直的。
我们将长方体看作是三对对面的交集形成的几何体,那么先分别求三个对面光线进入的 t_min 和 t_max,然后对于长方体来说,光线进入长方体的时间 t_enter=max{t_min}、离开长方体的时间 t_exit=min{t_max},如果 t_enter<t_exit,那么这段时间内光线就在长方体里,即有交点,反之就没有交点。
但上面是考虑了光线为直线,实际上光线是射线,所以考虑负值的情况
- t_exit<0,说明长方体在光线背后,不可能有交点
- t_exit>=0 & t_enter <0,说明光源的位置在盒子里面,一定有交点
光
线
和
A
A
B
B
有
交
点
⟺
t
e
n
t
e
r
<
t
e
x
i
t
&
t
e
x
i
t
≥
0
光线和AABB有交点 Longleftrightarrow t_{enter}<t_{exit}; &; t_{exit}geq 0
光线和AABB有交点⟺tenter<texit&texit≥0
加速结构 Acceleration
均匀格子 Uniform Grids
在光线追踪之前进行预处理:
- 找到包围盒
- 划分格子
- 在与物体表面相交的格子里存储每个物体
格子不能太稀疏,也不能太密集,常用的格子数为 27*num_of_obj,对于物体分布均匀的场景比较好用
空间划分 Spatial Partitions
对于分布不均匀的场景,在稀疏的地方仍然采用相同大小的格子会造成一定的浪费
空间划分并不是图形学的专属,早在几何上就有了一定的应用,还有一些结构比如八叉树Oct-Tree、KD-Tree、BSP-Tree
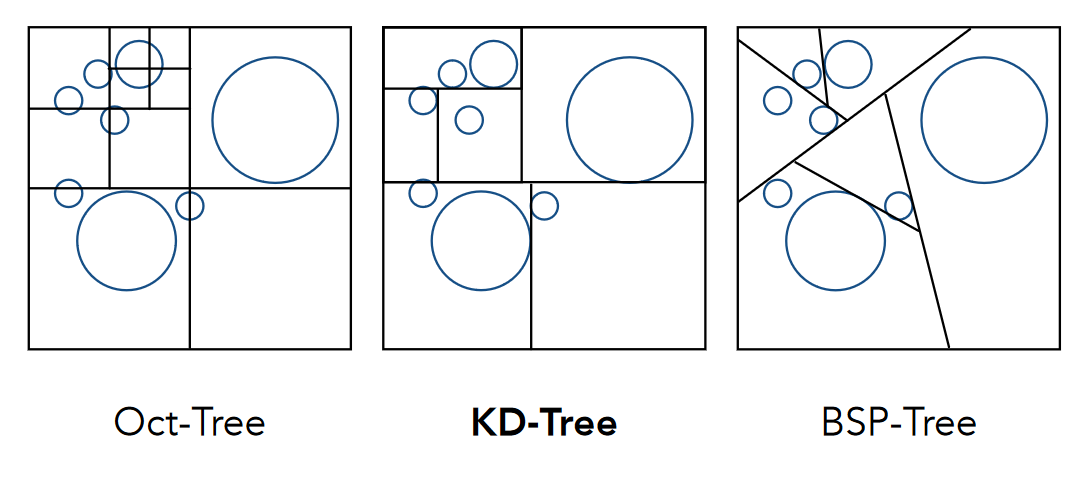
KD-Tree
定义数据结构:
中间节点
- 划分轴 split axis
- 划分的位置 split position
- 子节点 children:指向两个子节点
叶子节点
- 物体的列表 list of objects
遍历 KD-Tree,对于有交点的空间判断与其内部物体是否有交点,没有交点的盒子不再判断(二叉树剪枝)
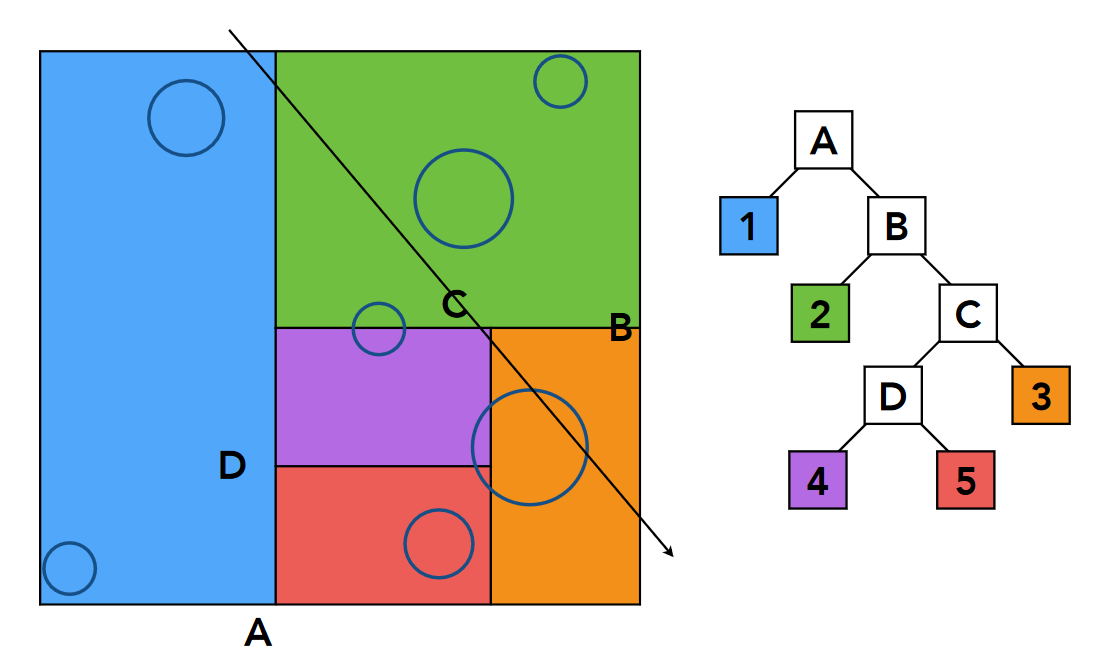
物体划分 Object Partitions
对于空间划分,以KD-Tree为例,它的缺点一个是要表示盒子与三角形包含关系不容易,另一个是一个物体可能由多个叶子节点存储。
Bounding Volume Hierarchy(BVH)
BVH 的思想是并不划分空间,而是划分物体,将一堆物体划分两堆再重新求 Bounding Volume,这样保证了一个物体只可能出现在一个 Bounding Volume 里,且已知物体重新求包围盒也比较简单
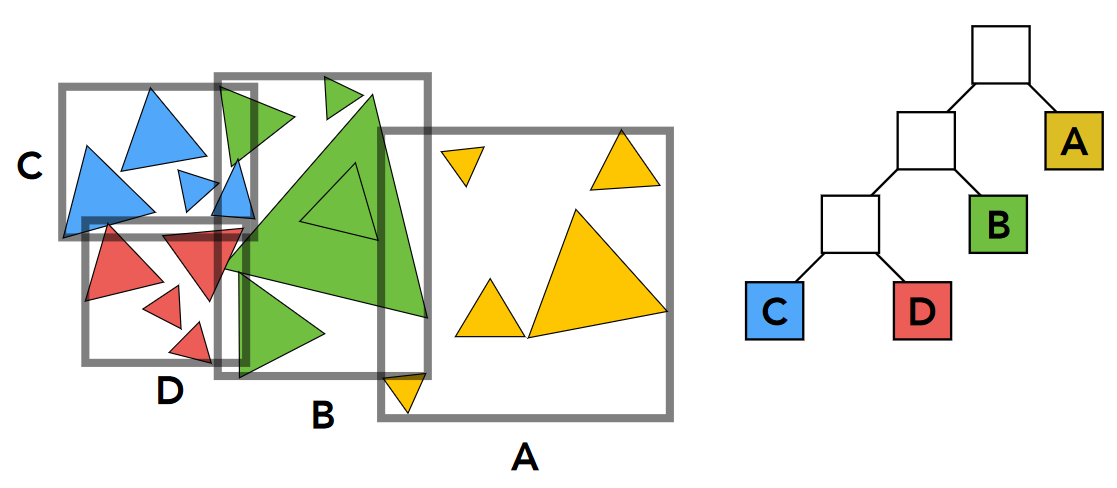
划分的一些规则:
- 总是选择最长的轴向进行划分
- 在中间物体位置处进行划分(保证树平衡,最大深度小)
定义 BVH 的数据结构:
中间节点
- 包围盒 bounding box
- 子节点 children:指向两个子节点
叶子节点
- 包围盒 bounding box
- 物体的列表 list of objects
Nodes represent subset of primitives in scene
- 子树中的所有物体
辐射度量学 Radiometry
- 辐照能量 Radiant Enery
总能量Q,单位:焦耳 J
- 辐照通量 Radiant Flux
单位时间接受的能量,功率,单位:瓦特 W
- 辐照强度 Intensity
从一个源向周围发射光,每单位立体角的能量,单位:W/sr
- 辐[射]照度 Irradiance
物体表面接受到光的能量
- 辐[射]亮度 Radiance
光线传播中的能量
// 一般图形学中不会使用总能量,较多的是使用单位能量即通量叫做能量
辐照强度 Intensity
每单位立体角的能量,单位:W/sr
平面角是弧长/半径,立体角是面积/半径平方
Ω
=
A
r
2
Omega = frac{A}{r^2}
Ω=r2A
微分立体角
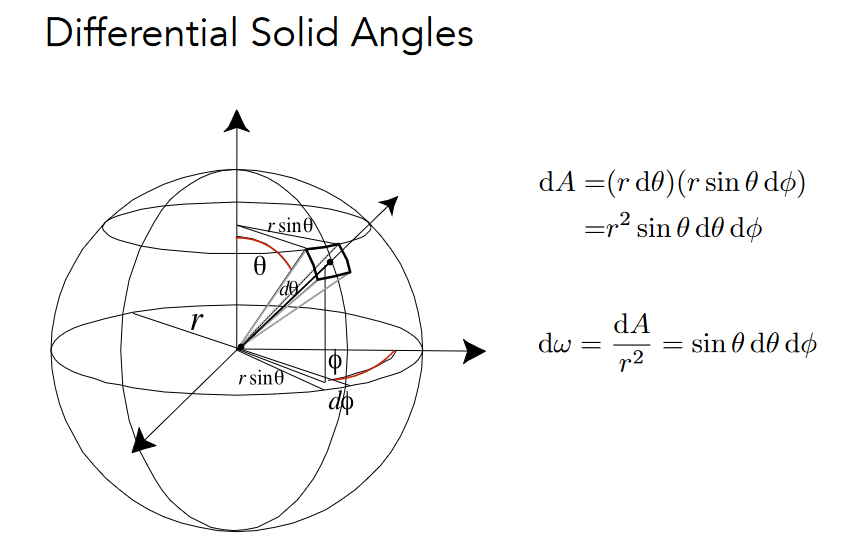
辐[射]照度 Irradiance
单位面积上的辐射通量,单位:W/m²
可以解释之前点光源能量与距离的平方成反比,并不是辐照强度变小了,而是面积变大导致 irradiance 变小
辐[射]亮度 Radiance
每单位立体角和每单位投影面积上,由表面反射、发射或接收的能量。单位:W/sr·m²
L
(
p
,
ω
)
=
d
2
Φ
(
p
,
ω
)
d
ω
⋅
d
A
cos
θ
=
d
I
(
p
,
ω
)
d
A
cos
θ
L(p,omega) = frac{d^2Phi(p,omega)}{domegacdot dAcos θ} = frac{dI(p,omega)}{dAcos θ}
L(p,ω)=dω⋅dAcosθd2Φ(p,ω)=dAcosθdI(p,ω)
// Irradiance 和 Radiance 的区别就是是否有方向性
双向反射分布函数 BRDF
Bidirectional Reflectance Distribution Function
已知入射光能量和角度,射到物体表面后会向各个方向辐射,BRDF就是用来求某个方向到底辐射了多少能量
// 可以理解为入射光就是单位面积单位立体角度的 radiance,该表面接收到所有方向的 radiance 转换为 irradiance,之后反射为各个方向的 radiance
就是一个比例关系,对任一初涉方向的 radiance,除以该单位面积的 irradiance
f
r
(
ω
i
→
ω
r
)
=
d
L
r
(
ω
r
)
d
E
i
(
ω
i
)
=
d
L
r
(
ω
r
)
L
i
(
ω
i
)
cos
θ
i
d
ω
i
f_r(omega_irightarrow omega_r) = frac{dL_r(omega_r)}{dE_i(omega_i)} = frac{dL_r(omega_r)}{L_i(omega_i)cos θ_idomega_i}
fr(ωi→ωr)=dEi(ωi)dLr(ωr)=Li(ωi)cosθidωidLr(ωr)
其中
$θ_i:法线与入射方向的夹角
θ_r:法线与出射方向的夹角
L_i(x,omega_i):入射光
L_r(x,omega_r):出射光$
BRDF描述了光与物体如何作用,决定了物体不同的材质
反射方程
L
r
(
p
,
ω
r
)
=
∫
H
2
f
r
(
p
,
ω
i
→
ω
r
)
L
i
(
p
,
ω
i
)
cos
θ
i
d
ω
i
L_r(p,omega_r) = int_{H^2}f_r(p,omega_irightarrowomega_r)L_i(p,omega_i)cos{θ_i}domega_i
Lr(p,ωr)=∫H2fr(p,ωi→ωr)Li(p,ωi)cosθidωi
从反射方程中可以看到,任何出射的 radiance 都可以作为一个入射的 radiance 。光线的多次弹射,会让方程不断地递归
渲染方程
L
o
(
p
,
ω
o
)
=
L
e
(
p
,
ω
o
)
+
∫
Ω
+
L
i
(
p
,
ω
i
)
f
r
(
p
,
ω
i
,
ω
o
)
(
n
⋅
ω
i
)
d
ω
i
L_o(p,omega_o) = L_e(p,omega_o) + int_{Omega +}L_i(p,omega_i)f_r(p,omega_i,omega_o)(ncdot omega_i)domega_i
Lo(p,ωo)=Le(p,ωo)+∫Ω+Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi)dωi
渲染方程可以看作是物体的自发光加上反射光组成,可以用算子简写为
L
=
E
+
K
L
L=E+KL
L=E+KL
可解出
L
=
E
+
K
E
+
K
2
E
+
K
3
E
+
⋯
+
K
n
E
L=E+KE+K^2E+K^3E+dots + K^nE
L=E+KE+K2E+K3E+⋯+KnE
其中 E 表示不弹射,KE 表示一次反射,之后的项分别表示二次、三次、多次反射。这个算子式可理解为光线对弹射次数的分解
全局光照
所有的弹射次数光线相加就是全局关照
光栅化的着色只有 K+KE ,也就是最多到一次反射,对于二次弹射以上的间接光照,光栅化很难做
路径追踪就是一种解全局光照/渲染方程的方式
蒙特卡洛积分与路径追踪
蒙特卡洛积分 Monte Carlo Integration
为了解决一个定积分问题,定积分的数值大小就是该函数与积分上下限和 x 轴围成图形的面积,蒙特卡洛的思想就是通过随机多次采样求平均近似的计算这个面积
F
N
=
1
N
∑
i
=
1
N
f
(
X
i
)
p
(
X
i
)
F_N = frac{1}{N}sum_{i=1}^N frac{f(X_i)}{p(X_i)}
FN=N1∑i=1Np(Xi)f(Xi)
蒙特卡洛积分
∫
f
(
x
)
d
x
=
1
N
∑
i
=
1
N
f
(
X
i
)
p
(
X
i
)
X
i
∼
p
(
x
)
int f(x)dx = frac{1}{N}sum_{i=1}^Nfrac{f(X_i)}{p(X_i)} quad X_isim p(x)
∫f(x)dx=N1∑i=1Np(Xi)f(Xi)Xi∼p(x)
路径追踪 Path Tracing
Whitted-Style ray tracing:
- 光线到达光滑表面进行反射或折射
- 在漫反射表面停止反射
第一个问题是对于 Glossy 材质并不能简单的沿着镜面方向反射,第二个问题是漫反射仍然会有反射,光线打到 Diffuse 面上不应该简单的就停止了。
Path Tracing 就是为了解决 Whitted-Style ray tracing 的这些问题,但是渲染方程仍然是按照逻辑推理出的正确方程
从形式上来看,渲染方程要求的是一个积分值,可以采用蒙特卡洛积分方法,对不同的方向采样
先只考虑直接光照
f
(
x
)
=
L
i
(
p
,
ω
i
)
f
r
(
p
,
ω
i
,
ω
o
)
(
n
⋅
ω
i
)
d
ω
i
p
d
f
(
x
)
=
1
2
π
f(x)= L_i(p,omega_i)f_r(p,omega_i,omega_o)(ncdot omega_i)domega_i\ pdf(x) = frac{1}{2pi}
f(x)=Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi)dωipdf(x)=2π1
所以得到
L
(
p
,
ω
o
)
≈
1
N
∑
i
=
1
N
L
i
(
p
,
ω
i
)
f
r
(
p
,
ω
i
,
ω
o
)
(
n
⋅
ω
i
)
p
d
f
(
ω
i
)
L(p,omega_o) approx frac{1}{N}sum_{i=1}^N frac{L_i(p,omega_i)fr(p,omega_i,omega_o)(ncdot omega_i)}{pdf(omega_i)}
L(p,ωo)≈N1∑i=1Npdf(ωi)Li(p,ωi)fr(p,ωi,ωo)(n⋅ωi)
伪代码:
shade(p, wo)
{
Randomly choose N directions wi~pdf;
float Lo = 0.0;
For each wi
{
Trace a ray r(p, wi)
If ray r hit the light
Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
}
Return Lo
}
继续考虑间接光照,当光线打到另一物体时,意味着会有反射光线,可以把这个物体也当作一个光源看待
shade(p, wo)
{
Randomly choose N directions wi~pdf;
float Lo = 0.0;
For each wi
{
Trace a ray r(p, wi);
if(ray r hit the light)
Lo += (1 / N) * L_i * f_r * cosine / pdf(wi);
else if(ray r hit an object at q)
Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi);
}
Return Lo
}
但是这样会带来指数爆炸的问题。蒙特卡洛方法中,若取 N=1 时,即并不是随机取光线方向,而是只取某一个方向,不会导致指数爆炸问题,这种方法就是路径追踪
俄罗斯轮盘赌 Russian Roulette
另一个问题是算法是递归的,但是递归有两个条件,其中之一是要有终止的条件,但是算法中没有会造成无限递归。为了解决这个问题,引入俄罗斯轮盘赌的思想,以一定概率 p 发射光线,得到的值除以概率 p,那么还有 1-p 的概率不发射光线,最后得到的期望就是要求的值
E
=
P
×
(
L
o
P
)
+
(
1
−
p
)
×
0
=
L
o
E = Ptimes(frac{L_o}{P}) + (1-p)times 0 = L_o
E=P×(PLo)+(1−p)×0=Lo
shade(p, wo)
{
Manually specify a probability P_RR;
Randomly select ksi in a uniform dist. in [0, 1];
if(ksi > P_RR)
return 0.0;
Randomly choose ONE direction wi~pdf(w)
Trace a ray r(p, wi)
if(ray r hit the light)
return L_i * f_r * cosine / pdf(wi) / P_RR
Else if(ray r hit an object at q)
return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR
}
由于光线是以一定概率打出的,所有采样的方式,即 p(x) 会有一定的影响,均匀采样可能会造成“打出无用光线”的浪费,为了不浪费,想让光线在光源面积上采样,但是积分是在立体角上,不能使用蒙特卡洛积分,要将渲染方程改写成在光源面积上的积分
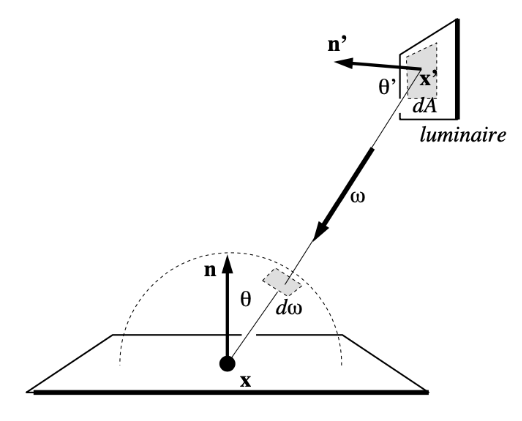
先找到 dω 和 dA 的关系
d
ω
=
d
A
cos
θ
′
∥
x
′
−
x
∥
2
domega = frac{dAcos θ'}{left | x'- x right |^2}
dω=∥x′−x∥2dAcosθ′
重写渲染方程对光源面积积分 dA
L
o
(
x
,
ω
o
)
=
∫
A
L
i
(
x
,
ω
i
)
f
r
(
x
,
ω
i
,
ω
o
)
cos
θ
cos
θ
′
∥
x
′
−
x
∥
2
d
A
L_o(x,omega_o) = int_{A}L_i(x,omega_i)f_r(x,omega_i,omega_o)frac{cos θcos θ'}{left | x'- x right |^2} dA
Lo(x,ωo)=∫ALi(x,ωi)fr(x,ωi,ωo)∥x′−x∥2cosθcosθ′dA
现在着色就可以分为两部分:
- 来自光源,直接光线,不需要 RR
- 其它物体反射,间接光线,需要 RR
shade(p, wo)
{
# Contribution from the light source.
Uniformly sample the light at x’ (pdf_light = 1 / A);
Shoot a ray from p to x';
if(the ray is not blocked in the middle) // 直接光照不被遮挡
L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light;
# Contribution from other reflectors.
float L_indir = 0.0;
Test Russian Roulette with probability P_RR;
Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi);
Trace a ray r(p, wi);
if(ray r hit a non-emitting object at q)
L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR;
Return L_dir + L_indir;
}
材质与外观 Materials and Appearances
不同的材质对应不同的外观,在图形学中 BRDF 是决定 Materials 的一项
漫反射系数 albedo
假设入射光都是均匀的,物体不吸收光,那么由于能量守恒,反射光也是已知均匀的。假设 入射的 radiance 和 BRDF 都为常数,就是对半球 cosθ 的积分
KaTeX parse error: No such environment: align at position 7: begin{̲a̲l̲i̲g̲n̲}̲ L_o(omega_o) …
在上述假设的情况下,由于能量守恒 BRDF = 1/pai,定义 [0, 1] 的反射率 albedo 为 ρ
f
r
=
ρ
π
f_r = frac{rho}{pi}
fr=πρ
Caustics 焦散其实本质是海水的聚焦
折射定律 Snell’s Law
折射率为 η
η
i
sin
θ
i
=
η
i
sin
θ
t
eta_i sintheta_i = eta_i sintheta_t
ηisinθi=ηisinθt
当从光疏到光密介质,可能发生全反射
折射满足 BTDF ,而反射 BRDF + 折射 BTDF = 散射 BSDF
菲涅尔项 Fresnel Reflection / Term
反射与入射光的方向是有关的
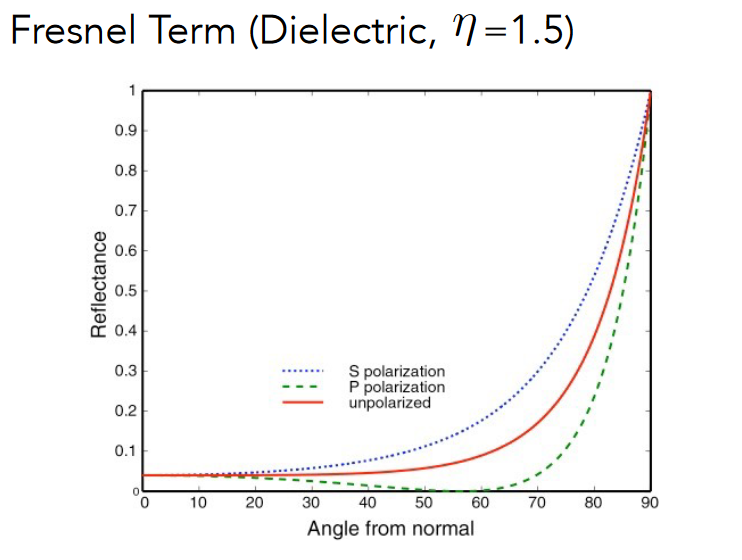
红线表示绝缘体菲涅尔项,如果入射光与表面几乎平行,那么几乎全部反射,如果垂直几乎全部折射,反射光不到 5%
另外两条线是光线的极化性质,只沿着某一方向振动,就是偏振光
但是对于金属来说,菲涅尔项是不一样的
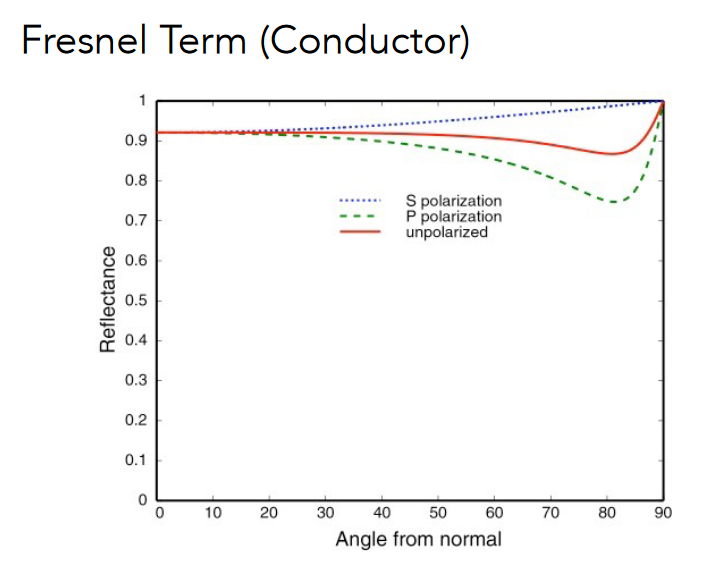
用曲线近似拟合,可以得到对导体和绝缘体的通式
R
(
θ
)
=
R
0
+
(
1
−
R
0
)
(
1
−
cos
θ
)
5
R
0
=
(
n
1
−
n
2
n
1
+
n
2
)
2
R(theta) = R_0 + (1-R_0)(1-costheta)^5\ R_0 = (frac{n_1-n_2}{n_1+n_2})^2
R(θ)=R0+(1−R0)(1−cosθ)5R0=(n1+n2n1−n2)2
微表面材质 Microfacet Material
当离物体足够远,物体的表面是看不见的,看到的是总体的一个效应
微表面理论是说从远处看到的是 Macroscale(Flat & Rough),从近处看到的是 Microscale(Bumpy & Specular),也就是说可以把微表面理解为一个很小的镜面
一个材质的粗糙程度可以用微表面模型的法线分布来表示,越集中越光滑
f
(
i
,
o
)
=
F
(
i
,
h
)
G
(
i
,
o
,
h
)
D
(
h
)
4
(
n
,
i
)
(
n
,
o
)
f(i,o) = frac{F(i,h)G(i,o,h)D(h)}{4(n,i)(n,o)}
f(i,o)=4(n,i)(n,o)F(i,h)G(i,o,h)D(h)
其中 F(i, h) 是考虑菲涅尔项,D(h) 是考虑法线分布,G(i, o, h) 是几何项,表示微表面之间的互相遮挡作用
基本上 PBR 都会使用微表面模型
各向同/异性材质 Isotropic / Anisotropic Materials
例子:电梯里的高光并不是一个圆形,而是一条一条的线。因为材质是磨过的金属,会体现各向异性
所谓各向同性,是指微表面的材质并不存在方向性
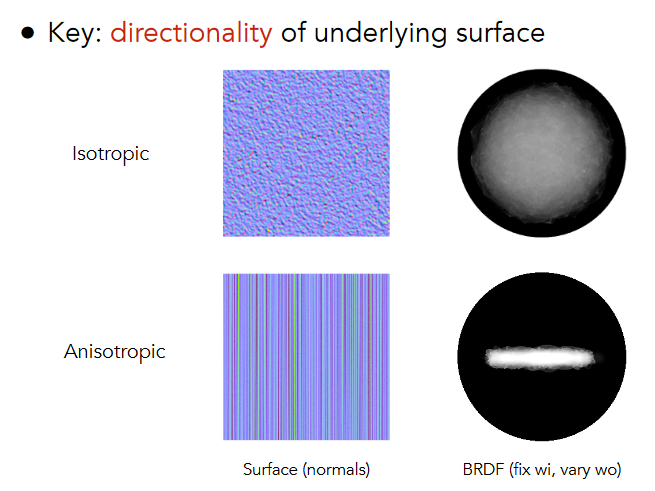
BRDF 的性质
- 非负性
- 线性性质
- 可逆性
- 能量守恒
- 对于各向同性的 BRDF 只与方位角的插值有关,可看作降低一维;对于各向异性 BRDF 方位角不需要考虑正负
BRDF 的测量
固定观测点,让相机和光源以球形环绕,可以得到所有的输入对,从而进行测量,但是数据是四维的,如果是各向同性可以降低一维,如果是各向异性可以只考虑一半
高级光线传播 Advanced Light Transport
蒙特卡洛的估计方法,如果期望值等于真实值则是无偏的,否则是有偏的。对于有偏估计,样本足够多的情况下会收敛于真实值,称为一致的
无偏光线传播方法
双向路径追踪 Bidirectional Path tPTracing(BDPT)
从光源和摄像机双向追踪,各找到半路径,再将半路径的端点连起来就是全路径
// 当光源第一次直接照射集中在某个区域的时候,比较适用
Metropolis Light Transport(MLT)
使用马尔科夫链蒙特卡洛 Markov Chain Monte Carol(MCMC),即已知一个样本,根据这个样本生成下一个样本。用这个工具可以生成一系列以任意函数形状作为 PDF 的样本
// Metropolis 不是大都市,是人名
对于某些复杂场景效果比较好,因为只要找到一条路径作为种子,就可以找到周围的路径,但是缺点是无法确定收敛时间,且是局部的行为,可能导致画面比较脏
有偏光线传播方法
光子映射 Photon Mapping
先从光源向各个方向发射光子直到打到 Diffuse 物体上,然后从摄像机出发也发射光线直到打到 Diffuse 物体上。计算局部光子密度,分布越集中的地方越亮
Vertex Connection and Merging(VCM)
一种结合光子映射和双向路劲追踪,如果两个端点很近,就不连接了,当作光子来计算
实时辐射度算法 Instant Radiosity(IR)
并不区分光线是自己发出的还是反射来的,已经被照亮的地方都认为是光源再照亮别的地方
高级外观建模 Advanced Appearance Modeling
非表面模型 Non-surface Models
散射/参与介质 Participating Meida
云层这种空间中的物质,光线在传播过程中会被吸收和散射,由相位函数 Phase Function 来定义如何散射。
有些表面光线是能够穿透进去,比如巧克力。
头发/毛发/纤维 Hair / Fur / Fiber(BCSDF)
考虑光线和曲面的作用,有两种高光,无色高光和有色高光。
头发
广泛应用的一种模型叫做 Marchner Model,把头发当作圆柱体
- 外皮 Cortex
- 角质层 Cuticle
考虑三种光线的作用:
- 反射 R
- 折射+折射 TT
- 折射+反射+折射 TRT
毛发
人的头发和动物毛发有着结构上的差异,动物毛发里的髓质更大,光线进去了更容易发生反射,所以上述方法并不适用
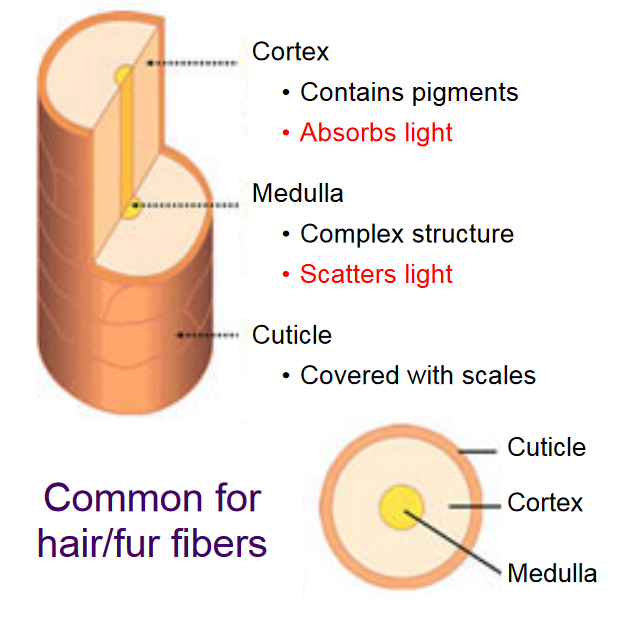
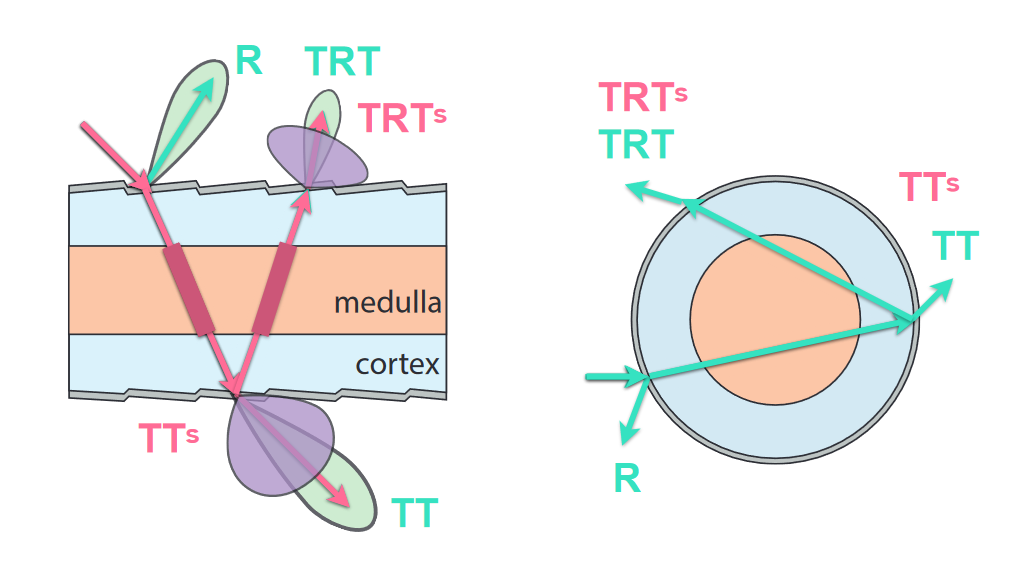
双层圆柱模型 Double Cylinder Model,考虑光线的五种作用:
- R
- TT
- TRT
- 散射后的折射+折射 TTS
- 散射后的折射+反射+折射 TRTS
颗粒 Granular Material
可以认为许多颗粒按一定百分比组成一个较大的体积
表面模型 Surface Models
半透明 Translucent Material(BSSRDF)
光线从一个方向进来,散射后从另一些方向出去,透明并不是指光线直线传播
E.g. 牛奶、人的皮肤、玉石
次表面散射 BSSRDF
次表面散射可理解为 BRDF 的衍生
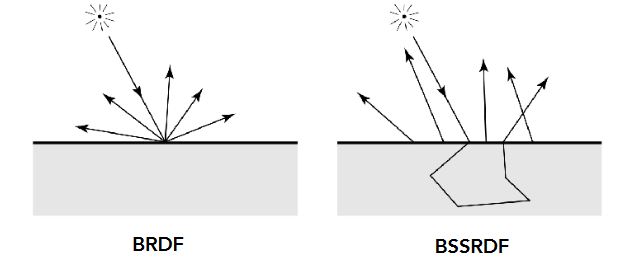
L
(
x
o
,
ω
o
)
=
∫
A
∫
H
2
S
(
x
i
,
ω
i
,
x
o
,
ω
o
)
L
i
(
x
i
,
ω
i
)
cos
θ
d
ω
i
d
A
L(x_o,omega_o) = int_Aint_{H^2}S(x_i,omega_i,x_o,omega_o)L_i(x_i,omega_i)cos theta domega_i dA
L(xo,ωo)=∫A∫H2S(xi,ωi,xo,ωo)Li(xi,ωi)cosθdωidA
布料 Cloth
一系列缠绕的纤维,有两种缠绕的等级
第一次缠绕形成一股 Ply,很多股再缠绕形成线 Yarn
三个思路:
- 认为织物是在空间中分布的体积,划分成多个很细小的格子,性质转换成云烟雾的渲染
- 一根一根纤维渲染
- 当成物体表面渲染
Detailed Material(non-statistical BRDF)
太真实的反而不真实,现实中会有一定瑕疵和划痕,可以用前文提过的微表面模型
程序化生成模型 Procedural Appearance
并不生成纹理,而是需要的时候通过函数查询,即给定空间中的 x, y, z 就会返回一个值。比如 noise 函数。
常应用在地形上
相机与透镜 Cameras and Lenses
成像 Imaging = 合成 Synthesis + 捕捉 Capture
视场 Filed of View
传感器的宽度 h,传感器到镜头的距离 Focallength:f
F
O
V
=
2
arctan
(
h
2
f
)
FOV = 2 arctan{(frac{h}{2f})}
FOV=2arctan(2fh)
通常用默认 35mm 格式的传感器 Sensor,以焦距来定义 FOV 的大小
例如在标准情况下:
- 17mm 是广角镜头 104°
- 50mm 是正常镜头 47°
- 200mm 是长焦镜头 12°
// 手机所谓的 28mm 焦距指的是“等效”焦距,即在 35mm 格式传感器下的焦距
曝光 Exposure
曝光度(H)= 时间(T) × Irradiance(E)
影响曝光度的因素
- 光圈大小 Aperture Size:通过 f-stop 控制光圈大小
- 快门速度 Shutter Speed:快门开放的时间
- 感光度 ISO gain:可以理解为一种后期处理,接收到多少光后再乘以一个数
镜头 Lens
实际上相机使用的是一组复杂的透镜组,通过不同的组合可以实现调整焦距的效果
Defocus Blur
由于 物距分之一加像距分之一等于焦距分之一 这个关系,当物体不在 Focal Plane 时,成像点也就不在感光面上,原来的一个点就变成了一个圆,即 Circle of Confusion(CoC)
景深 Depth of Field
光圈的大小会影响模糊的范围,光圈越小景深越大
景深就是指成像清晰的一段范围
光场、颜色与感知 Light Field, Color and Perception
全光函数 The Plenoptic Function
三维世界的场景转换到幕布上显示对人眼来说是等价的,虚拟现实就是这个原理
可以用全光函数来描述上述过程
P
(
θ
,
ϕ
)
P(theta,phi)
P(θ,ϕ)
引入波长后可以表示颜色
P
(
θ
,
ϕ
,
λ
)
P(theta,phi, lambda)
P(θ,ϕ,λ)
扩展时间 t 后表示电影,如果再加入观察点的位置坐标,就是一个全息电影
P
(
θ
,
ϕ
,
λ
,
t
,
V
X
,
V
Y
,
V
Z
)
P(theta,phi, lambda, t, V_X, V_Y,V_Z)
P(θ,ϕ,λ,t,VX,VY,VZ)
将这个函数看作在任何时间任何位置向任何方向看,看到整个世界的颜色。那么整个世界就可以被定义成一个七维的函数,即全光函数
光场 Light Field
在任何一个位置,向任何一个方向去的光的强度。二维的位置可以用 (u, v) 表示,二维的方向可以用 (θ, φ) 表示。
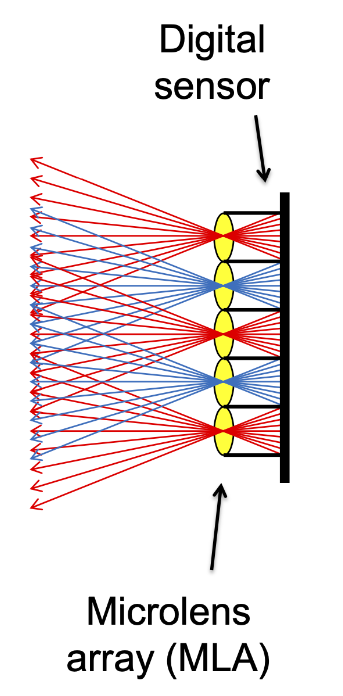
光场摄像机 Light Field Camera
利用微透镜原理,将来自一个像素的光通过不同的透镜分开记录,从而可以支持后期的重新聚焦
颜色与感知 Color and Perception
颜色的物理基础 Physical Basis of Color
光谱 Spectrum of Light
光不同的波长对应不同的折射率,可视光的波长范围为 400nm~700nm
谱功率密度 Spectral Power Distribution(SPD)
SPD 描述了一个光在各个波长的能量分布
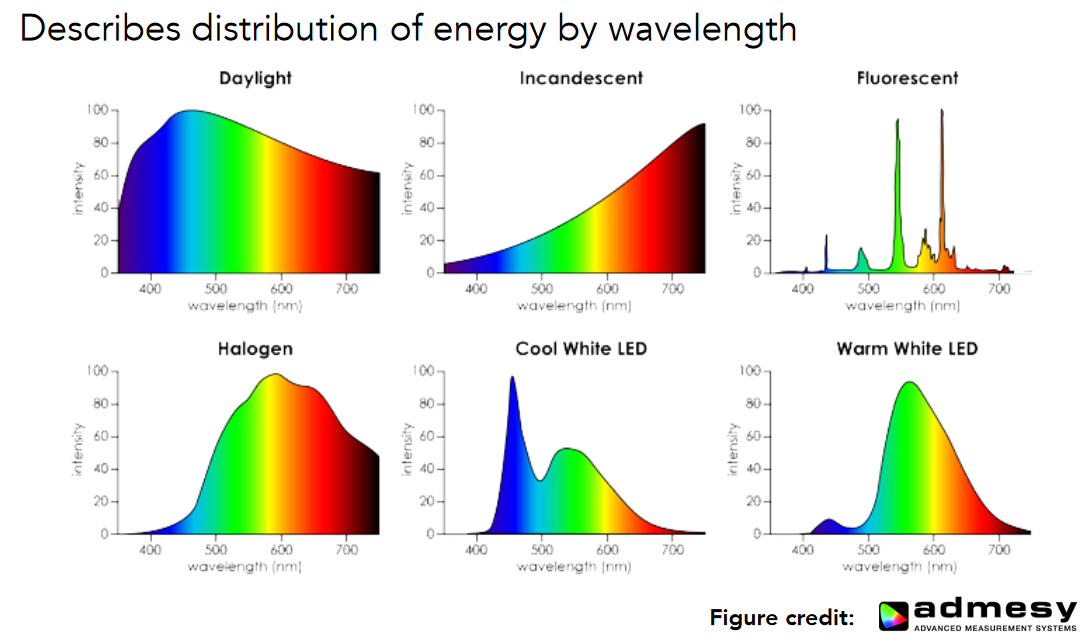
三色理论 Tristimulus Theory of Color
颜色是一种人类感知的现象,跟实际的光的分布并没有关系。
在人眼的视网膜上有感光细胞,包括
- 棒状细胞 Rod Cells:感知光的强度(灰度图)
- 锥形细胞 Cone Cells:感知光的颜色
- S-Cone
- M-Cone
- L-Cone
锥形细胞 Cone Cells 又分为三类 S, M, L 感知不同波长光的强度
$S = int r_S(lambda)spd(lambda)dlambda
M = int r_M(lambda)spd(lambda)dlambda
L = int r_L(lambda)spd(lambda)dlambda $
所以眼睛看到了并不是“光谱”,而是“三个数 S, M, L”
同色异谱 Metamerism
由于 SML 是积分得到的结果,所以完全可能存在不同的波长得出相同的 SML 结果。可以利用这点调节波长,使得颜色看上去相同
颜色复制和匹配 Color Reproduction / Matching
计算机中使用的是“加色系统”,即 RGB 都是 255 的时候呈现白色
// 现实中画画是“减色系统”,混合各种颜色得到黑色
加色系统允许使用三种颜色混合相加得到相同的颜色
颜色空间 Color Space
标准 Standardized RGB(sRGB)
广泛应用的一种颜色空间,但是色域是有限的
通用颜色系统 CIE XYZ
生活中不怎么常用,在科学领域用的比较多
HSV Color Space
- 色调 Hue
- 饱和度 Saturation
- 亮度 Lightness(Value)
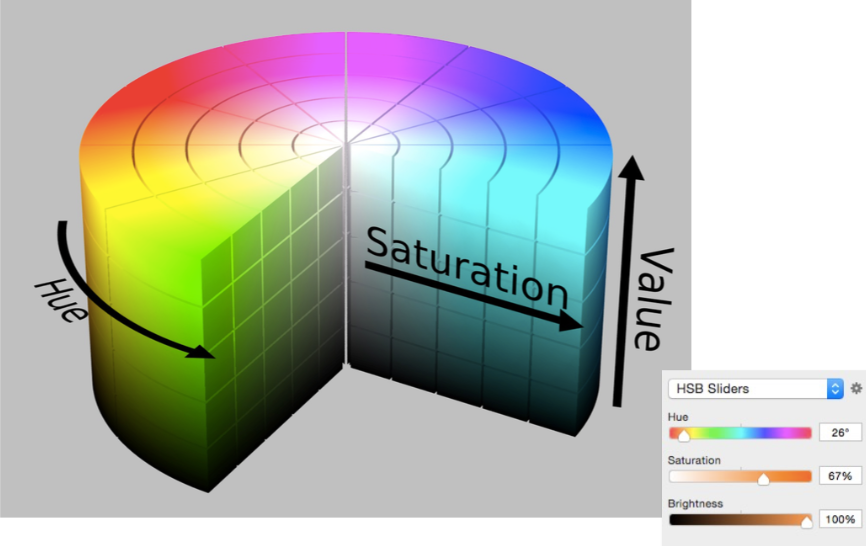
CMYK:Subtractive Color Space
CMYK 是一个减色系统,对应 Cyan, Magenta, Yellow, Key
混合 CMY 可以得到 K,但是这种系统多应用于印刷,为了节约成本所以带了一个 K
动画与模拟 Animation / Simulation
动画可看作三维空间在时间上的一个扩展
First hand-drawn feature-length animation is “Snow White and the Seven Dwarfs” (1937)
第一部手绘的剧场版动画是 1937 年的白雪公主
First CG (computer-generated) feature-length animation is “Toy Stoty” (1995)
第一部电脑生成的剧场版动画是 1995 年的玩具总动员
关键帧动画 Keyframe Animation
关键帧插值控制可以用贝塞尔曲线
物理模拟 Physical Simulation
利用牛顿力学 F=ma 等计算作用力、速度,从而得出位置的思想
- 布料
- 流体
- 头发
质点弹簧系统 Mass Spring Rope
一些列相互连接的质点和弹簧,最基本的单元是两个质点加中间一个弹簧
f
a
→
b
=
k
s
(
b
⃗
−
a
⃗
)
∥
b
−
a
∥
(
∥
b
−
a
∥
−
l
)
f
b
→
a
=
−
f
a
→
b
f_{arightarrow b} = k_sfrac{(vec{b}-vec{a})}{left|b-aright|}(left|b-aright|-l) \ f_{brightarrow a} = -f_{arightarrow b}
fa→b=ks∥b−a∥(b−a)(∥b−a∥−l)fb→a=−fa→b
弹簧满足胡克定律,但是这个理想模型由于动量守恒会永远运动下去,所以需要加一个摩擦力 Damping Force
f
=
−
k
d
b
˙
f = -k_ddot{b}
f=−kdb˙
其中 dot{b} 表示 b 位置的导数,即 b 的速度,但是不能只是单纯加上这种力,否则只能表示外部的摩擦作用,不能表示弹簧内部的损耗。内部的摩擦力还应考虑与相对位置有关
f
b
=
−
k
d
(
b
⃗
−
a
⃗
)
∥
b
−
a
∥
⋅
(
b
˙
−
a
˙
)
⋅
b
⃗
−
a
⃗
∥
b
−
a
∥
f_b = -k_dfrac{(vec{b}-vec{a})}{left|b-aright|}cdot(dot{b} - dot{a})cdot{frac{vec{b}-vec{a}}{left|b-aright|} }
fb=−kd∥b−a∥(b−a)⋅(b˙−a˙)⋅∥b−a∥b−a
// 需要的是沿 ab 方向投影后的相对速度
粒子系统 Particle Systems
- 吸引和排斥力 Attraction and Repulsion Forces
- 重力 Gravity
- 电磁力 Electromagnetism
- 弹簧力 Springs
- 推进力 Propulsion
- 阻尼力 Damping Forces
- 摩擦力 Friction
- 空气阻力 Air Drag
- 粘滞力 Viscosity
- 碰撞 Collisions
- Walls, containers, fixed objects, …
- Dynamic objects, character body parts, …
运动学 Kinematics
前向运动学 Forward Kinematics
关节类型
- Pin(1D rotation) // 图钉
- Ball(2D rotation) // 关节球
- Prismatic joint(translation) // 例如小腿被拉长
优点是直接控制很方便,缺点是要实现和物理一致的效果很费时费力
逆向运动学 Inverse Kinematics
已知点子节点求父节点,存在的问题是 IK 的解并不唯一或者无解
绑定 Rigging
通过添加控制点,使得操控模型更加的方便
动作捕捉 Motion Capture
动捕的优点是效率高而且真实,缺点是操作复杂捕捉出的数据可能还需要整理和调整
欧拉方法
欧拉方法 Euler’s Method
假设一个问题,把单个粒子放在某个速度场内,需要求粒子某时刻的位置
欧拉方法的思路是把时间分层小段 △t ,利用上一时刻的位置和速度计算下一时刻的位置和速度
x
t
+
Δ
t
=
x
t
+
Δ
t
x
˙
t
x
˙
t
+
Δ
t
=
x
˙
t
+
Δ
t
x
¨
t
x^{t+Delta t} = x^t + Delta tdot{x}^t \ dot{x}^{t+Delta t} = dot{x}^t + Delta tddot{x}^t
xt+Δt=xt+Δtx˙tx˙t+Δt=x˙t+Δtx¨t
但是欧拉方法的缺点是有误差和不稳定
误差:误差步长 △t 有关,越大的步长偏离实际越多
不稳定:不稳定的地方会随着时间增加而增加(正反馈)
解决欧拉方法不稳定的方法
- Midpoint method / Modified Euler
- Adaptive step size
- Implicit methods
- Position-based / Verlet integration
中点法 Midpoint Method
思想是已知原始点的位置和方向,用欧拉方法模拟下一个点,但是并不使用,而是计算它们的中点的速度,将此速度应用到原始点重新计算欧拉方法,得到最后的“下一个点”
x
m
i
d
=
x
(
t
)
+
Δ
t
2
⋅
v
(
x
(
t
)
,
t
)
x
(
t
+
Δ
t
)
=
x
(
t
)
+
Δ
t
⋅
v
(
x
m
i
d
,
t
)
x_{mid} = x(t) + frac{Delta t}{2}cdot v(x(t),t) \ x(t+Delta t) = x(t) + Delta t cdot v(x_{mid},t)
xmid=x(t)+2Δt⋅v(x(t),t)x(t+Δt)=x(t)+Δt⋅v(xmid,t)
// 也就是用两次欧拉方法,第一次是为了得到中点的速度,第二次才是计算下一个点的位置
自适应步长大小 Adaptive Step Size
对于 △t 步长求出的下一个点的位置,如果和两次 △t/2 步长求出的点的位置差距过大,则认为误差过大,应该采用 △t/2 步长进行两次欧拉方法
// 是否要把 △t 划分成 △t/2 ,取决于两个方法得到的点距离的差距
隐式方法 Implicit Method
用下一个点的状态的位置和速度来计算上一个点的状态
x
t
+
Δ
t
=
x
t
+
Δ
t
x
˙
t
+
Δ
t
x
˙
t
+
Δ
t
=
x
˙
t
+
Δ
t
x
¨
t
+
Δ
t
x^{t+Delta t} = x^t + Delta tdot{x}^{t+Delta t} \ dot{x}^{t+Delta t} = dot{x}^t + Delta tddot{x}^{t+Delta t}
xt+Δt=xt+Δtx˙t+Δtx˙t+Δt=x˙t+Δtx¨t+Δt
// 就是求一个方程组,可以用求根公式,零点方法等求解。计算量比正向欧拉更大,但是反向欧拉更稳定一点
龙格库塔方法 Runge-Kutta Families
Runge-Kutta 是一类方法,其中用的最广泛的是 RK4
x
n
+
1
=
x
n
+
1
6
Δ
t
(
k
1
+
k
2
+
k
3
+
k
4
)
k
1
=
x
˙
k
2
=
d
(
x
+
Δ
t
k
1
2
)
d
(
t
+
Δ
t
2
)
k
3
=
d
(
x
+
Δ
t
k
2
2
)
d
(
t
+
Δ
t
2
)
k
4
=
d
(
x
+
Δ
t
k
3
)
d
(
t
+
Δ
t
)
x_{n+1} = x_n + frac{1}{6}Delta{t}(k_1+k_2+k_3+k_4)\ k_1 = dot{x} \ k_2 = frac{d(x+Delta{t}frac{k_1}{2})}{d(t+frac{Delta{t}}{2})} \ k_3 = frac{d(x+Delta{t}frac{k_2}{2})}{d(t+frac{Delta{t}}{2})} \ k_4 = frac{d(x+Delta{t}k_3)}{d(t+Delta{t})}
xn+1=xn+61Δt(k1+k2+k3+k4)k1=x˙k2=d(t+2Δt)d(x+Δt2k1)k3=d(t+2Δt)d(x+Δt2k2)k4=d(t+Δt)d(x+Δtk3)
龙格库塔是一个4阶的方法,比上面的方法误差更小
// 所谓阶数就是,当 △t 变为 △t/2 时,误差会变为 1/2 的阶数次方
基于位置的方法 Positon-Based / Verlet Integration
思想时通过调整某些位置,使其能够满足图形中的一些特定性质。非物理方法,不保证能量守恒。不稳定,但是简单且实现时间快
刚体模拟 Rigid Body
模拟刚体要求内部所有的点相同的运动,可以看作一个整体的粒子,但是刚体模拟更关心的是一些数据,位置、速度、角度、角速度等
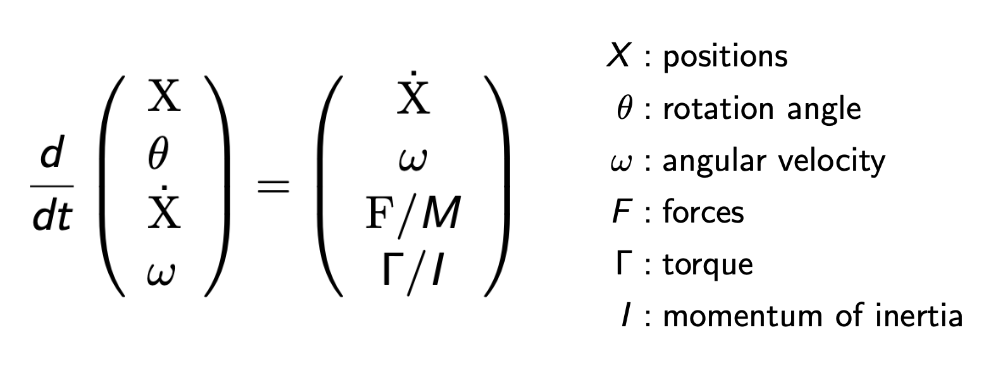
流体模拟 Fluid Simulation
模拟与渲染分离,这里只考虑模拟,基本思想是
- 假设水是由小的刚体球组成、且不能被压缩
- 密度的变化通过改变粒子的位置来实现(梯度下降)
解决流体问题的不同思路:
- 拉格朗日法(质点法)
- 欧拉法(网格法)
- 物质点方法(MPM):综合质点和网格法
最后
以上就是任性镜子最近收集整理的关于图形学基础笔记图形学基础笔记图形学概述向量与线性代数变换 Transformation光栅化 Rasterization着色 Shading拓展:在 unity/UE4 中,开启各向异性过滤,纹理内存并不是 3 倍而是 1/3 。几何 Geometry阴影 Shadows光照追踪 Ray Tracing材质与外观 Materials and Appearances高级光线传播 Advanced Light Transport高级外观建模 Advanced Appearance Modeling相的全部内容,更多相关图形学基础笔记图形学基础笔记图形学概述向量与线性代数变换内容请搜索靠谱客的其他文章。








发表评论 取消回复