电子技术——基本MOS放大器配置

上一节我们探究了一种MOS管的放大器实现,其实MOS放大器还有许多变种配置,在本节我们学习最基本的三大MOS放大器配置,分别是共栅极(CG)、共漏极(CD)、共源极(CS)。
通过上一节我们知道,MOS放大器模型DC分析和小信号分析可以分离,因此在本节我们忽略电路中的DC分析,只关心小信号分析。如何进行DC偏置配置将在下一节学习。
其次,本节我们学习的基本MOS放大器配置都是基于离散模拟电路实现,基于集成模拟电路的MOS放大器配置将在下一章学习。
三大基本配置
MOS管是一个三端器件,而放大器是一个二端器件,因此需要将MOS管的一端共地才能实现二端器件放大器电路,共地的那一端我们称为 公共端 ,剩下的两端分别是输入端和输出端。根据共地端的不同,MOS管具有三种放大器配置,分别是共栅极(CG)、共漏极(CD)、共源极(CS)。
放大器基本参数
在我们继续学习MOS放大器的之前,我们先来了解一些放大器的基本参数。
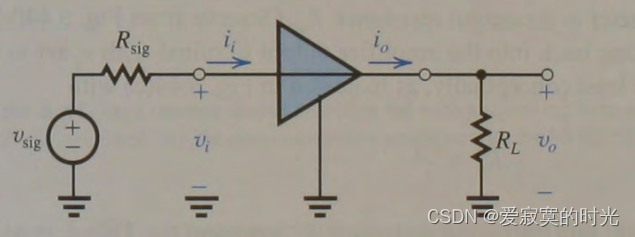
下图是抽象放大器的基本电路,放大器一端共地,信号源 v s i g v_{sig} vsig 具有内阻 R s i g R_{sig} Rsig 接入放大器的输入端,输入电压为 v i v_i vi 输入电流为 i i i_i ii ;放大器输出端和负载电阻 R L R_L RL 相连,输出电压为 v o v_o vo 输出电流为 i o i_o io 。
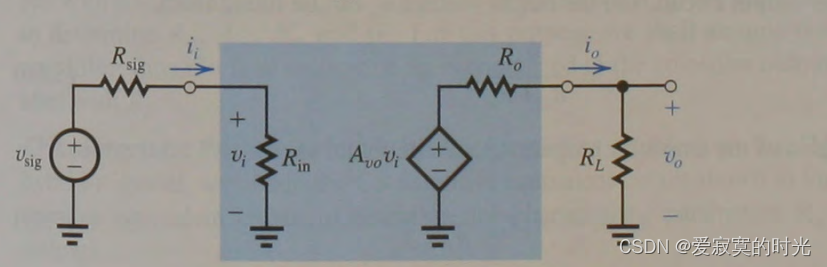
下图是抽象放大器等效电路图,放大器的第一个参数 输入电阻
R
i
n
R_{in}
Rin 代表了放大器的输入特性,定义为:
R i n ≡ v i i i R_{in} equiv frac{v_i}{i_i} Rin≡iivi
信号源内阻和输入电阻构成串联分压,因此:
v i = R i n R i n + R s i g v s i g v_i = frac{R_{in}}{R_{in} + R_{sig}} v_{sig} vi=Rin+RsigRinvsig
我们本章学习的所有放大器都是单边放大器,放大器不包含内部反馈,也就是说
R
i
n
R_{in}
Rin 的值与
R
L
R_L
RL 的值无关。
第二个参数是 开路电压增益 A v o A_{vo} Avo 描述了放大器的放大特性,定义为:
A v o ≡ v o v i ∣ R L = ∞ A_{vo} equiv frac{v_o}{v_i} |_{R_L= infty} Avo≡vivo∣RL=∞
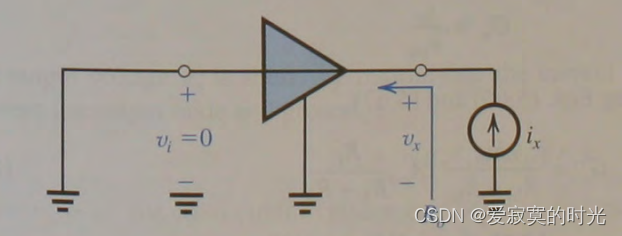
第三参数是放大器的 输出内阻 R o R_o Ro ,输出电阻的定义为,将放大器的输入端接地,负载电路是一个预置电流源 i x i_x ix ,测量输出电压 v x v_x vx 。则输出电压是从输出端看过去的戴维南等效电阻。
R o = v x i x R_o = frac{v_x}{i_x} Ro=ixvx
输出电压
A
v
o
v
i
A_{vo}v_i
Avovi 与输出电阻,负载电阻构成分压电路:
v o = R L R L + R o A v o v i v_o = frac{R_L}{R_L + R_o} A_{vo} v_i vo=RL+RoRLAvovi
则电路的增益为:
A v ≡ v o v i = R L R L + R o A v o A_v equiv frac{v_o}{v_i} = frac{R_L}{R_L + R_o} A_{vo} Av≡vivo=RL+RoRLAvo
电路的整体增益为:
G v ≡ v o v s i g = R i n R i n + R s i g R L R L + R o A v o G_v equiv frac{v_o}{v_{sig}} = frac{R_{in}}{R_{in} + R_{sig}} frac{R_L}{R_L + R_o} A_{vo} Gv≡vsigvo=Rin+RsigRinRL+RoRLAvo
共源极放大器配置
在三大放大器配置中,应用 最广泛的那必然是共源极放大器配置(CS)。一般的,在联级放大器电路设计中共源极放大器起到主要的增益放大作用。
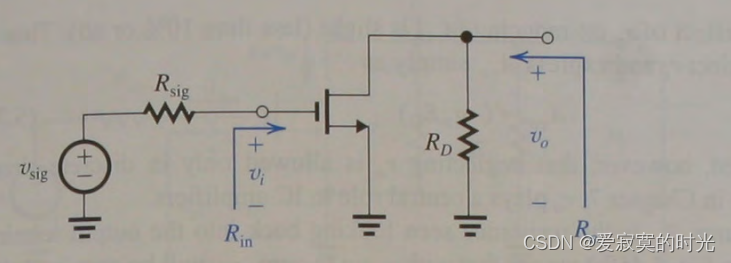
上图就是共源极放大器基本电路(DC已置零),在这里我们直接将
R
D
R_D
RD 当作为放大器电路的一部分,负责电流转电压,如果想单独引入
R
L
R_L
RL 可以和
R
D
R_D
RD 并联。
将放大器电路使用混合 π pi π 模型代替后,得到的电路如下图:
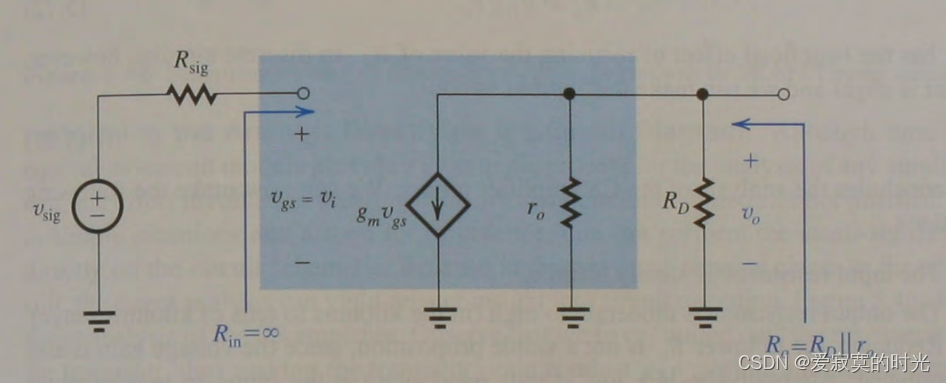
显然,输入电阻阻值无穷大:
R i n = ∞ R_{in} = infty Rin=∞
输出电压为:
v o = − ( g m v g s ) ( R D ∣ ∣ r o ) v_o = -(g_m v_{gs})(R_D || r_o) vo=−(gmvgs)(RD∣∣ro)
因为 v g s = v i v_{gs} = v_i vgs=vi ,则开路增益为:
A v o = − g m ( R D ∣ ∣ r o ) A_{vo} = -g_m (R_D || r_o) Avo=−gm(RD∣∣ro)
注意到 r o r_o ro 的存在,在一般的离散电路中, R D R_D RD 的阻值要比 r o r_o ro 小得多,因此我们可以忽略 r o r_o ro 的存在,简化为:
A v o ≃ − g m R D A_{vo} simeq -g_m R_D Avo≃−gmRD
输出电阻我们可以使用戴维南等效电路观察出,将输入端接地,那么输出端的输出电阻为:
R o = R D ∣ ∣ r o ≃ R D R_o = R_D || r_o simeq R_D Ro=RD∣∣ro≃RD
通过上述分析,总结一下:
- 输入电阻无穷大。
- 输出电阻一般很大(几千欧到几十千欧),但是降低 R D R_D RD 的阻值是不明智的,因为同样会降低电压增益,可以联级一个源极跟随器。
- CS的电压增益通常很大,所以经常作为商用放大器方案中的主要增益单元使用,但是CS有一个缺点是带宽受限。
注意到因为输入电阻无穷大所以 v i = v s i g v_i = v_{sig} vi=vsig ,如果放大器带载,负载电阻为 R L R_L RL ,放大器增益为:
A v = − g m ( R D ∣ ∣ R L ∣ ∣ r o ) A_v = -g_m (R_D || R_L || r_o) Av=−gm(RD∣∣RL∣∣ro)
整体增益为:
G v = A v = − g m ( R D ∣ ∣ R L ∣ ∣ r o ) G_v = A_v = -g_m (R_D || R_L || r_o) Gv=Av=−gm(RD∣∣RL∣∣ro)
带源极电阻的CS放大器
在CS放大器的源极引入一颗电阻 R s R_s Rs ,这将改进CS放大器的性能,如图:
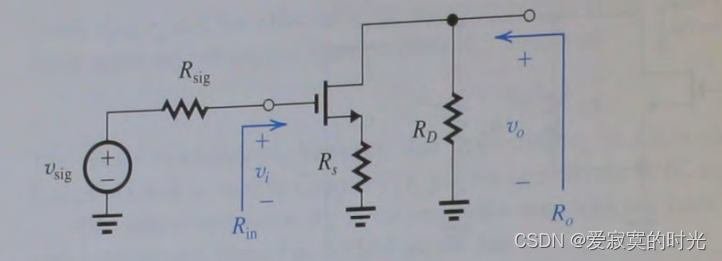
此时用T模型分析这个电路是比较简单的,因为 R s R_s Rs 可以加入到 1 / g m 1/g_m 1/gm 中,如下图,我们在这里忽略 r o r_o ro 的影响:
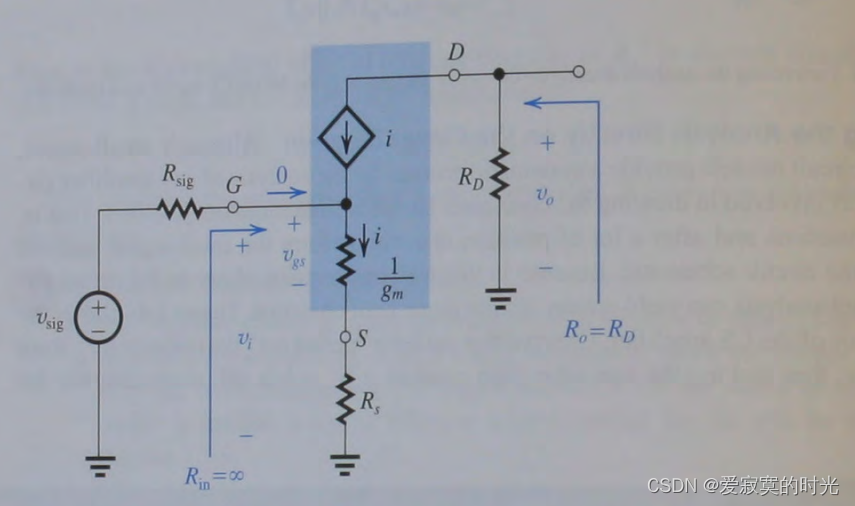
和CS不同的是,输入电压 v i v_i vi 作用于源极电阻 1 / g m + R s 1/g_m + R_s 1/gm+Rs 上,那么 v g s v_{gs} vgs 从 v i v_i vi 中分压:
v g s = v i 1 + g m R s v_{gs} = frac{v_i}{1+g_m R_s} vgs=1+gmRsvi
因此我们能够通过一个电阻 R s R_s Rs 来控制 v g s v_{gs} vgs 的幅值,别让 v g s v_{gs} vgs 太大而让MOS管进入非线性区。这是引入这个电阻的第一个好处。其他好处我们将在其他章节学习,这颗电阻增加了放大器的带宽,同时引入了负反馈机制。如果简单的描述一下负反馈机制:当前保持 v i v_i vi 不变,由于一些原因导致了漏极电流增大,源极电流同样增大,这导致了在 R s R_s Rs 上的电压降增大,因此源极电压增大 V g s V_{gs} Vgs 减小,导致漏极电流减小,形成负反馈回路。
输出电压为 v o = − i R D v_o = -i R_D vo=−iRD,电流 i = ( g m 1 + g m R s ) v i i = (frac{g_m}{1+g_m R_s})v_i i=(1+gmRsgm)vi 。
因此开路电压增益为:
A v o = − R D 1 / g m + R s = − g m R D 1 + g m R s A_{vo} = -frac{R_D}{1 / g_m + R_s} = - frac{g_m R_D}{1 + g_m R_s} Avo=−1/gm+RsRD=−1+gmRsgmRD
这个式子指出,引入源极电阻后,开路电压增益减小了因子 ( 1 + g m R s ) (1 + g_m R_s) (1+gmRs) ,这是引入源极电阻的所需要为出付出的代价。在后面几章,我们将会发现,因子 ( 1 + g m R s ) (1 + g_m R_s) (1+gmRs) 就是负反馈回路的负反馈因子。 R s R_s Rs 也被称为源极退化电阻。
观察式子 i = ( g m 1 + g m R s ) v i i = (frac{g_m}{1+g_m R_s})v_i i=(1+gmRsgm)vi 我们发现括号里面的系数可以当做是引入 R s R_s Rs 之后新的互导系数,因此同时互导系数也减小了因子 ( 1 + g m R s ) (1 + g_m R_s) (1+gmRs) 。根本原因是 v g s v_{gs} vgs 减小了因子 ( 1 + g m R s ) (1 + g_m R_s) (1+gmRs) 。
对于式子 A v o = − R D 1 / g m + R s A_{vo} = -frac{R_D}{1 / g_m + R_s} Avo=−1/gm+RsRD 有一个更强的解释,从栅极到漏极的电压增益等于漏极总电阻除以源极总电阻。
A v g t d = − R D R S A_{vgtd} = -frac{R_D}{R_S} Avgtd=−RSRD
这是一个一般性结论,带入 R s = 0 R_s = 0 Rs=0 得到普通CS放大器的增益。
当引入负载 R L R_L RL 时,整体增益为:
G v = A v = − g m ( R D ∣ ∣ R L ) 1 + g m R s G_v = A_v = -frac{g_m(R_D || R_L)}{1+ g_m R_s} Gv=Av=−1+gmRsgm(RD∣∣RL)
共栅极放大器配置
下图展示了共栅极放大器的基本电路图(DC已置零)。信号源为 v s i g v_{sig} vsig 信号源的内阻为 R s i g R_{sig} Rsig 。因为信号源串联在MOS管的源极,因此采用T模型更好分析。
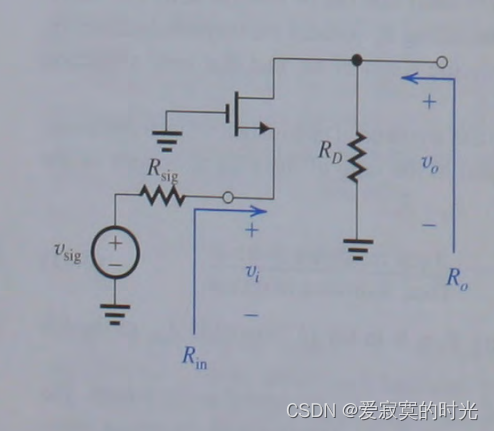
将MOS管使用T模型等效代替后,我们得到下图的电路图(注意到我们忽略了
r
o
r_o
ro ):
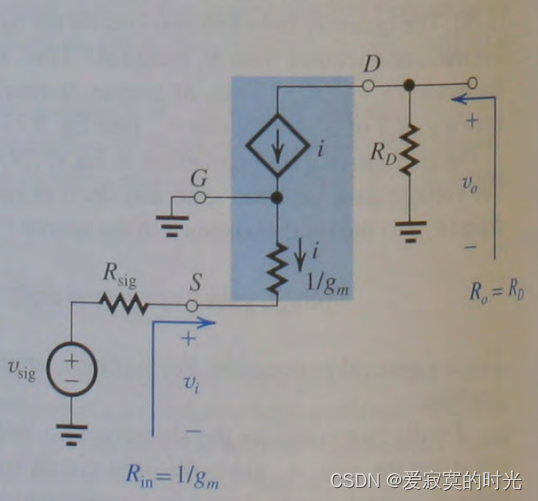
首先考虑放大器的输入阻抗,显然为:
R i n = 1 g m R_{in} = frac{1}{g_m} Rin=gm1
一般情况下 1 g m frac{1}{g_m} gm1 只有几百欧姆,因此CG放大器的输入阻抗很小。
为了计算开路电压增益,我们通过漏极电流得到:
v o = − i R D v_o = -i R_D vo=−iRD
带入电流量 i i i :
i = − v i 1 / g m i = -frac{v_i}{1/g_m} i=−1/gmvi
最终开路电压增益为:
A v o = g m R D A_{vo} = g_m R_D Avo=gmRD
开路电压增益为正,则说明输入信号和输出信号直接无相位差,虽然在绝对值上和CS相同,但是相位差和CS放大器不同。
关于输出阻抗,显然为:
R o = R D R_o = R_D Ro=RD
这一点和CS放大器相同。
虽然开路电压增益绝对值上和CS相同,但是如果考虑到CG的低输入阻抗的特性,就能够遇见得到,CG放大器的整体电压增益要比CS低很多,因为信号源到输入电压存在大量的衰减。通过计算:
v i v s i g = R i n R i n + R s i g = 1 / g m 1 / g m + R s i g frac{v_i}{v_{sig}} = frac{R_{in}}{R_{in} + R_{sig}} = frac{1/g_m}{1/g_m + R_{sig}} vsigvi=Rin+RsigRin=1/gm+Rsig1/gm
如果 R s i g R_{sig} Rsig 远大于 1 / g m 1/g_m 1/gm ,这将导致大量的信号衰减。假设负载电阻为 R L R_L RL 那么整体增益为:
G v = 1 / g m R s i g + 1 / g m [ g m ( R D ∣ ∣ R L ) ] = R D ∣ ∣ R L R s i g + 1 / g m G_v = frac{1/g_m}{R_{sig} + 1/g_m}[g_m(R_D || R_L)] = frac{R_D || R_L}{R_{sig} + 1/g_m} Gv=Rsig+1/gm1/gm[gm(RD∣∣RL)]=Rsig+1/gmRD∣∣RL
注意到,整体增益仍然可以解释为漏极总电阻比源极总电阻。若 R s i g R_{sig} Rsig 和 R D ∣ ∣ R L R_D || R_L RD∣∣RL 有相同的数量级,那么 G v G_v Gv 会非常小。
因为较低的输入阻抗,CG放大器的适用范围很小,通常被设计用来放大具有低内阻的高频信号,或者线缆需要做阻抗特性匹配。在以后的章节我们可以看到,CG放大器具有优秀的频响特性。另外,在后面的章节,我们将看到CG和CS进行组合得到的在集成模拟电路中经典的共源共栅放大器电路。
共漏极放大器配置(源极跟随器)
最后一个放大器配置是共漏极放大器配置,也称为源极跟随器,这是一种相当重要的电路,既可以用来处理小信号放大,也可以用来处理大功率信号的传输。
首先在讲解共漏极放大器配置之前,我们先说明一下为什么需要电压缓冲器,考虑下图的一个情况:
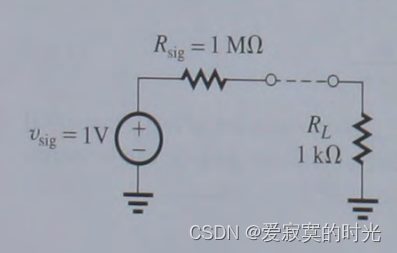
一个具有内阻为1兆欧姆的1V信号源传输到负载阻值为1千欧的电阻上,通过计算我们知道,最终负载得到的信号强度为1毫伏左右,信号在传输中存在大量的信号衰减,一个解决方案就是下图的带有电压缓冲器的传输电路:
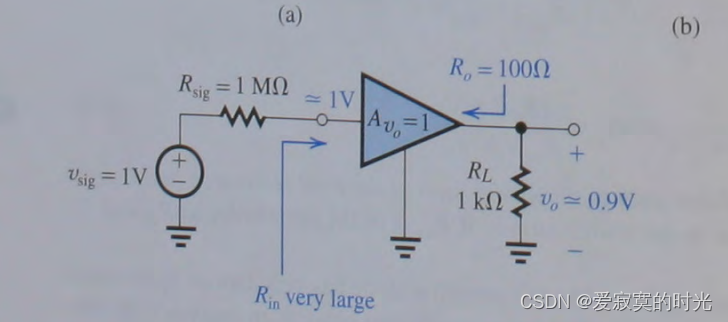
中间是我们引入的电压缓冲器,电压缓冲器其实也是放大器,只不过增益为单位增益
A
v
=
1
A_v=1
Av=1 。这是因为电压缓冲器的目的不是进行信号放大,而是在信号源和负载之间引入一个巨大的输入阻抗
R
i
n
R_{in}
Rin 和一个很小的输出阻抗
R
o
R_o
Ro 。在上图的电路中,最终负载得到的信号强度为0.9伏左右,是一个巨大的改进。
下图是我们共漏极放大器配置的基本电路(DC已置零),因为 R L R_L RL 直接接入源极,使用T模型分析是比较简单的。
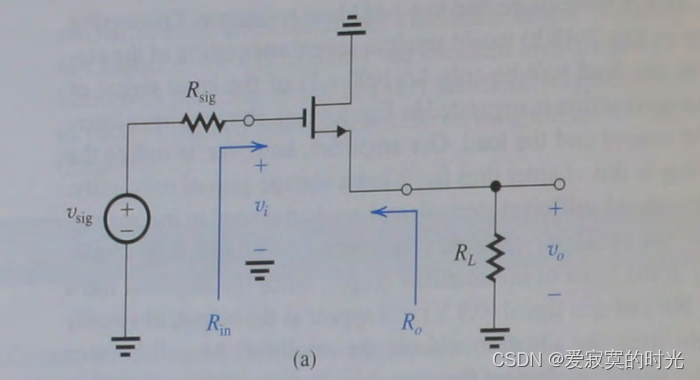
通过将MOS管用T模型等效替代后,我们得到:
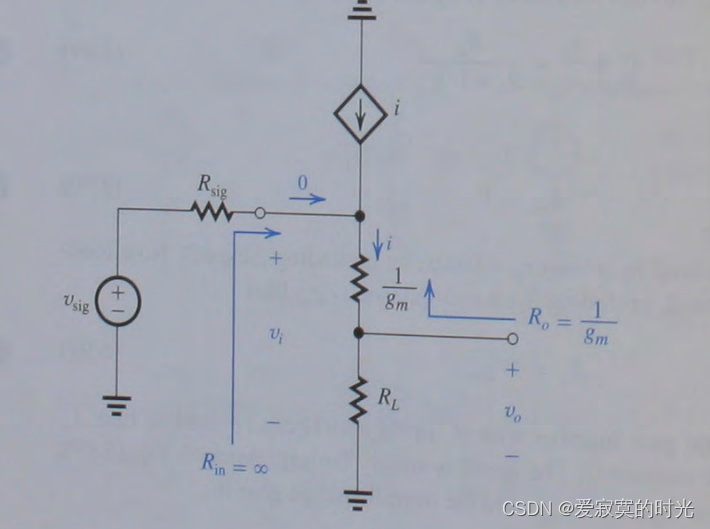
显然输入阻抗为无穷大:
R i n = ∞ R_{in} = infty Rin=∞
对于电压增益,输入信号 v i v_i vi 作用在 R L + 1 / g m R_L + 1/g_m RL+1/gm 上, v o v_o vo 通过分压得到:
A v = R L R L + 1 / g m A_v = frac{R_L}{R_L + 1/g_m} Av=RL+1/gmRL
令 R L = ∞ R_L = infty RL=∞ 得到开路增益:
A v o = 1 A_{vo} = 1 Avo=1
对于输出阻抗显然为:
R o = 1 / g m R_o = 1/g_m Ro=1/gm
整体电压增益为:
G v = A v = R L R L + 1 / g m G_v = A_v = frac{R_L}{R_L + 1/g_m} Gv=Av=RL+1/gmRL
然而,实际上的 G v G_v Gv 稍低于单位增益,只要保证 R L R_L RL 远大于 1 / g m 1/g_m 1/gm 即可看做是单位增益。
增益为单位增益,这说明源极电压等于栅极电压值,电压在源极跟随栅极电压的变化而变化,因此CD放大器也称为源极跟随器。
另外一种负反馈角度的解释是,假设栅极电压增大,那么栅极源极的电压降 V g s V_{gs} Vgs 就会增大,导致 i D i_D iD 增大,进而导致源极电压增大,最终通过负反馈循环源极电压等于栅极电压。
总结一下,CD放大器具有极大的输入电阻,较小的输出电阻,单位增益,正好符合电压缓冲器的定义,因此可以当做是电压缓冲器使用。CD放大器经常在商业放大器方案中作为最后的输出级以降低输出阻抗。
总结
将以上三种基本MOS放大器配置的特性总结一张图如下:

最后
以上就是端庄发卡最近收集整理的关于电子技术——基本MOS放大器配置电子技术——基本MOS放大器配置的全部内容,更多相关电子技术——基本MOS放大器配置电子技术——基本MOS放大器配置内容请搜索靠谱客的其他文章。

![GPS 入门 1 —— 基础知识[转]](https://www.shuijiaxian.com/files_image/reation/bcimg7.png)






发表评论 取消回复