使用差分进化解决多目标优化问题

Multi-Objective Optimization with Modified Pareto Differential Evolution

1.摘要

本文修改了差分进化算法，将其用来解决多目标优化问题，取名为MDE(Modified Pareto Differential Evolution)。并做了如下几点改进：①借用了Niche theory的思想改进了拥挤度机制②引入了一个随时间变化的缩放比例向量F③使用了一个简单且高效的变异因子

2.介绍

说了下进化算法解决多目标问题的好处。

3.差分进化算法介绍

差分进化算法结构和其他进化算法类似。基本的操作也是：初始化，变异，交叉，混合父子代，选择更优的个体。对比其他进化算法只是将变异提前了。

变异操作
对于每个个体Xig(我们称其为目标向量)，有如下5个变异方式进行选择。

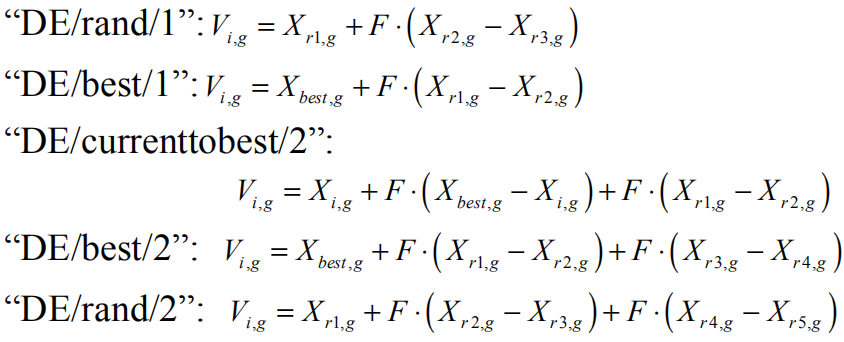
Vig代表变异后的个体向量，其中指数r1、r2、r3、r4、r5是在1~Np范围内随机产生且相互不同的整数。 F是[0,2]范围的缩放比例向量，Xbest是种群中具有最佳适应度值的个体向量(注意这是在说传统的单目标进化算法)。
不同算法中指数r1、r2、r3、r4、r5设定的值也不一样，本文用了上面5中策略的第一种，详见后文。

交叉操作

在变异阶段之后，将“二进制”交叉操作应用于生成的变异向量Vig及其相应的目标向量Xig，以生成一个试验向量，方式如下：

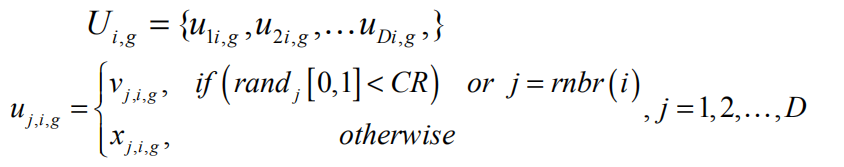
其中CR是交叉概率；*rnbj(i)*是向量维度D内的一个随机正整数，其作用是保证交叉后的向量和目标向量至少有一个决策变量不相等；uj,i,g表示我们得到的试验向量，也可理解为子代。

选择操作
方式如下，将刚才产生的试验向量Uj,i,g与原目标向量Xi,g进行比较,保留目标函数更优的。

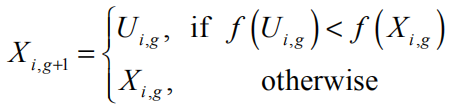
4.MDE详细介绍

精英非支配排序遗传算法NSGA-Ⅱ

这里不对NSGA-Ⅱ做详细介绍了，不懂的可以去本站上搜其他人的博客看。MDE是建立在这个算法基础上的。

改进的拥挤度机制------摘要提出的第一个创新
原文用两目标优化问题举例,下图是解A~F在目标空间上的展示。

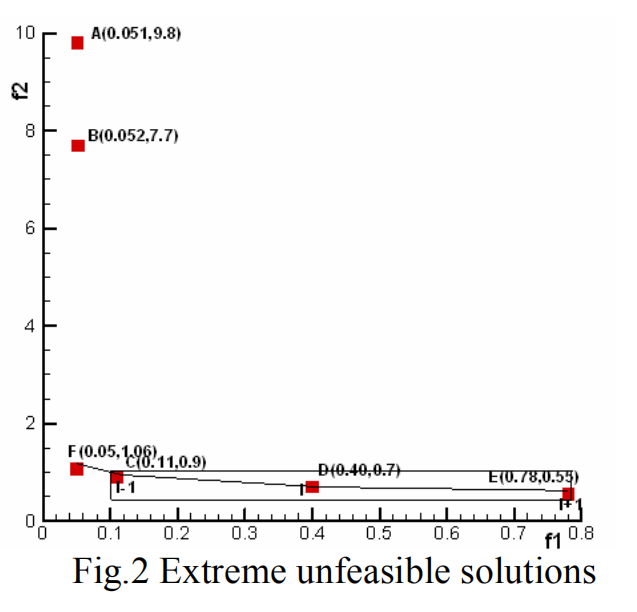
根据定义，解A和E的拥挤距离为无穷大，解B的拥挤距离为8.92，解D的拥挤距离为0.76。当这些点在同一层时， 我们会保留所有点，这显然是不恰当的，因为虽然一个目标值几乎相同，但另一个目标值是六比一。因此本文提出下面的方式进行处理。

A,B为两个个体，ε是个很小的数，在这里充当阈值，保证A和B在f1相差无几的情况下只保留一个。这样的好处是淘汰掉一些没必要的解。
修改后的变异策略------摘要提到的第二个创新

本文使用了前文提到的DE/rand/1策略，为了让每个父代都有机会进入子代，取r1=i，即。

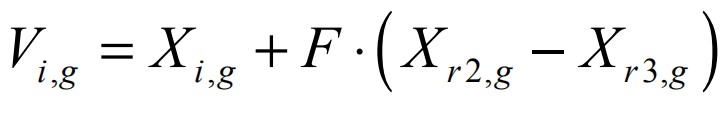
为了进行探索，r2和r3仍然是随机选择的，但遵循Xr2,g比Xi,g“更好”，而Xr3,g比Xi,g“更差”，“更好”意味着Xr2,g的秩比Xi,g更高或Xr2,g的拥挤距离更大。这样子可以起到一个将解引导向更好的方向的效果。

修改后的F------摘要提到的第三个创新
与种群大小Np一样，F必须高于一定的临界值，以避免过早收敛到次优解，但如果F变得太大，寻找最优的函数评估的数量很快就会增长。 通常，0.4<F<0.9，F=0.9是收敛速度和概率之间的一个很好的折衷。 为了加快DE算法的收敛速度，引入了时间变量F，它随时间线性变化如下：

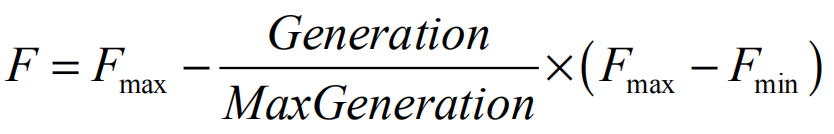
其中Generation是当前迭代次数，Max Generation是允许的最大迭代次数，Fmax，Fmin分别表示权重的最大值和最小值。
因此，该算法从0代F=Fmax开始，随着迭代次数的增加，F逐渐下降，最后F会等于Fmin。在开始时，大的F使得搜索向单个点的搜索空间减少，这样会强调全局搜索，帮助DE避免局部最优。之后，随着F的下降，F会在最优处进行局部搜索。 显然，要在算法的探索和开发能力之间取得平衡，就必须明智地选择Fmax和Fmin。 本文将Fmax设置为0.9，Fmin设置为0.4。

5.实验结果

本文采用MOEA里常用的五个ZDT测试函数做实验。

实验指标
指标γ
本文用到两个指标，第一个指标γ度量收敛到已知的帕累托最优解集的程度。下图显示了这个指标的计算过程。

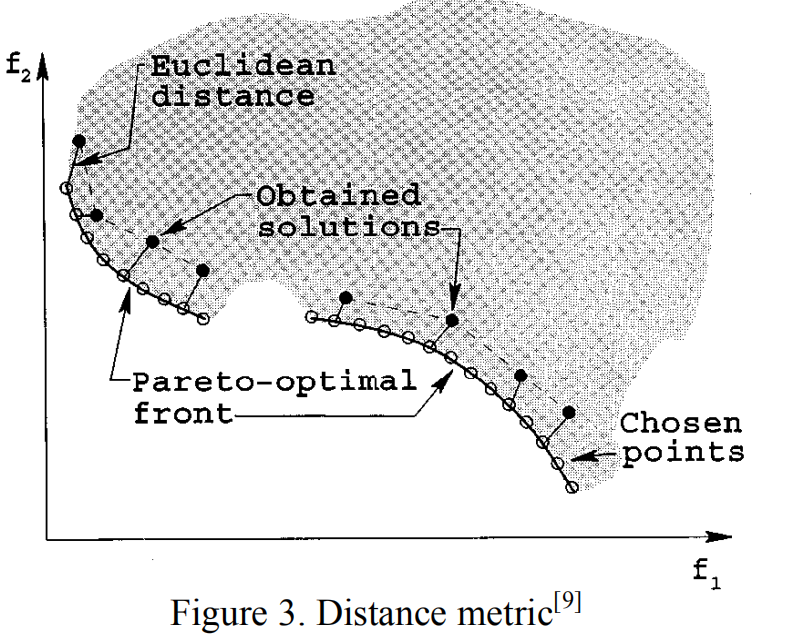
假设通过算法得到的Pareto前沿为Z，实际上Pareto前沿为Z’0。公式为：

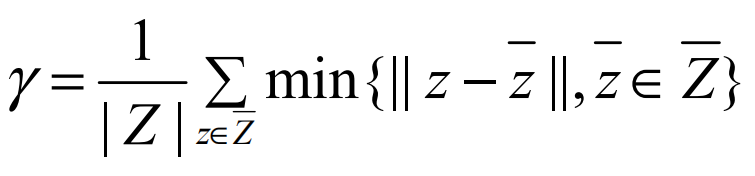
显然，γ值越小，算法逼近Pareto最优集越好。

指标Δ
第二个指标Δ度量所获得的解的分布情况。

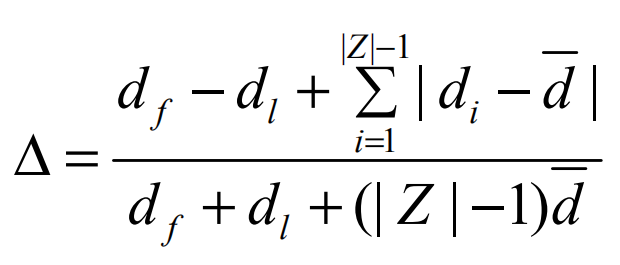
距离d如下图所示。参数df和dl是得到的非支配集的极值解和边界解之间的欧氏距离。 Δ值越小，帕累托解的多样性越好。

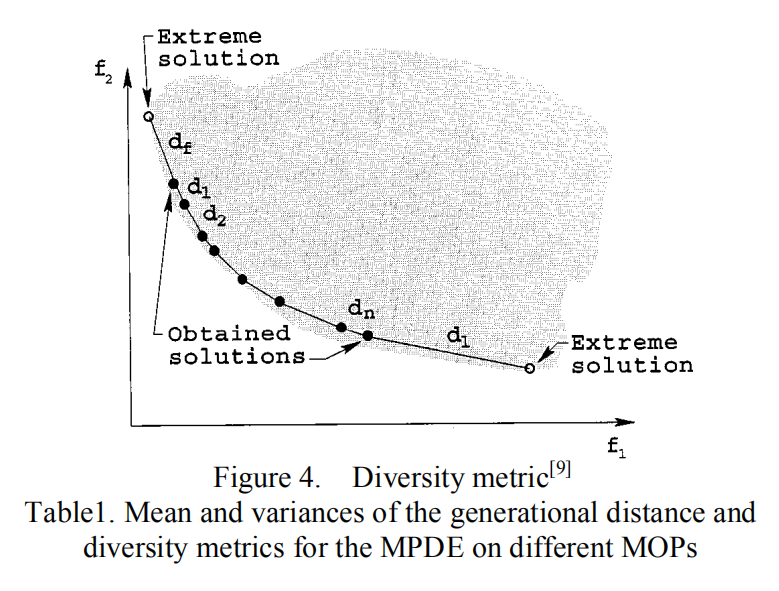
实验结果

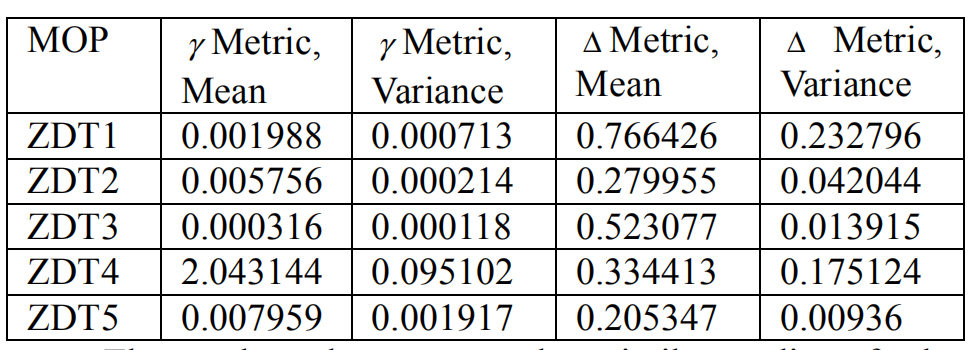
结果表明，与其他算法的类似研究( Multiobjective optimization using a Pareto differential evolution approach)相比，该算法在ZDT1、ZDT2、ZDT3和ZDT5上具有较好的效果。 上表显示，对于ZDT4，距离度量γ值相对较大，表明该算法在收敛到真正的Paretofront方面存在困难。 部分原因是因为所有函数的参数设置都是相同的，经验表明，当缩放因子F和CR的范围发生变化时，ZDT4的结果可以得到改善。

6.总结

本文提出了一种基于DE/Rand/1版本的多目标差分进化算法。 首先，引入Niche理论，改进了拥挤机制。 改进的DE方法引入了一个时变标度因子F，并使用了一个简单但有效的突变算子，它结合了种群中较好和较差的解的信息。本文通过对五个ZDT检验函数的检验和其他MOEA检验结果的比较和分析，证明了该算法的有效性。

返回受约束的多目标优化问题优秀论文及总结目录

最后

以上就是开朗小松鼠为你收集整理的使用差分进化解决多目标优化问题的全部内容，希望文章能够帮你解决使用差分进化解决多目标优化问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。