时间序列分析（10）| 传递函数模型和ADL模型402 Payment Required402 Payment Required402 Payment Required402 Payment Required

83 阅读 0 评论 55 点赞

我是靠谱客的博主可耐小笼包，这篇文章主要介绍时间序列分析（10）| 传递函数模型和ADL模型402 Payment Required402 Payment Required402 Payment Required402 Payment Required，现在分享给大家，希望可以做个参考。

「说明」：本文昨天推送时，将几个以图片形式插入的公式弄混了，今天修改后重发。

传递函数模型是对干扰模型的拓展，而自回归分布滞后模型（autoregressive distributed lag model，ADL模型）则是传递函数模型的一个特例。

1 传递函数模型

1.1 一般形式

上篇介绍到干扰模型的形式如下：

以及滞后形式：

402 Payment Required

而传递函数的一般形式如下：

402 Payment Required

其中，同、一样都是滞后算子的多项式，称作「传递函数」（transfer function）。

1.2 与干扰模型的比较

干扰模型和传递函数模型的共同点是都假定为外生变量，即只允许影响，而不允许反过来影响。

从形式上看，传递函数模型更具一般性：对于干扰模型，无论是当期值，还是滞后值，都仅含一项与相关的项，而传递函数模型则允许出现分布式滞后项。

从外生变量的内涵上看，二者也存在区别：

干扰模型中的外生变量所表示的因素是“突然”出现的，进而把序列分成了干扰前和干扰后两段；它也可能会“突然”消失（即外生变量恢复为0），或者持续存在；从形式上看，它一般使用指示变量表示，如虚拟变量数值只是表示两种状态，而不具有实际的大小意义；
传递函数模型的外生变量可以是与被解释变量同时存在的时间序列变量；它可以为任意的形式，也可以有明确的实际意义，如空气污染浓度（或其转换值）可以作为解释平均寿命随时间变化的外生变量。

2 ADL模型

ADL模型是传递函数模型的特例。令，模型形式如下：

402 Payment Required

此时，模型中仅含有的自回归项和分布式滞后项，不含误差的移动平均项，因此称为「自回归分布滞后模型」（ADL模型）。

3 模型参数的估计

3.1 互相关函数

给定值，序列与之间的相关系数称为「互相关系数」，使用表示，它与之间的关系称为「互相关函数」（cross-correlation function, CCF）。

设定一个特殊形式的传递函数模型：

这个形式与干扰模型类似，但的内涵有所不同，这里设定它为白噪音序列（而非像干扰模型那样的虚拟变量）。

根据理论推导，可得，

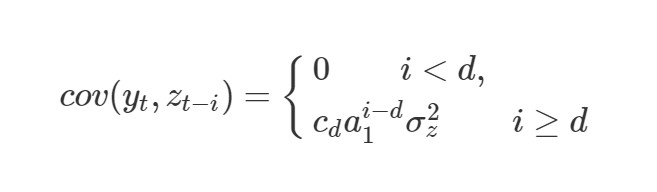
将互相关系数的分母改写成，得到「标准化协方差函数」（cross-covariance function, CCVF），使用表示。显然，CCF和CCVF存在比例关系，因此二者可以混用。

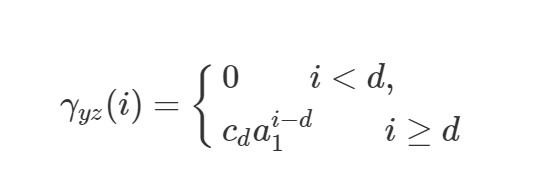
上式具有如下规律：

首个不为0的元素恰好对应中首个系数不为0的滞后项；
当时，呈指数衰减，衰减比例为，这与所对应的过程的自相关函数（ACF）变化趋势完全一致。

当向模型中再加入一个的滞后项（系数设定为），即改变的形式时，的理论形式如下：

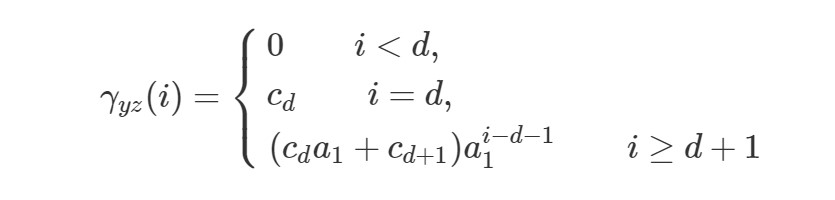
对于上式，前面的规律仍然适用：当时，CCVF呈指数衰减，衰减比例为。

当向模型中加入的滞后项（系数设定为），即改变的形式（保持不变）时，存在如下关系：

上式所刻画的的变化趋势与所对应的过程的ACF变化趋势也完全一致。

拓展地看，当为白噪音序列时，CCVF从某一滞后期后的变化趋势能够大致反映出的形式。

此外，CCVF也能大致反映的形式：CCVF的第一个非零值与的第一个非零滞后项相对应；其峰值（取绝对值）在最大滞后项附近（当直接衰减时，二者正好对应；当震荡衰减时，峰值可能在最大滞后项之后一点出现）。

在R语言中，可以使用基础包stats中的ccf()函数计算CCF或CCVF。

acf(x, lag.max = NULL,
    type = c("correlation", "covariance", "partial"),
    plot = TRUE, na.action = na.fail, demean = TRUE, ...)

当type参数设定为correlation时，计算的是CCF；设定为covariance，计算的是CCVF。

3.2 滤波

通过上一节，我们知道可以通过CCF或CCVF判断出和的阶数，但是这一结论是在为白噪音序列的前提下推导的，更一般的情况是假设它为一个平稳ARMA过程。可以使用下式进行表示：

其中、为滞后算子多项式，为白噪音序列。

转换后得，。进而有，

令，则上式可转换为如下形式：

这样，传递函数模型中的外生变量就转换成白噪音的形式了（即）。对和求互相关函数，其变化趋势仍能反映出原始模型中、的形式。

称为「滤波」（filter）；是经过滤波后的值，称为「新息」（innovation）。

在R语言中，基础包stats中的filter()函数能够计算给定序列的滤波值。

该函数与dplyr工具包中很常用的样本筛选函数filter()同名，但功能大不一样。

假设的阶数为，的阶数为，那么就可以称滤波阶数为。此时，传递函数模型可以写成如下形式：

注意，上式中的参数和并不等于和中滞后算子的系数。

3.3 对残差的估计

现在，模型中只剩下残差未被估计了，将它看作是一个ARMA过程，并假设其阶数为，则有

代入模型表达式得，

402 Payment Required

以上步骤对三部分的参数是分别进行估计的，最后可以在上述形式下对这些参数同时进行估计。

4 R中的函数与案例

4.1 函数介绍

基础包stats中的arima()函数并不能对传递函数模型进行估计。可使用的函数是TSA工具包中的arimax()函数，语法结构如下：

arimax(x, order = c(0, 0, 0), 
       seasonal = list(order = c(0, 0, 0), period = NA),
       xreg = NULL, include.mean = TRUE, 
       transform.pars = TRUE, fixed = NULL, 
       init = NULL, method = c("CSS-ML", "ML", "CSS"), 
       n.cond, optim.control = list(),
       kappa = 1e+06, io = NULL, 
       xtransf, transfer = NULL)

该函数是在arima()的基础上改进的。对比可以发现，它只比后者多两个参数：

xtransf：外生变量；
transfer：传递函数的形式，使用滤波阶数表示。

在估计传递参数模型时，order参数是指残差序列的阶数。

此外，TSA工具包中也有一个arima()函数，其功能与arimax()完全一致。

4.2 案例1

本案例中的示例数据可在公众号后台发送关键词「示例数据」获取，文件名132.italy.xls。

library(readxl)
data <- read_xls("132.italy.xls")
data$ENTRY <- paste(rep(1971:1988, each = 4), 1:4, sep = "-")
y = data$Slitaly
z = data$Attkit

ccf(y,z)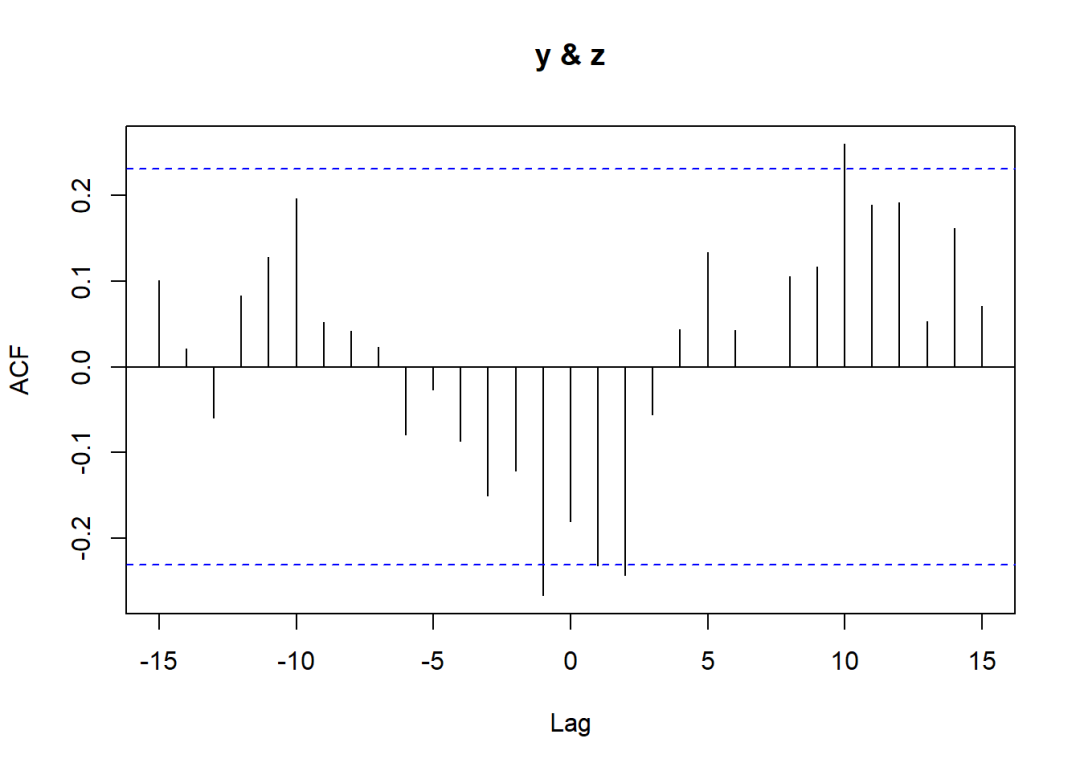

本案例的具体推演步骤见参考书原文。现已知残差序列的阶数为ARMA(2,4)，的阶数为2，的阶数为1；部分滞后项系数为0。使用arimax()函数的估计代码如下：

library(TSA)
arimax(y, order = c(2,0,4),
       xtransf = z,
       transfer = list(c(2,1)),
       fixed = c(NA, NA, 0, 0, 0,NA,0, NA, NA, 0, NA),
       method = "ML")

## arimax(x = y, order = c(2, 0, 4), fixed = c(NA, NA, 0, 0, 0, NA, 0, NA, NA, 
##     0, NA), method = "ML", xtransf = z, transfer = list(c(2, 1)))
## 
## Coefficients:
##          ar1     ar2  ma1  ma2  ma3     ma4  intercept  T1-AR1   T1-AR2  T1-MA0
##       0.4748  0.2873    0    0    0  0.2673          0  0.8948  -0.7751       0
## s.e.  0.1130  0.1164    0    0    0  0.0991          0  0.0968   0.1075       0
##        T1-MA1
##       -0.0023
## s.e.   0.0009
## 
## sigma^2 estimated as 0.005204:  log likelihood = 85.28,  aic = -158.56

模型输出结果的含义如下：

ar1、ar2等对应、等；
ma1、ma2等对应、等；
T1-AR1、T1-AR2对应、等；
T1-MA0、T1-MA1对应、等。

4.3 案例2

上篇已经介绍，估计干扰模型时可以将外生变量赋值给xreg参数。因为干扰模型是传递函数模型的特例，因此它也可以使用估计传递函数模型的方法进行估计，即将外生变量赋值给xtransf，滤波阶数设置为(0,0)。

仍然使用上篇的示例数据，使用两种方法分别进行模型估计。

以传递函数模型的形式进行估计：

data <- read_xls("131.Terrorism.XLS")
data$ENTRY <- paste(rep(1970:2010, each = 4), 1:4, sep = "-")
y2 = data$Transnational
z2 = rep(0, 164)
z2[113:164] <- 1

arimax(y2, order = c(2,0,0), 
       xtransf = z2, transfer = list(c(0,0)),
       method = "ML")  
## arimax(x = y2, order = c(2, 0, 0), method = "ML", xtransf = z2, transfer = list(c(0, 
##     0)))
## 
## Coefficients:
##          ar1     ar2  intercept    T1-MA0
##       0.3421  0.3903    28.6925  -14.8443
## s.e.  0.0719  0.0724     2.9501    4.6322
## 
## sigma^2 estimated as 79.27:  log likelihood = -591.63,  aic = 1191.27

以干扰模型的形式进行估计：

arima(y2, order = c(2,0,0), xreg = z2,
      method = "ML")
## arima(x = y2, order = c(2, 0, 0), xreg = z2, method = "ML")
## 
## Coefficients:
##          ar1     ar2  intercept      xreg
##       0.3423  0.3902    28.7033  -14.8618
## s.e.  0.0718  0.0724     2.9509    4.6336
## 
## sigma^2 estimated as 79.27:  log likelihood = -591.63,  aic = 1191.27