【主动声呐】——匹配滤波器

背景知识

注意频谱密度和频谱的概念一般不作区分！

• 能量谱
  能量信号频谱的平方
  $$S(f)=\int s(t)e^{-j2\pi ft}\mathrm{d}\mathrm{t}$$
  $$G(f)=|S(f){|}^2$$
  频率$f$对应的能量为：
  $$\mathrm{d}{\mathrm{E}}_{\mathrm{f}}=\mathrm{G}(\mathrm{f})\mathrm{d}\mathrm{f}$$
• 功率谱
  功率信号频谱的平方除时间
  $$P(f)=\underset{T\to +\infty }{\lim }\frac{1}{T}|S(f){|}^2$$
  功率信号的功率为
  $$P=\int P(f)\mathrm{d}\mathrm{f}$$
• 帕斯瓦尔定理
  信号的总能量既可以在时间域求积分得到，也可以频域中求积分得到（功率同理）：
  $$W=\int s(t)\mathrm{d}\mathrm{t}=\frac{1}{2\pi }\int \mathrm{S}(\omega )\mathrm{d}\omega$$
• 维纳辛钦定理
  信号的自相关函数与功率谱是傅里叶变换对关系
  $$P(\omega )=\int R(t)e^{-j\omega t}\mathrm{d}\mathrm{t}$$

匹配滤波器

基本准则

使滤波器输出的时域信号能在某一时刻，取到最大的信噪比，然后在该时刻进行判决
（通过滤波器输出的信号即可认为是输入信号和输出信号的相关函数，判决时刻可认为是两者波形重合的时刻）

匹配滤波器的频域表达式

设主动声呐发出的信号为$s(t)$，噪声的功率谱密度为$\frac{n_0}{2}$，滤波器的输出为$y(t)=s_0(t)+n_0(t)$
滤波器输出信号部分$s_0(t)$可表达为：
$$s_0(t)=\frac{1}{2\pi }\int S_0(\omega )e^{j\omega t}\mathrm{d}\omega =\frac{1}{2\pi }\int S(\omega )H(\omega )e^{j\omega t}\mathrm{d}\omega$$
噪声的平均功率可表达为：
$$N_0=\frac{1}{2\pi }\int P_0(\omega )\mathrm{d}\omega =\frac{1}{2\pi }\int P(\omega )|H(\omega ){|}^2\mathrm{d}\omega =\frac{n_0}{4\pi }\int |H(\omega ){|}^2\mathrm{d}\omega$$
输出信号的瞬时功率与噪声平均功率的比值即为信噪比，要找到使它达到最大的时刻$t_0$：
$$r_0=\frac{|s_0(t_0){|}^2}{N_0}=\frac{|\frac{1}{2\pi }\int S(\omega )H(\omega )e^{j\omega t_0}\mathrm{d}\omega {|}^2}{\frac{n_0}{4\pi }\int |H(\omega ){|}^2\mathrm{d}\omega }$$
根据施瓦兹不等式可知：
$$|\frac{1}{2\pi }\int S(\omega )H(\omega )e^{j\omega t_0}\mathrm{d}\omega {|}^2\le \frac{1}{2\pi }|\int H(\omega ){|}^2\mathrm{d}\omega \times \int |S(\omega )e^{j\omega t_0}{|}^2\mathrm{d}\omega$$
等号取到条件为：
$$H(\omega )=K(S(\omega )e^{j\omega t_0}{)}^{\ast }$$
信噪比可化简为：
$$r_0=\frac{\frac{1}{2\pi }\int |S(\omega ){|}^2\mathrm{d}\omega }{\frac{n_0}{2}}=\frac{2E}{n_0}$$
注：此时$H(\omega )=K{S}^{\ast }(\omega )e^{-j\omega t_0}$，通过该滤波器的信号在$t=t_0$的时候取到最大的信噪比

匹配滤波器的冲激响应

根据匹配滤波器的频域表达式$H(\omega )=K{S}^{\ast }(\omega )e^{-j\omega t_0}$，利用傅里叶反变换可以求得匹配滤波器的冲激响应$h(t)$：
$$h(t)=\frac{1}{2\pi }\int H(\omega )e^{j\omega t}\mathrm{d}\omega =\frac{1}{2\pi }\int K{S}^{\ast }(\omega )e^{-j\omega t_0}{e}^{j\omega t}\mathrm{d}\omega =\frac{K}{2\pi }{s}^{\ast }(t_0-t)=\frac{K}{2\pi }s(t_0-t)$$
即匹配滤波器的单位冲激响应为$h(t)=Ks(t_0-t)$
注：
1.这里的$t_0$是自己取的，直接决定了滤波器的形式，同时决定了输出信号的最大信噪比的时刻。
2.为了使滤波器是一个因果系统，则$h(t)=0,t\le 0$，故$s(t)=0,t\ge t_{0}ort\le 0$，即主动声呐发出的信号需为一个短时脉冲。
3.若信号脉宽为$T$，则需要满足$t_0\ge T$，一般取$t_0=T$使滤波器作最小的延时。

匹配滤波器的输出

根据冲激响应的性质，匹配滤波器的输出可以表示为冲激响应与输入信号的卷积：
$$s_0(t)=s(t)\ast h(t)=\int h(\tau )s(t-\tau )\mathrm{d}\tau =\int Ks(t_0-\tau )s(t-\tau )\mathrm{d}\tau$$

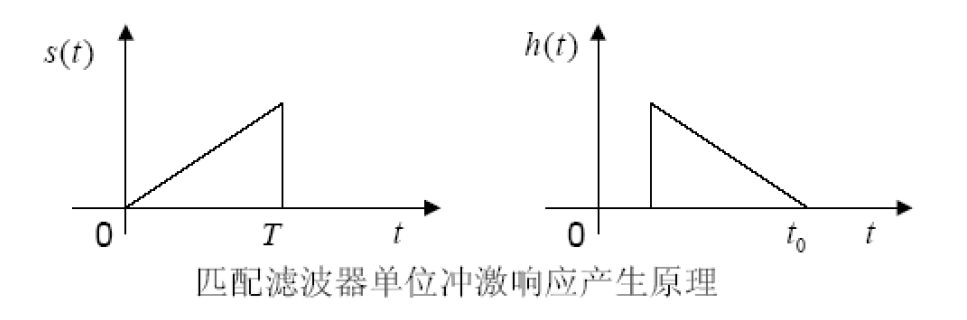
根据上图，可以发现如果$t_0=T$时，$h(t)$翻转后直接就可以得到有效的输出信号，否则还需要进行滑动，直到滑动了一段距离后才能得到有效(不为0)的输出信号。
可以得到输出信号的表达式：
$$r(t)=KR(t-t_0)$$
即为输入信号的自相关函数，故在$t=t_0$时取到最大，故在这个时候进行判决。

最后

以上就是沉静小鸭子为你收集整理的【主动声呐】——匹配滤波器的全部内容，希望文章能够帮你解决【主动声呐】——匹配滤波器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。