麦克纳姆轮底盘运动学模型

1.麦克纳姆轮

麦轮一般是四个一组使用，两个左旋轮，两个右旋轮。左旋轮和右旋轮呈手性对称。

麦克纳姆轮由两大部分组成：轮毂和辊子（roller）。

• 轮毂：整个轮子的主体支架
• 辊子：安装在轮毂上的鼓状物
• 轮毂轴与辊子转轴呈 45° 角
  

麦轮底盘能够实现前后进退、左右平移、原地自转等多种方向的运动。

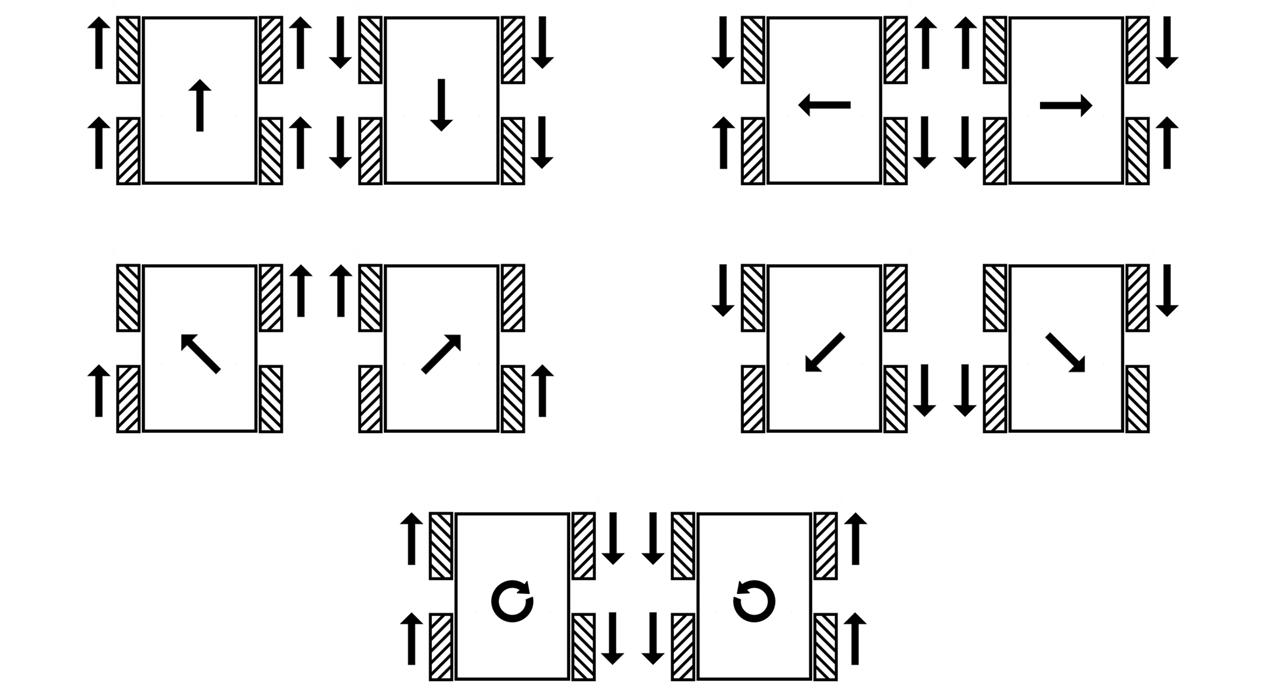
麦轮有四种安装方式：X-正方形（X-square）、X-长方形（X-rectangle）、O-正方形（O-square）、O-长方形（O-rectangle）。

其中 X 和 O 表示的是与四个轮子地面接触的辊子所形成的图形；正方形与长方形指的是四个轮子与地面接触点所围成的形状。

• X-正方形：轮子转动产生的力矩会经过同一个点，所以 yaw 轴无法主动旋转，也无法主动保持 yaw 轴的角度。一般几乎不会使用这种安装方式。
• X-长方形：轮子转动可以产生 yaw 轴转动力矩，但转动力矩的力臂一般会比较短。这种安装方式也不多见。
• O-正方形：四个轮子位于正方形的四个顶点，平移和旋转都没有任何问题。受限于机器人底盘的形状、尺寸等因素，这种安装方式虽然理想，但可遇而不可求。
• O-长方形：轮子转动可以产生 yaw 轴转动力矩，而且转动力矩的力臂也比较长。是最常见的安装方式。

2.麦克纳姆轮底盘运动学模型

以O-长方形的安装方式为例，四个轮子的着地点形成一个矩形。

底盘中心运动分析

麦轮底盘的运动是刚体的运动，为全驱动模型。

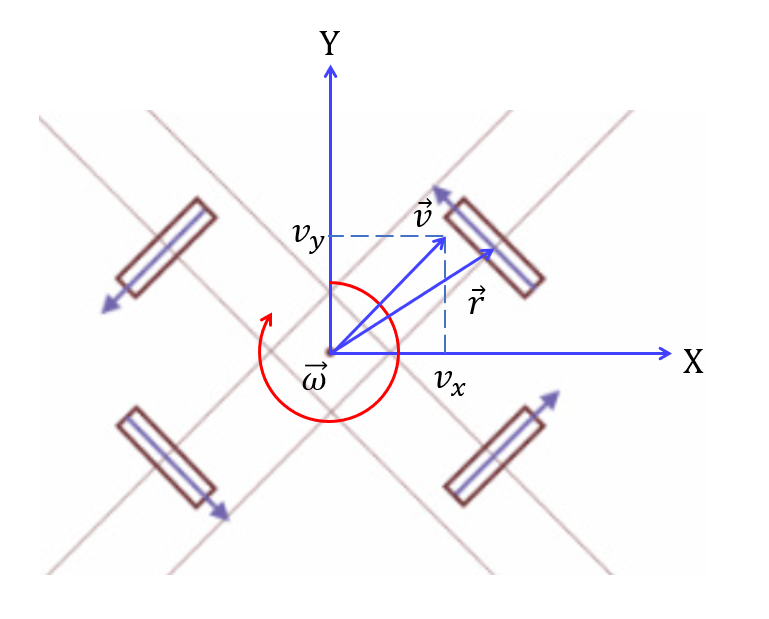
• 底盘中心线速度：$\overrightarrow{v}$
• 底盘中心角速度：$\overrightarrow{\omega }$
• 底盘中心指向轮子轴心向量：$r$

对底盘线速度进行分解，可以得到$v_y和v_x$。

轮子轴心分析

取右上角轮子进行演示分析，如下图所示。

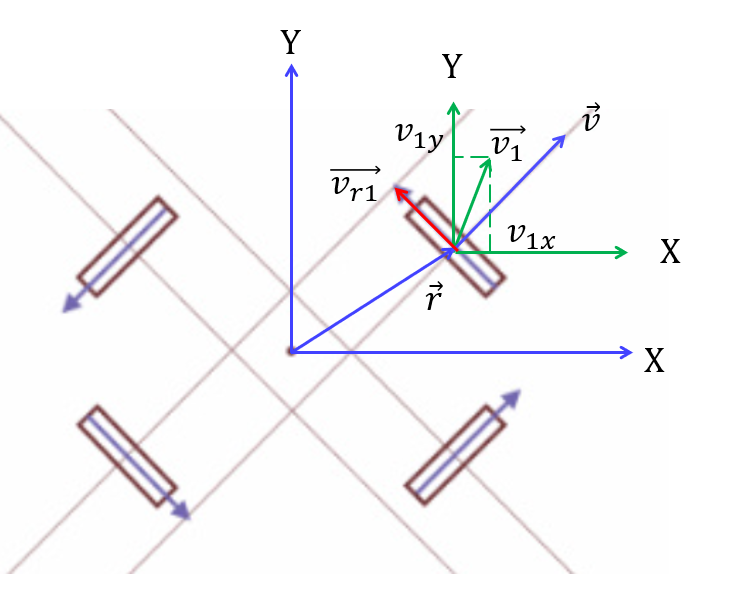
• 底盘一号轮子轴心速度：$\overrightarrow{v_1}$
• 底盘一号轮子轴心沿垂直于$\overrightarrow{r}$方向的速度分量：$\overrightarrow{v_{r1}}$

已知底盘的运动为刚体运动，满足如下公式：
$$\overrightarrow{v_1}=\overrightarrow{v}+\overrightarrow{\omega }\times \overrightarrow{r}$$
则底盘一号轮子在$X$轴和$Y$轴方向上的分量如下，其中，$r_x、r_y$为向量$\overrightarrow{r}$在在$X$轴和$Y$轴方向上的分量。
$$\{\begin{array}{l}\overrightarrow{v_{1x}}=\overrightarrow{v_x}-\omega \cdot r_y\\ \overrightarrow{v_{1y}}=\overrightarrow{v_y}+\omega \cdot r_x\end{array}$$
同理，可以算出其它三个轮子轴心的速度。

辊子分析

根据轮子轴心的速度，可以将其按照轮子接触地面的辊子方向（平行、垂直）进行分解。

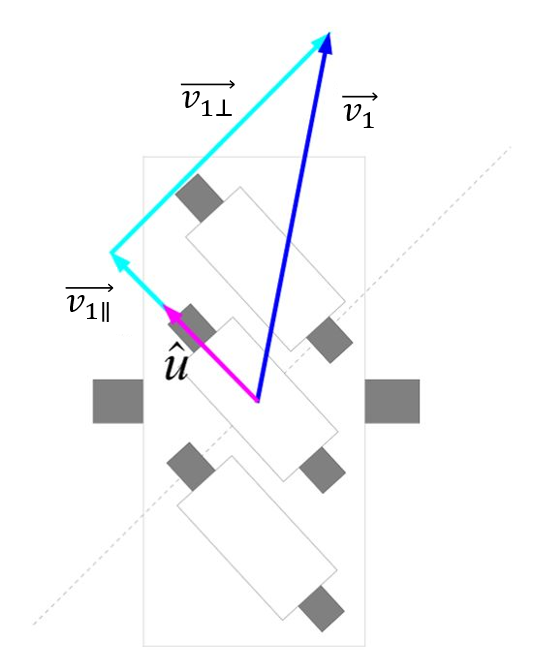
• 底盘一号轮子轴心的速度：$\overrightarrow{v_1}$
• 底盘一号轮子接触地面处辊子方向的单位矢量：$\hat{u}$

垂直辊子方向的速度分量$\overrightarrow{v_{1\perp }}$对轮子转速没有贡献，可以忽略不记。此处仅考虑平行于辊子方向的速度分量$\overrightarrow{v_{1\Vert }}$。

对于单位向量$\hat{u}$，由于辊子以$45°$方式安装在轮毂上，故而可将其分解为：$\hat{u}=-\cos 45°\hat{i}+\cos 45°\hat{j}$。其中$\hat{i}$和$\hat{j}$表示$X$轴方向和$Y$轴方向上的单位向量。

已知一号轮子轴心速度的分解：$\overrightarrow{v_1}=v_{1x}\cdot \hat{i}+v_{1y}\cdot \hat{j}$，则：
$$\begin{gathered} \overrightarrow{v_{1\Vert }}=\overrightarrow{v_1}\cdot \hat{u}=(v_{1x}\cdot \hat{i}+v_{1y}\cdot \hat{j})\cdot (-\cos 45°\hat{i}+\cos 45°\hat{j}) \\ \overrightarrow{v_{1\Vert }}=-\frac{\sqrt{2}}{2}{v}_x+\frac{\sqrt{2}}{2}{v}_y \end{gathered}$$

轮子速度分析

对轮子，设平行于$Y$轴正方向（车辆前进方向）的速度分量为$\overrightarrow{v_{\omega }}$，该速度与辊子夹角$45°$

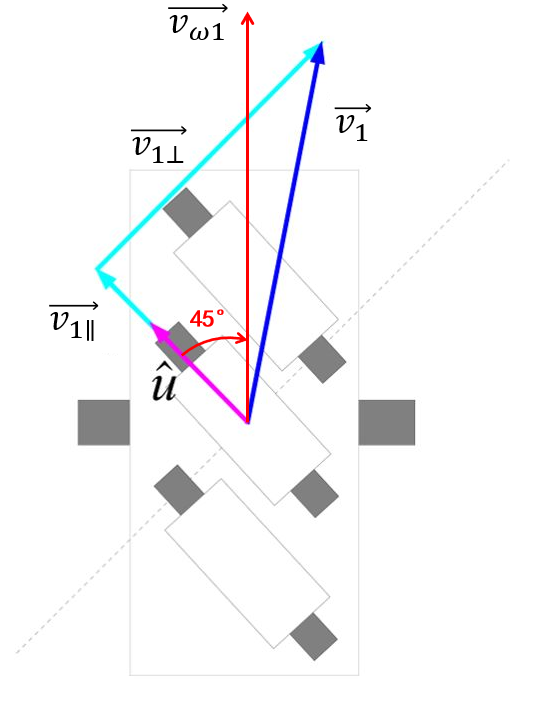
由辊子速度即可得到轮子的转速：
$$v_{\omega 1}=\frac{\overrightarrow{v_{1\Vert }}}{\cos 45°}=-v_x+v_y$$

整合分析

将上述步骤分别对四个轮子进行，设$\overrightarrow{r}$在$X$轴和$Y$轴分量分别为$a、b$。

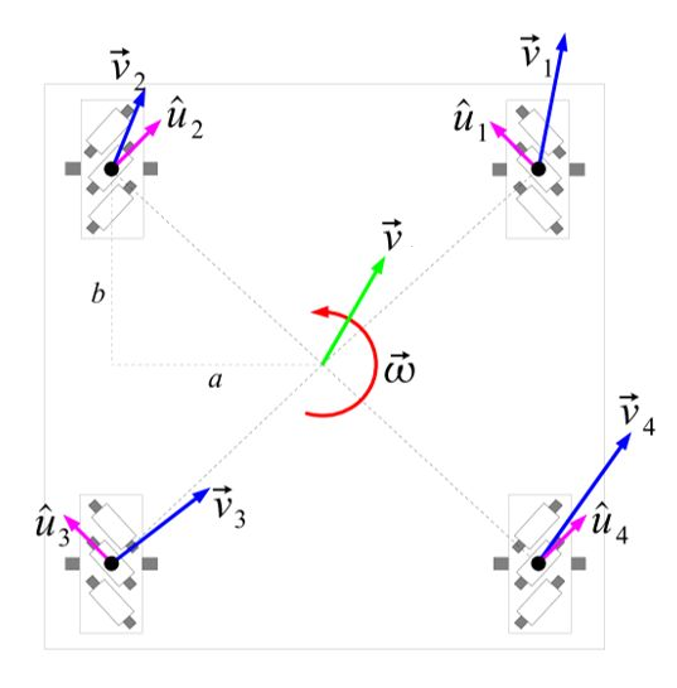
O-长方形麦克纳姆轮底盘的运动学模型如下所示：
$$\left[\begin{array}{c}{v}_{\omega 1}\\ v_{\omega 2}\\ v_{\omega 3}\\ v_{\omega 4}\end{array}\right]=\left[\begin{array}{ccc}-1& 1& a+b\\ 1& 1& -(a+b)\\ -1& 1& -(a+b)\\ 1& 1& (a+b)\end{array}\right]\left[\begin{array}{c}{v}_x\\ v_y\\ \omega \end{array}\right]$$

最后

以上就是酷炫花卷为你收集整理的里程计模型（3）：麦克纳姆轮底盘麦克纳姆轮底盘运动学模型的全部内容，希望文章能够帮你解决里程计模型（3）：麦克纳姆轮底盘麦克纳姆轮底盘运动学模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。