《Show, Attend and Tell: Neural Image Caption Generation with Visual Attention》论文阅读（详细）

参考资料：

[1502.03044v3] Show, Attend and Tell: Neural Image Caption Generation with Visual Attention (arxiv.org)

(PDF) Show, Attend and Tell: Neural Image Caption Generation with Visual Attention (researchgate.net)

sgrvinod/a-PyTorch-Tutorial-to-Image-Captioning: Show, Attend, and Tell | a PyTorch Tutorial to Image Captioning (github.com)

danielajisafe/Image-Captioning-Model (github.com)

贡献：

1、提出一种框架下的两种基于注意力的图像字幕生成方法：

​ a、一种可以通过标准反向传播可训练的“软”确定性的注意力；

​ b、一种可以通过最大化近似可变的下界或者REINFORCE的可训练的“硬”随机注意力机制；

2、将注意力可视化表示；

3、在三个数据集Flickr8k、Flickr30k、MS COCO达到最好结果；

模型：

模型的总体结构：

由卷积神经网络提取图片特征，然后由带注意力机制的循环神经网络一个单词接着一个单词生成。

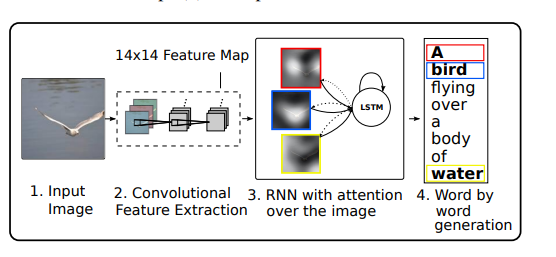
两种注意力结构：

硬注意力和软注意力的区别：

1、硬注意力得到的是类似于one-hot向量的权值。而软注意力得到的是softmax的输出权重值。随机硬注意力需要做Multinoulli的假设，也就是说只有一个等于1（事件发生），其余的都等于0（事件不发生）。

2、硬注意力的随机是因为使用Monte Carlo采样的方式求解，而软注意力的确定是因为使用期望的方式求解${\hat{z}}_t$。

1、随机硬注意力：

$$\begin{gathered} p(s_{t,i}=1|s_{j<t},aa)={\alpha }_{t,i} \\ {\hat{z}}_t=\sum _i{s}_{t,i}{aa}_i. \end{gathered}$$
公式的$s_t$指的是模型注意到的第t个词的位置。$s_{t,i}$指的是one-hot变量，当图片中的第$i$个位置被用来提取视觉特征则置1。

2、确定软注意力：

学习随机软注意力需要每次对注意力位置$s_t$进行采样，软注意力直接取上下⽂向量${\hat{z}}_t$的期望，是平滑和可微的:
$$E_{p(s_t|a)}[{\hat{z}\hat{z}}_t]=\sum _{i=1}^L{\alpha }_{t,i}{aa}_i$$
并且使用softmax进行归一化。将第 k 个单词预测的 softmax 的归⼀化加权⼏何平均 值（NWGM）写为：
$$NWGM[p(y_t=k|aa]=\frac{exp(E_{p(s_t|a)}[n_{t,k}])}{{\sum }_{j}exp(E_{p(s_t|a)}[n_{t,j}])}$$

将注意力嵌入到decoder中：

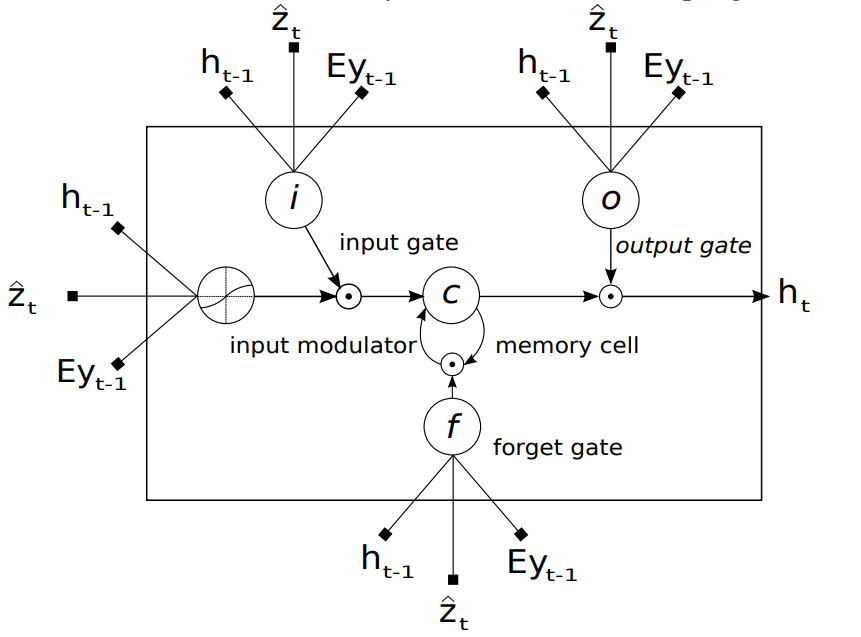
如图所示，将注意力结合LSTM得到decoder。图中的$\widehat{z_t}$由注意力机制$f_{att}$作用在图片块上生成：
$$\begin{array}{rl}{e}_{ti}& =f_{att}({aa}_i,h_{t-1})\\ a_{ti}& =\frac{exp(e_{ti})}{{\sum }_{k=1}^{L}exp(e_{tk})}\\ {\hat{z}}_t& =\varphi ({aa}_i,{\alpha }_i)\end{array}$$

注：多项式分布：多项式分布是二项式分布的推广。二项式做n次伯努利实验，规定了每次试验的结果只有两个。如果现在还是做n次试验，只不过每次试验的结果可以有m个，且m个结果发生的概率互斥且和为1，则发生其中一个结果X次的概率就是多项分布。概率密度函数是：
$$P(X_1=k_1,X_2=k_2,\cdots ,X_n=k_n)=\frac{n!}{(k_1!)(k_2!)\cdots (k_n!)}\prod _{i=1}^n(p_{k_i})$$

最后

以上就是丰富魔镜为你收集整理的《Show, Attend and Tell: Neural Image Caption Generation with Visual Attention》论文阅读（详细）的全部内容，希望文章能够帮你解决《Show, Attend and Tell: Neural Image Caption Generation with Visual Attention》论文阅读（详细）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。