概述
堆的定义
堆排序是一种树形结构选择排序方法，其特点是：在排序过程中，将序列视为一颗完全二叉树的顺序存储结构，利用完全二叉树中双亲结点和孩子结点之间的关系，在当前无序区间中选择关键字最大(或最小)的元素。堆的定义如下：
n 个关键字序列 L[1,2,3...n] 称为堆，当且仅当该序列满足：
① L(i) <= L(2i) 且 L(i) <= L(2i+1) ② L(i) >= L(2i) 且 L(i) >= L(2i+1) (1 <= i <= ⎿n/2⏌)
满足第一种情况的堆称为小根堆(或小顶堆)，满足第二种情况的堆称为大根堆(大顶堆)。在大根堆中，最大的元素存放在根结点中。对其任一非根结点，它的值小于等于其父亲结点的值。小根堆的定义刚好相反，根结点是最小元素。建立一个堆有两种方法，很多书籍把这两种方法称为向上调整和向下调整：
向下调整是让调整的结点与其孩子结点进行比较。
向上调整是让调整的结点与其父亲结点进行比较。
向上调整
向上调整需要从根结点开始建堆(以小根堆为例)，基本思路：每添加一个元素，将该元素与其父结点进行比较，若新增结点小于父结点，则交换两个结点的值，然后继续与上一级的父结点进行比较。停止向上调整的条件是该结点大于父结点的值。现有序列 list [ ] = {87, 45, 78, 32, 17, 65, 53, 9} 分别用向上调整和向下调整进行建堆，看看这两种方法有什么区别。
向上调整建堆的过程：
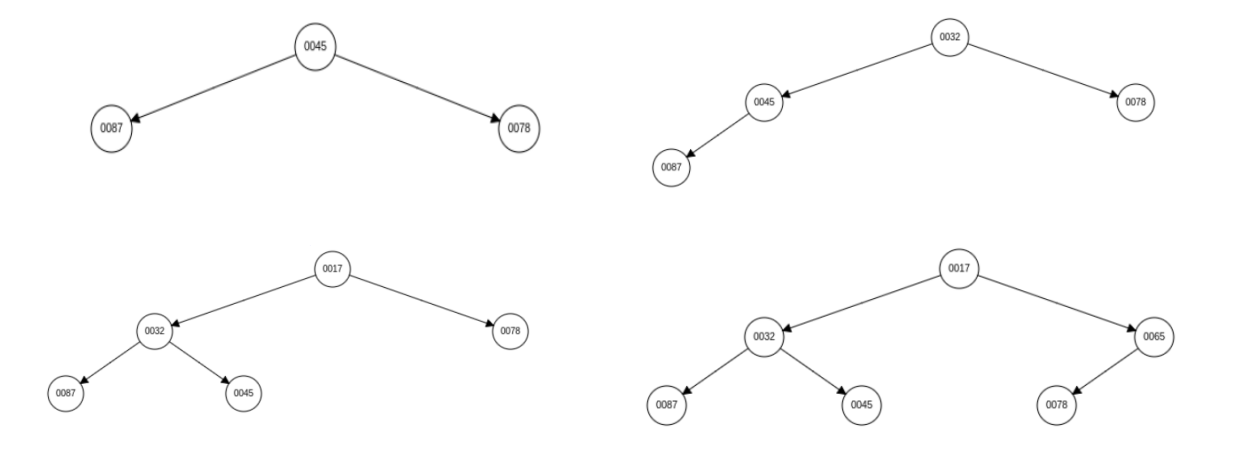
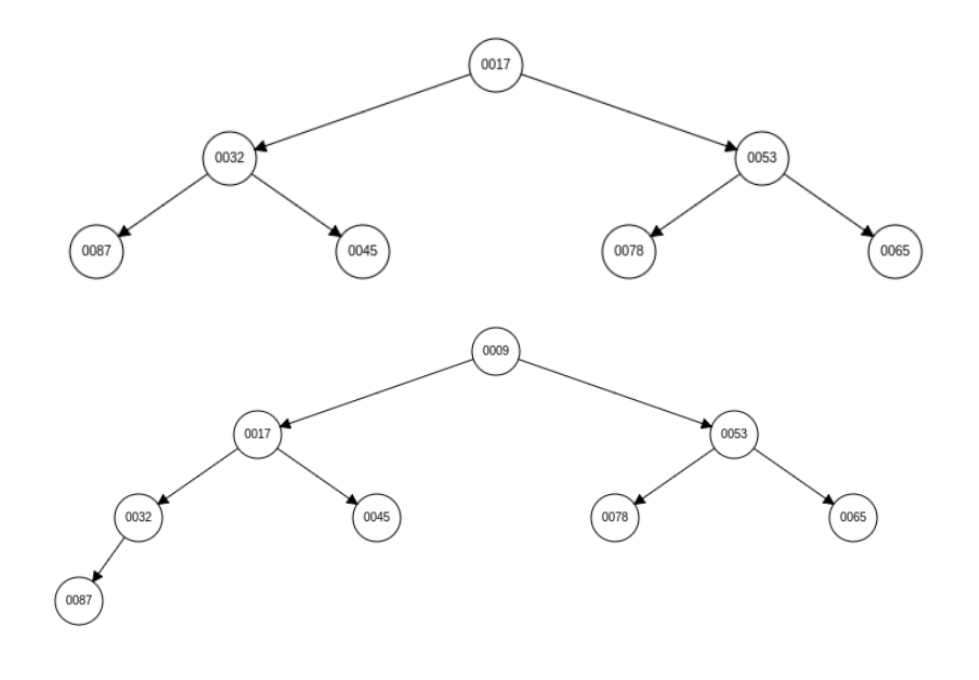
添加元素 9 的向上调整 gif：
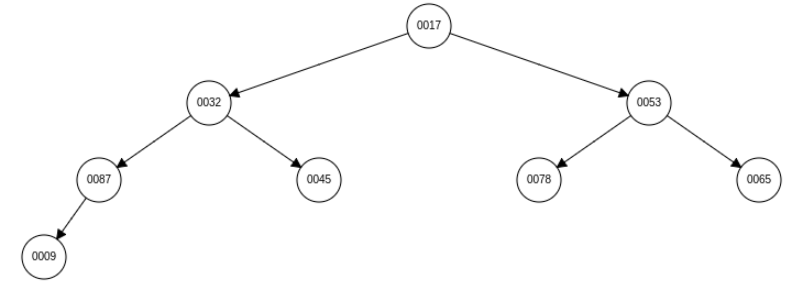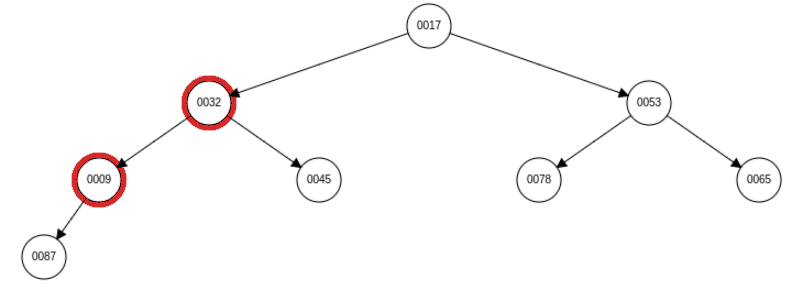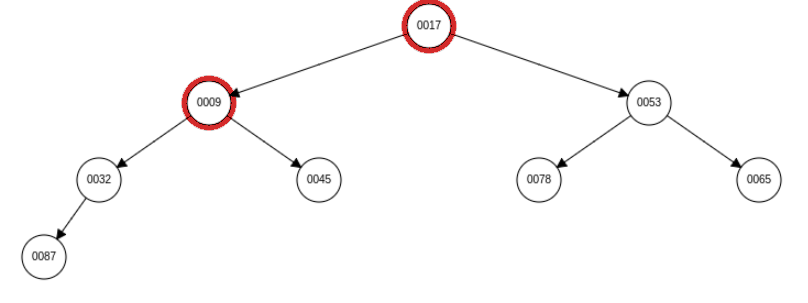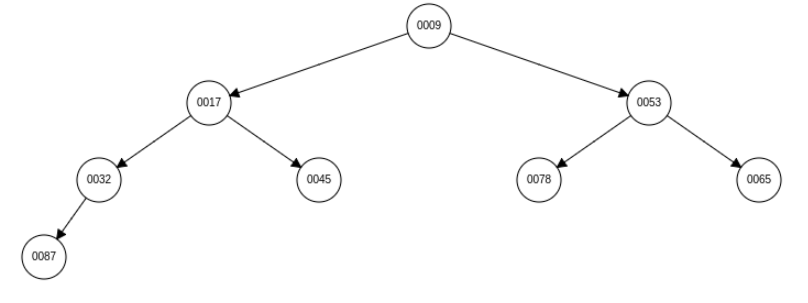
向上调整代码：
void AdjustUp(int a[],int size)
{ //size是数组目前的大小
int temp,flag=0;
if(size==1)
return; //此时是堆顶，不需要上调
while(size!=1 && flag==0)
{
if(a[size] < a[size/2]) //与父结点进行对比
{
temp = a[size];
a[size] = a[size/2];
a[size/2] = temp;
}
else
{
flag = 1;
}
size = size/2; //更新编号i为它父结点的编号。
}
}
void AdjustUp1(int a[], int k)
{//参数k为向上调整的结点，也是堆的元素个数
if(k == 1)
return;
a[0] = a[k];
int i = k/2;
while(i > 0 && a[i] > a[0]) //若结点值小于父结点，则将父结点向下调
{
a[k] = a[i]; //父节点向下调
k = i;
i = k/2; //继续向上比较
}
a[k] = a[0];
}
向下调整
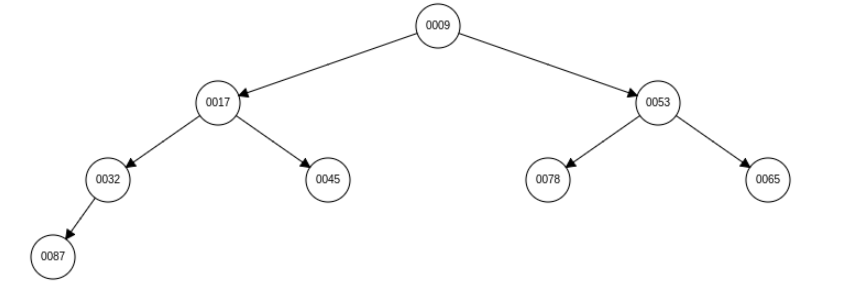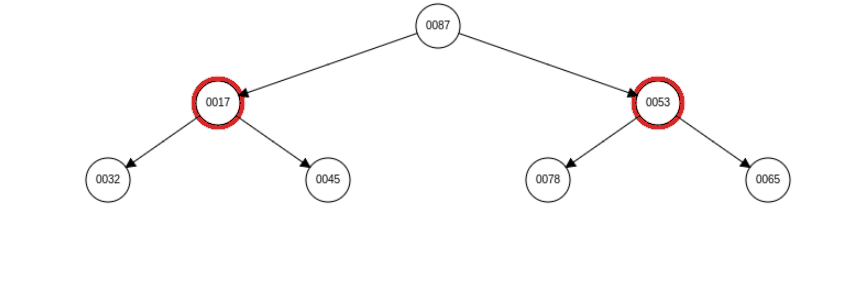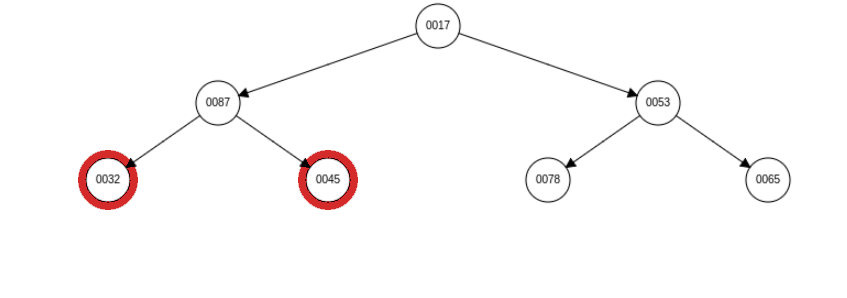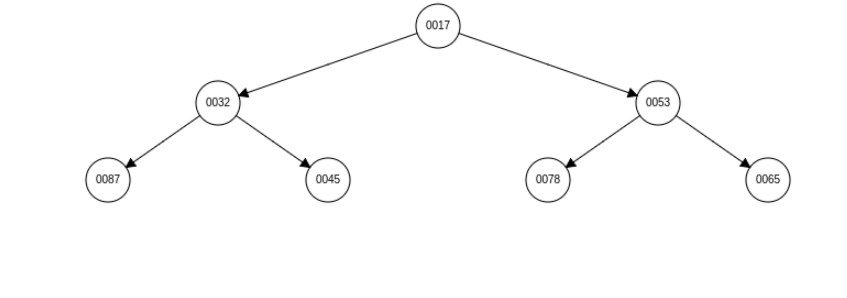
向下调整建堆是一个反复筛查的过程。n 个结点的完全二叉树，最后一个结点是第⎿n/2⏌个结点的孩子(完全二叉树的性质)。对第⎿n/2⏌个结点为根的子树筛查(对于小根堆，若结点的关键字大于左右孩子中关键字较小者，则交换)，使该子树成为堆。之后向前依次对各结点(⎿n/2⏌-1 ～ 1)为根的子树进行筛选，看该结点值是否小于其左右子结点的值，若不小于，则将左右子结点中的较小值与之交换，交换后可能会破坏下一级的堆，于是继续采取上述方法构造下一级的堆，直到以该结点为根的子树构成堆为止。反复利用上述调整方法建堆，直到根结点。根据原始数据建立的树形结构如下：
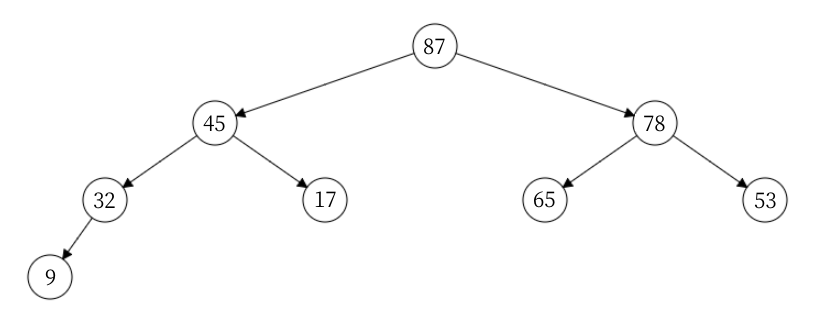
根据向下调整的思路，从第 4 个结点开始进行筛查建立小根堆：
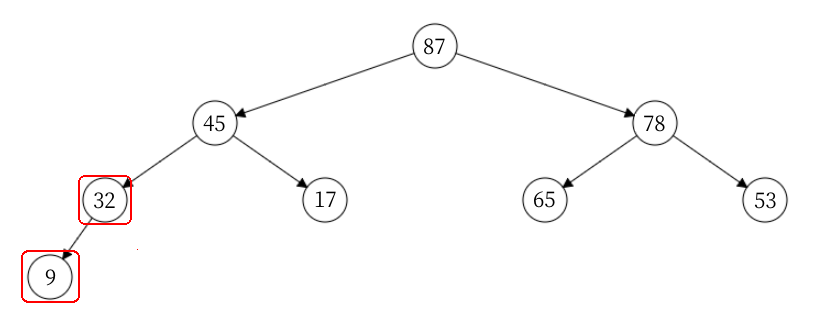
向下调调整思路：将该结点与其孩子结点进行比较，选取其中最小进行交换，若该节点本身就是最小的结点，则不需要进行交换操作。如上图，需要将 9 和 32 进行交换。然后对第 3 个结点进行调整，该过程较为简单，所以省略。接下来展示第 2 个结点的调整情况。
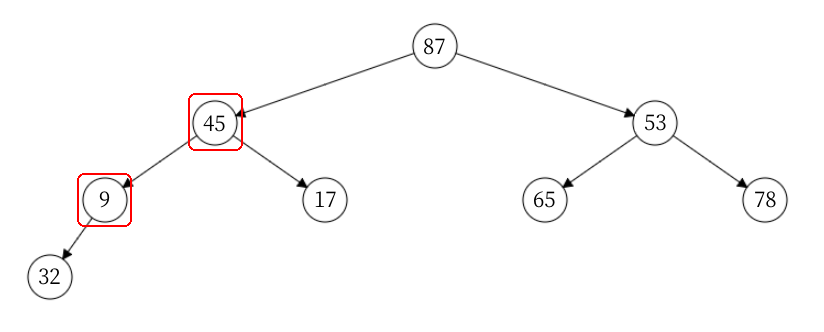
对第 2 个结点进行调整时，需要交换 9 和 45。但是交换后发现 32 比 45 要小，所以还需要进行一次交换操作。该过程告诉我们，在交换父子结点后，子结点的堆属性可能被破坏，所以要对子结点进行调整(直至子结点为叶子结点为止)。以下是第 2 个结点最终的调整情况：
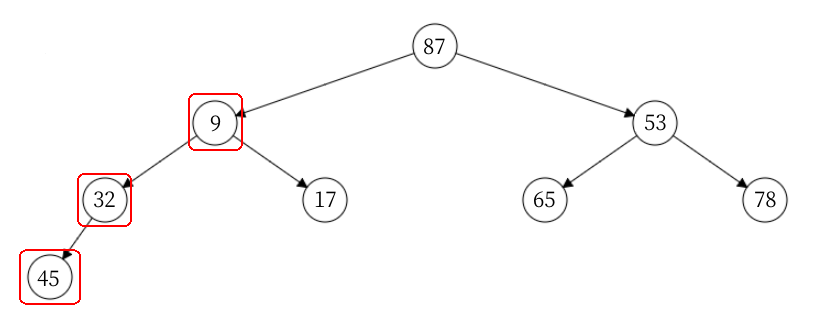
向下调整的最终形态：
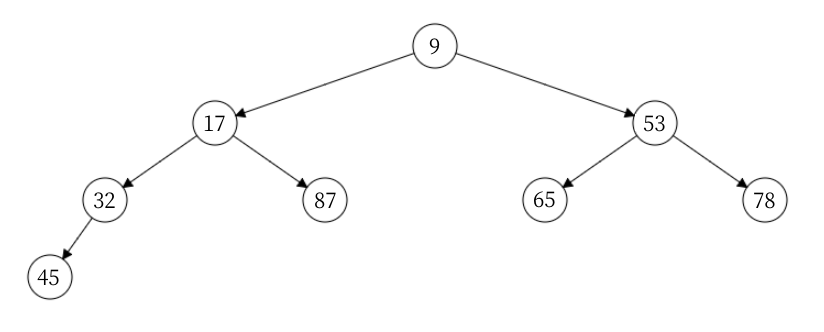
向下调整 gif：
向下调整代码：
void heap_ajust_min(int *b, int i, int size) //a为数组，size为堆的大小
{
int lchild = 2*i; //i的左孩子节点序号
int rchild = 2*i +1; //i的右孩子节点序号
int min = i; //记录根和左右子树中最小的数的下标
int temp;
if(i <= size/2) //调整不需要从叶结点开始
{
if(lchild<=size && b[lchild]<b[min])
{
min = lchild;
}
if(rchild<=size && b[rchild]<b[min])
{
min = rchild;
} //两个if语句寻找三个结点中最小的数
if(min != i) //如果min不等于i，说明最小的值在左右子树中
{
temp = b[i]; //交换a[i]和a[min]的值
b[i] = b[min];
b[min] = temp;
heap_ajust_min(b, min, size); //被交换的子树可能不满足堆的定义，需要对被交换的子树重新调整
}
}
}
void build_heap_min(int *b, int size) //建立小根堆
{
int i;
for(i = size/2; i >= 1; i--) //非叶子节点最大序号值为size/2，从这个结点开始调整
{ //注意for中的循环条件(i = size/2; i >= 1; i--)
heap_ajust_min(b, i, size);
}
}向下调整的时间与树的高度有关，为 O(h)。建堆过程中每次向下调整时，大部分结点的高度都比较小。我们很容易会发现向上调整和向下调整的最终结果有所不同，但都满足了小根堆的性质。向上调整和向下调整都能够完成建立堆的工作。区别在于，使用向上调整建堆需要从第一个元素开始，过程相当于每次插入一个元素，然后再进行向上调整的工作。向下调整充分的利用了完全二叉树的性质，从⎿n/2⏌结点到根结点逐一筛查。它们的具体操作如下：
for(k = 1; k < size ; ++k) //向上调整建堆
{
AdjustUp(b, k);
}
for(i = size/2; i >= 1; i--) //向下调整建堆
{
heap_ajust_min(b, i, size);
}
堆排序
应用堆进行排序的思路很简单：首先将存放在 L[1,2,3...n] 中的 n 个元素建成初始堆，由于堆本身的特点，堆顶元素就是最值。输出堆顶元素后，通常将堆底元素送入堆顶，此时根结点不满足堆的性质，经过向下调整后使其恢复堆的性质，再输出堆顶元素。重复操作，直至最后一个元素为止。
堆排序代码：
void heap_sort_min(int *a, int size)
{
int i;
int temp;
for(i = size; i >= 1; i--)
{
temp = a[1];
a[1] = a[i];
a[i] = temp; //交换堆顶和最后一个元素
heap_ajust_min(a, 1, i-1); //再一次调整堆顶节点成为小顶堆
}
} 利用上述小根堆代码完成排序，会发现序列是倒序的，这是因为排序过程是从后往前不断调整小根堆的结果。如果想要获得升序序列，需要使用大根堆进行排序。
堆支持删除和插入操作，删除元素时，需要将最后一个元素放到堆顶，然后使用向下调整，使堆保持堆的特性。对堆进行插入操作时，先将新结点放在堆的末端，再对这个新结点进行向上调整操作。注意：插入元素时(小根堆为例)，只需要调用一次向上调整函数便能恢复堆的属性。因为在插入之前，堆本身是完整的。此时若插入元素小于父结点的值，那么只需要交换两个结点而不需要考虑别的情况。这是因为之前满足堆性质，而插入了一个更小的值，交换后堆属性不变。具体可以看添加 9 的时候的 gif。可以根据需求，将向上调整和向下调整搭配着使用。例如：小根堆删除元素后使用向下调整恢复堆的性质。
完整代码：
#include<stdio.h>
#include<math.h>
void heap_ajust_min(int *b, int i, int size) /*a为堆存储数组，size为堆的大小*/
{
int lchild = 2*i; //i的左孩子节点序号
int rchild = 2*i +1; //i的右孩子节点序号
int min = i; /*存放三个顶点中最大的数的下标*/
int temp;
if(i <= size/2) //假设i是叶节点就不用进行调整
{
if(lchild<=size && b[lchild]<b[min])
{
min = lchild;
}
if(rchild<=size && b[rchild]<b[min])
{
min = rchild;
}
if(min != i)
{
temp = b[i]; /*交换a[i]和a[max]的值*/
b[i] = b[min];
b[min] = temp;
heap_ajust_min(b, min, size); /*被交换的位置曾经是大根堆，如今可能不是大根堆
所以须要又一次调整使其成为大根堆结构*/
}
}
}
void build_bheap_min(int *b, int size) //建立小堆
{
int i;
for(i=size/2; i >= 1; i--) //非叶节点最大序号值为size/2
{
heap_ajust_min(b, i, size);
}
}
void heap_sort_min(int *a, int size)
{
int i;
int temp;
for(i = size; i >= 1; i--)
{
temp = a[1];
a[1] = a[i];
a[i] = temp; //交换堆顶和最后一个元素
heap_ajust_min(a, 1, i-1); //再一次调整堆顶节点成为小顶堆
}
}
void AdjustUp(int a[],int size)
{
int temp,flag=0;
int k;
if(size==1)
return;//此时是堆顶，不需要上调
while(size!=1 && flag==0)
{
if(a[size] < a[size/2])
{
temp = a[size];
a[size] = a[size/2];
a[size/2] = temp;
}
else
{
flag = 1;
}
size = size/2;//更新编号i为它父结点的编号。
}
}
void AdjustUp1(int a[], int k)
{//参数k为向上调整的结点，也是堆的元素个数
if(k == 1)
return;
a[0] = a[k];
int i = k/2;
while(i > 0 && a[i] > a[0]) //若结点值小于父结点，则将父结点向下调
{
a[k] = a[i]; //父节点向下调
k = i;
i = k/2; //继续向上比较
}
a[k] = a[0];
}
int main(int argc, char *argv[])
{
int i,j,k;
int count=1;
int a[]={0, 87, 45, 78, 32, 17, 65, 53, 9};
int b[]={0, 87, 45, 78, 32, 17, 65, 53, 9};
int size = sizeof(a)/sizeof(int) -1;
build_bheap_min(a, size);
printf("向下调整建立小顶堆:n");
count=1;
for(i=0;i<=4;i++)
{
for(j=0;j<pow(2,i);j++)
{
if(count<=size)
{
printf("%d ",a[count++]);
}else{
break;
}
}
printf("n");
}
for(k = 1; k < 9 ; ++k)
{
AdjustUp(b, k);
}
printf("向上调整小顶堆:n");
count=1;
for(i=0;i<=4;i++)
{
for(j=0;j<pow(2,i);j++)
{
if(count<=size)
{
printf("%d ",b[count++]);
}else{
break;
}
}
printf("n");
}
return 0;
}
最后
以上就是独特纸飞机为你收集整理的通俗易懂的讲解堆排序(含Gif图)的全部内容，希望文章能够帮你解决通俗易懂的讲解堆排序(含Gif图)所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复