堆排序的时间复杂度O(N*logN),额外空间复杂度O(1)，是一个不稳定性的排序

目录

堆排序介绍

堆数组 顺序表结构

对应的堆 逻辑结构 

思考一????：如何将无序的数组转为大根堆或者小根堆呢？

思考二????：如何完成最终顺序结构排序？

代码实现

复杂度分析

堆排序介绍

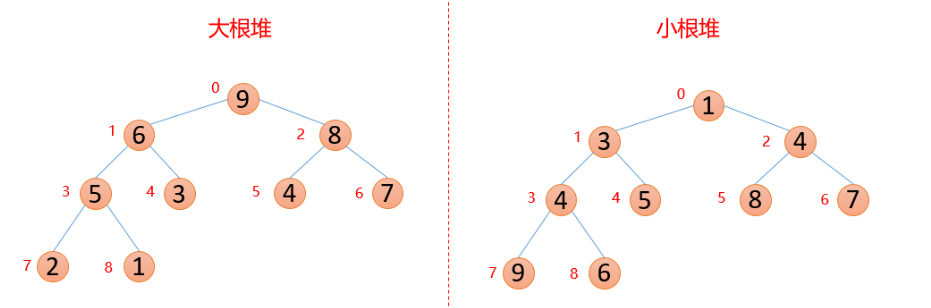
n个关键字序列List[1,2,3...N]称为堆(后面简写为L)，物理结构可以是顺序存储也可以是链式存储(在例子中我们统一使用顺序存储结构)，逻辑结构则是完全二叉树(要具有抽象思想),堆又分为大根堆和小根堆。

当L(i) <= L(2i + 1)且L(i) <= L(2i + 2),则称为 小根堆

当L(i) >= L(2i + 1)且L(i) >= L(2i + 2),则称为 大根堆（本质就是小根堆的反转）

这里看个例子如下：

堆数组 顺序表结构

对应的堆 逻辑结构 

 本文将要讲解堆排序，那么对于一个无序数组我们应该如何得到有序的输出呢？

（1）先将无序的数组调整成堆结构（升序用大根堆，降序就用小根堆），此时，整个数组的最大(小)值就是堆结构的顶端

（2）.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

（3）将剩余的n-1个数再调整成大根堆，如何调整？只需要从顶端调整一次就OK。

重复（2）（3）步骤（注意：每次都需要减1）

是不是很抽象，是不是感觉似懂非懂，问题不大，我刚开始的时候也这样，接下来我将通过图的方式让你加深理解。

思考一????：如何将无序的数组转为大根堆或者小根堆呢？

将物理结构转为抽象的树，然后对所有具有双亲节点含义 编号从大到小（[n-1]/2）做如下调整：(注：这里注意下，n 看你如何定义，如果是根据数组长度的话，那么就是直接n/2,那个位子开始，因此这里需要灵活的变通，但是最终是获取到开始调整的位子)

①若孩子节点皆 小于父节点，则该节点的调整结束

②若存在孩子节点大于双亲节点，则将最大的孩子节点与父节点交换，并对该孩子节点进行① ②操作，直到出现①或到叶节点为止。

例子：根据数组抽象出对应的逻辑结构树，现在是无序的

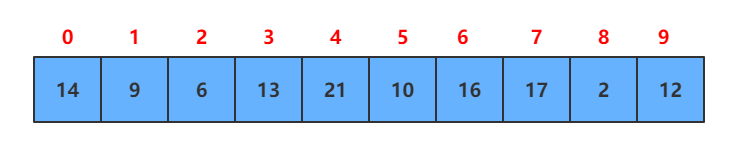
是不是感觉很抽象，问题不大，来个图解：

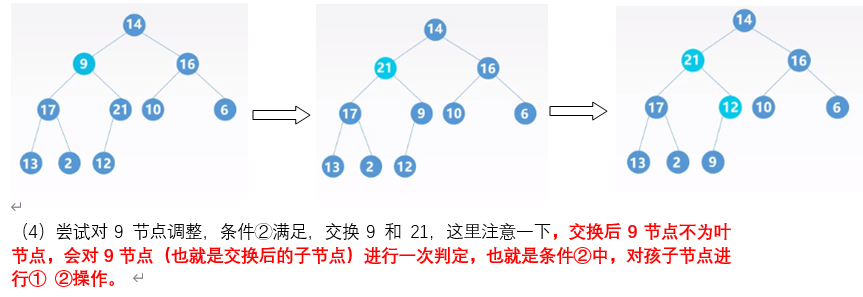
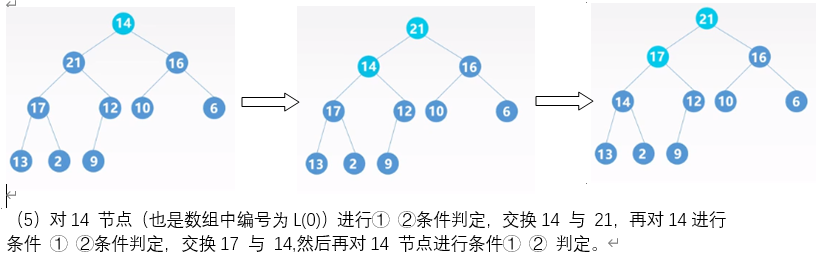
通过以上步骤就完成了从无序数组，调整为大根堆，对应如下的顺序表数据结构。

完成了第（1）步，构造成了一个大根堆，但是我们排序并没有完成，其实也可以说完成了，因为从大根堆的角度来说已经排序好了，但是从顺序数据结构来说，仍然是无序的。

思考二????：如何完成最终顺序结构排序？

接下来我们将进行第（2）（3）步的操作，还是再看一遍抽象的逻辑结构树

 开始进行输出，进行一次（2）（3），注意顶端的数与末尾的数(最后一个未排序的数)交换。

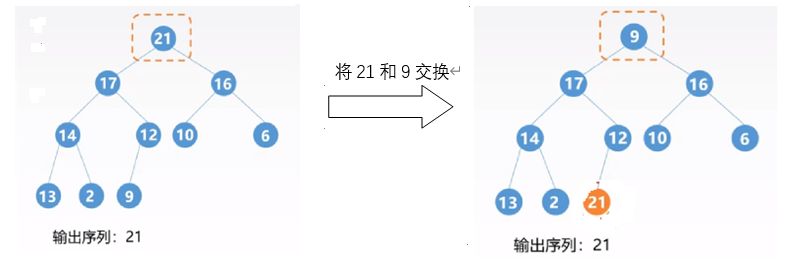
此时结构已经不是一个大根堆了，需要再调整为大根堆（只需要从顶点9调整一次就OK），再将顶端17与为排序的最末端端（也就是每次n-1位）调换

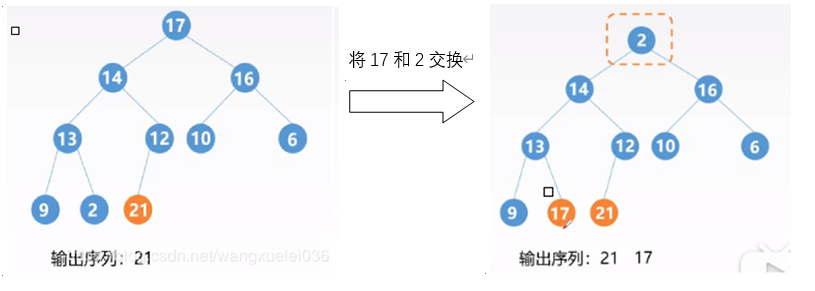
不断的重复就能完成排序，树的逻辑结构比较清楚了，那么顺序表数据结构也要了解下（省略了第一步将无序数组构建为大根堆的过程）：

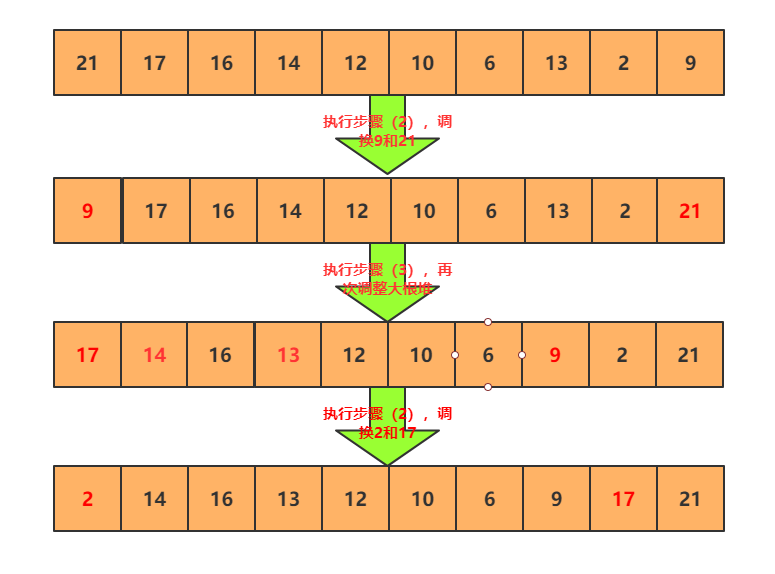
上面例子重复了两次，我们发现 17 和 21 已经就位了，那么不对的重复（2）（3）就能完成我们的数组排序。 如果有时间，建议剩下的自己尝试调整下。

代码实现

public class HeapSort {
 
	public static void heapSort(int[] arr) {
		if (arr == null || arr.length == 0) {
			return;
		}
		int len = arr.length;
		// 构建大顶堆，这里其实就是把待排序序列，变成一个大顶堆结构的数组
		buildMaxHeap(arr, len);
 
		// 交换堆顶和当前末尾的节点，重置大顶堆
		for (int i = len - 1; i > 0; i--) {
			swap(arr, 0, i);
			len--;
			heapify(arr, 0, len);
		}
	}
 
	private static void buildMaxHeap(int[] arr, int len) {
		// 从最后一个非叶节点开始向前遍历，调整节点性质，使之成为大顶堆
		for (int i = (int)Math.floor(len / 2) - 1; i >= 0; i--) {
			heapify(arr, i, len);
		}
	}
 
	private static void heapify(int[] arr, int i, int len) {
		// 先根据堆性质，找出它左右节点的索引
		int left = 2 * i + 1;
		int right = 2 * i + 2;
		// 默认当前节点（父节点）是最大值。
		int largestIndex = i;
		if (left < len && arr[left] > arr[largestIndex]) {
			// 如果有左节点，并且左节点的值更大，更新最大值的索引
			largestIndex = left;
		}
		if (right < len && arr[right] > arr[largestIndex]) {
			// 如果有右节点，并且右节点的值更大，更新最大值的索引
			largestIndex = right;
		}
 
		if (largestIndex != i) {
			// 如果最大值不是当前非叶子节点的值，那么就把当前节点和最大值的子节点值互换
			swap(arr, i, largestIndex);
			// 因为互换之后，子节点的值变了，如果该子节点也有自己的子节点，仍需要再次调整。
			heapify(arr, largestIndex, len);
		}
	}
 
	private static void swap (int[] arr, int i, int j) {
		int temp = arr[i];
		arr[i] = arr[j];
		arr[j] = temp;
	}
}

复杂度分析

因为堆排序无关乎初始序列是否已经排序已经排序的状态，始终有两部分过程，构建初始的大顶堆的过程时间复杂度为O(n)，交换及重建大顶堆的过程中，需要交换n-1次，重建大顶堆的过程根据完全二叉树的性质，[log2(n-1),log2(n-2)...1]逐步递减，近似为nlogn。所以它最好和最坏的情况时间复杂度都是O(nlogn)，空间复杂度O(1)。 

参考：

https://blog.csdn.net/u010452388/article/details/81283998

最后

以上就是高高巨人为你收集整理的堆排序算法（图解详细流程）无序 -》 堆 -》 有序堆排序介绍思考一????：如何将无序的数组转为大根堆或者小根堆呢？思考二????：如何完成最终顺序结构排序？代码实现复杂度分析参考：的全部内容，希望文章能够帮你解决堆排序算法（图解详细流程）无序 -》 堆 -》 有序堆排序介绍思考一????：如何将无序的数组转为大根堆或者小根堆呢？思考二????：如何完成最终顺序结构排序？代码实现复杂度分析参考：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。