神经网络算法---手写数字体识别

神经网络的背景

1，1980年backpropagation是神经网络算法最著名的算法，以人脑中的神经网络为启发。

多层向前神经网络

• backpropagation被使用在多层向前神经网络上
• 多层向前神经网络由一下3个部分组成：输入层，隐藏层，输出层
• 
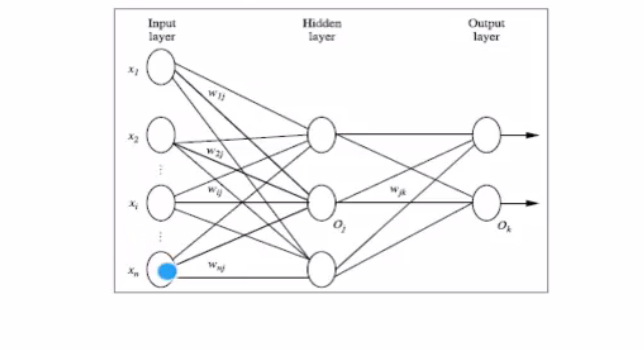
• 每层由单元组成
• 输入层由训练集的实例特征向量传入
• 经过连接结点的权重传入下一层，一层的输出是下一层的输入
• 每个单元可以被称为神经结点，
• 隐藏层的个数可以是任意的，输入层由一层，输出层一层
• 上图是两层的神经网络（输出层不算）
• 一层中加权的求和，然后根据非线性方程转化成为输出
• 理论上，如果有足够多的隐藏层和足够大的训练集，可以模拟任何方程。（功能强大）（设多少层，每层多少个）

设计神经网络结构

• 使用神经网络训练数据之前，必须确定神经网络的层数，以及每层单元的个数
• 特征向量在被传入输入层时常常被先标准化到0到1之间（目的是加速学习过程）
• 离散型变量可以被编码成每一个输入单元对应特征值可能的赋值
• 神经网络既可以解决分类问题，又能解决回归问题，没有明确的规则来设计最好有多少个隐藏层，根据实验测试和误差，以及准确度来实验并且改进

交叉验方法

将数据分成k份，每次取其中一份当作测试集，其余的当层训练集，循环k次，再将准确度取平均。

Backpropagation 算法

• 通过迭代性来处理训练集中的实例
• 对比经过神经网络后的输入层的预测值和真实值之间的差距
• 反方向（从输出层-》隐藏层-》输入层）来最小化误差来更新每个连接的权重

激活函数

• 非线性转化的过程用来做激活函数。
• 双曲函数和逻辑函数都能做为激活函数。
• sigmoid函数将y值在（0，1）之间变化的函数。

手写数字例子

首先构建神经网络

 import numpy as np


def tanh(x):
    return np.tanh(x)


def tanh_deriv(x):
    return 1.0 - np.tanh(x) * np.tanh(x)


def logistic(x):
    return 1 / (1 + np.exp(-x))


def logistic_derivative(x):
    return logistic(x) * (1 - logistic(x))


class NeuralNetwork:
    def __init__(self, layers, activation='tanh'):
        # 根据类实例化一个函数，_init_代表的是构造函数
        # self相当于java中的this
        """
        :param layers:一个列表，包含了每层神经网络中有几个神经元，至少有两层，输入层不算作
                [, , ,]中每个值代表了每层的神经元个数
        :param activation：激活函数可以使用tanh 和 logistics，不指明的情况下就是tanh函数
        """
        if activation == 'logistic':
            self.activation = logistic
            self.activation_deriv = logistic_derivative
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_deriv = tanh_deriv
        # 初始化weights,
        self.weights = []
        # len(layers)layer是一个list[10,10,3]，则len(layer)=3
        # 除了输出层都要赋予一个随机产生的权重
        for i in range(1, len(layers) - 1):
            # np.random.random为nunpy随机产生的数
            # 实际是以第二层开始，前后都连线赋予权重，权重位于[-0.25,0.25]之间
            self.weights.append((2 * np.random.random((layers[i - 1] + 1, layers[i] + 1)) - 1) * 0.25)
            self.weights.append((2 * np.random.random((layers[i] + 1, layers[i + 1])) - 1) * 0.25)

    # 定义一个方法，训练神经网络
    def fit(self, X, y, learning_rate=0.2, epochs=10000):
        # X：数据集,确认是二维，每行是一个实例，每个实例有一些特征值
        X = np.atleast_2d(X)
        # np.ones初始化一个矩阵，传入两个参数全是1
        # X.shape返回的是一个list[行数，列数]
        # X.shape[0]返回的是行，X.shape[1]+1：比X多1，对bias进行赋值为1
        temp = np.ones([X.shape[0], X.shape[1] + 1])
        # “ ：”取所有的行
        # “0：-1”从第一列到倒数第二列，-1代表的是最后一列
        temp[:, 0:-1] = X
        X = temp
        # y：classlabel，函数的分类标记
        y = np.array(y)
        # K代表的是第几轮循环
        for k in range(epochs):
            # 从0到X.shape[0]随机抽取一行做实例
            i = np.random.randint(X.shape[0])
            a = [X[i]]

            # 正向更新权重    ，len(self.weights)等于神经网络层数
            for l in range(len(self.weights)):
                # np.dot代表两参数的内积，x.dot(y) 等价于 np.dot(x,y)
                # 即a与weights内积，之后放入非线性转化function求下一层
                # a输入层，append不断增长，完成所有正向的更新
                a.append(self.activation(np.dot(a[l], self.weights[l])))
            # 计算错误率，y[i]真实标记   ，a[-1]预测的classlable
            error = y[i] - a[-1]
            # 计算输出层的误差，根据最后一层当前神经元的值，反向更新
            deltas = [error * self.activation_deriv(a[-1])]

            # 反向更新
            # len(a)所有神经元的层数，不能算第一场和最后一层
            # 从最后一层到第0层，每次-1
            for l in range(len(a) - 2, 0, -1):
                #
                deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_deriv(a[l]))
            # reverse将deltas的层数跌倒过来
            deltas.reverse()
            for i in range(len(self.weights)):
                #
                layer = np.atleast_2d(a[i])
                # delta代表的是权重更新
                delta = np.atleast_2d(deltas[i])
                # layer.T.dot(delta)误差和单元格的内积
                self.weights[i] += learning_rate * layer.T.dot(delta)

    def predict(self, x):
        x = np.array(x)
        temp = np.ones(x.shape[0] + 1)
        # 从0行到倒数第一行
        temp[0:-1] = x
        a = temp
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        return a
 

接着创建主函数

from main import NeuralNetwork
import numpy as np
#导入数据集的包
from sklearn.datasets import load_digits
#将数据分成数据集和训练集的包
from sklearn.model_selection import train_test_split
#二值化的函数
from sklearn.preprocessing import LabelBinarizer
from sklearn.metrics import confusion_matrix,classification_report
#下载包
digits = load_digits()
X = digits.data
y = digits.target
#简单的预处理，将x标准花为（0，1）之间
X -= X.min()
X /= X.max()


#实例化神经网络 每个图都是64个像素点，有64个维度，每个都是神经元，隐藏层100，输出层10（输入层和特征向量像素一样，输出层和要分成多少类一样。）
nn = NeuralNetwork([64,100,10],"logistic")
#将数据分为测试集，训练集和
X_train,X_test,y_train,y_test = train_test_split(X,y)
#将包转换成二维的数字类型，
label_train = LabelBinarizer().fit_transform(y_train)
label_test =  LabelBinarizer().fit_transform(y_test)
print("start fitting")
# 放入神经网络
nn.fit(X_train,label_train,epochs=3000)
predictions = []
for i in range(X_test.shape[0]):
    o = nn.predict(X_test[i])
    predictions.append(np.argmax(o))
    #confusion_matrix绘图的正确性， 对角线是真实值和预测值相同。对角线上的位置都是预测对了
print(confusion_matrix(y_test,predictions))
# 准确度
print(classification_report(y_test,predictions))
#precision 预测对的概率，recall：真实值是零的时候，预测为正确的该路

最后结果展示：

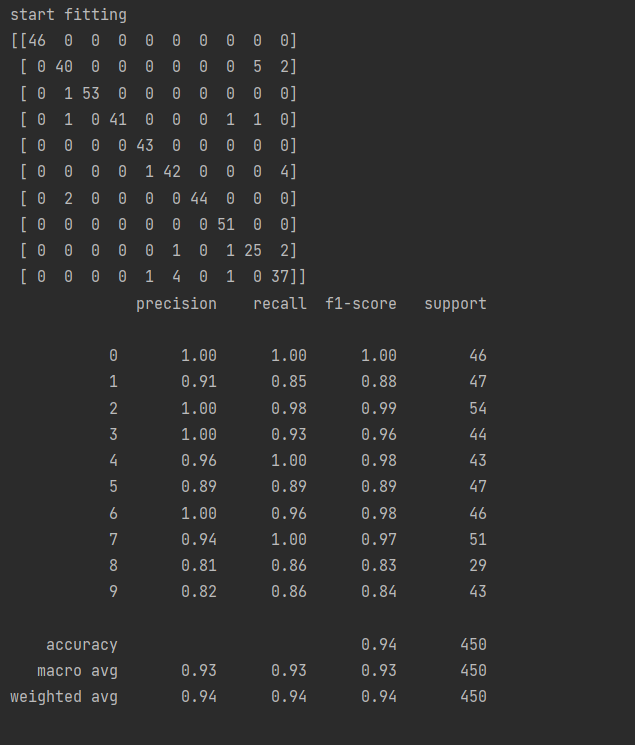
最后

以上就是细心冥王星为你收集整理的神经网络算法---手写数字体识别的全部内容，希望文章能够帮你解决神经网络算法---手写数字体识别所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。