pytorch基础操作(四)softmax回归手动实现以及pytorch的API实现

1、softmax解决多分类问题

假设每次输⼊是⼀个2 × 2的灰度图像。我们可以⽤⼀个标量表⽰每个像素值，每个图像对应四个特征x1, x2, x3, x4。此外，假设每个图像属于类别“猫”，“鸡”和“狗”中的⼀个。

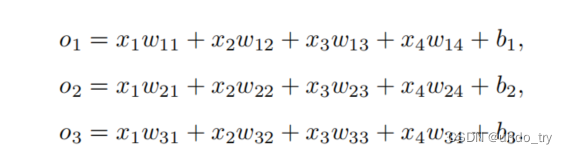
1、softmax公式

softmax函数能够将未规范化的预测变换为⾮负数并且总和为1，同时让模型保持可导的性质。为了完成这⼀⽬标，我们⾸先对每个未规范化的预测求幂，这样可以确保输出⾮负。为了确保最终输出的概率值总和为1，我们再让每个求幂后的结果除以它们的总和。
这⾥，对于所有的j总有0 ≤ yˆj ≤ 1。因此，yˆ可以视为⼀个正确的概率分布。softmax运算不会改变未规范化的预测o之间的⼤⼩次序，只会确定分配给每个类别的概率。

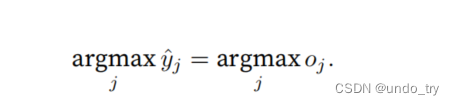
尽管softmax是⼀个⾮线性函数，但softmax回归的输出仍然由输⼊特征的仿射变换决定。因此，softmax回归是⼀个线性模型（linear model）。

2、loss函数(交叉熵损失)

用交叉熵损失函数来度量多分类预测的效果。

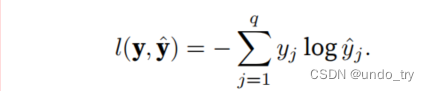
y是⼀个⻓度为q的独热编码向量，所以除了⼀个项以外的所有项j都消失了。

3、loss函数的梯度

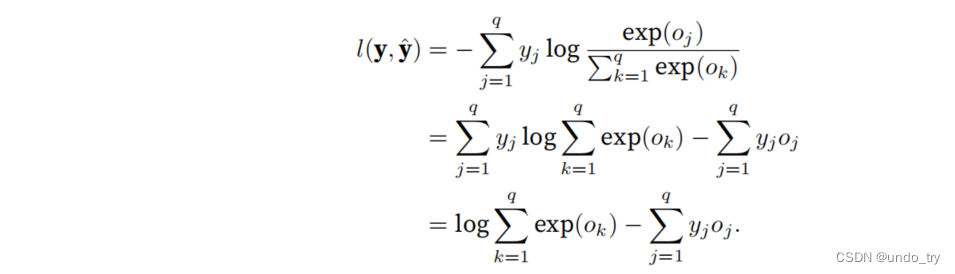
可以看出，梯度是观测值y和估计值yˆ之间的差异。

2、softmax回归的手动实现

1、读取服装分类数据集 Fashion-MNIST

# 通过框架中的内置函数将Fashion-MNIST数据集下载并读取到内存中
# Fashion-MNIST是⼀个服装分类数据集，由10个类别的图像组成
# Fashion-MNIST由10个类别的图像组成，每个类别由训练数据集（train dataset）中的6000张图像和测试数据集（test dataset）中的1000张图像组成。
# 因此，训练集和测试集分别包含60000和10000张图像。

'''
  1、读取服装分类数据集 Fashion-MNIST
'''
import torchvision
import torch
from torch.utils import data
from torchvision import transforms


def get_dataloader_workers():
    """使⽤4个进程来读取数据"""
    return 4



def get_mnist_data(batch_size, resize=None):
    trans = [transforms.ToTensor()]

    if resize:
        # 还接受⼀个可选参数resize，⽤来将图像⼤⼩调整为另⼀种形状
        trans.insert(0,transforms.Resize(resize))
    trans = transforms.Compose(trans)

    mnist_train = torchvision.datasets.FashionMNIST(
        root='../data',train=True,transform=trans,download=True
    )


    mnist_test = torchvision.datasets.FashionMNIST(
        root='../data',train=False,transform=trans,download=True
    )
    # 数据加载器每次都会读取⼀⼩批量数据，⼤⼩为batch_size。通过内置数据迭代器，我们可以随机打乱了所有样本，从⽽⽆偏⻅地读取⼩批量
    # 数据迭代器是获得更⾼性能的关键组件。依靠实现良好的数据迭代器，利⽤⾼性能计算来避免减慢训练过程。
    train_iter = data.DataLoader(mnist_train,batch_size=batch_size,shuffle=True,num_workers=get_dataloader_workers())
    test_iter = data.DataLoader(mnist_test,batch_size=batch_size,shuffle=True,num_workers=get_dataloader_workers())

    return (train_iter,test_iter)


batch_size = 256

train_iter,test_iter = get_mnist_data(batch_size)

2、初始化模型参数

'''
  2、初始化模型参数

  服装分类数据集中的每个样本都是28×28的图像，一共含有10个类别。

  我们将展平每个图像，把它们看作长度为784的向量，暂时把每个像素位置看作一个特征。

  softmax回归中，输出与类别一样多，因为数据集有10个类别，因此网络输出的纬度为10.

  因此，权重将构成⼀个784 × 10的矩阵，偏置将构成⼀个1 × 10的⾏向量。
  与线性回归⼀样，我们将使⽤正态分布初始化我们的权重W，偏置初始化为0。
'''

num_inputs = 784
num_outputs = 10


# 与线性回归⼀样，我们将使⽤正态分布初始化我们的权重W，偏置初始化为0。
W = torch.normal(
    0,
    0.01,
    size=(num_inputs, num_outputs),
    requires_grad=True
)
b = torch.zeros(num_outputs, requires_grad=True)

3、定义softmax操作

'''
  3、定义softmax操作
'''

# 回顾⼀下sum运算符如何沿着张量中的特定维度⼯作
X = torch.tensor([
    [1.0, 2.0, 3.0],
    [4.0, 5.0, 6.0]
])

# 给定⼀个矩阵X，我们可以对所有元素求和（默认情况下）。
# 也可以只求同⼀个轴上的元素，即同⼀列（轴0）或同⼀⾏（轴1）
# X是⼀个形状为(2, 3)的张量，我们对列进⾏求和，则结果将是⼀个具有形状(3,)的向量。
# 当调⽤sum运算符时，我们可以指定保持在原始张量的轴数，⽽不折叠求和的维度。这将产⽣⼀个具有形状(1, 3)的⼆维张量。
X.sum(), X.sum(0), X.sum(0,  keepdim=True), X.sum(1,  keepdim=True)

'''
实现softmax的三个步骤：
  1、对每个项求幂(exp)
  2、对每一行求和(小批量中每个样本是一行)，得到每个样本的规范化常数
  3、将每一行除以规范化常数，确保结果的和为1
'''
def softmax(X):
    # 1、对每个项求幂(exp)
    X_exp = torch.exp(X)
    # 2、对每一行求和(小批量中每个样本是一行)，得到每个样本的规范化常数
    partition = X_exp.sum(1, keepdim=True)

    # 3、将每一行除以规范化常数，确保结果的和为1
    return X_exp / partition


# 对于任何随机输⼊，我们将每个元素变成⼀个⾮负数。此外，依据概率原理，每⾏总和为1。
X = torch.normal(0,1,(2, 5))
X_prob = softmax(X)
X,X_prob, X_prob.sum(1)

# 注意：
# 在数学上看起来是正确的，但矩阵中的⾮常⼤或⾮常⼩的元素可能造成数值上溢或下溢，没有采取措施来防⽌这点。

4、定义模型

'''
  4、定义模型
'''
def net(X):
    # 将每张原始图像展平为向量
    o = torch.matmul( X.reshape((-1,W.shape[0])), W) + b
    return softmax(o)

5、loss函数

'''
  5、定义loss函数

  交叉熵损失函数(cross_entropy)：这可能是深度学习中最常⻅的损失函数，因为⽬前分类问题的数量远远超过回归问题的数量。

  交叉熵采⽤真实标签的预测概率的负对数似然。
  这⾥我们不使⽤Python的for循环迭代预测（这往往是低效的），⽽是通过⼀个运算符选择所有元素。
'''


# 我们创建⼀个数据样本y_hat，其中包含2个样本在3个类别的预测概率，以及它们对应的标签y
y = torch.tensor([0, 2])
y_hat = torch.tensor([
    [0.1, 0.3, 0.6],
    [0.3, 0.2, 0.5]
])

# 有了y，我们知道在第1个样本中，第⼀类是正确的预测；⽽在第2个样本中，第三类是正确的预测。
# 然后使⽤y作为y_hat中概率的索引，我们选择第2个样本中第⼀个类的概率和第2个样本中第三个类的概率。
y_hat[
    [0, 1], y
]

6、分类精度

'''
  6、分类精度

分类精度即正确预测数量与总预测数量之⽐

1、⾸先，如果y_hat是矩阵，我们使⽤argmax获得每⾏中最⼤元素的索引来获得预测类别。

2、然后我们将预测类别与真实y元素进⾏⽐较。
由于等式运算符“==”对数据类型很敏感，因此我们将y_hat的数据类型转换为与y的数据类型⼀致。
结果是⼀个包含0（错）和1（对）的张量。最后，我们求和会得到正确预测的数量。
'''

def accuracy(y_hat, y):
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
         y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

'''
定义⼀个实⽤程序类Accumulator，⽤于对多个变量进⾏累加
'''
class Accumulator():

    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n


    def add(self, *args):
        self.data = [a + float(b) for a,b in zip(self.data, args)]


    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self,index):
        return self.data[index]

from AccumulatorClass import Accumulator

def evaluate_accuracy(net,data_iter):
    """计算在指定数据集上模型的精度"""
    if isinstance(net,torch.nn.Module):
        # 将模型设置为评估模式
        net.eval()
    metric = Accumulator(2)
    with torch.no_grad():
        for X,y in data_iter:
            metric.add(accuracy(net(X),y), y.numel())

    return metric[0] / metric[1]

7、模型的训练

'''
  7、模型的训练

  重构训练过程的实现以使其可重复使⽤。
'''

# 定义⼀个函数来训练⼀个迭代周期
# updater是更新模型参数的常⽤函数，它接受批量⼤⼩作为参数。它可以是sgd函数，也可以是框架的内置优化函数。
def epoch_train(net,train_iter,loss,updater):
    # 将模型设置为训练模式
    if isinstance(net,torch.nn.Module):
        net.train()

    # 指标：训练损失总和，训练准确度总和，样本数
    metric = Accumulator(3)
    for X,y in train_iter:
        # 计算梯度，并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)

        if isinstance(updater, torch.optim.Optimizer):
            # 使用pytorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])

        metric.add(
            float(l.sum()),
            accuracy(y_hat,y),
            y.numel()
        )

    # 返回训练损失和训练精度
    return (metric[0] / metric[2],metric[1] / metric[2])

# 接下来我们实现⼀个训练函数，它会在train_iter访问到的训练数据集上训练⼀个模型net。
# 该训练函数将会运⾏多个迭代周期（由num_epochs指定）。
# 在每个迭代周期结束时，利⽤test_iter访问到的测试数据集对模型进⾏评估。

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
    for epoch in range(num_epochs):
        print(f"epoch: {epoch + 1}")
        train_metrics = epoch_train(net,train_iter,loss,updater)
        print(train_metrics[0],train_metrics[1])
        test_acc = evaluate_accuracy(net,test_iter)
        print(test_acc)

# 使用⼩批量随机梯度下降来优化模型的损失函数，设置学习率为0.1。
lr = 0.1

# 小批量随机梯度下降
def mini_batch_sgd(params, lr, batch_size):

    # torch.no_grad是一个类一个上下文管理器，disable梯度计算。
    # disable梯度计算对于推理是有用的，当你确认不会调用Tensor.backward()的时候。这可以减少计算所用内存消耗。
    # 这个模式下，每个计算结果的requires_grad=False，尽管输入的requires_grad=True。
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

def updater(batch_size):
    return mini_batch_sgd([W, b], lr, batch_size)

# 我们训练模型10个迭代周期。请注意，迭代周期（num_epochs）和学习率（lr）都是可调节的超参数。
num_epochs = 10

train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

8、模型的预测

'''
8、模型的预测
'''
def get_fashion_mnist_labels(labels):
    """返回Fashion-MNIST数据集的⽂本标签"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]


def predict_ch3(net,test_iter, n=8):

    for X,y in test_iter:
        trues = get_fashion_mnist_labels(y[0:n])
        preds = get_fashion_mnist_labels(
        net(X).argmax(axis=1)[0:n]
    )

        print('trues:',trues)
        print('preds:',preds)
        break


predict_ch3(net,test_iter)

3、softmax回归的pytorch实现

1、读取服装分类数据集 Fashion-MNIST

'''
通过深度学习框架的⾼级API实现softmax回归模型
'''
import torchvision
import torch
from torch import nn
from torch.utils import data
from torchvision import transforms

'''
1、加载服装分类数据集

'''
def get_dataloader_workers():
    """使⽤4个进程来读取数据"""
    return 4



def get_mnist_data(batch_size, resize=None):
    trans = [transforms.ToTensor()]

    if resize:
        # 还接受⼀个可选参数resize，⽤来将图像⼤⼩调整为另⼀种形状
        trans.insert(0,transforms.Resize(resize))
    trans = transforms.Compose(trans)

    mnist_train = torchvision.datasets.FashionMNIST(
        root='../data',train=True,transform=trans,download=False
    )


    mnist_test = torchvision.datasets.FashionMNIST(
        root='../data',train=False,transform=trans,download=False
    )
    # 数据加载器每次都会读取⼀⼩批量数据，⼤⼩为batch_size。通过内置数据迭代器，我们可以随机打乱了所有样本，从⽽⽆偏⻅地读取⼩批量
    # 数据迭代器是获得更⾼性能的关键组件。依靠实现良好的数据迭代器，利⽤⾼性能计算来避免减慢训练过程。
    train_iter = data.DataLoader(mnist_train,batch_size=batch_size,shuffle=True,num_workers=get_dataloader_workers())
    test_iter = data.DataLoader(mnist_test,batch_size=batch_size,shuffle=True,num_workers=get_dataloader_workers())

    return (train_iter,test_iter)


batch_size = 256

train_iter,test_iter = get_mnist_data(batch_size)

2、初始化模型参数

'''
2、初始化模型参数

softmax回归的输出层是⼀个全连接层。因此，为了实现我们的模型，我们只需在Sequential中添加⼀个带有10个输出的全连接层。

同样，在这⾥Sequential并不是必要的，但它是实现深度模型的基础。我们仍然以均值0和标准差0.01随机初始化权重。
'''


# pytorch不会隐式调整输入的形状，因此在线性层前定义展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))


def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

3、loss函数

在前⾯，我们计算了模型的输出，然后将此输出送⼊交叉熵损失。从数学上讲，这是⼀件完全合理的事情。然⽽，从计算⻆度来看，指数可能会造成数值稳定性问题。
因为如果ok中的⼀些数值⾮常⼤，那么exp(ok)可能⼤于数据类型容许的最⼤数字，即上溢（overflow）。这将使分⺟或分⼦变为inf（⽆穷⼤），最后得到的是0、inf或nan（不是数字）的yˆj。在这些情况下，我们⽆法得到⼀个明确定义的交叉熵值。

解决这个问题的⼀个技巧是：在继续softmax计算之前，先从所有ok中减去max(ok)。

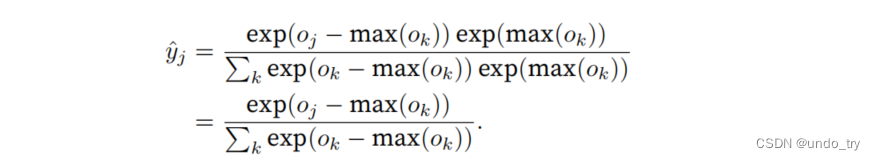
在减法和规范化步骤之后，可能有些oj − max(ok)具有较⼤的负值。由于精度受限，exp(oj − max(ok))将有接近零的值，即下溢（underflow）。这些值可能会四舍五⼊为零，使yˆj为零，并且使得log(ˆyj )的值为-inf。反向传播⼏步后，可能会发现可怕的nan结果。

尽管我们要计算指数函数，但我们最终在计算交叉熵损失时会取它们的对数。通过将softmax和交叉熵结合在⼀起，可以避免反向传播过程中可能会困扰我们的数值稳定性问题。

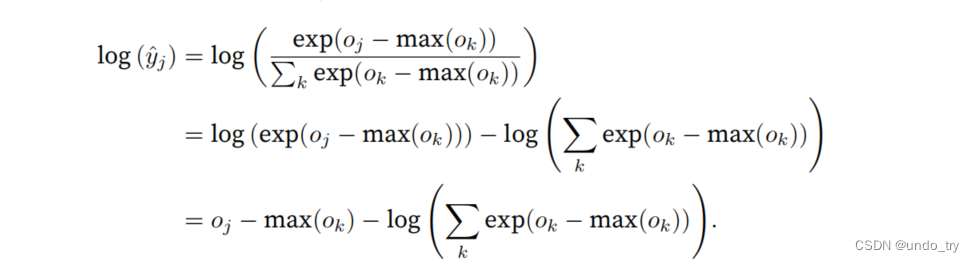
我们也希望保留传统的softmax函数，以备我们需要评估通过模型输出的概率。但是，我们没有将softmax概率传递到损失函数中，⽽是在交叉熵损失函数中传递未规范化的预测，并同时计算softmax及其对数。

loss = nn.CrossEntropyLoss(reduction='none')

4、梯度下降

'''
4、梯度下降算法

我们使⽤学习率为0.1的⼩批量随机梯度下降作为优化算法。这与我们在线性回归例⼦中的相同，这说明了优化器的普适性
'''

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

5、模型的训练

'''
5、训练
'''

def accuracy(y_hat, y):
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
         y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

from AccumulatorClass import Accumulator

def evaluate_accuracy(net,data_iter):
    """计算在指定数据集上模型的精度"""
    if isinstance(net,torch.nn.Module):
        # 将模型设置为评估模式
        net.eval()
    metric = Accumulator(2)
    with torch.no_grad():
        for X,y in data_iter:
            metric.add(accuracy(net(X),y), y.numel())

    return metric[0] / metric[1]

def epoch_train(net,train_iter,loss,updater):
    # 将模型设置为训练模式
    if isinstance(net,torch.nn.Module):
        net.train()

    # 指标：训练损失总和，训练准确度总和，样本数
    metric = Accumulator(3)
    for X,y in train_iter:
        # 计算梯度，并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)

        if isinstance(updater, torch.optim.Optimizer):
            # 使用pytorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])

        metric.add(
            float(l.sum()),
            accuracy(y_hat,y),
            y.numel()
        )

    # 返回训练损失和训练精度
    return (metric[0] / metric[2],metric[1] / metric[2])

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
    for epoch in range(num_epochs):
        print(f"epoch: {epoch + 1}")
        train_metrics = epoch_train(net,train_iter,loss,updater)
        print(train_metrics[0],train_metrics[1])
        test_acc = evaluate_accuracy(net,test_iter)
        print(test_acc)

    train_loss,train_acc = train_metrics
    assert train_loss < 0.5,train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc


num_epochs = 10

train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)
# 和以前⼀样，这个算法使结果收敛到⼀个相当⾼的精度，⽽且这次的代码⽐之前更精简

6、模型的预测

'''
6、模型的预测
'''
def get_fashion_mnist_labels(labels):
    """返回Fashion-MNIST数据集的⽂本标签"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]


def predict_ch3(net,test_iter, n=8):

    for X,y in test_iter:
        trues = get_fashion_mnist_labels(y[0:n])
        preds = get_fashion_mnist_labels(
        net(X).argmax(axis=1)[0:n]
    )

        print('trues:',trues)
        print('preds:',preds)
        break


predict_ch3(net,test_iter)

最后

以上就是尊敬帽子为你收集整理的pytorch基础操作(四)softmax回归手动实现以及pytorch的API实现的全部内容，希望文章能够帮你解决pytorch基础操作(四)softmax回归手动实现以及pytorch的API实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。