前言
众所周知,算法题主要有两大难点,一是「实现」,即算法本身的难度;二是「思路」,即你能否想到使用这个算法来解决题目。
并且对于有一定刷题基础的同学来说,力扣上大部分简单、中等题所涉及的算法都是非常常见的算法,即算法本身不存在难度,最大的难点在于「思路」,即如何想到适合本题的算法。
而解决「思路」问题,除了大量刷题积累经验之外,还可以采用一定的「巧劲」,从时间复杂度这个角度入手筛选出合适的算法。而本文的主要目的就是向大家介绍这种「巧劲」是如何在具体解题过程中发挥作用的。
本文一共分成三个部分,具体内容框架如下所示:
数据范围的隐含信息
如何确定一道题合适的时间复杂度?最简单、快捷的方式就是通过观察题目中的数据范围来确定。
不过你可能马上会反驳,力扣上并不是所有题目都有数据范围,那又该如何确定呢?
不要急噢,没有数据范围也是可以采用这种方式来思考的,我们会在「练习」部分进行详细说明。
言归正传,如何通过数据范围来确定合适的时间复杂度呢?
通常来说,在力扣上,Python 可以支持到 1 0 7 10^7 107 的时间复杂度;C++ 会稍微多一点,大概 1 0 7 ∼ 1 0 8 10^7sim10^8 107∼108 之间。因此我们可以得到如下表所示的,数据范围与算法大致时间复杂度的对应表。
| 数据范围 | 时间复杂度 |
|---|---|
| 20 | O ( 2 n ) O(2^n) O(2n) |
| 50 | O ( n 4 ) O(n^4) O(n4) |
| 200 | O ( n 3 ) O(n^3) O(n3) |
| 2000 | O ( n 2 ) O(n^2) O(n2) |
| 20000 | O ( n l o g n ) O(nlogn) O(nlogn) |
| 50000 | O ( n ) O(n) O(n) |
算法时间复杂度总结
通过数据范围得到时间复杂度后,我们需要对照下图筛选出适合的算法进行求解。
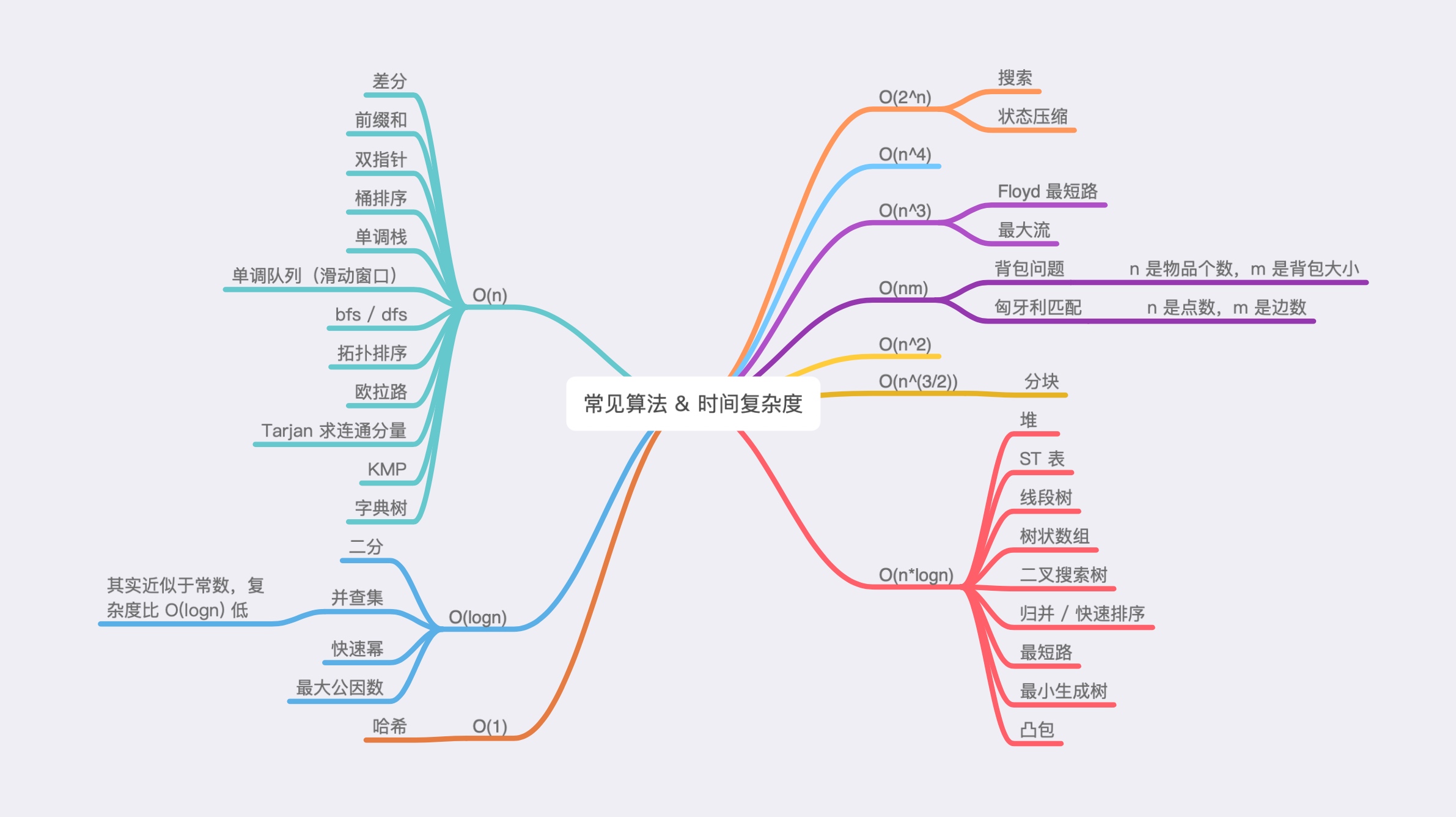
此处有两点需要注意:
- 上图仅列出了时间复杂度较为固定的常见算法,而类似于动态规划、贪心、暴力等时间复杂度百变多样的算法并未列出。
- O ( l o g n ) O(logn) O(logn) 的算法通常与 O ( n ) O(n) O(n) 的算法组合在一起,用于实现 O ( n l o g n ) O(nlogn) O(nlogn) 要求的题目。
练习
在讲解具体题目之前,我们先明确一下根据时间复杂度做题的具体流程:
-
根据数据范围选择时间复杂度
-
根据时间复杂度选择对应的常见算法集合
-
思考题目特征,从集合中选出合适的算法
-
根据选出的算法求解题目
接下来我们从「2020-04月 每日一题」中选取三道题用于该流程的练习。
1248. 统计「优美子数组」
题目描述
给你一个整数数组 nums 和一个整数 k。
如果某个连续子数组中恰好有 k 个奇数数字,我们就认为这个子数组是「优美子数组」。
请返回这个数组中「优美子数组」的数目。
示例 1:
输入:nums = [1,1,2,1,1], k = 3
输出:2
解释:包含 3 个奇数的子数组是 [1,1,2,1] 和 [1,2,1,1] 。
示例 2:
输入:nums = [2,4,6], k = 1
输出:0
解释:数列中不包含任何奇数,所以不存在优美子数组。
示例 3:
输入:nums = [2,2,2,1,2,2,1,2,2,2], k = 2
输出:16
数据范围
1 <= nums.length <= 50000
1 <= nums[i] <= 10^5
1 <= k <= nums.length
解决过程
- 数据范围 => 时间复杂度
本题的数据范围到达了 50000,因此我们将时间复杂度划定在 O ( n ) O(n) O(n) 的范围内。
- 时间复杂度 => 常见算法集合
根据上述「常见算法 & 时间复杂度」图,我们可以划定本题的算法集合。由于此题明显是数组上操作的问题,因此我们仅列出 O ( n ) O(n) O(n) 范围内关于数组的算法。
差分、前缀和、双指针、桶排序、单调栈、单调队列
- 思考题目特征 => 从集合中选出合适算法
仔细观察题干,可以发现本题有两大关键特征:
- 连续子数组
- 子数组内恰好有 k 个奇数数字
如果对「前缀和」算法有所掌握的话,凭借这两大特征不难确定此题可以用「前缀和」求解。
令
s
u
m
[
i
]
sum[i]
sum[i] 表示数组第 0 个数到第 i 个数中奇数的个数,因此区间 [l, r] 符合题意,当且仅当下式成立:
s
u
m
[
r
]
−
s
u
m
[
l
−
1
]
=
k
sum[r]-sum[l-1]=k
sum[r]−sum[l−1]=k
由此我们可以令
m
p
[
x
]
mp[x]
mp[x] 表示有多少个节点
i
i
i 满足
s
u
m
[
i
]
=
x
sum[i]=x
sum[i]=x。然后从左向右枚举,当求得第
i
i
i 个点的
s
u
m
sum
sum 值后,更新
m
p
[
s
u
m
[
i
]
]
mp[sum[i]]
mp[sum[i]] 数组,并计算有多少个 l 满足区间 [l, i] 符合题意。累加答案即可得到最终结果,具体实现可参看下述代码。
C++ 代码实现
class Solution {
vector<int> mp;
public:
int numberOfSubarrays(vector<int>& nums, int k) {
int sum = 0, ans = 0, n = nums.size();
mp.resize(n + 2, 0);
mp[0] = 1;
for(auto y:nums){
if(y % 2) sum++;
mp[sum]++;
if(sum-k >= 0) ans += mp[sum-k];
}
return ans;
}
};
面试题 08.11. 硬币
题目描述
硬币。给定数量不限的硬币,币值为 25 分、10 分、5 分和 1 分,编写代码计算 n 分有几种表示法。(结果可能会很大,你需要将结果模上 1000000007)
示例 1:
输入: n = 5
输出:2
解释: 有两种方式可以凑成总金额:
5=5
5=1+1+1+1+1
示例 2:
输入: n = 10
输出:4
解释: 有四种方式可以凑成总金额:
10=10
10=5+5
10=5+1+1+1+1+1
10=1+1+1+1+1+1+1+1+1+1
数据范围
0 <= n (总金额) <= 1000000
解决过程
- 数据范围 => 时间复杂度
本题的数据范围到达了 1000000,因此我们将时间复杂度划定在 O ( n ) O(n) O(n) 的范围内。再仔细观察一下 「常见算法 & 时间复杂度」图,可以发现由于只有 4 种面值的硬币,因此 O ( n m ) O(nm) O(nm) 的背包也是可行的。
- 时间复杂度 => 常见算法集合
根据时间复杂度与「常见算法 & 时间复杂度」图,我们可以划定本题的算法集合。由于此题明显与图论、字符串等算法无关,因此我们仅列出 O ( n ) O(n) O(n)、 O ( n m ) O(nm) O(nm) 范围内有一定可能性的算法。
差分、前缀和、双指针、桶排序、单调栈、单调队列、背包问题
- 思考题目特征 => 从集合中选出合适算法
仔细观察此题,可以发现如下几个特征:
- 四类硬币
- 每类硬币数量不限
- 求组成 n 的方案数
如果对「动态规划」有一定熟悉度的话,基本可以确定此题就是「动态规划问题」,因此本题具有很明显的「子结构」性质。
然后再根据之前确定的时间复杂度 O ( n ) O(n) O(n)、 O ( n m ) O(nm) O(nm),以及我们选出的算法,基本可以确定该动态规划问题的状态,只有如下两种:
- f [ i ] f[i] f[i] 表示用四种硬币组成 i 分的方案数,属于典型线性 DP
- f [ i ] [ j ] f[i][j] f[i][j] 表示用前 i 种硬币组成 j 分的方案数,属于背包问题
再仔细思考两种状态的转移方程,可以发现第二种采用背包思路的 DP 状态更适合解决本题,且由于硬币个数不限,因此是经典的「完全背包」问题。
所以我们可以直接列出如下的转移方程( c o i n [ i ] coin[i] coin[i] 表示第 i 类硬币的面值):
f[i][j] = f[i-1][j]
f[i][j] = f[i][j] + f[i][j-coin[i]]
可以发现, f [ i ] [ j ] f[i][j] f[i][j] 的数值主要由 f [ i − 1 ] [ j ] f[i-1][j] f[i−1][j] 与 f [ i ] [ j − c o i n [ j ] ] f[i][j-coin[j]] f[i][j−coin[j]] 得到,因此我们可以压缩掉第一维,即采用滚动数组的方法,得到如下方程:
f[j] = f[j] + f[j-coin[i]]
由于「完全背包」是背包问题中的经典模型,因此更具体的细节,大家可以参考下述代码。
C++ 代码实现
class Solution {
vector<int> f;
int coin[4] = {25, 10, 5, 1}, mod = 1e9+7;
public:
int waysToChange(int n) {
f.resize(n + 2, 0);
f[0] = 1;
for(int i = 0; i < 4; i++)
for(int j = coin[i]; j <= n; j++)
f[j] = (f[j] + f[j-coin[i]]) % mod;
return f[n];
}
};
56. 合并区间
题目描述
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
解决过程
- 数据范围 => 时间复杂度
现在我们来解决最开头提到的那个问题,「力扣上并不是所有题目都有数据范围,那又该如何确定呢?」。此题就属于没有数据范围的题目,并且在很多面试题中,也都是没有数据范围的,这时应该怎么办呢?
根据经验,对于此类没有数据范围的题目,我们通常需要自行从小到大枚举数据范围,一般从 O ( n ) O(n) O(n) 开始枚举,并且大部分的题枚举到 O ( n l o g n ) O(nlogn) O(nlogn) 时就能找到合适的算法。
因此对于此题,我们暂且将时间复杂度限制在 O ( n ) ∼ O ( n l o g n ) O(n)sim O(nlogn) O(n)∼O(nlogn) 之间。
- 时间复杂度 => 常见算法集合
有了时间复杂度之后,我们就可以根据「常见算法 & 时间复杂度」图划定算法集合。由于此题明显与图、计算几何、字符串无关,因此我们可以大致确定如下的算法集合。
差分、前缀和、双指针、桶排序、单调栈、单调队列、堆、ST 表、线段树、树状数组、排序
- 思考题目特征 => 从集合中选出合适算法
仔细观察此题,可以发现本题题意很明确,就是合并重叠区间,那怎样的区间算重叠呢?
现有两个区间,分别为 [l1, r1]、[l2, r2],假设 l1 <= l2,则当 l2 <= r1 时,两个区间发生重叠。
此时再根据上述选出的算法集合,一一排除、筛选,不难发现本题可用「排序」解决。即对于所有区间,按照左端点排序,然后从左到右枚举所有区间,对于区间 i 来说,l[i-1] <= l[i],则我们只需判断 l[i] <= r[i-1] 是否成立。如果成立,则合并两个区间,否则不合并。
由此我们便可以通过「排序」算法解决此题,具体的代码细节如下所示。
C++ 代码实现
class Solution {
vector<vector<int>> ans;
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end());
for (auto y:intervals) {
int l = y[0], r = y[1];
if (!ans.size() || ans.back()[1] < l)
ans.push_back({l, r});
else
ans.back()[1] = max(ans.back()[1], r);
}
return ans;
}
};
总结
最后,我们来总结一下「数据范围」=> 「最终算法」的总体过程,如下图所示。
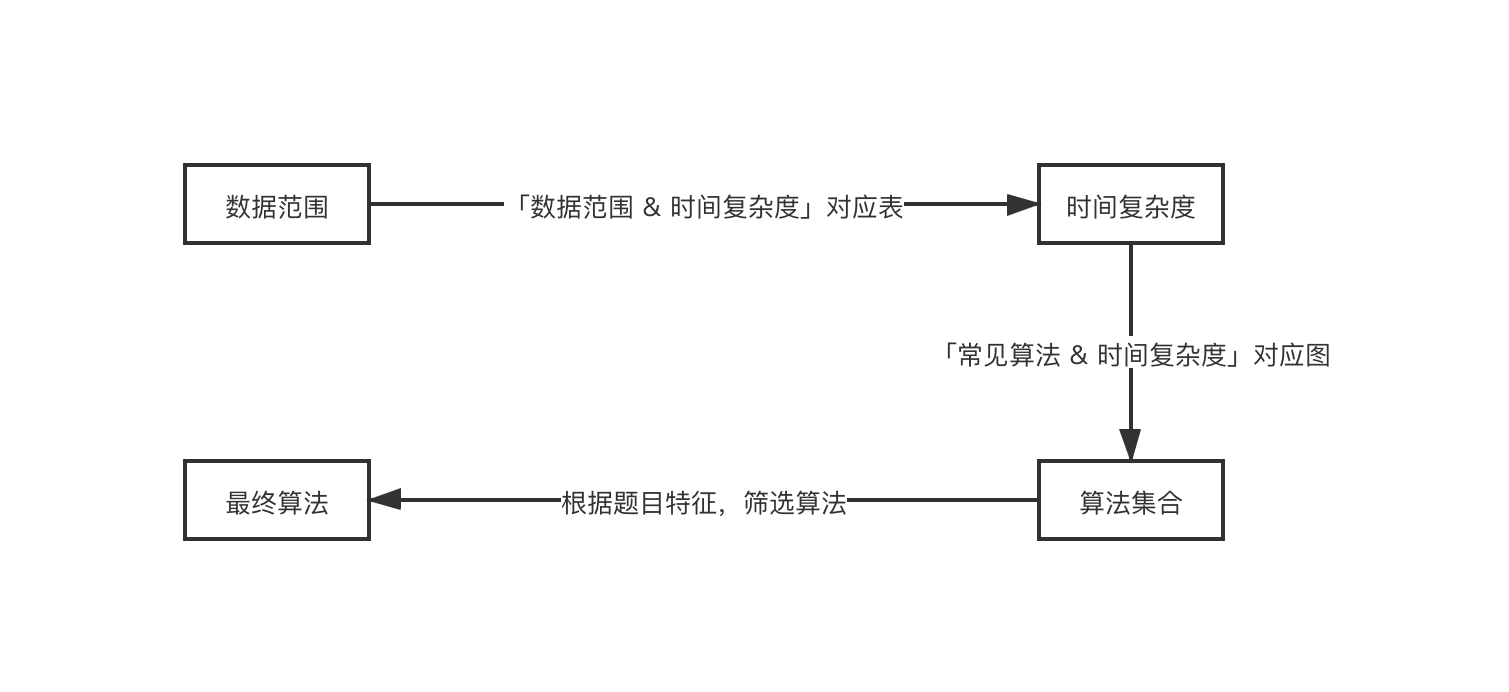
除此之外,还需注意,从「数据范围」入手思考「最终算法」只是获取题目思路的手段之一,并且在上述流程图中,「根据题目特征,筛选算法」是最为关键的步骤,这不仅要求做题者具有「挖掘题目特征」的能力,更要求做题者对于「常见算法」要有一定的熟悉度。
也正是因为这个原因,「常见算法 & 时间复杂度」对应图是具有个人特征的。每个人由于掌握的算法不同,「常见算法 & 时间复杂度」图也各不相同,因此希望大家能够有意识地构建属于自己的「常见算法 & 时间复杂度」图,并在刷题的过程中,不断更新,不断完善。力求能够在遇到自己掌握范围内的算法题时,一举击破。
最后的最后,祝大家刷题愉快,能力蹭蹭蹭往上涨。(๑•̀ㅂ•́)و✧
ps:大家要坚持「每日一题」哟~
最后
以上就是爱笑蚂蚁最近收集整理的关于有什么相见恨晚的算法答题套路?【力扣】的全部内容,更多相关有什么相见恨晚内容请搜索靠谱客的其他文章。








发表评论 取消回复