由于工作变动原因，这次翻译拖的时间比较长……抱歉啦！

其实也是由于每章的内容越来越多了，很难在短时间内翻译完，是个很磨人的事情。

不过我会坚持下去的！希望能更多地帮到大家吧！

业余翻译，若有不周到之处，还请多多指教。

实时渲染（第四版）Real-Time Rendering (Fourth Edition)

第6章 纹理化 Chapter 6 Texturing

“所需要做的仅是为了使渲染图像看起来正确。” —— 吉姆·布林

(注：吉姆·布林，美国计算机科学家，他的 Blinn-Phong 着色模型在业内无人不知，无人不晓）

表面的质感就是外观和感觉 —— 只要想一想油画的质感就知道了。在计算机图形学中，纹理化是获取表面并使用某些图片、函数或其他数据源在每个位置修改其外观的过程。例如，显示砖墙时，我们不是精确地去表示砖墙的几何形状，而是将砖墙的彩色图片应用于两个三角形组成的矩形上。查看矩形时，彩色图片会显示在矩形所在的位置。除非观察者很靠近墙壁，否则缺少的几何细节是不会引起注意的。

然而，某些带纹理的砖墙可能会因为缺乏几何形状而无法令人信服。例如，如果砂浆应该是哑光的（matte），而砖块是光滑的（glossy），则观察者会注意到两种材料的粗糙度相同。为了产生更令人信服的体验，我们可以在表面上应用第二个图片纹理。根据表面上的位置，此纹理可以更改墙壁的粗糙度，而不是更改表面的颜色。现在，砖和灰浆的图片纹理具有颜色，而新纹理具有粗糙度值。

观看者可能会看到现在所有砖块都是光滑的，而砂浆不是，但是请注意，每个砖块表面看起来都非常平坦。这看起来是不对的，因为砖的表面通常会有一些不规则的起伏。通过应用凹凸贴图（bump mapping），我们就可以改变砖块的着色法线，以便在渲染砖块时，使它们看起来并不十分平滑。这种纹理会扰动矩形原始表面法线的方向，以用于计算光照。

然而从低角度观看，这种凹凸不平的错觉可能会瓦解。砖块应突出在砂浆上方，以使其看不见。即使从直视角度看，砖块也应该将阴影投射到砂浆上。视差贴图（Parallax mapping）使用一张纹理让平面在渲染时似乎变形了，而视差遮蔽贴图（parallax occlusion mapping）将射线投射到高度场纹理上以提高真实感。位移贴图（Displacement mapping）通过修改形成模型的三角形高度来真正位移曲面。图 6.1 显示了带有颜色纹理和凹凸贴图的示例。

图6.1. 纹理化。将颜色和凹凸贴图应用于此鱼以增加其视觉细节水平。（图片由Elinor Quittner提供。）

 

这些是可以通过纹理解决的问题类型的示例，使用了越来越复杂的算法。在本章中，将详细介绍纹理化技术。首先，会介绍纹理化过程的一般框架。接下来，我们会专注于使用图片对表面进行纹理化处理，因为这是实时工作中最流行的纹理化形式。简要讨论了程序纹理，然后说明了使纹理影响表面的一些常用方法。

 

6.1 纹理化管线 The Texturing Pipeline

纹理化是一种用于有效地对表面材质的变化建模的技术(?)。探讨纹理化的一种方法是去思考单个着色像素在此过程中会发生什么。如上一章所述，我们通过考虑材料的颜色和灯光以及其他因素来计算着色。如上一章所述，通过考虑材质的颜色和灯光以及其他因素来计算着色。如果存在半透明物体的话，透明度也会影响采样。我们通过修改着色方程式中使用的值来进行纹理化。这些值的更改方式通常基于表面上的位置。因此，对于砖墙的示例，我们会根据表面位置，用砖墙图片中的相应颜色替换表面上任何点的颜色。图片纹理中的像素通常称为纹理像素（texels）（注：简称纹素），以区别于屏幕上的像素。粗糙度纹理会修改粗糙度值，而凹凸纹理会更改着色法线的方向，因此每个图片纹理都会改变着色方程式的结果。

纹理化过程可以通过概括的纹理管线来描述。稍后我们将介绍许多术语，但请振作精神：管线的每个部分都将被详细介绍。

在空间中的位置是纹理化过程的起点。该位置可以位于世界空间中，但通常位于模型的参照系中，因此随着模型的移动，纹理也随之移动。用 Kershaw 的术语 [884] 来描述，此空间点上已应用了投影函数（projector function），以便获得一组被称为纹理坐标（texture coordinates）的数值，这些数值将用于访问纹理。此过程称为映射（mapping），也通常被称为纹理映射（texture mapping）。有时纹理图片本身就被称为纹理贴图（texture map），尽管严格来说这并非正确。

在将这些新值用于访问纹理之前，可以使用一个或多个匹配函数将纹理坐标转换为纹理空间。这些纹理空间的位置用于从纹理中获取值，例如，它们可以是图片纹理中的数组索引，以便检索像素。然后，取回的值可能会通过值转换函数再次进行转换，最后，这些新值将用于修改曲面的某些属性，例如材质或着色法线。图 6.2 详细展示了应用单个纹理的过程。管线复杂的原因是每个步骤都为用户提供了有用的控件。应该注意的是，并非所有步骤都需要始终保持激活。

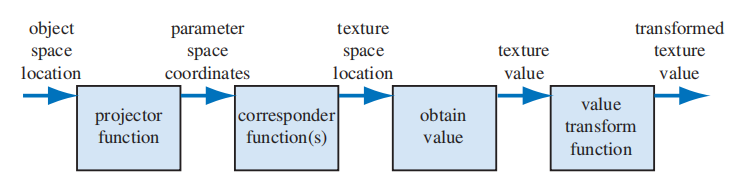
图 6.2. 单个纹理的概括纹理管线。

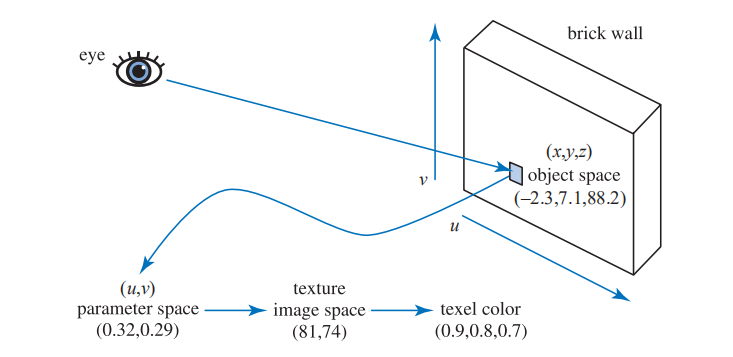
图 6.3. 砖墙的管线。

 

我们使用该管线，当三角形具有砖墙纹理并且在其表面上生成样本时，具体发生的事情如图（见图 6.3）。首先找到对象的局部参照系中的（x，y，z）位置； 假设是（−2.3，7.1，88.2）。然后将投影函数应用于此位置。正如世界地图是将三维对象投影到二维中一样，此处的投投影函数通常将（x，y，z）向量更改为二维向量（u，v）。此示例中使用的投影函数等效于正交投影（第2.3.1节），其作用类似于幻灯片投影仪，将砖墙图片照在三角形的表面上。回到墙这边，可以将其表面上的一个点转换为一对值，范围从 0 到 1 。这里假设获得的值为（0.32，0.29）。这些纹理坐标将用于查找此位置的图像颜色。我们砖墙纹理的分辨率为 256 × 256，因此匹配函数会将（u，v）分别乘以 256，得出（81.92，74.24）。弃掉小数点，在砖墙图片中对应像素为（81，74），它的颜色为（0.9，0.8，0.7）。纹理颜色位于 sRGB 颜色空间中，因此，如果要在着色方程式中使用该颜色，则将其转换为线性空间，得到（0.787，0.604，0.448）（第5.6节）。

 

6.1.1 投影函数 The Projector Function

纹理处理的第一步是获取表面的位置并将其投影到纹理坐标空间中，通常是二维（u，v）空间。建模包（Modeling packages）通常允许美术师定义每个顶点的（u，v）坐标。这些可以从投影函数或网格展开算法来初始化。美工可以用编辑顶点位置的相同方式来编辑（u，v）坐标。投影函数通常通过将空间中的三维点转换为纹理坐标来工作。建模程序中常用的投影函数包括球形投影，圆柱形投影和平面投影 [141、884、970]。

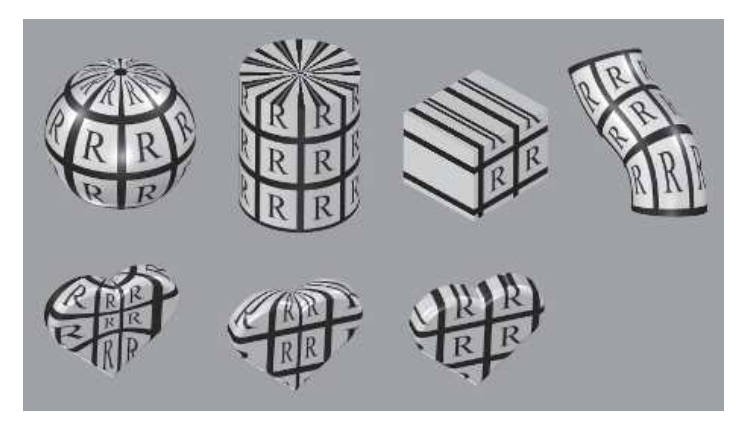
图 6.4. 不同的纹理投影。从左到右显示了球形，圆柱形，平面和自然（u，v）投影。底行显示了应用于单个对象（没有自然投影）的所有这些投影。

 

其他的输入可用于投影函数。例如，可以使用表面法线来选择将六个平面投影方向中的哪个用于该表面。面部相接处的接缝处会出现纹理匹配问题； Geiss [521，522] 讨论了一种将它们混合的技术。Tarini 等人 [1740]描述了多立方体贴图（polycube maps），其中一个模型被映射到一组立方体投影，而不同体积的空间映射到不同的立方体。

其他投影函数则不进行投影，但是它们是表面创建和细分（surface creation and tessellation）的隐含部分。例如，参数化曲面具有自然的（u，v）值集作为其定义的一部分。见图 6.4。纹理坐标也可以根据各种不同的参数生成，例如视图方向，表面温度或其他任何你能想到的参数。投影函数的目标是生成纹理坐标。将它们推导为位置的函数只是生成纹理坐标的一种方法。

非交互式渲染器通常将这些投影函数称为渲染过程本身的一部分。单个投影函数可能就足以满足整个模型的需要，但美术人员通常必须使用工具来划分模型并分别应用各种投影函数 [1345]。参见图 6.5。

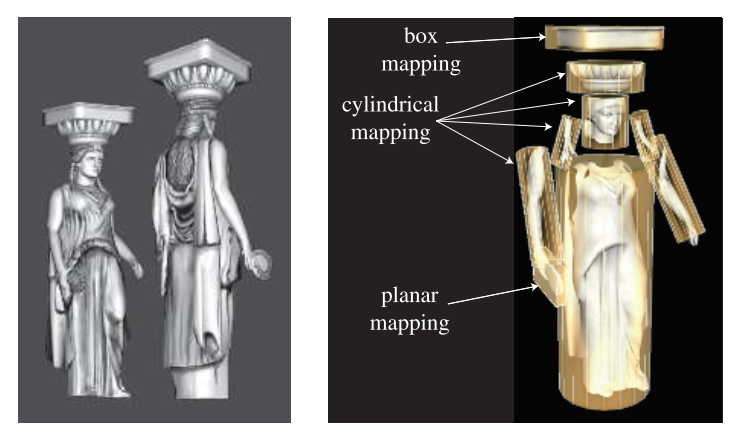
图 6.5. 各种纹理投影是如何被应用在单个模型上。盒式映射（Box mapping）由六个平面映射组成，每个盒子面都有一个映射。（图片由 Tito Pag´an 提供。）

 

在实时渲染中，通常在建模阶段应用投影函数，并将投影结果存储在顶点上。然而并非总是如此; 有时在顶点或像素着色器中应用投影函数也是有利的。这么做可以提高精度，并有助于启用各种效果，包括动画（第6.4节）。一些渲染方法，例如环境映射（environment mapping）（第10.4节），具有自己的专用的投影函数，并且这些函数都会逐像素进行计算。

球形投影（图 6.4 的左侧）将点投射到以某个点为中心的假想球体上。此投影与 Blinn 和 Newell 的环境映射方案（第10.4.1节）中使用的投影相同，因此第 407 页的公式 10.30 描述了此函数。这种投影方法也遇到了该部分所述的相同的顶点插值问题。

圆柱形投影计算的 u 纹理坐标与球形投影相同，而 v 纹理坐标计算为沿圆柱轴的距离。此投影对于具有自然轴的对象，例如旋转表面（surfaces of revolution），是很有用的。另外，当曲面与圆柱轴接近垂直时，会发生变形现象。

平面投影就像 X 射线一样，沿着一个方向进行平行投影，并将纹理应用于所有表面。它使用正交投影（第4.7.1节）。举个例子，这种类型的投影可用于贴花（decals）（第20.2节）。

由于投影方向边缘的曲面存在严重的变形，因此美术人员通常必须手动将模型分解为近似平面的部分。还有一些工具可通过展开网格，或是创建一组接近最佳的平面投影来帮助其最大程度地减少变形，或者通过其他方式辅助此过程。我们的目标是使每个多边形在纹理区域中享有更公平的份额，同时还要保持尽可能多的网格连接。连接性很重要，因为采样伪像（artifacts）可以沿着纹理的各个单独部分相遇的边缘出现。具有良好展开效果的网格也可以简化美术人员的工作 [970，1345]。16.2.1 节讨论了纹理变形如何对渲染产生不利影响。图 6.6 展示了用于创建图 6.5 中的雕像的工作空间。这种展开过程是网格参数化这一较大研究领域的一个方面。有兴趣的读者可以参考 Hormann 等人的 SIGGRAPH 课程笔记。[774]。

图 6.6. 雕像模型的几个较小的纹理，保存为两个较大的纹理。右图显示了三角形网格如何展开并显示在纹理上以帮助其创建。（图片由Tito Pag´an提供。）

 

纹理坐标空间并不总是二维平面。有时是三维体积。在这种情况下，纹理坐标表示为三元向量（u，v，w），其中 w 为沿投影方向的深度。其他系统最多使用四个坐标，通常指定为（s，t，r，q）[885]； q 用作齐次坐标中的第四个值。它的作用类似于电影或幻灯片的投影仪，投影纹理的大小随距离而增加。举个例子，对于将装饰性聚光图案（称为 gobo）投影到舞台或其他表面上来说，它是很有用的 [1597]。

纹理坐标空间的另一种重要类型是方向型，其空间中的每个点都可以通过输入方向访问。可视化这种空间的一种方法是将其作为单位球面上的点，每个点上的法线表示用于访问该位置纹理的方向。使用方向参数化的最常见纹理类型是立方体贴图（cube map
）（第6.2.4节）。

另外还值得注意的是，一维纹理图像和函数也有其用途。例如，在地形模型上，可以通过其高度确定颜色，例如低地是绿色，山峰是白色。线条也可以进行纹理化；其中一种用法是将雨水渲染为一组带有半透明图像的长线。此外，这种纹理对于从一个值转换为另一值，即作为查找表，也是有用的。

由于可以将多个纹理应用于一个表面，因此可能需要定义多组纹理坐标。但如果是应用坐标值的话，思路是相同的：这些纹理坐标在表面上插值并用于检索纹理值。然而在插值之前，这些纹理坐标会由匹配函数转换。

 

6.1.2 匹配函数 The Corresponder Function

匹配函数们将纹理坐标转换为纹理空间位置。它们提供了将纹理应用于表面的灵活性。匹配函数的一个应用案例就是使用 API 选择现有纹理的一部分进行显示；只有该子图像才会传递到后续操作流程中使用。

匹配函数的另一种类型是矩阵变换，可以将其应用于顶点或像素着色器。这样就可以在表面上平移，旋转，缩放，剪切或投影纹理。正如第 4.1.5 节所述，转换的顺序很重要。但令人惊讶的是，纹理转换的顺序必须与预期的顺序相反。这是因为纹理变换实际上会影响确定查看图像位置的空间。图像本身并不是要转换的对象；定义图片位置的空间正在被更改。

还有另一类匹配函数控制应用图像的方式。我们知道图像将出现在（u，v）处于 [0，1] 范围内的表面上。但是超出此范围会发生什么？此情况下匹配函数会确定其具体行为。在OpenGL中，这种类型的匹配函数被称为“包装模式”（wrapping mode）；在DirectX 中，它被称为“纹理寻址模式”（texture addressing mode）。这种类型的常见匹配函数分别是：

• 包裹（wrap)（DirectX），重复（repeat）（OpenGL），或图块 —— 图像在整个表面上重复；在算法上，将丢弃纹理坐标的整数部分。此函数对于使材质的图像重复并覆盖表面很有用，并且这通常是默认设置。
• 镜像（mirror）—— 图像在整个表面上重复，但在其他每个重复上都被镜像（翻转）。例如，图像通常从0到1出现，然后在1和2之间反转，然后在 2 和 3 之间正常，然后反转，依此类推。这可以让纹理边缘带有连续性。
• 夹取（clamp）（DirectX）或夹取到边缘（clamp to edge）（OpenGL）—— 超出 [0，1] 范围的值都将被夹取到该范围。这会导致图像纹理的边缘像素不断重复。此函数对于在纹理的边缘附近采用双线性插值时，避免意外地从纹理的相对边缘进行采样 [885] 很有用。
• 边框（border）（DirectX）或夹取到边框（clamp to border）（OpenGL）—— [0，1] 以外的纹理坐标使用单独定义的边框颜色进行渲染。例如，由于纹理的边缘将与边框颜色平滑融合，因此该函数可以很好地将贴图渲染到单色表面上。

图6.7.  图像纹理的包裹、镜像、夹取、边框函数的效果。

 

如图 6.7。可以为每个纹理轴不同地分配这些匹配函数，例如，纹理可以沿 u 轴重复并固定在 v 轴上。在 DirectX 中，还有一个单次镜像模式（mirror once mode），该模式沿着纹理坐标的零值镜像一次纹理，然后进行夹取，这对于对称贴花很有用。

重复平铺纹理是向场景添加更多视觉细节的廉价方法。但是，这种技术在重复大约三遍纹理后通常看起来并不令人信服，因为眼睛会挑选出重复图案。避免此类周期性问题的常见解决方案是将纹理值与另一个非平铺纹理组合。如在 Andersson [40] 描述的商业地形绘制系统中所见，这种方法可以被大大地扩展。在该系统中，会基于地形类型，高度，坡度和其他因素组合多个纹理。纹理图像还会与场景中放置几何模型位置相绑定，例如灌木和岩石。

避免周期性的另一种选择是使用着色器程序来实现专门的匹配函数，该函数随机地重新组合纹理图案或图块。王浩瓷砖（Wang tiles）是这种方法的一个例子。一个王浩瓷砖集是一小组具有匹配边缘的正方形瓦片。在纹理化过程中 [1860] 会随机选择图块。Lefebvre 和 Neyret [1016] 使用相关的纹理读取和表格来实现相似类型的匹配函数，以避图案重复。

应用的最后一个匹配函数边框（border）是隐含的，它是从图像的大小得出的。通常在 u 和 v 的 [0，1] 范围内应用纹理。如砖墙案例所示，通过在该范围内将纹理坐标乘以图像的分辨率，可以获取像素位置。能够在 [0，1] 范围内指定（u，v）值的优点在于，可以交换具有不同分辨率的图像纹理，而不必更改存储在模型顶点处的值。

 

6.1.3 纹理值 Texture Values

在使用匹配函数生成纹理空间坐标之后，会使用坐标去获取纹理值。对于图像纹理，这是通过访问纹理，并通过从图像中检索纹素信息来完成的。此过程将在 6.2 节中得到广泛的解决。图像纹理构成了实时渲染中绝大多数的纹理使用，但是也可以使用程序化函数（procedural functions）。在程序纹理化的情况下，从纹理空间位置获取纹理值的过程不涉及存储器查找，而是函数的计算。程序化纹理将在 6.3 节中进一步描述。

最直接的纹理值是用于替换或修改表面颜色的 RGB 三元组。类似地，可以返回单个灰度值。另一种要返回的数据是RGBα，如 5.5 节所述。α（α）值通常是颜色的不透明度，它确定颜色可能影响像素的程度。综上所述，也就是说，我们可以存储任何其他值，例如表面粗糙度。我们可以在图像纹理中存储许多其他类型的数据，这将在详细讨论凹凸贴图（bump mapping）时看到（第 6.7 节）。

从纹理返回的值可以在使用前进行转换。这些转换可以在着色器程序中执行。一个常见的例子是将数据从无符号范围（0.0 到 1.0）重新映射到有符号范围（-1.0 到 1.0），该范围用于对存储在颜色纹理中的法线进行着色。

 

6.2 图像纹理化 Image Texturing

在图像纹理化中，会将二维图像有效地粘贴到一个或多个三角形的表面上。我们已经完成了计算纹理空间位置的过程。现在，我们将解决在给定位置信息后，从图像纹理获取纹理值的相关问题和算法。在本章的其余部分中，图像纹理将简称为纹理（texture
）。另外，当我们在此处引用像素单元（pixel’s cell）时，是指围绕该像素的屏幕网格单元。如第 5.4.1 节所述，像素实际上是显示的颜色值，该颜色值可能（并且应该为了更好的质量）受到与其关联的网格单元外部的样本的影响。

在本节中，我们特别关注快速采样和纹理图像的滤波方法。第5.4.2节讨论了混叠的问题，特别是在渲染对象边缘方面。纹理也可能存在采样问题，但是它们发生在要渲染的三角形内部。

像素着色器通过将纹理坐标值传递给诸如 texture2D 之类的调用来访问纹理。这些值在（u，v）纹理坐标中，由对应功能映射到 [0.0，1.0] 范围。GPU 负责将此值转换为 texel 坐标。不同 API 中的纹理坐标系之间有两个主要区别。在 DirectX 中，纹理的左上角为（0，0），右下角为（1，1）。这与存储图像数据的图像类型匹配，顶行是指文件中的第一行。在OpenGL中，纹理像素（0，0）位于左下角，是 DirectX 的 y 轴翻转。像素具有整数坐标，但是我们经常要访问像素之间的位置，并在它们之间进行混合。这提出了像素中心的浮点坐标是什么的问题。Heckbert [692] 讨论了为何有两种可能的系统：截断（truncating）和四舍五入（rounding）。DirectX 9 将每个中心定义为（0.0，0.0）—— 使用四舍五入（rounding）。这个系统有些令人困惑，因为在DirectX 的原点，左上像素的左上角的值是（-0.5，-0.5）。DirectX 10 则向前更改为 OpenGL 的系统，在该系统上，纹理元素的中心具有小数值（0.5、0.5），即截断，或者更准确地讲，是向下取整（flooring），小数部分被丢弃。向下取整是一种更自然的系统，可以很好地映射到语言，例如，像素（5、9）为u坐标定义了 5.0 到 6.0 的范围，为 v 定义了 9.0 到 10.0 的范围。

关于这一点，还有一个值得解释的术语是从属纹理读取（dependent texture read），它有两个定义。第一种特别适用于移动设备。当通过 texture2D 或类似方法访问纹理时，每当像素着色器计算纹理坐标而不是使用从顶点着色器传入的未修改纹理坐标[66] 时，就会产生从属纹理读取。请注意，这意味着对传入的纹理坐标进行任何更改，甚至包括交换 u 和 v 值之类的简单操作。当着色器没有相关纹理读取时，较早的不支持 OpenGL ES 3.0 的移动 GPU 可以更有效地运行，因为这可以预先获取纹理像素数据。该术语的另一个较旧的定义对于早期的台式机 GPU 特别重要。在这种情况下，当一个纹理的坐标取决于某些先前纹理的值的结果时，就会发生从属纹理读取。例如，一种纹理可能会更改着色法线，进而改变用于访问立方体贴图的坐标。在早期的 GPU 上，这种功能受到限制甚至不存在。如今，此类读取可能会影响性能，具体取决于批处理中计算的像素数量以及其他因素。有关的更多信息，请参见第 23.8 节。

GPU 中使用的纹理图像大小通常为  纹理像素，其中 m 和 n 为非负整数。这些被称为二次幂（power-of-two，POT）纹理。现代 GPU 可以处理任意大小的非 2 幂（non-power-of-two，NPOT）纹理，从而可以将生成的图像视为纹理。但是，某些较旧的移动 GPU 可能不支持 NPOT 纹理的 mipmapping（第 6.2.2 节）。图形加速器对纹理大小有不同的上限。例如，DirectX 12 最多允许  个纹理像素。

假设我们有一个 256×256 纹理像素的纹理，并且我们想将其用作正方形的纹理。只要屏幕上投影的正方形与纹理的大小大致相同，正方形的纹理看起来就几乎是原始图像。但是，如果投影的正方形覆盖了原始图像的十倍像素（称为放大，magnification），或者投影的正方形仅覆盖了屏幕的一小部分（缩小，minification），会发生什么呢？ 答案是，这取决于你决定在这两种情况下使用哪种采样和滤波方法。

本章讨论的图像采样和滤波方法适用于从每个纹理读取的值。但是，我们期望的结果是防止最终渲染的图像出现走样，这在理论上要求对最终像素的颜色进行采样和滤波。这里的区别在于着色方程的输入的滤波，或输出的滤波。只要输入和输出是线性相关的（对于诸如颜色的输入来说就是如此），那么单个纹理值的滤波就等于最终颜色的滤波。但是，存储在纹理中的许多着色器输入值（例如表面法线和粗糙度值）与输出具有非线性关系。标准纹理滤波方法可能不适用于这些纹理，从而导致锯齿。在 9.13 节中讨论了用于此类纹理滤波的改进方法。

 

6.2.1 放大 Magnification

在图 6.8 中，将大小为 48×48 纹理像素的纹理贴到一个正方形上，并且相对于该纹理大小而言，该正方形的离观察者很近，因此基础图形系统必须放大该纹理。放大倍数最常用的滤波技术是最近邻（nearest neighbor）（实际滤波器称为 box 滤波器，请参见第 5.4.1 节）和双线性插值（bilinear interpolation）。还有三次卷积（cubic convolution），它使用 4× 4或 5×5 纹素阵列的加权和。这样可以实现更高的放大质量。尽管目前尚不普遍支持三次卷积（也称为双三次插值，bicubic interpolation）的本机硬件，但它可以在着色器程序中执行。

在图 6.8 的左侧，使用了最近邻方法。这种放大技术的一个特征是各个纹理像素可能变得明显。我们将该现象称为像素化（pixelation），这是因为该方法在放大时会采用最接近每个像素中心的纹理像素值，从而导致块状的外观。尽管此方法的质量有时很差，但每个像素仅需要提取一个纹理像素。

在中间的肖像图中，使用了双线性插值（有时称为线性插值）。对于每个像素，这种滤波都会找到四个相邻的纹理像素，并在二维上进行线性插值，以找到像素的混合值。可以看到，其结果是模糊的，与使用最近邻方法相比，产生的许多锯齿现象已消失。这里做个小实验，请在眯着眼睛的同时尝试看左边图像，因为此举的效果与低通滤波器大致相同，并且可以使脸部露出更多。(?)

图 6.8. 48×48 图像的纹理放大率为 320×320 像素。左：最近邻滤波，其中每像素选择最近的纹理像素。中：使用四个最近的纹理像素的加权平均值进行双线性滤波。右：使用 5×5 最近的纹理像素的加权平均值进行三次滤波。

返回到第 170 页的砖墙纹理示例（译者注：在 6.1 开头）：在不丢弃小数的情况下，我们获得了（pu，pv）=（81.92，74.24）。在这里我们使用 OpenGL 的左下原点纹理像素坐标系，因为它能与标准的直角坐标系相匹配。我们的目标是在四个最接近的纹理像素之间进行插值，并使用其纹理像素中心定义一个纹理像素大小的坐标系。见图 6.9。为了找到四个最近的像素，我们从样本位置减去像素中心值（0.5，0.5），得出（81.42，73.74）。丢弃小数部分，四个最接近的像素的范围从（x，y）=（81，73）到（x + 1，y + 1）=（82，74）。在我们的示例中，小数部分（0.42，0.74）是样本相对于由四个纹理像素中心形成的坐标系的位置。我们将此位置表示为（u'，v'）。

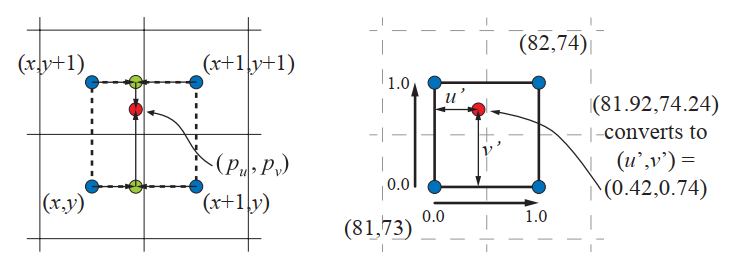
图 6.9. 双线性插值。涉及的四个纹理像素由左侧的四个正方形表示，纹理像素中心为蓝色。右边是由四个纹理像素的中心形成的坐标系。

将纹理访问函数定义为 t（x，y），其中 x 和 y 是整数，并返回纹理像素的颜色。可以将任何位置（u'，v'）的双线性插值颜色计算为两步过程。首先，水平（使用u'）对底部纹理像素t（x，y）和t（x + 1，y）进行插值，类似地，也对最顶部的两个纹理像素t（x，y + 1）和t（ x + 1，y + 1）进行插值。对于底部的纹理像素，我们获得（1 − u'）t（x，y）+ u't（x + 1，y）（图 6.9 中的底部绿色圆圈），对于顶部的像素，我们得出（1 − u'） t（x，y +1）+ u't（x +1，y +1）（上方的绿色圆圈）。然后使用 v' 对这两个值进行垂直插值，因此在  处的双线性插值颜色 为

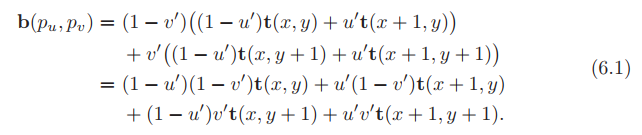
凭直觉，接近我们样本位置的纹理像素将对最终值产生更大的影响。这确实是我们在等式中所看到的。在（x + 1，y +1）处的右上纹理像素具有 u'v' 的影响。这里请注意对称性：右上的影响等于由左下角和采样点形成的矩形区域。回到我们的示例，这意味着从该纹理像素检索的值将乘以 0.42×0.74，特别是 0.3108。从该纹理像素的顺时针方向，其他乘数分别为 0.42×0.26、0.58×0.26 和 0.58×0.74，所有这四个权重的总和为1.0。

一种解决放大倍率模糊的常见方法是使用细节纹理（detail textures）。这些纹理代表了精细的表面细节，从手机上的划痕到地形上的灌木丛。这样的细节作为单独的纹理以不同的比例覆盖在放大的纹理上。细节纹理的高频重复图案与低频放大的纹理相结合，具有类似于使用单个高分辨率纹理的视觉效果。

双线性插值在两个方向上进行线性插值。但是，线性插值并不是我们想要的。假设纹理由棋盘图案中的黑白像素组成。使用双线性插值会得出整个纹理上变化的灰度样本。通过重新映射这一操作，例如，所有低于 0.4 的灰度都是黑色，所有高于 0.6 的灰度都是白色，并且中间的灰度都被拉伸以填充间隙，这样就可以让纹理看起来更像是棋盘，同时还使纹理像素之间有些融合 。参见图 6.10。

图 6.10. 最近邻，双线性插值，以及通过重新映射介于两者之间的情况，使用相同的2×2棋盘纹理。请注意，由于纹理和图像网格不完全匹配，最近邻采样会给出略有不同的正方形大小。

 

使用更高分辨率的纹理将具有相似的效果。例如，假设每个方格正方形由 4×4 的纹理像素而不是 1×1 组成。在每个方格的中心周围，插值的颜色将完全是黑色或白色。

在图 6.8 的右侧，已使用了双三次滤波器，剩余的块状现象已被大大消除。这里需要注意的是，双三次滤波器比双线性滤波器更昂贵。但是，许多高阶滤波器可以表示为重复线性插值 [1518]（另请参见第17.1.1节）。其结果，就是可以通过几次的查找来利用纹理单元中用于线性插值的 GPU 硬件。

如果认为双三次滤波器太昂贵，Qu´ılez [1451] 提出了一种简单技术，即使用平滑曲线在一组 2×2 纹素之间进行插值。我们首先描述曲线，然后描述技术。两条常用的曲线是平滑步幅曲线（smoothstep curve）和五阶曲线（quintic curve） [1372]：

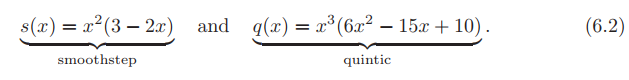
这些在许多其他情况下都很有用，在这些情况下，你需要从一个值平滑地插值到另一个值。平滑步幅曲线具有 s'（0）= s'（1）=  0 的特性，并且在 0 和 1 之间平滑。五阶曲线具有相同的特性，但是 q''（0）= q'' （1）= 0，即，曲线的起点和终点的二阶导数也为 0。两条曲线如图 6.11 所示。

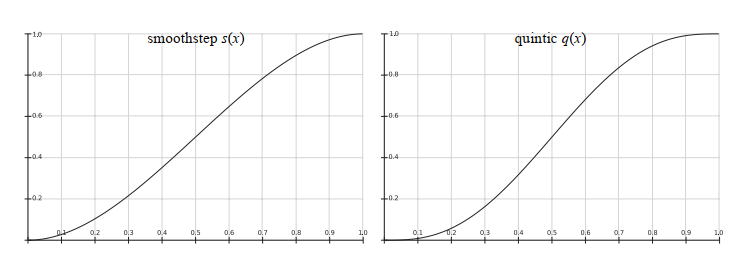
图 6.11. 平滑步幅曲线s（x）（左）和五阶曲线q（x）（右）。

该技术首先通过将样本乘以纹理尺寸并相加 0.5 来计算（u'，v'）（与公式 6.1 和图 6.9 中使用的相同）。保留整数部分以备后来使用，并将分数存储在 u' 和 v' 中，它们在 [0，1] 的范围内。然后将（u'，v'）变换为（tu，tv）=（q（u'），q（v'）），但仍在 [0，1] 的范围内。最后，减去 0.5，再将整数部分相加； 然后，将所得的 u 坐标除以纹理宽度，并以 v 进行类似的操作。此时，新的纹理坐标与 GPU 提供的双线性插值查找配合使用。请注意，此方法将在每个纹理像素处产生平稳状态，这意味着如果这些纹理像素位于 RGB 空间中的平面上，则此类型的插值将给出平滑但仍然呈阶梯状的外观，但这可能不是我们想要的。见图 6.12。

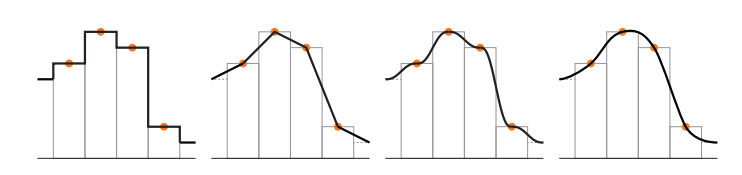
图 6.12. 四种放大一维纹理的方法。橙色圆圈表示纹理像素的中心以及纹理像素值（高度）。从左到右分别是：最近邻、线性、在相邻纹理像素之间使用五阶曲线、使用三次插值。

 

6.2.2 缩小 Minification

当纹理缩小时，多个纹理像素可能会覆盖像素的单元，如图 6.13 所示。为了获得每个像素的正确颜色值，您应该整合影响像素的纹理像素的效果。但是，很难精确地确定特定像素附近所有纹理像素的确切影响，并且实际上，我们不可能实时完美地做到这一点。

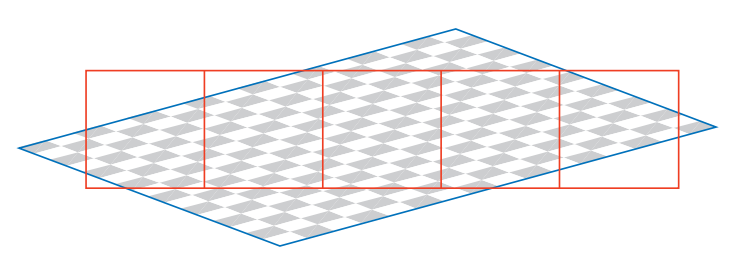
图 6.13. 缩小：通过一排像素单元的棋盘纹理的正方形视图，大致显示了许多纹理像素对每个像素的影响。

由于此限制，在 GPU 上使用了几种不同的方法。一种方法是使用最近邻的像素，它的工作原理与相应的放大滤波器完全相同，即，它选择在像素像元中心可见的纹理像素。该滤波器可能会导致严重的走样问题。在图 6.14 中，最上面的图使用了最近邻方法。在地平线上，会出现伪像，因为我们只选择了影响像素的许多纹理像素之一来表示表面。当表面相对于观察者移动时，这些伪像甚至会更加明显，并且这是我们说的时间性走样（temporal aliasing）的一种表现形式。

图 6.14. 顶部图像是通过点采样（最近邻）渲染的，中心是 mipmapping 渲染的，底部是求和区域表（summed area tables
）的渲染。

 

另一个经常被使用的滤波器是双线性插值，其工作原理与放大滤波器完全相同。该滤波器仅比最邻近的方法好一点点。它混合了四个纹理像素，而不是仅使用一个，但是当一个像素受到四个以上纹理像素的影响时，滤波器便会迅速失效并产生走样。

更好的解决方案是可能的。如 5.4.1 节所述，可以通过采样和滤波技术解决走样问题。纹理的信号频率取决于其纹理像素在屏幕上的间隔距离。由于奈奎斯特限制，我们需要确保纹理的信号频率不大于采样频率的一半。例如，一个图像是由交替的黑白线组成的，相隔一个纹理像素。波长为两个纹理像素宽（从黑线到黑线），因此频率为 。要在屏幕上正确显示此纹理，频率必须至少为 ，即每个纹理像素至少对应一个像素。因此，对于一般的纹理，每个像素最多应只有一个纹理像素，以避免走样。

为了达到这个目标，必须提高像素的采样频率或降低纹理频率。上一章讨论的反走样方法提供了提高像素采样率的方法。但是，这些仅会有限地增加采样频率。为了更充分地解决这个问题，目前已经开发了各种纹理缩小算法。

所有纹理反走样算法背后的基本思想是相同的：对纹理进行预处理并创建数据结构，这将有助于计算像素上一组纹理像素的效果的快速近似值。对于实时渲染，这些算法具有使用固定数量的时间和资源来执行的特征。用这种方式，每个像素会获取固定数量的样本，并将其组合起来以计算（可能很大）数量的纹理像素的效果。

 

Mip映射 Mipmapping 

最流行的纹理反走样方法称为 mipmapping [1889]。现在已生产的所有图形加速器均以某种形式实现了该功能。“ Mip”在细小语言中代表 multum，在拉丁语中则是“在一个小地方有很多东西”的名字。

当使用 mipmapping 最小化滤镜时，在进行实际渲染之前，使用一组较小版本的纹理增强原始纹理。纹理（零级）下采样（downsampled）到原始面积的四分之一，其中每个新的纹理像素值通常计算为原始纹理中四个相邻纹理像素的平均值。新的一级纹理有时称为原始纹理的子纹理。递归执行缩小操作，直到纹理的一个或两个尺寸等于一个纹理像素。此过程如图 6.15 所示。整个图像集通常称为 mipmap 链（mipmap chain）。

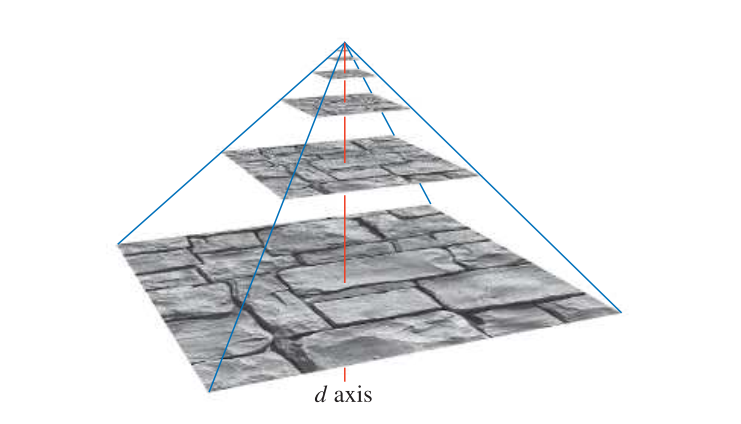
图 6.15. 通过在金字塔的底部拍摄原始图像（级别0），然后将每个 2×2 区域平均为下一级别的纹理像素值，即可形成 mipmap。垂直轴是第三纹理坐标 d。在该图中，d 不是线性的。它用于衡量样本用于插值的两个纹理级别。

 

形成高质量 Mipmap 的两个重要元素是良好的滤波和伽马校正。形成 Mipmap 级别的常见方法是获取每 2×2 组像素，并将它们平均以得到 Mip 像素值。这样操作的话，使用的滤波器便被称为 box 滤波器（box filter），它可能是最差的滤波器之一。这可能会导致质量差，因为它会不必要地模糊低频，同时保留一些会引起混叠的高频 [172]。最好使用高斯，Lanczos，Kaiser或类似的滤波器。快速，免费的源代码可用于任务 [172，1592]，并且某些 API 在 GPU 本身上支持更好的滤波。在纹理边缘附近，在滤波期间必须注意纹理是重复还是单个副本。

对于在非线性空间中编码的纹理（例如大多数颜色纹理），在滤波时忽略伽玛校正将会修改感知到的 Mipmap 级别的亮度 [173，607]。当你离对象越来越远并且使用了未经校正的 Mipmap 时，对象的整体外观可能会更暗，并且对比度和细节也会受到影响。因此，重要的是将此类纹理从 sRGB 转换为线性空间（第 5.6 节），在该空间中执行所有 mipmap 滤波，然后将最终结果转换回 sRGB 颜色空间进行存储。大多数 API 支持 sRGB 纹理，因此将在线性空间中正确生成 mipmap，并将结果存储在 sRGB中。访问 sRGB 纹理时，首先将它们的值转换为线性空间，以便正确执行放大和缩小。

正如之前提到的，某些纹理与最终着色颜色具有根本上的非线性关系。尽管这通常会给滤波带来问题，但由于要对数百或数千个像素进行滤波，因此 mipmap 的生成对此问题特别敏感。为了获得最佳的结果，通常需要专门的 mipmap 生成方法。此类方法在第 9.13 节中进行了详细说明。

构造纹理时访问此结构的基本过程很简单。屏幕像素将纹理自身上的区域包围起来。当像素区域投影到纹理上时（图 6.16），它包含了一个或多个纹理像素。严格地说，使用像素的单元格边界并不是正确的方法，但这里我们使用它来简化这个演示。单元外部的纹理像素可能会影响像素的颜色。请参阅第 5.4.1 节。我们的目的是大致确定多少的纹理会影响到像素。有两种用于计算 d 的常用量度（OpenGL 将其称为 λ，它也被称为细节纹理级别，texture level of detail）。一种方法是使用像素单元所形成的四边形的较长边缘，用它来近似像素的覆盖范围 [1889]； 另一种方法是使用四个微分 ∂u/∂x，∂v/∂x，∂u/∂y 和 ∂v/∂y 的最大绝对值作为度量 [901，1411]。每个微分是纹理坐标相对于屏幕轴的变化量的量度。例如，∂u/∂x 是一个像素的 u 纹理值沿 x 屏幕轴的变化量。有关这些方程式的更多信息，请参见Williams的原始文章 [1889] 或 Flavell [473] 或 Pharr [1411] 的文章。McCormack等。[1160] 讨论了通过最大绝对值方法会造成走样的问题，并提出了一个替代公式。Ewins等。[454] 分析了质量相当的几种算法的硬件消耗。

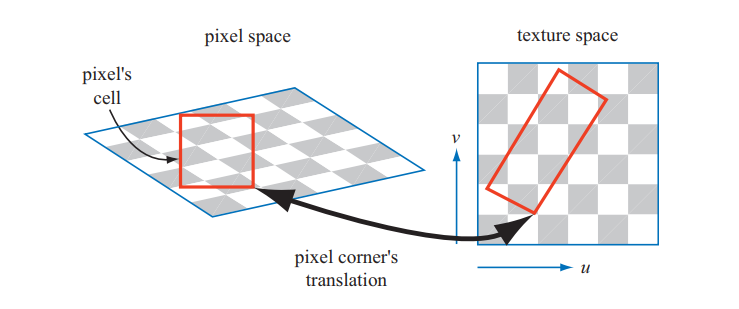
图 6.16. 左侧是一个正方形像素单元及其纹理视图。右边是像素单元在纹理本身上的投影。

 

使用 Shader Model 3.0 或更高版本的像素着色器程序可以使用这些渐变值。由于它们基于相邻像素值之间的差异，在受动态流控制（dynamic flow control）影响的像素着色器的某些部分中，我们无法访问它们（第 3.8 节）。为了在这样的部分中（例如，在循环内）执行纹理读取，必须较早地计算导数。请注意，由于顶点着色器无法访问渐变信息，因此在使用顶点纹理时，需要在顶点着色器本身中计算渐变或细节级别并将其提供给 GPU。

计算 d 坐标的目的是确定沿 mipmap 的金字塔轴采样的位置。见图 6.15。目标是达到奈奎斯特比率的像素与纹理像素比至少为1：1。这里的重要原理是，随着像素单元包含更多的纹理像素和 d 的增加，将访问更小，更模糊的纹理版本。（u，v，d）三元组用于访问 mipmap。值 d 与纹理级别类似，但是 d 是整数之间的距离的分数，而不是整数值。采样高于 d 位置的纹理级别和低于 d 位置的纹理级别。（u，v）位置用于从这两个纹理级别的每一个中检索双线性插值样本。然后再根据从每个纹理级别到 d 的距离对生成的样本进行线性插值。整个过程称为三线性插值（trilinear interpolation），是逐像素执行的。

d 坐标上的一个用户控制参数是细节偏差水平（level of detail bias，简称 LOD bias，LOD偏差）。这是与 d 相加的值，因此会影响纹理的相对清晰度。如果我们进一步向上移动金字塔以开始（增大d），则纹理将变得模糊。对于任何给定的纹理，良好的 LOD 偏差将随图像类型和使用方式而变化。例如，开始时有些模糊的图像可能会使用负偏差，而用于纹理化的滤波效果差（走样）的合成图像可能会使用正偏差。可以为纹理整体或像素着色器中的每个像素指定偏差。为了更好地控制，用户可以提供 d 坐标或用于计算它的导数。

mipmapping 的好处在于，访问并插值了预组合的像素集，而不是试图求和单独影响像素的所有纹理素。无论缩小多少，此过程都会花费固定的时间。但是，mipmapping 有几个缺陷 [473]。一个主要的缺陷是模糊。想象一下，一个像素单元在 u 方向上覆盖大量纹理像素，而在 v 方向上仅覆盖少数像素。这种情况通常发生在观看者近乎边缘地沿着带纹理的表面观看的时候。实际上，可能需要沿着纹理的一个轴进行最小化，而沿着另一个轴进行放大。访问 mipmap 的效果是检索了纹理上的正方形区域。无法检索矩形区域(?)。为避免产生走样，我们选择纹理上像素单元的近似覆盖率的最大度量。这导致检索到的样本通常相对模糊。在图 6.14 的 mipmap 图像中可以看到这种效果。移到右侧距离的线显示为模糊。

 

求和区域表 Summed-Area Table

避免过度模糊的另一种方法是求和区域表（SAT）[312]。要使用此方法，首先要创建一个数组，该数组的大小等于纹理的大小，但包含更多的颜色存储精度位（例如，红色，绿色和蓝色分别为 16 位或更多）。在此数组的每个位置，必须计算并存储由该位置和纹理像素（0，0）（原点）形成的矩形中所有相应纹理纹理像素的总和。在纹理化过程中，像素单元在纹理上的投影会被矩形所限制。然后访问求和区域表以确定该矩形的平均颜色，该颜色作为像素的纹理颜色传回。使用如图 6.17 所示的矩形的纹理坐标计算平均值。这可以使用公式 6.3 来完成：

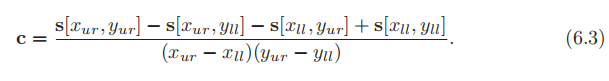
在此，x 和 y 是矩形的纹素坐标，而 s [x，y] 是该纹素的求和区域值。该方程的工作原理是：从右上角到原点，取整个区域的总和，然后通过减去相邻角的贡献减去面积 A 和 B 。区域 C 已被减去两次，因此将其添加到左下角。注意（，）是区域 C 的右上角，即（ + 1， + 1）是边界盒的左下角。

使用求和区域表的结果如图 6.14 所示。到达地平线的线在右侧边缘附近更加锐利，但中间的对角交叉线仍然模糊不清。问题在于，当沿着纹理的对角线观察纹理时，会生成一个大矩形，其中许多纹理像素不位于要计算的像素附近。例如，假设一个长而细的矩形代表像素单元的反投影，该像素按对角线横跨整个纹理，如图 6.17 所示。此时将返回整个纹理矩形的平均值，而不仅仅是像素单元内的平均值。

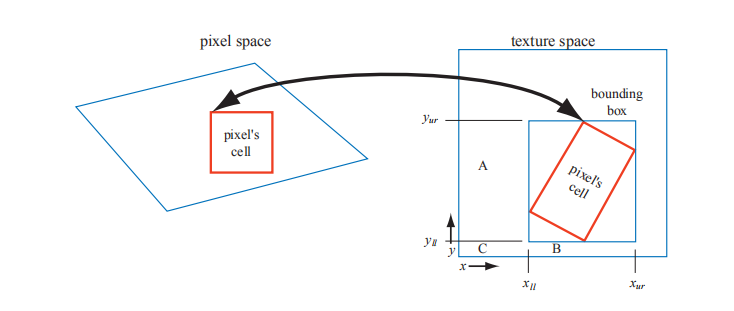
图 6.17. 像素单元反投影到纹理上，并以矩形为边界；矩形的四个角用于访问求和区域表。

 

求和区域表是所谓的各向异性滤波算法的一个示例 [691]。这样的算法在非正方形区域上检索纹理像素值。但是，SAT 能够在主要水平和垂直方向上最有效地做到这一点。还要注意，对于 16 × 16 或更小的尺寸的纹理，求和区域表至少需要两倍的内存，而较大的纹理则需要更高的精度。

求和区域表可以在现代 GPU 上实现，并以合理的整体内存成本提供更高的质量 [585]。改进的滤波对于高级渲染技术的质量至关重要。例如，Hensley 等。[718，719] 提供了一种有效的实现方式，并展示了求和区域采样如何改善光泽反射。可以通过 SAT 改进使用区域采样的其他算法，例如景深（depth of field） [585，719]，阴影图（shadow maps）[988] 和模糊反射（blurry reflections）[718]。

 

无约束各向异性滤波 Unconstrained Anisotropic Filtering

对于当前的图形硬件，进一步改善纹理滤波的最常用方法是重用现有的 mipmap 硬件。基本思想是对像素单元进行反投影，然后对纹理上的这个四边形（四边形）进行几次采样，然后合并采样。如上所述，每个 mipmap 样本都有一个位置和一个与其关联的正方形区域。该算法不使用单个 mipmap 样本来近似四边形的覆盖范围，而是使用几个正方形覆盖四边形。可以使用四边形的较短边来确定 d（与 mipmapping 不同，后者通常使用较长边）；这会使每个 Mipmap 样本的平均面积变小（从而减少模糊）。四边形的较长边用于创建平行于较长边并穿过四边形中间的各向异性线。当各向异性的量在 1：1 和 2：1 之间时，沿着这条线采集两个样本（见图 6.18）。在较高的各向异性比率下，沿轴将获取更多的样本。

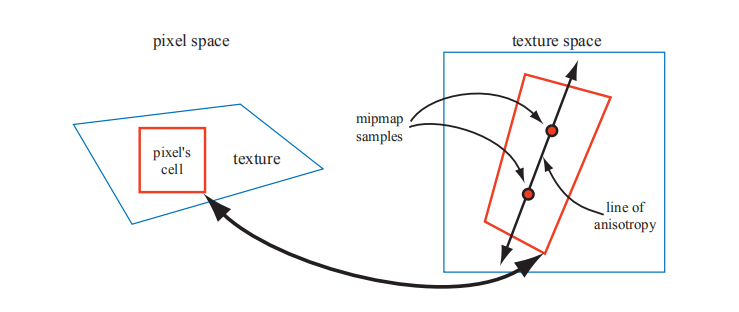
图 6.18. 各向异性滤波。像素单元的反投影产生四边形。在较长的侧面之间形成各向异性线。

 

该方案允许各向异性线沿任何方向延伸，因此没有求和区域表的限制。因为它使用 mipmap 算法进行采样，所以它也不需要比 mipmaps 更多的纹理内存。各向异性滤波的一个例子如图 6.19 所示。

图 6.19. Mipmap 与各向异性滤波。左侧完成了三线性 mipmapping，右侧进行了 16：1 各向异性滤波。展望未来，各向异性滤波可提供更清晰的结果，同时走样程度最小。（图片来自 three.js 示例webgl材料纹理各向异性 [218]。）

 

Schilling 等人首先提出了沿轴采样的想法。与他们的 Texram 动态存储设备 [1564]。Barkans 描述了该算法在 Talisman 系统中的用法 [103]。McCormack等人提出了一个类似的系统，称为Feline。[1161]。Texram的原始配方是沿各向异性轴（也称为探针）给予相同重量的样品。护身符在轴的相对两端将两个探针的重量减半。猫科动物使用高斯滤波器内核对一组探针加权。这些算法采用高质量的软件采样算法，例如椭圆加权平均（EWA）滤波器，该滤波器将像素的影响区域转换为纹理上的椭圆，并通过滤波器内核对椭圆内的纹理像素进行加权[691]。Mavridis和Papaioannou提出了几种在GPU上使用着色器代码实现 EWA 滤波的方法 [1143]。

 

6.2.3 体积纹理 Volume Textures

图像纹理的直接扩展是通过（u，v，w）（或（s，t，r）值）访问的三维图像数据。例如，医学成像数据可以被生成为三维网格。通过在该网格中移动多边形，可以查看这些数据的二维切片。一个相关的想法是用这种形式表示体积的灯光。通过找到其在该体积内的位置值以及光的方向，可以找到表面上某个点的照明。

大多数 GPU 支持对体积纹理进行 mipmapping。由于在体积纹理的单个 mipmap 级别内进行滤波涉及三线性插值，因此在 mipmap 级别之间进行滤波需要四线性插值。由于这涉及对 16 个纹理像素的结果进行平均，因此可能会导致精度问题，可以使用更高精度的体积纹理来解决。Sigg 和 Hadwiger  [1638] 讨论了与体积纹理有关的此问题和其他问题，并提供了执行滤波和其他操作的有效方法。

尽管体积纹理具有更高的存储要求，并且滤波成本更高，但它们确实具有一些独特的优势。由于可以将三维位置直接用作纹理坐标，因此可以跳过为三维网格找到良好的二维参数化的复杂过程。这避免了二维参数化中常见的变形和接缝问题。体积纹理也可以用于表示诸如木材或大理石的材料的体积结构。具有这种纹理的模型看起来是用这种材料雕刻而成的。

由于不使用绝大多数样本，因此使用体积纹理进行表面纹理化的效率极低。Benson 和 Davis [133] 和 DeBry 等人。[334] 讨论了在稀疏八叉树（sparse octree）结构中存储纹理数据。该方案非常适合交互式三维绘画系统，因为在创建时不需要为表面分配明确的纹理坐标，并且八叉树可以将纹理细节保持在所需的任何级别。Lefebvre 等。[1017] 讨论了在现代 GPU 上实现八叉树纹理的细节。Lefebvre 和 Hoppe [1018] 讨论了将稀疏体积数据打包为明显较小的纹理的方法。

 

6.2.4 立方体贴图 Cube Maps

另一类纹理是立方体纹理或立方体贴图，它具有六个方形纹理，每个纹理与一个立方体的一个面相关联。使用三分量纹理坐标向量访问立方体贴图，该向量指定了从立方体中心向外指向的光线的方向。光线与立方体相交的点如下。具有最大幅度的纹理坐标选择相应的面部（例如，向量（-3.2、5.1，-8.4）选择 -z 面部）。其余两个坐标除以最大幅度坐标的绝对值，即 8.4。它们现在的范围是 -1 到 1，并且只需将其重新映射到 [0，1] 即可计算纹理坐标。例如，坐标（-3.2，5.1）映射为（（-3.2 / 8.4 + 1）/ 2，（5.1 / 8.4 + 1）/ 2）≈（0.31，0.80）。多维数据集贴图用于表示作为方向函数的值； 它们最常用于环境映射（第10.4.3节）。

 

6.2.5 纹理表示 Texture Representation

处理应用程序中的许多纹理时，有几种提高性能的方法。纹理压缩在第 6.2.6 节中介绍，而本节的重点是纹理图集，纹理阵列和无绑定纹理，所有这些目的都是为了避免渲染时更改纹理造成的成本。在 19.10.1 和 19.10.2 节中，描述了纹理流和转码。

为了能够为 GPU 分配尽可能多的工作，通常最好更改状态的操作要尽可能少（第18.4.2节）。为此，可以将几张图像放在一个较大的纹理中，我们称为纹理图集。这在图 6.20 的左侧有说明。注意，子纹理的形状可以是任意的，如图 6.6 所示。Néoll 和 Stricker [1286] 描述了子纹理放置图集的优化。由于 mipmap 的上层可能包含几个单独的，不相关的形状，因此也需要注意 mipmap 的生成和访问。Manson 和 Schaefer [1119] 提出了一种通过考虑表面的参数化来优化 mipmap 创建的方法，该方法可以产生更好的结果。Burley 和 Lacewell [213] 提出了一个称为 Ptex 的系统，其中细分曲面中的每个四边形都有自己的小纹理。优点是，这避免了在网格上分配唯一的纹理坐标，并且在纹理图集的不连续部分的接缝处没有伪像（artifacts）。为了能够跨四边形进行滤波，Ptex 使用了邻接数据结构。当最初的目标是产品渲染时，Hillesland [746] 提出了打包的 Ptex（packed Ptex），它将每个面的子纹理放入纹理集，并使用相邻面的填充来避免滤波时的不连续性。Yuksel [1955] 提出了网格颜色纹理（mesh color textures），该纹理在 Ptex 上有所改进。Toth [1780] 通过实现一种方法，在滤波器抽头超出 [0，1] 的范围时将其丢弃，从而为类似 Ptex 的系统提供了跨表面的高质量滤波。

 图 6.20.  左：一个纹理图集，其中将九个较小的图像合成为一个大纹理。右：一种更现代的方法是将较小的图像设置为纹理数组，这是大多数 API 中都存在的概念。

 

使用图集的一个困难是包裹/重复和镜像模式，这不会作用到子纹理，而只会作用到整个纹理。为图集生成 mipmap 时，可能会发生另一个问题，其中一个子纹理会渗入另一个子纹理。但是，这可以通过在将每个子纹理放入大型纹理集之前分别为它们生成 mipmap 层次结构，并对子纹理使用 2 的幂次分辨率来避免这种情况 [1293]。

解决这些问题的一种更简单的解决方案是使用一种称为纹理数组（texture arrays） 的 API 构造，该构造完全避免了 mipmapping 和重复模式的所有问题 [452]。参见图 6.20 的右侧。纹理数组中的所有子纹理都必须具有相同的尺寸、格式、mipmap 层次结构和 MSAA 设置。就像纹理地图集一样，仅对纹理数组执行一次设置，然后就可以使用着色器中的索引访问任何数组元素。这比绑定每个子纹理 [452] 快 5 倍。

API 还支持无绑定纹理（bindless textures） [1407]，这也可以帮助避免状态更改的成本。如果没有无约束纹理，则使用 API 将纹理绑定到特定的纹理单元。其中一个问题是纹理单元数量的上限，这会使程序员感到麻烦。驱动程序确保纹理位于 GPU 侧。使用无绑定纹理时，纹理数量没有上限，因为每个纹理仅由一个 64 位指针（有时称为“句柄”，handle）与其数据结构相关联。可以通过许多不同方式来访问这些句柄，例如，通过 uniforms，通过变化的数据，来自其他纹理或从着色器存储缓冲区对象（SSBO）。应用程序需要确保纹理驻留在 GPU 端。无边界纹理避免了驱动程序中的任何类型的绑定成本，从而使渲染速度更快。

 

6.2.6 纹理压缩 Texture Compression

直接解决内存和带宽问题以及缓存问题的一种方案是固定比率纹理压缩（fifixed-rate texture compression） [127]。通过让 GPU 即时解码压缩的纹理，纹理可以需要更少的纹理内存，因此可以增加有效的缓存大小。至少同样重要的是，此类纹理的使用效率更高，因为它们在访问时消耗的内存带宽更少。一个相关但不同的用例是添加压缩以提供更大的纹理。例如，在  分辨率下每个纹理像素使用 3 字节的非压缩纹理将占用 768 kB。使用纹理压缩时，压缩比为6：1， 纹理将仅占用 512 kB。

图像文件格式（例如 JPEG 和 PNG）中使用了多种图像压缩方法，但是在硬件中对其进行解码的消耗是昂贵的（有关信息纹理的转码，请参见19.10.1节）。S3 开发了一种称为 S3 纹理压缩（S3 Texture Compression，S3TC）[1524] 的方案，该方案被选作 DirectX 的标准，并称为 DXTC。在 DirectX 10 中，它称为 BC（用于块压缩）。此外，它是 OpenGL 中的事实上的标准，因为几乎所有 GPU 都支持它。它具有创建大小固定的压缩图像的优点，压缩图像具有独立编码的片段，并且解码简单（因此快速）。图像的每个压缩部分都可以独立处理。没有共享的查找表或其他依赖项，从而简化了解码。

DXTC / BC 压缩方案有七个变体，它们具有一些共同的属性。编码是在 4×4 纹素块（也称为图块）上完成的。每个块分别编码。编码基于插值。对于每个编码量，存储两个参考值（例如，颜色）。将为该块中的 16 个纹理像素的每一个保存一个插值因子。它沿着两个参考值之间的直线选择一个值，即它等于或从两种存储的颜色进行插值的颜色。压缩来自仅存储两种颜色以及每个像素较短的索引值。

名字（Names）	存储（Storage）	参考颜色（Ref colors）	标记（Indices）	透明度（Alpha）	备注（Comment）
BC1 / DXT1	8 B / 4 bpt	RGB565 x 2	2 bpt	-	1 line
BC2 / DXT3	16 B / 8 bpt	RGB565 x 2	2 bpt	4 bpt raw	与 BC1 同颜色
BC3 / DXT5	16 B / 8 bpt	RGB565 x 2	2 bpt	3 bpt interp.	与 BC1 同颜色
BC4	8 B / 4 bpt	R8 x 2	3 bpt	-	1 channel
BC5	16 B / 8 bpt	RG88 x 2	2 x 3 bpt	-	2x BC4
BC6H	16 B / 8 bpt	见下文	见下文	-	针对 HDR；1-2 行
BC7	8 B / 4 bpt	见下文	见下文	可选	1-3 行

表6.1. 纹理压缩格式。所有这些压缩块均为4×4纹素。存储列显示每个块的字节数（B）和每个texel的位数（bpt）。参考颜色的表示法是首先是通道，然后是每个通道的位数。例如，RGB565 表示红色和蓝色为5位，而绿色通道为6位。

 

确切的编码在这七个变体之间有所不同，表 6.1 对此进行了总结。请注意，“ DXT” 表示 DirectX 9 中的名称，“ BC” 表示 DirectX 10 及更高版本中的名称。从表中可以看出，BC1具有两个16位参考RGB值（5位红色，6个绿色，5个蓝色），每个纹理像素具有 2 位插值因子，可以从参考值之一或两个中间值中进行选择。与未压缩的 24 位 RGB 纹理相比，这表示 6：1 的纹理压缩率。BC2 以与 BC1 相同的方式对颜色进行编码，但为量化（原始）alpha 值每纹理像素（bpt）添加4位。对于 BC3，每个块都有以与 DXT1 块相同的方式编码的 RGB 数据。此外，使用两个 8 位参考值和每个像素 3 位插值因子对 alpha 数据进行编码。每个纹理像素可以选择参考 alpha 值之一或六个中间值之一 (1)。BC4 具有一个通道，在 BC3 中编码为 alpha。BC5 包含两个通道，每个通道都像 BC3 中那样进行编码。

BC6H 用于高动态范围（HDR）纹理，其中每个纹理像素最初每个 R，G 和 B 通道具有 16 位浮点值。此模式使用 16 个字节，导致 8 bpt (?)。它具有用于单行的一种模式（类似于上述技术），以及用于两行的另一种模式，其中每块纹理可以从一小组分区中进行选择。两种参考颜色也可以进行增量编码以获得更高的精度，并且根据所使用的模式，它们也可以具有不同的精度。在 BC7 中，每个纹理块可以包含一到三行，并存储 8 bpt。我们的目标是 8 位 RGB 和 RGBA 纹理的高质量纹理压缩。它与 BC6H 共享许多属性，但是却是 LDR 纹理的格式，而 BC6H 是 HDR 的格式。请注意，在 OpenGL 中，BC6H 和 BC7 分别称为 BPTC FLOAT 和 BPTC。立方体或体积纹理以及二维纹理都可以应用这些压缩技术。

---

作者注：

(1) 备用 DXT1 模式为透明像素保留了四个可能的插值因子之一，从而将插值的数量限制为三个，即两个参考值及其平均值。

 

图 6.21. ETC（爱立信纹理压缩）对像素块的颜色进行编码，然后修改每个像素的亮度以创建最终的纹理像素颜色。（图像由JacobStr¨om压缩。）

 

这些压缩方案的主要缺点是它们是有损的。也就是说，通常无法从压缩版本中检索原始图像。对于 BC1 - BC5，仅使用四个或八个插值来表示 16 个像素。如果图块中包含更多数量的不同值，则会有一些损失。实际上，如果正确使用，这些压缩方案通常会提供可接受的图像保真度。

BC1 - BC5 的问题之一是，用于块的所有颜色都位于 RGB 空间中的直线上。例如，红色，绿色和蓝色不能在一个块中表示。BC6H 和 BC7 支持更多的线路，因此可以提供更高的质量。

对于 OpenGL ES，选择了另一种称为爱立信纹理压缩（Ericsson texture compression，ETC）[1714] 的压缩算法以包含在 API 中。该方案具有与 S3TC 相同的功能，即快速解码，随机访问，无间接查找和固定速率。它将 4×4 像素的块编码为 64 位，即每个纹理像素使用 4 位。基本思想如图 6.21 所示。每个 2×4 块（或 4×2 块，取决于提供最佳质量的块）都存储底色。每个块还从一个小的静态查找表中选择一组四个常量，并且块中的每个纹理像素都可以选择添加此表中的值之一。这种方法修改了每个像素的亮度。其图像质量与 DXTC 相当。

在 OpenGL ES 3.0 中包含的 ETC2 [1715] 中，未使用的位组合用于为原始的 ETC 算法添加更多模式。未使用的比特组合为压缩表示（例如 64 位），它被压缩为与另一压缩表示相同的图像。例如，在 BC1 中，将两个参考颜色设置为相同是没有用的，因为这将指示恒定的色块，只要一种参考颜色包含该恒定色，则可以依次获得该恒定色块。在 ETC 中，一种颜色也可以从第一种颜色加上带符号的数字进行增量编码，因此计算可能会上溢或下溢。这种情况被用来表示其他压缩模式。ETC2 添加了两个新模式，每个块具有四种颜色（以不同方式派生），而最终模式是 RGB 空间中的一个平面，用于处理平滑过渡。爱立信Alpha压缩（Ericsson alpha compression，EAC）[1868]用一个分量（例如 Alpha）压缩图像。这种压缩类似于基本的 ETC 压缩，但仅用于一个分量，并且结果图像的每个像素纹理存储 4 位。可以选择将其与ETC2组合使用，此外，可以使用两个 EAC 通道来压缩法线（有关此主题的更多信息，请参见下文）。所有的 ETC1，ETC2 和 EAC 都是 OpenGL 4.0 核心配置文件，OpenGL ES 3.0， Vulkan 和 Metal 的一部分。

压缩法线贴图（在第 6.7.2 节中讨论）时需要格外小心。专为 RGB 颜色设计的压缩格式通常无法正常显示 xyz 数据。大多数方法都利用这样的事实，即已知法线为单位长度，并进一步假定其 z 分量为正（正切空间法线的合理假设）。这仅允许存储法线的 x 和 y 分量。z 分量是动态导出的

由于仅存储两个分量，而不是三个，因此它本身会导致一定的压缩。由于大多数 GPU 本身并不支持三分量纹理，因此这也避免了浪费分量的可能性（或必须在第四分量中打包其他数量的分量）。通常，通过将 x 和 y 分量存储在BC5 / 3Dc格式纹理中，可以实现进一步的压缩。参见图 6.22。由于每块的参考值划分了最小和最大 x 和 y 分量值，因此可以将它们视为在 xy 平面上定义边界框。三位插值因子允许在每个轴上选择八个值，因此会将边界框划分为 8×8 的可能的法线网格。或者，可以使用 EAC 的两个通道（用于 x 和 y），然后按照上面的定义计算 z。

 

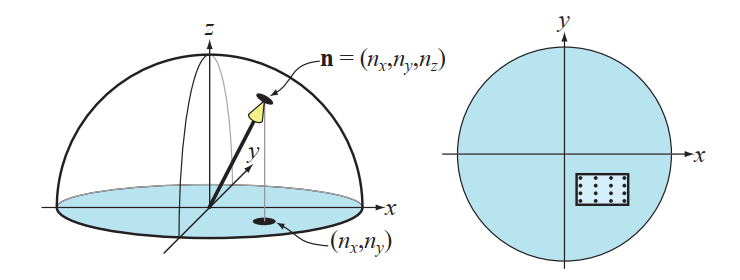
图 6.22. 左：球体上的法线单位只需要编码 x 和 y 分量。右：对于 BC4 / 3Dc，xy 平面中的一个框将法线围起来，每 4×4 个法线块可在此框内使用 8×8 个法线（为清楚起见，此处仅显示 4×4 个法线）。

 

在不支持 BC5 / 3Dc 或 EAC 格式的硬件上，常见的回退（fallback） [1227] 是使用 DXT5 格式的纹理并将两个分量存储在绿色和 alpha 分量中（因为这些分量的存储精度最高） 。其他两个分量未使用。

PVRTC [465] 是 Imagination Technologies 研发的在名为 PowerVR 的硬件上可用的纹理压缩格式，其最广泛的用途是用于 iPhone 和 iPad。它为每个纹理像素提供 2 位和 4 位的方案，并压缩 4×4 纹理像素的块。其关键思想是提供图像的两个低频（平滑）信号，这些信号是使用相邻的像素数据块进行插值获得的。然后，每个纹理像素使用 1 或 2 位在图像上的两个信号之间进行插值。

自适应可伸缩纹理压缩（Adaptive scalable texture compression，ASTC）[1302] 的不同之处在于，它将 n×m 纹理像素的块压缩为 128 位。块大小从 4×4 到 12×12 不等，这导致了不同的比特率，从每纹理像素低至 0.89 位到每纹理像素高达 8 位。ASTC 使用多种技巧来实现紧凑的索引表示，并且每个块都可以选择行数和端点编码。此外，ASTC 可以处理每个纹理 1 至 4 个通道以及 LDR 和 HDR 纹理。ASTC 是 OpenGL ES 3.2 及更高版本的一部分。

上面介绍的所有纹理压缩方案都是有损的，并且在压缩纹理时，可以选择在此过程上花费不同的时间。可以花几秒钟甚至几分钟来进行压缩，以获得更高的质量。因此，该过程通常是作为脱机预处理完成的，并且会存储起来供以后使用。另外，如果只花费几毫秒的时间压缩，那结果的质量会较低，但是这样的话纹理可以实时压缩并立即使用。关于实时压缩的一个例子是天空盒（第13.3节），每隔一秒左右就会重新生成一次，此时云层可能已经略微移动了。由于解压缩是使用固定功能的硬件完成的，因此该过程的速度非常快。其中压缩的过程会并且确实比解压缩花费更长的时间，这种差异称为数据压缩不对称（data compression
asymmetry）。

Kaplanyan [856]提出了几种可以改善压缩纹理质量的方法。对于包含颜色的纹理和法线贴图，建议使用每个分量 16 位的方式创作贴图。对于彩色纹理，执行直方图重归一化（histogram renormalization）（在这16位上），然后使用着色器中的比例和偏置常数（每个纹理）反转其效果。直方图归一化是一种将图像中使用的值扩展到整个范围的技术，这实际上是一种对比度增强。每个分量使用 16 位可确保在重新归一化后直方图中没有闲置的时隙，这减少了许多纹理压缩方案可能引入的条带失真。如图 6.23 所示。此外，如果75％的像素高于116/255，Kaplanyan建议对纹理使用线性颜色空间，否则将纹理存储在sRGB中。对于法线贴图，他还指出BC5 / 3Dc通常独立于y来压缩x，这意味着并非总能找到最佳法线。相反，他建议对法线使用以下错误度量：

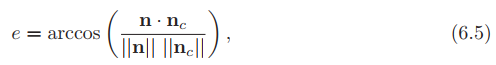
其中 是原始法线， 是相同的法线压缩，然后解压缩。

图 6.23. 每个分量使用 16 位的效果，而纹理压缩时使用 8 位的效果。从左到右：原始纹理，DXT1 从每个分量 8 位压缩，DXT1 从每个分量 16 位压缩，并在着色器中进行了重新归一化。为了更清楚地显示效果，已在强光下渲染了纹理。（图片由 Anton Kaplanyan 提供。）

 

应当注意，还可以在不同的颜色空间中压缩纹理，这可以用来加速纹理压缩。常用的变换是 [1112]：

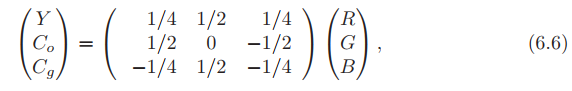
其中， 是亮度项， 和  是色度项。逆变换的消耗也并不昂贵：

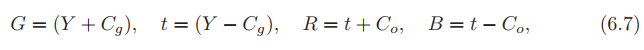
这仅仅相当于做了几次加法。可以从公式 6.6 中看出，这两个变换是线性的，它是矩阵向量乘法，其本身即是线性的（请参见公式 4.1 和 4.2）。这一点很重要，因为我们可以存储 ，而不是将 RGB 存储在纹理中。纹理处理器仍然可以在  空间中执行滤波，然后像素着色器可以根据需要转换回 RGB。应该注意的是，这种变换本身是有损的，这可能会有问题，也可能不会。(?)

还有另一个可逆的  变换，可以总结为

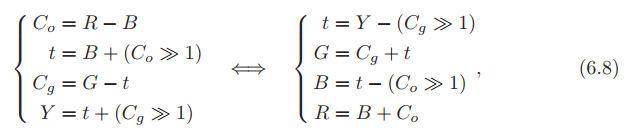
符号 ≫ 为右移运算。(?)这里的意思是可以在例如 24 位 RGB 颜色和相应的 表示之间进行来回转换而不会造成任何损失。应该注意的是，如果 RGB 中的每个分量都具有 n 位，则  和  均具有 n +1 位，以确保可逆变换。 虽然只需要 n 位。Van Waveren 和 Casta〜no [1852] 使用有损  变换在 CPU 或 GPU 上实现对 DXT5 / BC3 的快速压缩。它们将  存储在 alpha 通道中（因为它具有最高的精度），而 和 存储在 RGB 的前两个分量中。由于  分别存储和压缩，因此压缩变得很快。对于  和 组分，他们找到一个二维边界框，并选择产生最佳结果的对角线框。请注意，对于在 CPU 上动态创建的纹理，最好也压缩 CPU 上的纹理。通过在 GPU 上渲染来创建纹理时，通常最好也压缩 GPU 上的纹理。 变换和其他亮度色度变换通常用于图像压缩，其中色度分量在 2×2 像素上平均。这样可将存储量减少 50％，并且由于色度趋于缓慢变化，因此通常可以正常工作。Lee-Steere 和 Harmon [1015] 通过将其转换为色相饱和度值（HSV），将色相和饱和度下采样 x 和 y 的系数为 4，并将值存储为单通道 DXT1 纹理，从而更进一步。Van Waveren 和 Casta〜no 也描述了法线图压缩的快速方法 [1853]。

Griffin 和 Olano [601] 的研究表明，将多个纹理应用于具有复杂着色模型的几何模型时，纹理的质量通常可以很低，但却不会有明显的视觉差异。因此，根据使用情况，降低质量是可以接受的。Fauconneau [463] 提出了 DirectX 11 纹理压缩格式的 SIMD 实现。

 

6.3 程序纹理 Procedural Texturing

给定纹理空间位置，执行图像查找是生成纹理值的一种方法。另一个办法是计算一个函数，从而产生程序纹理（procedural texture）。

尽管程序纹理通常在脱机渲染的应用程序中使用，而图像纹理在实时渲染中更为常见。但这是由于现代 GPU 中图像纹理化硬件的极高效率造成的，它可以在一秒钟内执行数十亿次纹理访问。但是，GPU 体系结构正在朝着更低廉的计算和（相对）更昂贵的内存访问发展。这些趋势已使程序纹理在实时应用程序中得到了更多的使用。

考虑到体积图像纹理的高昂的存储成本，体积纹理对于程序纹理方法来说特别有吸引力。我们可以通过多种技术来合成这样的纹理。最常见的方法之一是使用一个或多个噪声函数来生成值 [407、1370、1371、1372] 。参见图 6.24。噪声函数通常在两个连续的二次方频率（称为八度，octaves）上采样。每个八度都有权重，通常随着频率的增加而降低，这些加权样本的总和称为湍流函数（turbulence function）。

图 6.24. 使用体积纹理进行实时程序纹理化的两个示例。左侧的大理石是使用光线步进（ray marching）渲染的半透明体积纹理。在右侧，该对象是使用复杂的程序木质着色器 [1054] 生成并在现实环境中合成的合成图像。（左图来自 Shadertoy 的“Playing marble”，由圣安妮·古利特（St´ephane Guillitte 提供）。右图由 Autodesk，Inc.的尼古拉斯·萨瓦（Nicolas Savva）提供。

 

由于计算噪声函数的成本，通常会预先计算三维阵列中的晶格点，并将其用于内插纹理值。有多种使用颜色缓冲区混合来快速生成这些数组的方法 [1192]。Perlin [1373] 提出了一种快速，实用的方法来对该噪声函数进行采样，并展示了一些用途。Olano [1319] 提供了噪声生成算法，允许在存储纹理和执行计算之间进行权衡。McEwan等。[1168] 开发了无需任何查找即可在着色器中计算经典噪声（classic noise）和 Simplex 噪声（simplex noise）的方法，并且提供了源代码。Parberry [1353] 使用动态编程在多个像素上摊销计算，以加快噪声计算。Green [587] 提供了一种更高质量的方法，但是对于接近交互的应用程序，它意味着更多的方法，因为它使用 50 像素着色器指令进行一次查找(?)。Perlin [1370，1371，1372] 提出的原始噪声函数可以进行改进。Cook 和 DeRose [290] 提出了另一种表示形式，称为小波噪声，它避免了走样问题，而评估成本仅增加了一点点。Liu 等。[1054] 使用各种噪声函数来模拟不同的木材纹理和表面光洁度。另外，我们还推荐阅读 Lagae 等人 [956] 关于该话题的最新报告。

其他程序化方法也是可行的。例如，通过测量从每个位置到散布在空间中的一组“特征点”之间的距离来形成细胞纹理。以各种方式（例如更改颜色或着色法线）映射所得到的最接近距离，可以创建一些看起来像细胞，石板，蜥蜴皮和其他自然纹理的图案。Griffiths [602] 讨论了如何有效地找到最近邻并在 GPU 上生成蜂窝状纹理。

程序纹理的另一种类型是物理模拟或其他交互过程的结果，例如水波纹或扩展裂缝。在这种情况下，程序纹理可以对动态条件做出有效的、无限的变化。

当生成程序化二维纹理时，参数化问题可能比创作的纹理面临更大的困难，在创作的纹理中，可以手动修改或解决拉伸或接缝伪像。一种解决方案是通过将纹理直接合成到表面上来完全避免参数化。在复杂的表面上执行此操作在技术上具有挑战性，并且是研究的活跃领域。有关该领域的概述，请参见 Wei 等人的文章 [1861]。

反走样的程序纹理与反走样的图像纹理相比既困难又容易。一方面，诸如 mipmapping 之类的预计算方法不可用，这给程序员带来了负担。另一方面，程序纹理的开发者具有有关纹理内容的“内部信息”，因此可以对其进行调整以避免走样。对于通过对多个噪声函数求和而创建的程序纹理尤其如此。每个噪声函数的频率都是已知的，因此可以丢弃任何会引起走样的频率，从而在实际上降低了计算成本。有多种技术可以消除其他类型的程序纹理的锯齿 [407、605、1392、1512]。Dorn 等人 [371] 讨论了先前的工作，并提出了一些用于重新构造纹理函数以避免高频（即被频带限制，band-limited）的过程。

最后

以上就是眯眯眼歌曲为你收集整理的《Real-Time Rendering 4th Edition》全文翻译 - 第6章 纹理化（上）6.1 ~ 6.3实时渲染（第四版）Real-Time Rendering (Fourth Edition)第6章 纹理化 Chapter 6 Texturing的全部内容，希望文章能够帮你解决《Real-Time Rendering 4th Edition》全文翻译 - 第6章 纹理化（上）6.1 ~ 6.3实时渲染（第四版）Real-Time Rendering (Fourth Edition)第6章 纹理化 Chapter 6 Texturing所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。