牛客寒假算法基础集训营2 非官方题解

72 阅读 0 评论 48 点赞

我是靠谱客的博主贤惠猫咪，最近开发中收集的这篇文章主要介绍牛客寒假算法基础集训营2 非官方题解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

emmmm今天看到群里有人发题解…然后我自己也想写一个…毕竟自己写的题…拿来装装逼也是可以的吧xixixixixi

A 处女座的签到题

链接：https://ac.nowcoder.com/acm/contest/327/A
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述
平面上有n个点，问：平面上所有三角形面积第k大的三角形的面积是多少?

输入描述:
第一行T，表示样例的个数。
对于每一组样例，第一行两个整数n和k，
接下来n行，每行两个整数x,y表示点的坐标

T<=80
3<=n<=100
-109<=x,y<=109
对于每一组样例，保证任意两点不重合，且能构成的三角形的个数不小于k

输出描述:
对于每一组样例，输出第k大三角形的面积，精确到小数点后两位（四舍五入）。

示例1

输入
1
4 3
1 1
0 0
0 1
0 -1

输出
0.50

说明
样例中一共能构成3个三角形，面积分别为0.5，0.5，和1，面积第3大的为0.5

题目n很小,只有100,所以可以直接暴力 $O(n^3)$ 枚举三角形的每个点，并把每个三角形的面积存下来
已知三点坐标求三角形面积有公式：
$S=frac{1}{2}(x_1*y_2+x_2*y_3+x_3*y_1-x_1*y_3-x_2*y_1-x_3*y_2)$
这个公式求出来的面积有正负，因为在平面直角坐标系中我们认为逆时针面积为正，顺时针为负。

就算不知道这个公式，也可以采用另一个公式。我们知道两个向量的叉乘的数值代表的是以这两个向量为邻边的平行四边形的面积，而三角形的面积是平行四边形的一半，也就是说三角形的面积是
$S = 1 2 A B ⃗ × A C ⃗ S=frac{1}{2} vec{AB} times vec{AC}$
向量直接用两点坐标相减就可以了，这个就不详细讲了

再补充一下精度的问题，通过上面给出的两个公式，显然结果都是1/2乘一个整数，所以小数部分要么是0.50要么是0.00
题目给的点坐标的数据范围在1e9，所以要算面积的时候乘法会炸int，所以要开long long，而long long在转换为double的时候会有两位的精度丢失（double的绝对有效位数只有15位，第16位开始可能会有偏差，尽管double能表示的最大的数在1e305这个数量级），所以我没考虑用double，直接算面积的2倍，最后输出的时候再除2，小数部分特判

问题在于，把所有的三角形面积求出来之后，怎么求出第k大的面积
这题的坑点就是，如果通过排序再取第k大，复杂度为 $O (n l o g n)$

严格来说，这里的n最大为100，三角形的个数为 $O(n^3)$ ，所以排序再取第k大的复杂度是 $O(n^3log(n^3))$ ，大概可以估计到这个数大概1e7这个数量级的。（或者你也可以说 $C_{n}^{3}$ 是三角形个数，但是数量级算出来差不多），然后题目中说最多有80组数据，所以估计复杂度量级超过了1e8，这个复杂度能不能过就要看命了。而这题确实也卡了这个复杂度，所以 $O (n l o g n)$ 求第k大会TLE

事实上，对于求第k大的数，有一个库函数，nth_element。具体函数说明参见下图
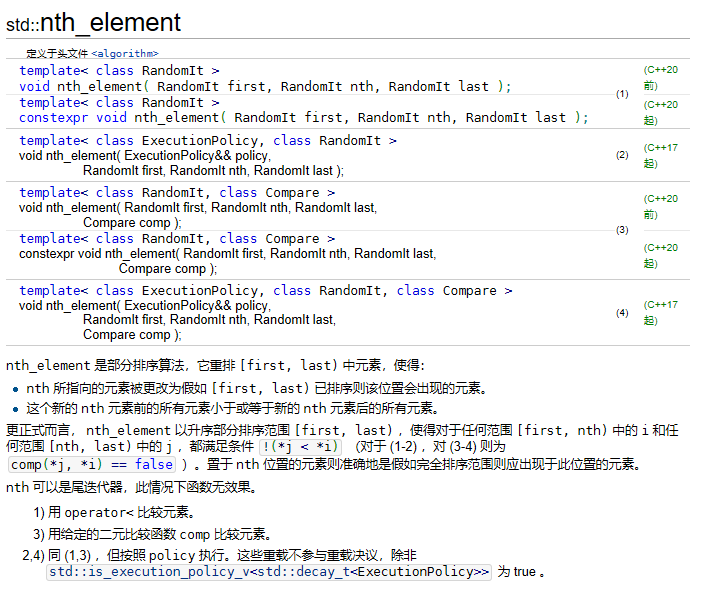
在这里插入图片描述
这个函数能对一个序列进行部分排序，最终保证第k个位置的数在正确排好序的位置上，函数实现的复杂度为 $O (n)$ ，刚好满足这个题目的需要

那么这个题的各种细节讲到这里就结束了，最后上我的代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 105;
long long x[maxn], y[maxn];
long long S[1000000];
long long getS(int i, int j, int k) {
    return x[i]*y[j]+x[j]*y[k]+x[k]*y[i]-x[i]*y[k]-x[j]*y[i]-x[k]*y[j];
}
int main() {
    int T; scanf("%d", &T);
    while(T--) {
        int n, K; scanf("%d%d", &n, &K);
        for(int i = 1; i <= n; i++) scanf("%lld%lld", &x[i], &y[i]);
        int idx = 0;
        for(int i = 1; i <= n; i++)
            for(int j = i+1; j <= n; j++)
                for(int k = j+1; k <= n; k++) {
                    if((x[j]-x[i])*(y[k]-y[j]) == (y[j]-y[i])*(x[k]-x[j]))
                        continue;
                    long long s = getS(i, j, k);
                    if(s < 0) s = -s;
                    if(s) S[idx++] = s;
                }
        K = idx-K;
        nth_element(S, S+K, S+idx);
        long long ans = S[K];
        printf("%lld", ans>>1);
        printf(ans&1 ? ".50n" : ".00n");
    }
    return 0;
}

B 处女座与cf

链接：https://ac.nowcoder.com/acm/contest/327/B
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述
众所周知，处女座经常通过打cf来调节自己的心情。今天处女座又参加了一场cf的比赛，他知道了所有的提交记录，他想知道自己的得分和排在第几名。你知道处女座的cf账号是cnz
Codeforces规则如下：
1.比赛一共2小时
2.比赛有5题，A题500分，B题1000分，C题1500分，D题2000分，E题2500分。
3.得分规则如下：
在第0分钟完成某一题可以得到全部的分数，每过一分钟每题的分值会衰减1/250，比如在第3分钟完成A题，能够得到500-23=494分
4.如果一道题是的返回结果WA或者TLE被称为错误的提交，CE视为无效的提交，AC，WA和TLE 都视为有效的提交。如果一道题你最后通过了，你会得到这道题衰减之后的分值再减去你错误提交次数50，就是每次错误的提交会有50分的罚时。
5.如果你通过了一道题，你的得分不会低于该题分值的30%。比如你在第50分钟通过了A，你有7次错误的提交，你的得分为max(5000.3,500-250(得分衰减)-7*50(错误提交的罚时))=150分。
6.由于hack机制的存在，你每进行一次提交，对于这一题之前的有效提交(AC,WA,TLE)都视为错误的提交。
7.一个人只有提交(AC,WA,TLE,CE)过代码，才被视为参加比赛。
处女座又了解到一些信息：
本场比赛没有任何选手hack别人，并且没有任何的提交fst（即只要是某题的最后一次提交通过，就视为通过这道题）

输入描述:
第一行两个整数n和m，n为报名比赛的人数，m为提交的个数
接下来n行，每行一个字符串，表示报名比赛的人的昵称。（字符串只包含小写字母，且长度小于20）
接下来m行，每行的格式为Time，Submiter，Problem，Verdict。
Time为提交的时间，是1到120中的一个正整数（包含1和120）,保证Time按顺序给出
Submiter为提交者昵称
Problem为题目名称，是’A’,’B’,’C’,’D’,’E’中的一个字母。
Verdict为返回的结果，为”AC”,”WA”,”TLE”,”CE”中的一个。

2<=n<=500
1<=m<=10000

输出描述:
如果处女座参加了比赛,输出两行:
第一行为处女座的得分
第二行格式x/y,其中x为处女座的排名，y为参加比赛的总人数。如果分数相同那么排名并列。
如果处女座没有参加比赛，输出”-1”

示例1

输入
3 7
cnz
cuber
moon
3 cnz A AC
5 cuber A AC
6 cnz B CE
10 cuber C AC
20 cnz B AC
30 cuber D TLE
100 cnz E AC

输出
2914
1/2

这题纯模拟，没什么好说的细节，只能是题目中几个点：

如果在AC之后再次提交，结果出现WA，TLE，甚至包括CE，则这题之前的AC算错误，如果之后没有出现AC，则这题不计分
同分时排名并列，之后的排名顺延，即：如果有10个最高分，那么次高分是第十一名而不是第二名

除了这两点我就不知道还有没有对题目理解上的歧义了，剩下的直接上代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 505;
const int maxm = 10005;
map<string, int> mpID;
bool attended[maxn];//attended[i]表示第i个人是否参加比赛
int submitCnt[maxn][10];//submitCnt[i][j]表示第i个人第j题的提交次数
int lastAC[maxn][10];//lastAC[i][j]表示第i个人通过第j题的时间
int score[maxn];//score[i]表示第i个人的最终得分
int main() {
    mpID.clear();
    memset(attended, 0, sizeof(attended));
    memset(submitCnt, 0, sizeof(submitCnt));
    memset(lastAC, -1, sizeof(lastAC));
    memset(score, 0, sizeof(score));
    int n, m; cin>>n>>m;
    for(int i = 1; i <= n; i++) {
        string name; cin>>name;
        mpID[name] = i;
    }
    memset(attended, 0, sizeof(attended));
    int attendCnt = 0;
    while(m--) {
        int time;
        string submiter, problem, verdict;
        cin>>time>>submiter>>problem>>verdict;
        int ID = mpID[submiter];
        int problemID = problem[0] - 'A' + 1;
         
        if(!attended[ID]) attended[ID] = 1, attendCnt++;//参赛人数
        if(verdict.compare("CE") == 0)//无效的提交
            lastAC[ID][problemID] = -1;//未通过，覆盖前面的时间
        else {
            submitCnt[ID][problemID]++;//该题提交次数+1
            if(verdict.compare("AC") == 0)//通过这题，记录时间
                lastAC[ID][problemID] = time;
            else lastAC[ID][problemID] = -1;//未通过，覆盖前面的时间
        }
    }
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= 5; j++)
            if(lastAC[i][j] != -1)
                score[i] += max(150*j, 500*j - 2*j*lastAC[i][j] - 50*submitCnt[i][j]+50);
    int userID = mpID["cnz"];
    if(!attended[userID]) {
        cout<<-1<<endl;
        return 0;
    }
    cout<<score[userID]<<endl;
    int rank = 1;
    for(int i = 1; i <= n; i++)
        if(score[i] > score[userID]) rank++;
    cout<<rank<<"/"<<attendCnt<<endl;
    return 0;
}

作为一个不擅长写模拟题的选手的个人经验，模拟题一定要先理清思路再动手，如果思路不是百分百清晰，那么写的时候一定要注意变量命名和注释。（嗯我就是在吐槽std的代码丝毫没有可读性）
所以我觉得我这份代码还是挺emmmm优秀的吧（至少我觉得比std更适合当std略略略）

C 处女座的砝码

链接：https://ac.nowcoder.com/acm/contest/327/C
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述
处女座热爱做物理实验，为了实验，处女座必须要精确的知道物品的质量。处女座准备自己设计一套砝码，每一个砝码都是正整数，这套砝码必须能够精确测量出n以内所有正整数的质量，处女座想要知道至少需要多少个砝码。你可以在天平的任意一边放置砝码。

输入描述:
一行，一个正整数n

1<=n<=101000

输出描述:
一个整数，表示最少的砝码数。
示例1

输入
20

输出
4

说明
你可以选择1，2，6，11
1=1
2=2
3=1+2
4=6-2
5=6-1
6=6
7=6+1
8=6+2
9=6+2+1
10=11-1
11=11
12=11+1
13=11+2
14=11+2+1
15=11+6-2
16=11+6-1
17=11+6
18=11+6+1
19=11+6+2
20=11+6+2+1

这题是需要找一点规律的，假设前 $i$ 个砝码可以表示的最多的重量为 $a_i$ （这句话的意思是用前i个砝码，能测量出1到 $a_i$ 中任意正整数的质量）
显然有 $a_1=1$
假设已知 $a_i$ ，那么要加入下一个砝码，可以想到下一个砝码的质量为 $2a_i+1$ （不要问我怎么想到的，我也不知道怎么想到的，反正就是想到了），因为这样， $a_i$ 之前的数用前i个砝码即可表示，如果将新的砝码放入天平左侧，通过将前 $i$ 个砝码（有选择性的）和待称物品放到右侧，可以在右侧测出 $a_i$ 到 $2a_i+1$ 中的任意整数，如果将新的砝码和原来的前 $i$ 个砝码放到天平左侧，就能在右侧测出 $2a_i+1$ 到 $3a_i+1$ 中的任意整数。
从而此时能表示的最大的整数，即 $a_{i+1}$ 的值为 $3a_i+1$ ，即 $a_{i+1}=3a_i+1$
由数列知识可得 $a_n+0.5=1.5times3^{n-1}$ ，即 $a_n=frac{3^n-1}{2}$ ，这里 $a_n$ 表示的是用n个砝码能表示出的最大质量
题目中要求的是n，所以将n提出来之后变成 $n={log_3 {(2a_n+1)}}$
只要将输入的数当做 $a_n$ ，然后对等式右边取上界得到的n即为结果
大数用python或java，嗯

import math
a = int(input())
a = math.log(a*2 + 1, 3)
if(a-int(a) > 0):
    a += 1;
print(int(a))

D 处女座与重修费

链接：https://ac.nowcoder.com/acm/contest/327/D
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述
期末考试结束了，处女座发现很多人挂了大物，只能等着第二年重修，还要交400元的重修费。处女座突然想起有个学长和他讲过，如果学校哪一年缺钱了，那一年的大物试卷就会特别难。现在处女座有了所有人的成绩，处女座想知道如果所有挂科的人都在第二年重修，学校能赚多少重修费？
挂科是指一门课的分数小于60分。

输入描述:
第一行一个整数n，表示考试的人数。
第二行n个整数，表示每个人的成绩。

1<=n<=10000
学生的成绩为0-100（包括0和100）之间的整数

输出描述:
一行，学校能赚的重修费用

示例1

输入
4
60
56
100
59

输出
800

这个签到题emmmm不会的话重新回去从语言学起吧

#include<bits/stdc++.h>
using namespace std;
int main() {
    int n; scanf("%d", &n);
    int cnt = 0;
    while(n--) {
        int t; scanf("%d", &t);
        if(t < 60) cnt += 400;
    }
    printf("%dn", cnt);
    return 0;
}

E 处女座与汉明距离

没做
留题面（因为不写题解所以就不排版了）
链接：https://ac.nowcoder.com/acm/contest/327/E
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
Special Judge, 64bit IO Format: %lld
题目描述
定义两个数之间的汉明距离为两个数异或值的二进制中1的个数。
问是否存在一个0-2n-1的排列a，使得相邻两个数ai和ai+1的汉明距离均为m，
a
2
n
a2n和a1也算相邻。
输入描述:
一行，两个数n和m
2<=n<=20, 1<=m<n
输出描述:
如果存在这样的排列，第一行输出"YES",下面2n行，每行一个整数，输出这个排列。如果有多组答案，输出任意一组即可
如果不存在，输出”NO”
示例1
输入
2 1
输出
YES
0
1
3
2

F 处女座与宝藏

没做
留题面（因为不写题解所以就不排版了）
链接：https://ac.nowcoder.com/acm/contest/327/F
来源：牛客网

时间限制：C/C++ 2秒，其他语言4秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld
题目描述
处女座进行了一次探险，发现了一批宝藏。如果他获得这批宝藏，那么他一辈子都不需要工作了。但是处女座遇到了一个难题。
宝藏被装在n个宝箱里，宝箱编号为1,2,…,n，只有所有宝箱在某一时间被打开，处女座才能获得宝藏。有m个开关，每个开关控制k个宝箱，如果按下一个开关，那么这k个宝箱的开关状态都会发生改变（从开启变成关闭，从关闭变成开启），处女座想知道他能否获得这批宝藏。
输入描述:
第一行两个正整数n,m，
第二行n个整数，每个整数为0或1，表示初始时宝箱的状态，0表示开启，1表示关闭
接下来m行，每行开头一个整数k表示这个开关控制的宝箱的个数，接下来k个整数，表示控制宝箱的编号
1<=n,m<=200000
1<=k<=n
题目保证每个宝箱最多被两个开关控制。
输出描述:
一行，如果处女座能获得宝藏，输出”YES”，否则输出”NO”
示例1
输入
4 4
1 0 1 1
2 3 4
2 1 3
1 2
2 1 2
输出
YES

G 处女座与复读机

链接：https://ac.nowcoder.com/acm/contest/327/G
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述
一天，处女座在牛客算法群里发了一句“我好强啊”，引起无数的复读，可是处女座发现复读之后变成了“处女座好强啊”。处女座经过调查发现群里的复读机都是失真的复读机，会固定的产生两个错误。一个错误可以是下面的形式之一：
1.将任意一个小写字母替换成另外一个小写字母
2.在任意位置添加一个小写字母
3.删除任意一个字母
处女座现在在群里发了一句话，他收到了一个回应，他想知道这是不是一个复读机。

输入描述:
两行
第一行是处女座说的话s
第二行是收到的回应t

s和t只由小写字母构成且长度小于100

输出描述:
如果这可能是一个复读机输出”YES”，否则输出”NO”

示例1

输入
abc
abcde

输出
YES

说明
abc->abcd->abcde

示例2

输入
abcde
abcde

输出
YES

说明
abcde->abcdd->abcde

备注:
只要能经过两步变换就从s得到t就有可能是复读机

惭愧。。。这题是一个经典题的弱化版。原题是给出s和t，问从s变换到t的最小操作次数。
原题的思路我记得，但是代码比赛的时候死活写不出来。。。所以既然是个弱化版的题，我就给了个弱化版的代码。
在这里还是先讲原题的思路吧。原题是个动态规划问题，用 $d p [i] [j]$ 表示 $s [0 . . i]$ （表示s[0]到s[i]构成的子串）变换到 $t [0 . . j]$ 所需要的变换次数
如果s[i]和t[j]相等，那么 $d p [i] [j] = d p [i + 1] [j + 1]$ ，否则，进行分类讨论：

如果t[j]是原串中的字符采取替换字符的操作变成的，那么 $d p [i] [j] = d p [i + 1] [j + 1] + 1$
如果t[j]是原串中的字符采取删除字符的操作变成的，那么 $d p [i] [j] = d p [i + 1] [j] + 1$
如果t[j]是原串中的字符采取添加字符的操作变成的，那么 $d p [i] [j] = d p [i] [j + 1] + 1$

所以状态转移方程为：
若 $s [i] = t [j]$ ，则 $d p [i] [j] = d p [i + 1] [j + 1]$
否则 $d p [i] [j] = m i n (d p [i + 1] [j + 1], d p [i + 1] [j], d p [i] [j + 1]) + 1$

放在这题中只需要判断 $d p [n] [m] \leq 2$ 是否成立就行了（这里n和m分别表示两个字符串的长度）
有人纠结为什么只要小于等于2就行了，如果等于1或0那怎么办呢？

等于0很简单，先将第1个字符变成其他字符，再变回来，就是2次复读机操作
等于1的话，可以先做一次没用的操作，再做这个操作。比如说abc->abcd，最少只需要1次操作，为了凑足2次操作，可以先做一个没用的操作，即abc->abce->abcd

嗯这应该才是这题的正解，然而比赛的时候我并没有采取这种写法。这个写法又臭又长，但是基本思路其实跟上面的dp差不多的。如果能理解dp的话再看我的代码应该也不难懂。

因为代码比较丑，解释起来比较麻烦，就不解释了

#include<bits/stdc++.h>
using namespace std;
const int maxn = 105;
char s[maxn], t[maxn];
bool mark[maxn][maxn][3];
bool dfs(int i, int j, int op) {
    if(i == -1 && j == -1) return op == 0 || op == 2;
    if(i == -1) return op == j+1;
    if(j == -1) return op == i+1;
    if(mark[i][j][op]) return true;
    if(s[i] != t[j]) {
        if(op == 0) return false;
        if(dfs(i-1, j-1, op-1)) return mark[i][j][op] = true;//替换
        if(dfs(i, j-1, op-1)) return mark[i][j][op] = true;//添加
        if(dfs(i-1, j, op-1)) return mark[i][j][op] = true;//删除
        return false;
    }
    return mark[i][j][op] = dfs(i-1, j-1, op);
}
int main() {
    memset(mark, 0, sizeof(mark));
    scanf("%s%s", s, t);
    int ls = strlen(s), lt = strlen(t);
    printf(dfs(ls-1, lt-1, 2) ? "YESn" : "NOn");
    return 0;
}

H 处女座的测验（一）

链接：https://ac.nowcoder.com/acm/contest/327/H?&headNav=acm
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
Special Judge, 64bit IO Format: %lld

题目描述
处女座进行了一场c语言的考试，要求很简单，输出2000个正整数，并且满足以下条件：
1.任意两个数互质
2.任意两个数x,y，满足 $τ (x \cdot y) > 10$ ，其中为n的因子的个数
举例：6的因子有1，2，3，6，所以τ(6)=4

输入描述:
本题没有输入

输出描述:
2000行，每行一个正整数
输出的每个整数都必须在 $1-4times10^8$ 之间
如果有多组答案，输出任意一组即可。

要求任意两个数互质，很容易想到任意两个质数都互质，且任意一个质数都只能作为2000个数中至多一个数的因子
要求任意两个因子的乘积有超过10个因子，有一个显而易见的结论：如果A和B互质，且A有p个因子，B有q个因子，则他们的乘积AB有pq个因子。因为题中任意两个数互质，所以只要保证每个数都有4个因子即可。而因子会包括1和本身，所以只要有另外的两个因子即可
一种构造方法是找出前2000个素数，然后对第 $i$ 个素数 $p_i$ 构造 $p_i^3$ 。但可以发现，这个构造方法不满足题目要求的4e8的范围
另一种办法是找出前4000个素数，然后构造第i个数为相邻的第i对素数的乘积。这样也会超出范围
在想过前两种构造方法之后，很容易想到的构造方法是，找出前4000个素数，构造第 $i$ 个数为 $p r i m e [i] * p r i m e [4001 - i]$ 。这个方法满足题意，因为数的数量不多，我是直接在本地跑出来然后直接交的。理论上在交的代码中跑应该也能过。

#include<bits/stdc++.h>
using namespace std;
int a[2000] = {75626, 113433, 188995, 264481, 415591, 490711, 641189, 716281, 866939, 1093039, 1167553, 1393309, 1543609, 1618649, 1768751, 1993807, 2218813, 2293051, 2518463, 2668109, 2742829, 2968109, 3118061, 3342929, 3642253, 3792247, 3866311, 4015603, 4089353, 4238743, 4763389, 4912631, 5136541, 5210971, 5584967, 5656913, 5879179, 6102883, 6249641, 6471757, 6694063, 6765599, 7137479, 7211059, 7360117, 7434043, 7878529, 8326151, 8471867, 8544677, 8692997, 8916373, 8983757, 9355523, 9574021, 9794909, 10012987, 10085807, 10304677, 10452919, 10524487, 10894033, 11411497, 11556449, 11624507, 11767991, 12285727, 12501689, 12869189, 12934289, 13081121, 13300591, 13593313, 13808833, 14030201, 14175979, 14394167, 14687809, 14828579, 15121957, 15480793, 15553003, 15917261, 15990257, 16209197, 16355117, 16573937, 16863757, 17010439, 17078681, 17221559, 17661209, 17949359, 18091877, 18379667, 18520963, 18735781, 19169153, 19241693, 19901767, 20119207, 20485903, 20699821, 20917009, 20983679, 21198403, 21555227, 21770809, 21988691, 22054897, 22271437, 22486679, 22629709, 22699349, 23128043, 23488163, 23557591, 23698963, 23904371, 24118741, 24184007, 24620359, 24758567, 24972529, 25262269, 25622251, 25907569, 26264351, 26555129, 26771359, 26971283, 27114299, 27395729, 27610061, 27752909, 28043123, 28181261, 28686937, 29037101, 29438701, 29506613, 29862233, 29918519, 30055661, 30126689, 30471641, 30974989, 31115099, 31180841, 31320859, 31814929, 31952989, 32020229, 32154637, 32870587, 33004619, 33283423, 33638161, 33910967, 34051967, 34244467, 34451903, 34944479, 35083201, 35278493, 35493181, 35772127, 35974751, 36397657, 36535871, 36746159, 36793777, 37133527, 37201429, 37415429, 37771343, 37834949, 38188573, 38249929, 38459413, 39098303, 39235633, 39294443, 39418501, 39623069, 39825299, 40099183, 40312331, 40507391, 41285219, 41350039, 41694713, 41967469, 42323497, 42531397, 42720137, 42999403, 43426613, 43564949, 43747933, 43947811, 44011943, 44219039, 44628019, 44982811, 45559529, 45623209, 45696611, 45892267, 45955727, 46164121, 46303891, 46351619, 46488683, 46881217, 46944377, 47152291, 48357691, 48565409, 48770333, 49037929, 49674293, 50006819, 50461003, 50585723, 50653763, 50781221, 50973697, 51251293, 51375557, 51437653, 51638387, 52045451, 52372603, 52428499, 52549093, 52601903, 52737239, 52940183, 53354921, 53748193, 54015211, 54435497, 54628583, 54754121, 54956309, 55200709, 55332191, 55582379, 55675693, 56148923, 56279953, 56484443, 56541869, 56663077, 56854423, 56914931, 57119089, 57457063, 58142473, 58343029, 58480027, 58530161, 59354887, 59484941, 59551649, 59861143, 60274583, 60272263, 60590879, 60867101, 61055903, 61248067, 61422521, 62040401, 62221351, 62335921, 62394953, 62802671, 63111539, 63526081, 63797533, 64351327, 64798159, 64984669, 65075251, 65111099, 65242643, 65308403, 65637083, 66038839, 66228203, 66421273, 67011493, 67061569, 67604963, 67658729, 68409829, 68605993, 68851537, 69055457, 69158107, 69191387, 69317821, 69586633, 69770047, 70111903, 70168907, 70445411, 70916779, 71249831, 71419811, 71821553, 71886413, 72003587, 72068411, 72388213, 72793613, 72837223, 73384501, 73427867, 73596143, 73712489, 73764203, 74069659, 74297341, 74890051, 75710501, 75834727, 76018763, 76262477, 76789499, 76840241, 76964059, 77216053, 77760367, 77819893, 77925259, 78176713, 78368629, 78560473, 78692923, 79090177, 79107841, 79828261, 80024207, 80087951, 80227501, 80336021, 80512763, 80986247, 81167419, 81289721, 81329407, 81529403, 81656339, 81712339, 82111427, 82272263, 82461959, 82933547, 83040379, 83190659, 83524853, 83781787, 83936093, 84061949, 84929293, 85519883, 85828741, 86054327, 86179727, 86337179, 86384513, 86572349, 87301729, 87650939, 87713411, 88212899, 88478153, 88581937, 88971703, 89397131, 89724233, 89786453, 89894891, 90148921, 90346073, 90521737, 90608327, 90654257, 90762179, 90899621, 91082429, 91200751, 91257181, 91437251, 91757167, 91813489, 92144197, 92402137, 92503553, 92968433, 93276653, 93674143, 93724571, 93914869, 94026769, 94077089, 94568993, 94998989, 95121773, 95300203, 95517053, 95689501, 95806307, 96386041, 96625003, 96936517, 97125671, 97239143, 97465721, 97788143, 98171417, 98603623, 98695789, 98842717, 99025057, 99079879, 100007653, 100062343, 100359641, 100620251, 100717291, 101165507, 101268341, 101498161, 101891507, 101968549, 102293617, 102389513, 102564067, 103215691, 103522729, 103557901, 104082523, 104888243, 104989217, 105049181, 105351539, 105531131, 105644437, 105990473, 106163347, 106395841, 106521691, 106728137, 107442299, 107469361, 107575453, 107621957, 107985523, 108863701, 108909893, 109088009, 109272679, 109430749, 109555987, 109713853, 109726471, 110115077, 110226751, 110568203, 110613871, 110936239, 110927851, 111393041, 111370613, 111882473, 112059029, 112708823, 113137547, 113393057, 113510417, 113548307, 113658661, 113710351, 114403561, 114588751, 114876409, 115065689, 115378751, 115423003, 115504369, 115679293, 115624273, 115798909, 116075581, 116098139, 116453881, 116772829, 116816549, 117085091, 117512453, 117686249, 117802073, 117975749, 118228991, 118337069, 118517719, 119030929, 119333197, 119383519, 119491469, 119924281, 120074863, 120160367, 120331087, 120648079, 120862883, 121035059, 121192207, 121897771, 122054567, 122043989, 122352683, 122783203, 122905093, 123076489, 123643739, 123685519, 123963053, 124361969, 124475873, 124532813, 124809667, 125238731, 125352419, 125603033, 126043727, 126157127, 126327167, 126336803, 126450059, 126564877, 126589993, 126929113, 127049983, 127669961, 128338097, 128668159, 128668429, 128788987, 128893547, 129078223, 129070079, 129222403, 129904067, 129943927, 130103933, 130592599, 130768661, 131145187, 131184743, 131286871, 131662997, 132101143, 132140387, 132218803, 132369359, 132783869, 132870191, 132909163, 133275539, 133974091, 134259313, 134408441, 134413121, 134689421, 134744657, 134935897, 134923157, 135215629, 135312689, 135367709, 135608521, 135629293, 135895307, 136077103, 136313731, 137256767, 137478563, 137489893, 137719783, 137955691, 138119491, 138401077, 138944413, 139063919, 139355263, 139708021, 139691609, 140215693, 140378449, 140415697, 140587151, 140767483, 141290411, 141290711, 141587909, 142020077, 142109857, 142199677, 142244563, 142334287, 142762159, 142806757, 143174351, 143344429, 143809957, 143959987, 144056189, 144225799, 144762067, 145235477, 145288841, 145358401, 145406773, 145441421, 145610419, 145760717, 146045269, 146214071, 146579677, 146907611, 147441551, 147466229, 147634651, 147636469, 148178939, 148399897, 149138723, 149244299, 149220451, 149316329, 149493649, 149536747, 149872007, 149919491, 150345551, 151133351, 151395551, 151572283, 151896341, 152301889, 152429359, 152680841, 153023723, 153016727, 153111181, 153148969, 153367127, 153523247, 153723683, 153745829, 153849701, 154252897, 154338623, 154434107, 154497643, 154632839, 154684559, 154943039, 154974619, 155458189, 155777891, 156014501, 156518833, 156581177, 156725383, 157064497, 157013881, 157157711, 157291219, 157445083, 158151869, 158264089, 158663069, 158765213, 158979763, 159245221, 159428369, 159765239, 160265047, 160324919, 160354819, 160445969, 161149691, 161316889, 161415983, 161382079, 161860429, 162022559, 162131551, 162505867, 162747161, 163131623, 163189447, 164082833, 164255017, 164319317, 164491333, 164637743, 164723003, 164823059, 164753857, 165053521, 165224993, 165226847, 165178721, 165328109, 165897133, 166057163, 166084927, 166173281, 166641793, 166581313, 166691383, 166999421, 167026813, 167142007, 167163413, 167882527, 168019289, 168167093, 168232151, 168440161, 168674879, 169595303, 169953821, 170002817, 170161051, 170202469, 170228789, 170326613, 170352877, 170619893, 171007153, 171176321, 171194203, 171366359, 171598417, 171675793, 172184581, 172293151, 172226827, 172372267, 173133061, 173183501, 173307257, 173571721, 173728019, 173698253, 173925659, 174069971, 174393413, 174489509, 174598499, 174576287, 174731881, 174769159, 174854201, 174831641, 174964919, 175012679, 175453441, 175561123, 176049329, 176132659, 176287337, 176631463, 177450289, 177592381, 178053487, 178123963, 178633241, 178761607, 178866757, 178912589, 179053793, 179419391, 179572537, 179737793, 179850793, 179873321, 180144227, 180339613, 180465443, 180698963, 180635249, 180868349, 181066987, 181370927, 181628179, 182259967, 182256799, 182361997, 182535079, 182698979, 182791643, 182902127, 183330709, 183574123, 183712579, 183850963, 183809281, 183934931, 184190239, 184478813, 184423969, 184603061, 184728031, 184827613, 184939709, 185097433, 185260001, 185513953, 185625569, 185607619, 185744491, 185881291, 185966987, 186220183, 186389389, 187050151, 187212083, 187814227, 187730551, 188099113, 188124799, 188331379, 188453203, 189285067, 189491167, 190000487, 190090367, 190095977, 190189177, 190244809, 190223879, 190292341, 190368587, 190849679, 191001763, 191295719, 191669923, 192078763, 192225353, 192229799, 192469339, 192602323, 192756913, 192787783, 193035707, 192999479, 193145401, 193312349, 193634347, 193708961, 194385511, 194294227, 194713217, 194689291, 194922073, 194938721, 195157661, 195608587, 195682301, 195725969, 195813281, 195987809, 196405051, 196494553, 196638863, 196654891, 196984577, 197359693, 197560921, 197633867, 197763947, 198538313, 198553777, 198825589, 198799199, 198900883, 199001137, 199130557, 199273871, 199362347, 199505461, 199521499, 199821409, 199880063, 200009501, 200238433, 200295877, 200651681, 200964601, 201121469, 201789127, 201916927, 202186553, 202314149, 202114279, 202723699, 202735721, 203173693, 203442409, 203540321, 203878823, 203948713, 203976427, 204131663, 204067441, 204220903, 204332273, 204372647, 204411299, 205242223, 205505411, 205699357, 205551007, 205800631, 206067079, 206049967, 206484853, 206467537, 206928889, 207514117, 207930427, 208054267, 208354423, 208829177, 208937683, 208859459, 209333569, 209340823, 209388929, 209399929, 209619547, 209798129, 210047531, 210200143, 210202151, 210410429, 210401441, 210508471, 210488767, 210525709, 210551167, 210733871, 210814871, 210936311, 211042501, 211052573, 211355797, 211421351, 211795211, 212203781, 212269039, 212389783, 212914447, 212933423, 213140069, 213260441, 213340649, 213547163, 213627299, 213768617, 213903931, 213968357, 214340549, 214548769, 214504321, 214513073, 215217859, 215219281, 215835187, 215781809, 215931649, 216027391, 216279473, 216649313, 216735817, 216830179, 216743411, 216680021, 217127381, 217276453, 217431983, 217588223, 217657721, 217719847, 218017223, 217928959, 218241941, 218984221, 219182303, 219188971, 219160729, 219697831, 219838847, 219873697, 220130389, 220425437, 220540577, 220498051, 220558529, 220679341, 220935529, 220871687, 220921231, 221525077, 221807819, 221676881, 221654717, 221724511, 222033437, 222488527, 222660929, 222600017, 222837863, 222842611, 222901457, 223047337, 223456309, 223519339, 223511641, 223840157, 223798963, 223803191, 223861357, 224056249, 224168101, 224474879, 225088291, 225190501, 225301849, 225366431, 225551591, 225588599, 226311139, 226401817, 226428227, 226465091, 226686107, 226709033, 227034013, 227093407, 227937313, 228156913, 228217943, 228327479, 228441583, 228307243, 228362933, 228880427, 229096279, 229258577, 229651661, 229687889, 229868909, 230225477, 230280511, 230282123, 230567803, 230710607, 231033547, 231002843, 231163957, 231201073, 231362003, 231207721, 231315109, 231371111, 231425993, 231550483, 231712009, 231644081, 231645241, 231769259, 231858217, 231982519, 232283561, 232301567, 232724911, 232777817, 233024437, 233024357, 233200217, 233287963, 233287727, 233498563, 233673431, 233602091, 233618849, 234074693, 234072653, 234826591, 234913061, 234911101, 235085713, 235115917, 235395269, 235534909, 235497721, 236214751, 236159237, 236226589, 236169299, 236167639, 236460481, 236720503, 236718611, 236821379, 236992499, 237129251, 237647831, 237761257, 237863317, 238315097, 238435231, 238466563, 238685533, 238567321, 238561601, 238764017, 238898801, 239018179, 239201597, 239268797, 239406373, 239570801, 239615963, 239761289, 239739263, 240117323, 240580441, 240665611, 240606077, 240809509, 241182833, 241259591, 241213979, 241520179, 241455509, 241488521, 241587509, 241949849, 241935977, 242278409, 242376821, 242324713, 242507119, 242624021, 242562487, 242763371, 242739389, 242691329, 242610617, 243081473, 243000377, 243046291, 243143491, 243202703, 243377713, 243493583, 243795463, 243937541, 244130597, 244227017, 244412747, 244400539, 245264221, 245583979, 245871701, 245871259, 245781043, 245895773, 245812013, 245616853, 245750381, 245998043, 246347389, 246359587, 246555983, 246681983, 247086137, 247020331, 247305797, 247282949, 247209139, 247302883, 247661819, 247634381, 247879883, 247992793, 247917911, 248104127, 248286977, 248399551, 248683529, 248391413, 248464267, 248708197, 248820251, 248811583, 249035459, 249239377, 249043643, 249336883, 249369097, 249751987, 249843427, 249794443, 249986327, 249988523, 250381007, 250491841, 251285777, 251195873, 251798219, 251707847, 252098477, 252047479, 252057277, 252287449, 252406183, 252213977, 252262921, 252342631, 252481781, 252990611, 252998467, 252946963, 252993373, 253152121, 253231471, 253279283, 253295353, 253272737, 253387787, 253753561, 254010881, 254446363, 254340787, 254366677, 254412941, 254549731, 254525651, 254431391, 254786507, 254939449, 254824099, 254823917, 254897737, 255082721, 255049439, 255086149, 255172153, 255393263, 255398839, 255857593, 255929789, 256431211, 256250959, 256140583, 256589791, 256541581, 256527893, 256521371, 256780793, 256921013, 257026019, 256990973, 257242597, 257360347, 257367109, 257861339, 258035573, 258509257, 258640979, 258568991, 258588053, 258670649, 258990617, 258960529, 258921343, 259128179, 259146269, 258908303, 258685417, 259127689, 259139149, 259468361, 259452553, 259528769, 259609613, 259534673, 259658281, 259889257, 260130421, 260220997, 260370937, 260482679, 261167903, 261269233, 261488629, 261589859, 261669323, 261652351, 261709961, 262029991, 262109119, 262048351, 262206247, 262285087, 262805173, 262787597, 262984031, 263044699, 263362973, 263419147, 263479247, 263579161, 263752913, 264173839, 264343663, 264450269, 264431749, 264648721, 264585829, 264806119, 264835169, 264889747, 265300649, 265351673, 265265983, 265285123, 265691819, 265885493, 265843859, 266015023, 265928573, 265889653, 266186281, 266499371, 267049879, 267054979, 267177497, 267274951, 267347401, 267384287, 267188231, 267355169, 267526423, 267742681, 267862073, 267888823, 267738257, 268212779, 268237331, 268569887, 268741247, 268908979, 269005001, 269219723, 269365763, 269535779, 269631409, 269702767, 270128119, 270130579, 270298337, 270416593, 270394721, 270282973, 270285991, 270385487, 270411893, 270789403, 270651481, 271145443, 271124213, 270940003, 271010293, 271338269, 271222519, 271432789, 271922839, 272319317, 272295791, 272318633, 272504807, 272527991, 272760043, 272689411, 272757481, 272754661, 273332393, 273308137, 273377383, 273469433, 273653389, 273603611, 273671771, 273762539, 273712261, 273662861, 273543461, 273469061, 273881081, 273902227, 274244977, 274380511, 274471277, 274585813, 274860919, 274810007, 274924387, 274943231, 274965407, 275170013, 275260303, 275418659, 275368913, 275479133, 275377351, 275716741, 275784571, 276164891, 276184417, 276037603, 276006443, 276437971, 276194021, 276670487, 276640961, 276753913, 276726977, 276382321, 276446509, 276945401, 276839263, 276972931, 276991097, 276939347, 277493947, 277508423, 277665929, 277883029, 278082319, 278078797, 278207959, 278130847, 278333311, 278395879, 278430083, 278397989, 278358139, 278531543, 278980397, 279091573, 279211003, 279276793, 279790649, 279386021, 279406409, 279627697, 279630149, 279736087, 279801433, 279857551, 279879263, 279844937, 279935833, 280045817, 280255837, 280190987, 280295689, 280310531, 280345201, 280179727, 280208867, 280268147, 280366787, 280484891, 280504547, 280412903, 280471679, 280376683, 280504831, 280487653, 280520687, 280737679, 280935247, 280929349, 281037749, 281286983, 281224327, 281130163, 280808029, 280890551, 280928741, 281175551, 281327429, 281409559, 281554811, 281553893, 281901331, 281913389, 282070027, 282177167, 282370633, 282565981, 282589121, 282733057, 282921007, 282913849, 282892279, 283002799, 283241561, 283957559, 283994111, 283945687, 283992721, 284003267, 284057747, 283920863, 283802003, 283964363, 284149961, 284177911, 284119937, 284017889, 283993499, 283951193, 284240863, 284232577, 284215957, 284129569, 284627687, 284480377, 284559131, 284507347, 284760337, 285257191, 285204527, 285213001, 285212513, 285394871, 285367853, 285776339, 285731777, 285721367, 285650263, 285586793, 285585121, 285556963, 285485363, 286108399, 285755123, 285918377, 286151251, 286191649, 286381141, 286421263, 286912817, 286909369, 287061821, 287068219, 287316793, 287376367, 287132273, 287095297, 287671207, 287918977, 288075691, 288065101, 288242623, 288344747, 288377027, 288726121, 288752617, 288423881, 288363997, 288330883, 288421277, 288581339, 288757109, 288948479, 289108217, 289380449, 289315891, 289533347, 289502371, 289746529, 289847249, 290133869, 289853177, 289941679, 289960277, 290000303, 290151863, 290282059, 290187691, 290068591, 290125981, 290113591, 290088763, 290205821, 290165893, 290295197, 290227727, 290272247, 290682389, 290561597, 290411213, 290413063, 290627509, 290492863, 290620739, 290761613, 290837699, 290769113, 290923979, 291274603, 291513349, 291569647, 291472879, 291306989, 291656881, 291448589, 291476813, 291435611, 291491819, 291561899, 291492293, 291868589, 291896333, 292495309, 292397113, 292493911, 292451603, 292602853, 292574017, 292387259, 292483999, 292522019, 292504613, 292517993, 292432033, 292762571, 293453107, 293549303, 293575679, 293530229, 293650387, 293704909, 293977279, 293985451, 294104501, 294303109, 294113609, 294126389, 294574187, 294593023, 294627497, 294912353, 294523849, 294434177, 294693209, 294730421, 295038677, 295235627, 295104001, 295321307, 295098581, 295122869, 295257863, 294849389, 294984071, 294962347, 294877717, 294860743, 294989939, 295270247, 295416221, 295411607, 295592321, 295848281, 295871561, 295906421, 295941209, 295865483, 295900139, 295923203, 295585211, 296007617, 295785517, 296236081, 296182123, 295988557, 296040223, 295985941, 296005253, 295822231, 295976413, 296200159, 296346539, 296452237, 296503399, 296565389, 296520299, 296552651, 296544697, 296606411, 296638571, 296670659, 296654263, 296468741, 296511077, 296413933, 296635459, 296689577, 296760883, 296851367, 296783141, 296815471, 296916043, 297206197, 297067751, 297178267, 297189181, 297239251, 297180253, 297519851, 297490183, 297569941, 297639611, 297390341, 297479773, 297389123, 297577363, 298053089, 297982331, 298230071, 298335407, 298403593, 298460473, 298419061, 298296491, 298243433, 298380659, 298408571, 298654871, 298670809, 298607599, 298495663, 298571641, 298656539, 298862581, 298986469, 299013433, 298827539, 298390153, 298494881, 298521101, 298464503, 298725443, 298712173, 298646371, 298593863, 298558411, 298723267, 298609459, 298437593, 298501807, 298435057, 298460077, 298562933, 298509901, 298829681, 298932217, 298878977, 298958731, 298944257, 298937839, 299031739, 299195227, 299366699, 299607767, 299779063, 299640529, 299610341, 299742407, 299765927, 299851267, 300145889, 299603501, 299657009, 299810843, 299956841, 299963239, 299868607, 299967923, 300074479, 299957167, 300116437, 300138217, 300181561, 300279977, 300479251, 300455101, 300156401, 300163469, 300111743, 300132719, 299958611, 300080381, 299874643, 300181249, 300163211, 300169907, 300151801, 300126991, 300034199, 300042157, 300061777, 299892049, 300095083, 300044791, 299811263, 299830319, 299722831, 299684699, 299355337, 300004703, 300281701, 300325591, 300248413, 299809541, 299876959, 299671973, 299212139, 299229443, 299240939, 299408419, 299598307, 299568047, 299477777, 299719313, 299714731, 299635033, 300025529, 300281957, 300196151, 300040777, 299986957, 299863609, 299552501, 299491679, 299179963, 299194939, 299242049, 298907383, 299010707, 299200921, 298979743, 299725343, 299734679, 299545067, 299457149, 299706377, 299492803, 299538653, 299478181, 299680307, 299689067, 299849611, 299862571, 300150313, 300285919, 300478201, 300294481, 300347479, 300502487, 300310139, 300223829, 300247349, 300534643, 300611687, 300619247, 300630527, 300543137, 300766289, 300543319, 300382421, 300754681, 300794731, 300607471, 300650897, 301025737, 301108793, 301337417, 301248047, 301261151, 301204627, 301114837, 301327847, 301300801, 301352327, 301536661, 301506391, 301696529, 301699469, 301441729, 301380829, 301397821, 301456151, 301458887, 301400251, 301439041, 301841347, 302024381, 301663711, 301477651, 301516081, 301847047, 302211347, 302326133, 302232011, 302234267, 302146577, 302480159, 302522317, 302560243, 302498879, 302680009, 302614409, 302733611, 302671687, 302438453, 302342387, 302246177, 302569031, 302684633, 302380667, 302215717, 302288477, 302506613, 302309981, 302212223, 302213663, 302114321, 302119889, 301953511, 301957471, 301972591, 302221333, 302122231, 302092513, 302234869, 301827121, 302005351, 302152831, 302122033, 302369251, 302199809, 302200589, 302308319, 302309783, 302035159, 302214509, 302010041, 302152813, 302540627, 302471863, 302542211, 302753111, 302719117, 302720017, 302755511, 302583109, 302653493, 302584729, 302689963, 302759711, 302551187, 302446877};
int main() {
    for(int i = 0; i < 2000; i++)
        printf("%dn", a[i]);
    return 0;
}

I 处女座的测验（二）

做了，但是TLE，没有AC，还是简单说一下思路吧（如果以AC为目的可以直接去看std）
链接：https://ac.nowcoder.com/acm/contest/327/I?&headNav=acm
来源：牛客网

时间限制：C/C++ 2秒，其他语言4秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述
现在处女座顺利的完成了测验，处女座想要知道知道自己输出的结果是否正确。他希望知道自己有自己输出的数中有多少对是不满足要求的。
更具体的，处女座想知道下面程序段的答案

int main()
{
         int n;
         cin>>n;
         for (int i=1;i<=n;i++)
                   cin>>a[i];
         int ans=0;
         for (int i=1;i<=n;i++)
         {
                   for (int j=i+1;j<=n;j++)
                   {
						if(τ(a[i]∗a[j])≤10)ans=ans+1;
                   }
         }
         cout<<ans<<endl;
         return 0;
}

其中为n的因子的个数

输入描述:
两行
第一行一个整数n
第二行n个整数，a1,a2,…,an

2<=n<=2000, 1<=ai<=3*108

输出描述:
一行，一个整数ans

示例1

输入
7
34 45 23 12 63 23 90

输出
3

备注:
不保证任意两个整数互质

没有AC，也就是说我这里是用最朴素的办法来求出一个数的因数个数
如果题目没有说不保证互质，那这题就简单一小半。一个显而易见的结论是：如果A和B互质，且A有p个因子，B有q个因子，则他们的乘积AB有pq个因子
但是这里说不保证互质，所以这个结论就不能用了。只能先算出来乘积AB再找它的因子。
找一个数X的因子个数有一个结论，将X进行唯一分解，即分解为若干个质数的乘积，即：
$X = p_1^{k_1}p_2^{k_2}p_3^{k_3}...p_s^{k_s}$
则X的因子个数为 $k_1+1)(k_2+2)(k_3+3)...(k_4+4)$
进行质因数分解的部分可以在 $O (n)$ 的复杂度内解决，可惜这还是不够，还是TLE了

J 处女座的期末复习

链接：https://ac.nowcoder.com/acm/contest/327/J?&headNav=acm
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述
快要期末考试了，处女座现在有n门课程需要考试，每一门课程需要花ai小时进行复习，考试的起始时间为bi，处女座为了考试可以不吃饭不睡觉，处女座想知道他能否复习完所有的科目（即在每一门考试之前复习完该科目）。每一门课的考试时间都为两小时。

输入描述:
第一行一个整数n
第二行n个整数a1,a2,…,an,表示每门课需要复习的时间
第三行n个整数b1,b2,…,bn,表示每门课考试的时间

1<=n<=105
0<=ai<=109
0<=bi<=109

输出描述:
如果处女座能复习完，输出”YES”，否则输出”NO”

示例1

输入
3
0 1 1
2 6 4

输出
YES

说明
在0-1小时复习第2门课，
在1-2小时复习第3门课，
在2-4小时考第1门课，
在4-6小时考第3门课，
在6-8小时考第2门课

备注:
考试时不能复习，保证考试时间不会重叠。
复习可以拆开，只要复习时间够了即可。

最开始的题目中没有说考试时间不会重叠的问题，最主要的是没有说复习时间可以拆开的问题，导致我第一眼看到这个问题就在往区间覆盖问题的变形上面去想，然后打死想不通，后来给了提示马上就想出来了。
显然是个贪心的问题。作为学生这个应该我们本身也有体会。如果要安排好每一科的复习的话，必然是最先考的最先复习，因为考完之后就不能再复习这一科了。
所以贪心策略是：把考试按照时间顺序排序，最先复习第一科，再复习第二科，直到某一刻的复习时间不够或者所有的科目都复习完毕为止
注意算时间的时候要考虑每场考试持续的2个小时
这题没什么细节，只要读懂题意想到贪心就能直接做

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
struct Node {
    int a, b;
    bool operator < (const Node& node) const {
        return b < node.b;
    }
} P[maxn];
int main() {
    int n; scanf("%d", &n);
    P[0].a = P[0].b = -2;
    for(int i = 1; i <= n; i++) scanf("%d", &P[i].a);
    for(int i = 1; i <= n; i++) scanf("%d", &P[i].b);
    sort(P, P+n+1);
    int time = 0;
    for(int i = 1; i <= n; i++) {
        time += P[i].b - P[i-1].b - 2;
        if(time < P[i].a) {
            printf("NOn");
            return 0;
        }
        time -= P[i].a;
    }
    printf("YESn");
    return 0;
}

最后

以上就是贤惠猫咪为你收集整理的牛客寒假算法基础集训营2 非官方题解的全部内容，希望文章能够帮你解决牛客寒假算法基础集训营2 非官方题解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：ACM
浏览次数：72 次浏览
发布日期：2023-08-01 18:20:04
本文链接：https://www.kaopuke.com/article/k-p-k_14_uzo_22_f3_14__7__6_5.html

牛客寒假算法基础集训营2 非官方题解

概述

A 处女座的签到题

B 处女座与cf

C 处女座的砝码

D 处女座与重修费

E 处女座与汉明距离

F 处女座与宝藏

G 处女座与复读机

H 处女座的测验（一）

I 处女座的测验（二）

J 处女座的期末复习

最后

评论列表共有 0 条评论

发表评论取消回复

牛客寒假算法基础集训营2 非官方题解

概述

A 处女座的签到题

B 处女座与cf

C 处女座的砝码

D 处女座与重修费

E 处女座与汉明距离

F 处女座与宝藏

G 处女座与复读机

H 处女座的测验（一）

I 处女座的测验（二）

J 处女座的期末复习

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

发表评论取消回复