我是靠谱客的博主 外向背包,这篇文章主要介绍sklearn学习记录(5)-svm官方案例解读非线性最大间隔法自定义核带权样本为不平衡的类分离超平面三种SVM内核具有单变量特征选择的,现在分享给大家,希望可以做个参考。
文章目录
- 非线性
- 最大间隔法
- 自定义核
- 带权样本
- 为不平衡的类分离超平面
- 三种SVM内核
- 具有单变量特征选择的
非线性
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
xx, yy = np.meshgrid(np.linspace(-3, 3, 500), np.linspace(-3, 3, 500)) # 格点矩阵, 500*500
np.random.seed(0) # 随机数种子,确保不同人执行案例的结果一样
X = np.random.randn(300, 2) # 300行*2列的矩阵,具有标准正态分布
Y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0) # 每行第一列大于0的结果 与 和每行第二列数大于0的结果异或 <==> 每行两个数是否异号
# fit the model
clf = svm.NuSVC(gamma='auto') # 分类器
clf.fit(X, Y) # 拟合模型
# plot the decision function for each datapoint on the grid
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]) # np.c_是按行连接两个矩阵,就是把两矩阵左右相加;这样就将xx和yy数据合并在了一起
Z = Z.reshape(xx.shape) # 重排成和x一样500*500的矩阵
plt.imshow(Z, interpolation='nearest', extent=(xx.min(), xx.max(), yy.min(), yy.max()), aspect='auto', origin='lower', cmap=plt.cm.PuOr_r) # 根据函数距离,绘制颜色
contours = plt.contour(xx, yy, Z, levels=[0], linewidths=2, linestyles='dashed') # 以levels=[0]为边界,绘制轮廓,线宽2,线型虚线
plt.scatter(X[:, 0], X[:, 1], s=30, c=Y, cmap=plt.cm.Paired, edgecolors='k') # 绘制训练集的散点图
plt.xticks(()) # 去掉横坐标刻度
plt.yticks(()) # 去掉纵坐标刻度
plt.axis([-3, 3, -3, 3]) # 设置刻度范围
plt.show() # 显示图像
其中值得注意的是函数距离的计算方法,这里引用李航老师的《统计学习方法》
最大间隔法
《统计学习方法》中也给出了这种方法的步骤

调用代码如下
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
# we create 40 separable points
X, y = make_blobs(n_samples=40, centers=2, random_state=6) # 生成2个中心的40个样本,random_state指定随机数种子
# fit the model, don't regularize for illustration purposes
clf = svm.SVC(kernel='linear', C=1000) # C越大训练集测试时准确率越高,但泛化能力弱
clf.fit(X, y) # 拟合模型
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired) # 绘散点图
# plot the decision function
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
# 下面创建数据来评价自己生成的模型
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx) # 生成格点矩阵
xy = np.vstack([XX.ravel(), YY.ravel()]).T # np.vstack垂直拼接矩阵,之后转置
Z = clf.decision_function(xy).reshape(XX.shape) # 计算函数距离并重排成XX的同型矩阵
ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, inestyles=['--', '-', '--']) # 以-1、0、1为界分割,绘制决策边界
ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100, linewidth=1, facecolors='none', edgecolors='k') # 绘制支持向量
plt.show() # 显示
其中值得注意的是支持向量的定义

自定义核
简单使用支持向量机对样本进行分类,除了内核变化,其他与上面的例子差不多。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
# import some data to play with
iris = datasets.load_iris()
X = iris.data[:, :2] # we only take the first two features. We could
# avoid this ugly slicing by using a two-dim dataset
Y = iris.target
def my_kernel(X, Y):
"""
We create a custom kernel:
(2 0)
k(X, Y) = X ( ) Y.T
(0 1)
"""
M = np.array([[2, 0], [0, 1.0]])
return np.dot(np.dot(X, M), Y.T)
h = .02 # step size in the mesh
# we create an instance of SVM and fit out data.
clf = svm.SVC(kernel=my_kernel) # 传入自定义的内核
clf.fit(X, Y) # 拟合模型
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=Y, cmap=plt.cm.Paired, edgecolors='k')
plt.title('3-Class classification using Support Vector Machine with custom'
' kernel')
plt.axis('tight')
plt.show()
带权样本
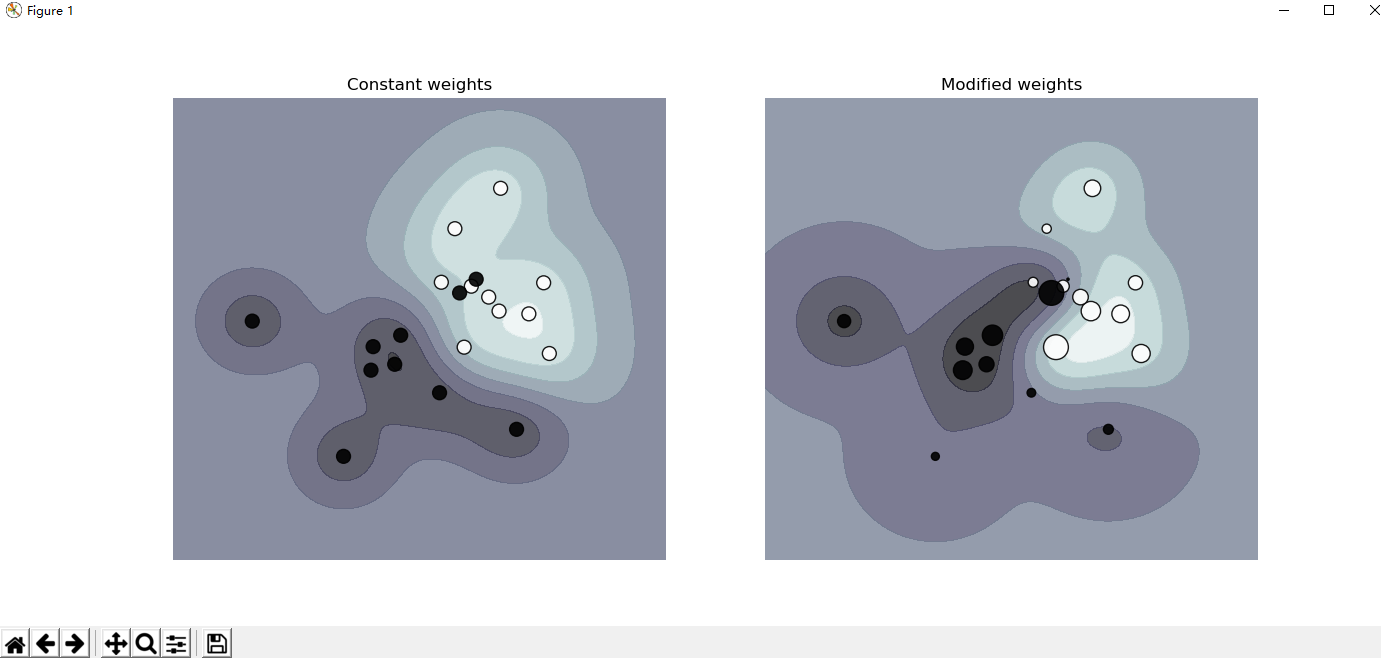
绘制加权数据集的决策函数,其中点的大小与其权重成正比。
样本加权会重新缩放C参数,这意味着分类器将更多的重点放在正确设置这些点上。效果通常可能很微妙。为了强调此处的效果,我们特别权重离群值,使决策边界的变形非常明显。
"""
=====================
SVM: Weighted samples
=====================
Plot decision function of a weighted dataset, where the size of points
is proportional to its weight.
The sample weighting rescales the C parameter, which means that the classifier
puts more emphasis on getting these points right. The effect might often be
subtle.
To emphasize the effect here, we particularly weight outliers, making the
deformation of the decision boundary very visible.
"""
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
def plot_decision_function(classifier, sample_weight, axis, title):
# plot the decision function
xx, yy = np.meshgrid(np.linspace(-4, 5, 500), np.linspace(-4, 5, 500)) # 网格矩阵
Z = classifier.decision_function(np.c_[xx.ravel(), yy.ravel()]) #
Z = Z.reshape(xx.shape)
# plot the line, the points, and the nearest vectors to the plane
axis.contourf(xx, yy, Z, alpha=0.75, cmap=plt.cm.bone) # 根据预测结果,绘制背景
axis.scatter(X[:, 0], X[:, 1], c=y, s=100 * sample_weight, alpha=0.9,
cmap=plt.cm.bone, edgecolors='black') # 绘制20个散点
axis.axis('off') # 取消坐标轴
axis.set_title(title) # 设置标题
# we create 20 points 创建数据集,20个点
np.random.seed(0) # 随机数种子确保不同人运行的案例一样
X = np.r_[np.random.randn(10, 2) + [1, 1], np.random.randn(10, 2)] # 20个点的横纵坐标
y = [1] * 10 + [-1] * 10 # 20个点的标签
sample_weight_last_ten = abs(np.random.randn(len(X))) # 随机生成不同的20个权重值,对应20个点
sample_weight_constant = np.ones(len(X)) # 权重向量都是1,相当于无权重差异
# and bigger weights to some outliers
sample_weight_last_ten[15:] *= 5
sample_weight_last_ten[9] *= 15
# for reference, first fit without sample weights
# fit the model
clf_weights = svm.SVC(gamma=1) # 构建有权重SVC
clf_weights.fit(X, y, sample_weight=sample_weight_last_ten) # 拟合
clf_no_weights = svm.SVC(gamma=1) # 构建无权重SVC
clf_no_weights.fit(X, y) # 拟合
fig, axes = plt.subplots(1, 2, figsize=(14, 6)) # 子图一行两列,大小(14, 6)
plot_decision_function(clf_no_weights, sample_weight_constant, axes[0],
"Constant weights") # 将决策边界的绘制封装成了函数,方便复用,先绘制了无权重的
plot_decision_function(clf_weights, sample_weight_last_ten, axes[1],
"Modified weights")
plt.show()
为不平衡的类分离超平面
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs
# we create two clusters of random points
n_samples_1 = 1000 # 第一个簇的样本数
n_samples_2 = 100 # 第二个簇的样本数
centers = [[0.0, 0.0], [2.0, 2.0]] # 两个簇的中心
clusters_std = [1.5, 0.5] # 标准差
X, y = make_blobs(n_samples=[n_samples_1, n_samples_2],
centers=centers,
cluster_std=clusters_std,
random_state=0, shuffle=False) # 按需求创建训练数据集
# fit the model and get the separating hyperplane
clf = svm.SVC(kernel='linear', C=1.0) # 构建线性核的SVC
clf.fit(X, y) # 拟合
# fit the model and get the separating hyperplane using weighted classes
wclf = svm.SVC(kernel='linear', class_weight={1: 10}) # 用权重构建SVC
wclf.fit(X, y) # 拟合
# plot the samples
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors='k') # 绘制训练集的散点图
# plot the decision functions for both classifiers
ax = plt.gca() # 获得坐标轴对象
xlim = ax.get_xlim() # 得到x取值范围
ylim = ax.get_ylim() # 得到y取值范围
# create grid to evaluate model
# 构建数据集用于预测
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
# get the separating hyperplane
Z = clf.decision_function(xy).reshape(XX.shape) # 预测
# plot decision boundary and margins
a = ax.contour(XX, YY, Z, colors='k', levels=[0], alpha=0.5, linestyles=['-']) # 绘制背景
# get the separating hyperplane for weighted classes
Z = wclf.decision_function(xy).reshape(XX.shape) # 预测
# plot decision boundary and margins for weighted classes
b = ax.contour(XX, YY, Z, colors='r', levels=[0], alpha=0.5, linestyles=['-']) # 绘制背景
plt.legend([a.collections[0], b.collections[0]], ["non weighted", "weighted"],
loc="upper right") # 图例
plt.show() # 展示图片
三种SVM内核
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
# Our dataset and targets 构建训练集的16个点
X = np.c_[(.4, -.7),
(-1.5, -1),
(-1.4, -.9),
(-1.3, -1.2),
(-1.1, -.2),
(-1.2, -.4),
(-.5, 1.2),
(-1.5, 2.1),
(1, 1),
# --
(1.3, .8),
(1.2, .5),
(.2, -2),
(.5, -2.4),
(.2, -2.3),
(0, -2.7),
(1.3, 2.1)].T # 16个点的横纵坐标
Y = [0] * 8 + [1] * 8 # 16个点的标签,前8个位0,后8个为1
# figure number
fignum = 1 # 由于要绘制多个图,这个变量用于记录当前图片的个数
# fit the model
for kernel in ('linear', 'poly', 'rbf'): # 循环绘制三种核的结果
clf = svm.SVC(kernel=kernel, gamma=2) # 创建相应核的SVC
clf.fit(X, Y) # 拟合
# plot the line, the points, and the nearest vectors to the plane
plt.figure(fignum, figsize=(4, 3)) # 设置相应的画布对象
plt.clf() # 清空画布
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80,
facecolors='none', zorder=10, edgecolors='k') # 绘制决策向量
plt.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired,
edgecolors='k') # 绘制训练集散点图
plt.axis('tight') #tight:坐标轴数据显示更明细
# 声明坐标轴的边界
x_min = -3
x_max = 3
y_min = -3
y_max = 3
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j] # 构造网格
Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]) # 预测扁平化后的数据
# Put the result into a color plot
Z = Z.reshape(XX.shape) # 将扁平的数据矩阵形状还原
plt.figure(fignum, figsize=(4, 3))
plt.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired) # 根据Z的正负,绘制不同的背景颜色
plt.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'],
levels=[-.5, 0, .5]) # 绘制边界,0的边界为实线, 正负0.5为虚线
# 设置横纵坐标界限
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
# 取消横纵坐标标签
plt.xticks(())
plt.yticks(())
fignum = fignum + 1 # 完成一张绘图,计数+1
plt.show()
具有单变量特征选择的
本示例说明如何在运行SVC(支持向量分类器)之前执行单变量特征选择以改善分类分数。我们使用虹膜数据集(4个特征)并添加36个非信息特征。我们发现,当我们选择大约10%的功能时,我们的模型将获得最佳性能。
# #############################################################################
# Import some data to play with
X, y = load_iris(return_X_y=True) # 加载虹膜数据
# Add non-informative features
np.random.seed(0) # 设置随机数种子
X = np.hstack((X, 2 * np.random.random((X.shape[0], 36)))) # 加入噪声
# #############################################################################
# Create a feature-selection transform, a scaler and an instance of SVM that we
# combine together to have an full-blown estimator
clf = Pipeline([('anova', SelectPercentile(chi2)),
('scaler', StandardScaler()),
('svc', SVC(gamma="auto"))]) # 组装非类器
# #############################################################################
# Plot the cross-validation score as a function of percentile of features
score_means = list()
score_stds = list()
percentiles = (1, 3, 6, 10, 15, 20, 30, 40, 60, 80, 100) # 预先设定的一些百分数
for percentile in percentiles: # 以不同的百分数执行
clf.set_params(anova__percentile=percentile) # 设置分类器的参数
this_scores = cross_val_score(clf, X, y) # 获得分类器的得分
score_means.append(this_scores.mean()) # 用列表记录当前参数分类器得分均值
score_stds.append(this_scores.std()) # 用列表记录当前参数得分器的标准差
plt.errorbar(percentiles, score_means, np.array(score_stds)) # 绘制图像
plt.title('Performance of the SVM-Anova varying the percentile of features selected') # 标题
plt.xticks(np.linspace(0, 100, 11, endpoint=True)) # 0到100等间隔11个点,包含100这个终点
plt.xlabel('Percentile') # x轴# 百分数
plt.ylabel('Accuracy Score') # 准确率得分
plt.axis('tight') #tight:坐标轴数据显示更明细
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC
X, y = make_blobs(n_samples=40, centers=2, random_state=0) # 准备训练数据:40个样本点,2个中心
plt.figure(figsize=(10, 5)) # 准备画板
for i, C in enumerate([1, 100]):# (i,C)--(0,1)->(1,100)
# "hinge" is the standard SVM loss
clf = LinearSVC(C=C, loss="hinge", random_state=42).fit(X, y) # 用线性svc进行分类
# obtain the support vectors through the decision function
decision_function = clf.decision_function(X) # 获得决策边界
# we can also calculate the decision function manually
# decision_function = np.dot(X, clf.coef_[0]) + clf.intercept_[0]
support_vector_indices = np.where((2 * y - 1) * decision_function <= 1)[0]# 支持向量的索引
support_vectors = X[support_vector_indices] # 取出相应的支持向量
plt.subplot(1, 2, i + 1) # 子图
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired) # 绘制样本散点图
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50),
np.linspace(ylim[0], ylim[1], 50)) # 格点矩阵
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])# 获得格点矩阵对应的决策边界
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])# 绘制边界
plt.scatter(support_vectors[:, 0], support_vectors[:, 1], s=100,
linewidth=1, facecolors='none', edgecolors='k') # 绘制散点图,标出支持向量
plt.title("C=" + str(C)) # 标题
plt.tight_layout() # 固定布局
plt.show()
最后
以上就是外向背包最近收集整理的关于sklearn学习记录(5)-svm官方案例解读非线性最大间隔法自定义核带权样本为不平衡的类分离超平面三种SVM内核具有单变量特征选择的的全部内容,更多相关sklearn学习记录(5)-svm官方案例解读非线性最大间隔法自定义核带权样本为不平衡内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复