Numpy基础
本文基于Datawhale提供的Pandas学习资料。
均为本人理解,如有不足或错误地方欢迎补充批评指正,如有侵权,联系速删。
1. Numpy数组的构造
最一般的方法是通过 array 来构造:
np.array([1,2,3])
# array([1, 2, 3])
等差序列: np.linspace, np.arange
np.linspace(1,5,11) # 起始、终止(包含)、样本个数
# array([1. , 1.4, 1.8, 2.2, 2.6, 3. , 3.4, 3.8, 4.2, 4.6, 5. ])
np.arange(1,5,2) # 起始、终止(不包含)、步长
#array([1, 3])
特殊矩阵: zeros, eye, full
np.zeros((2,3)) # 传入元组表示各维度大小
#array([[0., 0., 0.],
# [0., 0., 0.]])
np.eye(3) # 3*3的单位矩阵
#array([[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]])
np.eye(3, k=1) # 偏移主对角线1个单位的伪单位矩阵
#array([[0., 1., 0.],
# [0., 0., 1.],
@ [0., 0., 0.]])
np.full((2,3), 10) # 元组传入大小,10表示填充数值
#array([[10, 10, 10],
# [10, 10, 10]])
np.full((2,3), [1,2,3]) # 每行填入相同的列表
#array([[1, 2, 3],
# [1, 2, 3]])
随机矩阵: np.random
最常用的随机生成函数为 rand, randn, randint, choice ,它们分别表示0-1均匀分布的随机数组、标准正态的随机数组、随机整数组和随机列表抽样:
np.random.rand(3) # 生成服从0-1均匀分布的三个随机数
# array([0.10362482, 0.88047962, 0.06563272])
np.random.rand(3, 3) # 注意这里传入的不是元组,每个维度大小分开输入
#array([[0.2154583 , 0.40050334, 0.52756904],
# [0.10163278, 0.26863291, 0.67904088],
# [0.99421931, 0.01298826, 0.92643964]])
对于服从区间 a 到 b 上的均匀分布可以如下生成:
a, b = 5, 15
(b - a) * np.random.rand(3) + a
#array([9.7045308 , 7.44001917, 6.96897267])
可以选择已有的库函数:
np.random.uniform(5, 15, 3)
#array([11.86854175, 12.20529958, 9.69123879])
randn 生成了 N(0,I) 的标准正态分布:
np.random.randn(3)
#array([-1.43562244, 0.50142216, 2.12752728])
np.random.randn(2, 2)
#array([[-0.21882606, -0.50199747],
# [ 1.33332274, -0.02438479]])
对于服从方插为 σ²均值为 μ 的一元正态分布可以如下生成:
sigma, mu = 2.5, 3
mu + np.random.randn(3) * sigma
#array([7.59554985, 2.94427692, 3.45210924])
np.random.normal(3, 2.5, 3)
# array([4.34152104, 4.97592798, 2.47244767])
randint 可以指定生成随机整数的最小值最大值(不包含)和维度大小:
ow, high, size = 5, 15, (2,2) # 生成5到14的随机整数
np.random.randint(low, high, size)#不包括high
#array([[12, 8],
# [ 8, 11]])
choice 可以从给定的列表中,以一定概率和方式抽取结果,当不指定概率时为均匀采样,默认抽取方式为有放回抽样(从给定的列表中随机抽样组成列表):
my_list = ['a', 'b', 'c', 'd']
np.random.choice(my_list, 2, replace=False, p=[0.1, 0.7, 0.1 ,0.1])
#array(['b', 'a'], dtype='<U1')
np.random.choice(my_list, (3,3))
#
#array([['d', 'd', 'a'],
# ['d', 'b', 'c'],
# ['a', 'b', 'c']], dtype='<U1')
当返回的元素个数与原列表相同时,不放回抽样等价于使用 permutation 函数,即打散原列表:
np.random.permutation(my_list)
# array(['c', 'a', 'd', 'b'], dtype='<U1')
最后,需要提到的是随机种子,它能够固定随机数的输出结果:
np.random.seed(0)
np.random.rand()
# 0.5488135039273248
np.random.seed(0)
np.random.rand()
# 0.5488135039273248
随机种子seed括号里的数,顾名思义, 好像就是一个固定的序列集合的种子代号,例如代号0(如:0,1,2,3,4…),中包含一大串随机数,但都是固定的,所以,无论后面怎么random.random,生成的随机数都是seed(0)集合中的随机数。
2. Numpy数组的变形与合并
转置: T
np.zeros((2,3)).T
#array([[0., 0.],
# [0., 0.],
# [0., 0.]])
合并操作: r_, c_
对于二维数组而言, r_ 和 c_ 分别表示上下合并和左右合并:
np.r_[np.zeros((2,3)),np.zeros((2,3))]
#array([[0., 0., 0.],
# [0., 0., 0.],
# [0., 0., 0.],
# [0., 0., 0.]])
np.c_[np.zeros((2,3)),np.zeros((2,3))]
#array([[0., 0., 0., 0., 0., 0.],
# [0., 0., 0., 0., 0., 0.]])
一维数组和二维数组进行合并时,应当把其视作列向量,在长度匹配的情况下只能够使用左右合并的 c_ 操作。
维度变换: reshape
reshape 能够帮助用户把原数组按照新的维度重新排列。在使用时有两种模式,分别为 C 模式和 F 模式,分别以逐行和逐列的顺序进行填充读取。
target = np.arange(8).reshape(2,4)
#array([[0, 1, 2, 3],
# [4, 5, 6, 7]])
target.reshape((4,2), order='C') # 按照行读取和填充
#array([[0, 1],
# [2, 3],
# [4, 5],
# [6, 7]])
target.reshape((4,2), order='F') # 按照列读取和填充
#array([[0, 2],
# [4, 6],
# [1, 3],
# [5, 7]])
特别地,由于被调用数组的大小是确定的, reshape 允许有一个维度存在空缺,此时只需填充-1即可:
target.reshape((4,-1))
#array([[0, 1],
# [2, 3],
# [4, 5],
# [6, 7]])
下面将 n*1 大小的数组转为1维数组的操作是经常使用的:
target = np.ones((3,1))
#array([[1.],
# [1.],
# [1.]])
target.reshape(-1)
#array([1., 1., 1.])
3. np数组的切片与索引
数组的切片模式支持使用 slice 类型的 start????step 切片,还可以直接传入列表指定某个维度的索引进行切片:
target = np.arange(9).reshape(3,3)
#array([[0, 1, 2],
# [3, 4, 5],
# [6, 7, 8]])
target[:-1, [0,2]]#:-1代表从第1行到最后一行,[0,2]代表第0列和第2列
#array([[0, 2],
# [3, 5]])
此外,还可以利用 np.ix_ 在对应的维度上使用布尔索引,但此时不能使用 slice 切片:
target[np.ix_([True, False, True], [True, False, True])]
#array([[0, 2],
# [6, 8]])
target[np.ix_([1,2], [True, False, True])]
#array([[3, 5],
# [6, 8]])
当数组维度为1维时,可以直接进行布尔索引,而无需 np.ix_ :
new = target.reshape(-1)
new[new%2==0]
# array([0, 2, 4, 6, 8])
4. 常用函数
为了简单起见,这里假设下述函数输入的数组都是一维的。
where
where 是一种条件函数,可以指定满足条件与不满足条件位置对应的填充值:
a = np.array([-1,1,-1,0])
np.where(a>0, a, 5) # 对应位置为True时填充a对应元素,否则填充5
# array([5, 1, 5, 5])
nonzero, argmax, argmin
这三个函数返回的都是索引, nonzero 返回非零数的索引, argmax, argmin 分别返回最大和最小数的索引:
a = np.array([-2,-5,0,1,3,-1])
np.nonzero(a)
# (array([0, 1, 3, 4, 5], dtype=int64),)
a.argmax()
# 4
a.argmin()
# 1
any, all
any 指当序列至少 存在一个 True 或非零元素时返回 True ,否则返回 False
all 指当序列元素 全为 True 或非零元素时返回 True ,否则返回 False
a = np.array([0,1])
a.any()
# True
a.all()
# False
cumprod, cumsum, diff
cumprod, cumsum 分别表示累乘和累加函数,返回同长度的数组, diff 表示和前一个元素做差,由于第一个元素为缺失值,因此在默认参数情况下,返回长度是原数组减1
a = np.array([1,2,3])
a.cumprod()
#array([1, 2, 6])
a.cumsum()
# array([1, 3, 6])
np.diff(a)
# array([1, 1])
统计函数
常用的统计函数包括 max, min, mean, median, std, var, sum, quantile ,其中分位数计算是全局方法,因此不能通过 array.quantile 的方法调用:
#target = array([[0, 1, 2],
# [3, 4, 5],
# [6, 7, 8]])
target = np.arange(5)
# array([0, 1, 2, 3, 4])
target.max()
# 4
np.quantile(target, 0.5) # 0.5分位数
#2.0
但是对于含有缺失值的数组,它们返回的结果也是缺失值,如果需要略过缺失值,必须使用 nan* 类型的函数,上述的几个统计函数都有对应的 nan* 函数。
target = np.array([1, 2, np.nan])
#array([ 1., 2., nan])
target.max()
# nan
np.nanmax(target)
# 2.0
np.nanquantile(target, 0.5)
# 1.5
对于协方差和相关系数分别可以利用 cov, corrcoef 如下计算:
target1 = np.array([1,3,5,9])
target2 = np.array([1,5,3,-9])
np.cov(target1, target2)
#array([[ 11.66666667, -16.66666667],
# [-16.66666667, 38.66666667]])
np.corrcoef(target1, target2)
#array([[ 1. , -0.78470603],
# [-0.78470603, 1. ]])
最后,需要说明二维 Numpy 数组中统计函数的 axis 参数,它能够进行某一个维度下的统计特征计算,当 axis=0 时结果为列的统计指标,当 axis=1 时结果为行的统计指标:
target = np.arange(1,10).reshape(3,-1)
@array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
target.sum(0)
#array([12, 15, 18])
target.sum(1)
#array([ 6, 15, 24])
5. 广播机制
广播机制用于处理两个不同维度数组之间的操作,这里只讨论不超过两维的数组广播机制。
标量和数组的操作
当一个标量和数组进行运算时,标量会自动把大小扩充为数组大小,之后进行逐元素操作:
res = 3 * np.ones((2,2)) + 1
#array([[4., 4.],
# [4., 4.]])
res = 1 / res
#array([[0.25, 0.25],
# [0.25, 0.25]])
二维数组之间的操作
当两个数组维度完全一致时,使用对应元素的操作,否则会报错,除非其中的某个数组的维度是 或者 ,那么会扩充其具有 的维度为另一个数组对应维度的大小。例如, 数组和 数组做逐元素运算时会把第一个数组扩充为 ,扩充时的对应数值进行赋值。但是,需要注意的是,如果第一个数组的维度是 ,那么由于在第二维上的大小不匹配且不为 ,此时报错。
res = np.ones((3,2))
#array([[1., 1.],
# [1., 1.],
# [1., 1.]])
res * np.array([[2,3]]) # 第二个数组扩充第一维度为3
#array([[2., 3.],
# [2., 3.],
# [2., 3.]])
res * np.array([[2],[3],[4]]) # 第二个数组扩充第二维度为2
#array([[2., 2.],
# [3., 3.],
# [4., 4.]])
res * np.array([[2]]) # 等价于两次扩充,第二个数组两个维度分别扩充为3和2
#array([[2., 2.],
# [2., 2.],
# [2., 2.]])
一维数组与二维数组的操作
当一维数组 与二维数组 操作时,等价于把一维数组视作 的二维数组,使用的广播法则与【b】中一致,当 且 都不是 时报错。
np.ones(3) + np.ones((2,3))
#array([[2., 2., 2.],
# [2., 2., 2.]])
np.ones(3) + np.ones((2,1))
#array([[2., 2., 2.],
# [2., 2., 2.]])
np.ones(1) + np.ones((2,3))
#array([[2., 2., 2.],
# [2., 2., 2.]])
6. 向量与矩阵的计算
向量内积: dot
a = np.array([1,2,3])
b = np.array([1,3,5])
a.dot(b)
#22
向量范数和矩阵范数: np.linalg.norm
在矩阵范数的计算中,最重要的是 ord 参数,可选值如下:
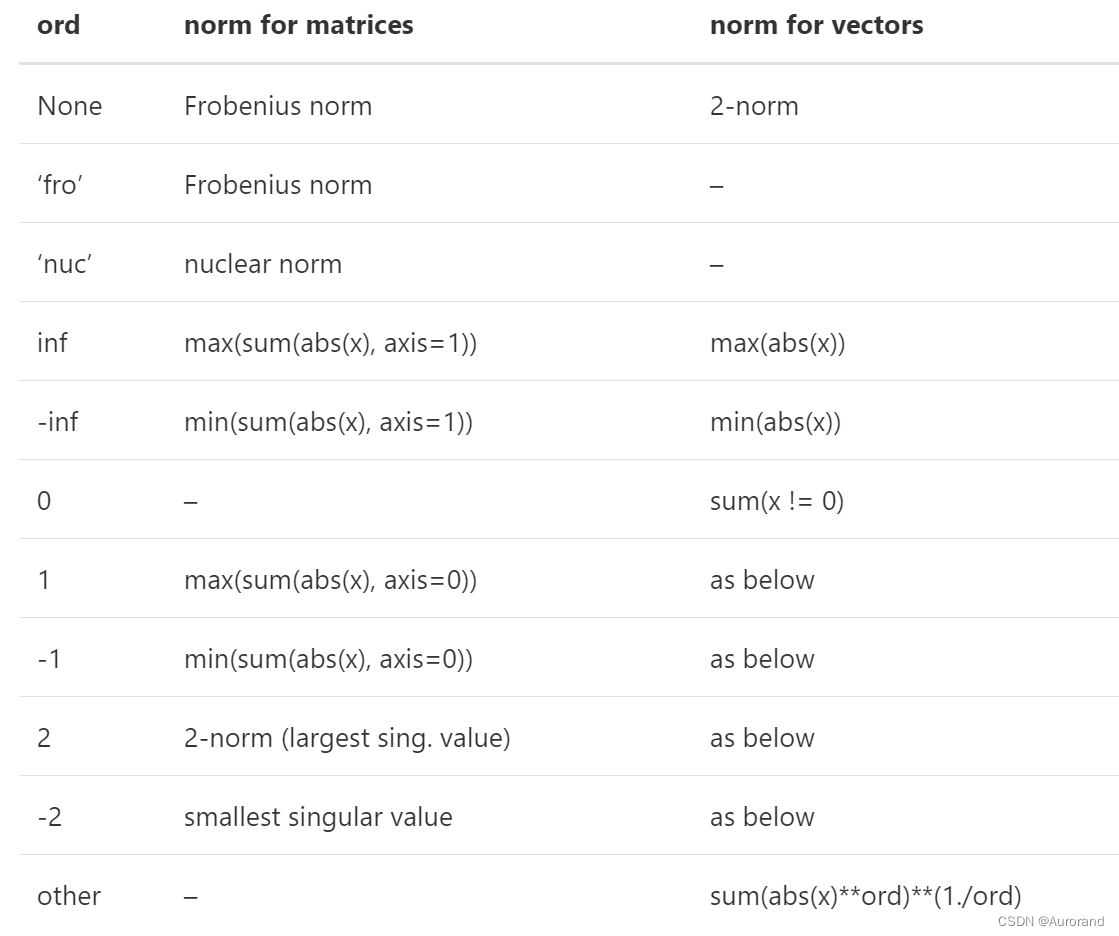
matrix_target = np.arange(4).reshape(-1,2)
#array([[0, 1],
# [2, 3]])
np.linalg.norm(matrix_target, 'fro')
#3.7416573867739413
np.linalg.norm(matrix_target, np.inf)
#5.0
np.linalg.norm(matrix_target, 2)
#3.702459173643833
vector_target = np.arange(4)
# array([0, 1, 2, 3])
np.linalg.norm(vector_target, np.inf)
# 3.0
np.linalg.norm(vector_target, 2)
# 3.7416573867739413
np.linalg.norm(vector_target, 3)
# 3.3019272488946263
矩阵乘法: @
a = np.arange(4).reshape(-1,2)
#array([[0, 1],
# [2, 3]])
b = np.arange(-4,0).reshape(-1,2)
#array([[-4, -3],
# [-2, -1]])
a@b
#array([[ -2, -1],
# [-14, -9]])
最后
以上就是温柔枕头最近收集整理的关于Pandas学习(2)——NumpyNumpy基础的全部内容,更多相关Pandas学习(2)——NumpyNumpy基础内容请搜索靠谱客的其他文章。








发表评论 取消回复