秦路数据分析统计学笔记

分类数据描述统计

频数统计：各分类计数

频数百分比

数值数据描述统计

统计度量：平均数AVERAGE 中位数MEDIAN 众数MODE

                  四分位数quartile（第一分位数25% 第二分位数=50%中位数 第三分位数75%）

                  方差VAR.P 标准差STDEVP 对比数据波动

                  数据标准化Z-Score=(xi-ц均值)/б标准差 压缩后失去量纲意义 仅作数值对比

                  切比雪夫定理：至少有75%的数据，位于平均数2个标准差范围内

                                           至少有89%的数据，位于平均数3个标准差范围内

                                           至少有96%的数据，位于平均数5个标准差范围内

图形：

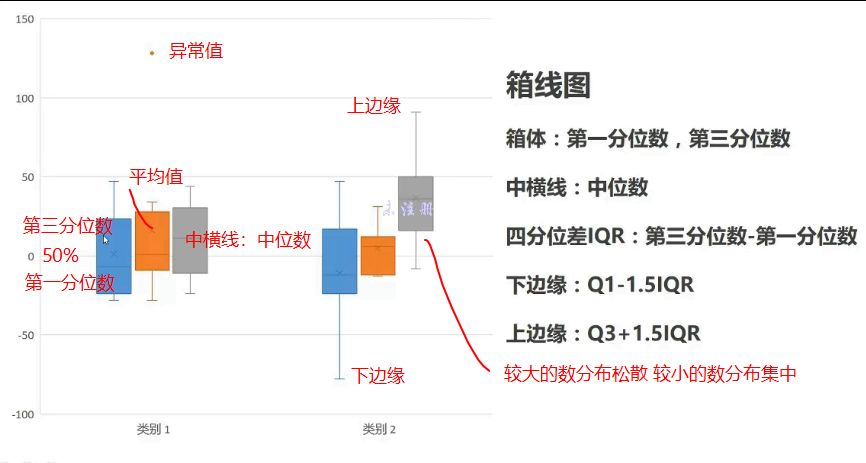
箱线图

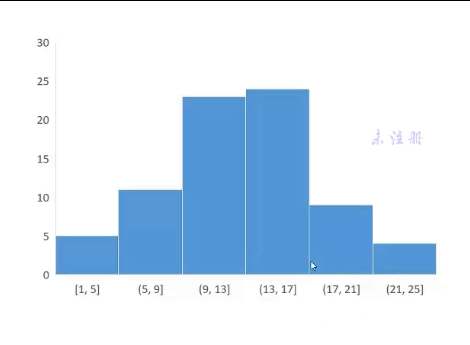
 直方图

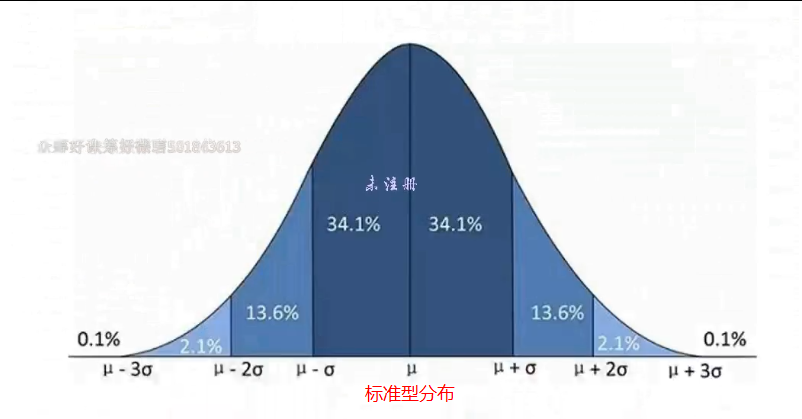
切比雪夫定理2.0：正态分布中，至少有68%的数据，位于平均数1个标准差范围内

                              正态分布中，至少有95%的数据，位于平均数2个标准差范围内

                              正态分布中，至少有99.8%的数据，位于平均数3个标准差范围内

概率-推断统计

条件概率

贝叶斯定理

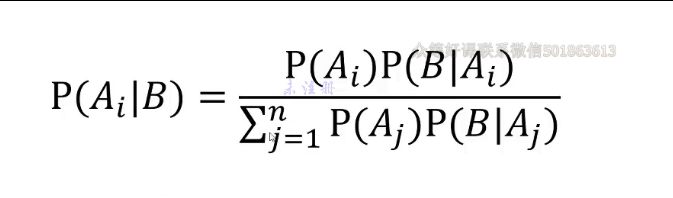
二项分布/伯努利分布

二项分布X~B(n, p)是由伯努利提出的概念，指的是重复n次独立的伯努利实验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立实验中都保持不变，则这一系列试验总称为n重伯努利实验。

N次独立重复实验中发生K次的概率是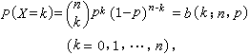

期望：Eξ=np   方差：Dξ=npq

离散型

泊松分布

如果某事件以固定强度λ，随机且独立地出现，该事件在单位时间内出现的次数（个数）可以看成是服从泊松分布。泊松分布适合于描述单位时间内随机事件发生的次数。泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生次数。

概率函数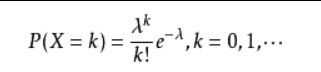

期望=λ   方差=λ

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧20,p≦0.05时，就可以用泊松公式近似得计算。

离散型

正态分布/高斯分布

X~N(μ，σ^2)  当μ = 0,σ = 1时的正态分布是标准正态分布

期望=μ    方差=σ^2   正态分布的期望、均数、中位数、众数相同，均等于μ

正态分布中，至少有68%的数据，位于平均数1个标准差范围内

 正态分布中，至少有95%的数据，位于平均数2个标准差范围内

正态分布中，至少有99.8%的数据，位于平均数3个标准差范围内

假设检验

假设检验是数理统计学中根据一定假设条件由样本推断总体的一种方法。事先对总体参数或分布形式作出某种假设，然后利用样本信息来判断原假设是否成立，采用逻辑上的反证法，依据统计上的小概率原理。常用的假设检验方法有z检验、t检验、卡方检验、F检验等。

https://baijiahao.baidu.com/s?id=1629858003935285309&wfr=spider&for=pc

https://zhuanlan.zhihu.com/p/86178674

显著性水平：一个概率值，原假设为真时，拒绝原假设的概率，表示为 alpha

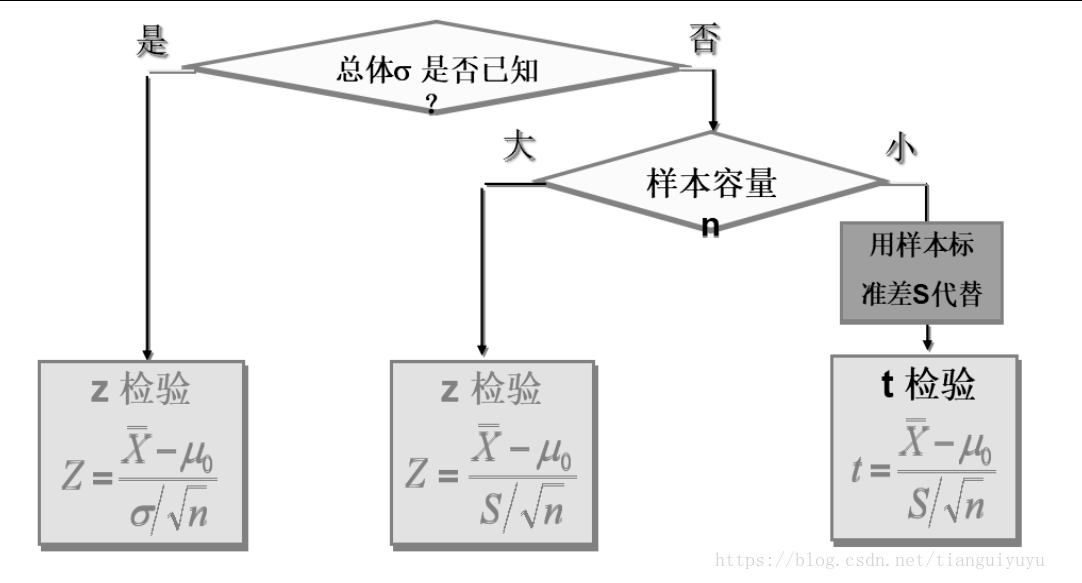
z检验/u检验：一般用于大样本(即样本容量大于30)平均值差异性检验的方法（总体的方差已知）。它是用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著

t检验：主要用于样本含量较小（例如n<30），总体标准差σ未知的正态分布。目的是用来比较样本均数所代表的未知总体均数μ和已知总体均数μ0。实际应用中，T检验可分为三种：单样本T检验、配对样本T检验和双独立样本T检验

f检验：检验两个正态随机变量的总体方差是否相等

卡方检验：检验两个变量之间有没有关系。属于非参数检验，主要是比较两个及两个以上样本率（构成比）以及两个分类变量的关联性分析

https://blog.csdn.net/qq_22592457/article/details/92982170

样本量估计

第一类错误概率/检验水准α：越小所需样本含量越多。对于相同α，双侧检验比单侧检验所需样本更多

第二类错误概率β/检验功效1-β：检验功效越大，第二类错误的概率越小，所需样本含量越多

容许误差λ：容许误差越大，所需样本含量越小

总体标准差θ：总体标准差越大，所需样本含量越多

最后

以上就是成就水杯为你收集整理的秦路数据分析统计学笔记的全部内容，希望文章能够帮你解决秦路数据分析统计学笔记所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。