各种触发器的特性方程_[精品课程] 架空线的状态方程式架空输电线路设计

..................................................

三峡大学以《架空输电线路设计》国家级规划教材为蓝本，汇聚电气工程国家级教学团队、北京道亨时代科技有限公司，面向输电线路工程专业本、专科学生，以及输电行业工程技术人员等社会化学习者，提供线路设计专业资料、法规标准、设计模型、专家咨询、行业培训等优秀教学资源，为我国输电行业的高等教育发展贡献力量。 ..................................................

第26次 精品课程视频

REC

..............................................

..............................................

架空线的线长和弧垂是档距、高差和架空线比载、应力的函数。当气象条件发生变化时，这些参数将会发生变化。气温的升降引起架空线的热膨冷缩，使线长、弧垂、应力发生相应变化。大风和覆冰造成架空线比载增加，应力增大，由于弹性变形使架空线线长增加。不同气象条件(状态)下架空线的各参数之间存在着一定的关系。 揭示架空线从一种气象条件(第一状态)改变到另一种气象条件(第二状态)下的各参数之间关系的方程，称为架空线的 状态方程式 。

..............................................

..............................................

01

基本状态方程式

假设：

(1)架空线为完全弹性体，不考虑长期运行产生的塑性变形，并认为弹性模量E保持不变； (2)架空线为理想柔线，不考虑其刚度的影响； (3)架空线上的荷载均匀分布。

导出：

(1)原始长度L₀：架空线在无应力、制造温度 t₀ 的原始状态下的长度 L₀ 。

(2)悬挂曲线长度L：悬挂于档距为 l，高差为 h 的两悬点 A、B 上，架空线具有气温 t、比载 γ、轴向应力 σ_x，此时悬挂曲线长度 L 。

(3)长度变化的原因：由于温度变化，架空线产生热胀冷缩；由于施加有轴向应力，架空线产生弹性伸长。

设架空线的线性温度膨胀系数为 α，弹性系数为 E ，原始长度的微元 dL₀ ，新的状态下为dL，则

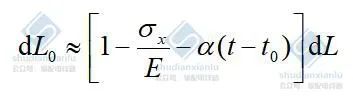
对上式沿架空线线长进行积分

从架空线的悬挂长度L中减去弹性伸长量和温度伸长量，即可得到档内架空线的原始线长。

第一状态:

l₁、h₁、t₁、γ₁、σ₀₁、σ_cp1、L₁

第二状态

l₂、h₂、t₂、γ₂、σ₀₂、σ_cp2、L₂

则两种状态下的架空线悬挂曲线长度折算到同一原始状态下的原始线长相等，所以 得出 基本状态方程式 为: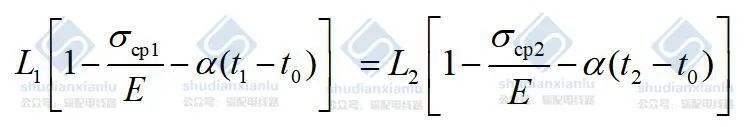

　结论

不同状态下的架空线悬挂曲线长度，折算到原始状态下在原始线长相等。

02

悬链线状态方程式

将线长L、平均应力  σ_cp  的悬链线 线长公式 、平均应力公式(公式见前面第24次课程《架空线的平均高度与平均应力》)代入 基本状态方程式 ，略加整理，就可得到悬挂点不等高时的悬链线状态方程式为

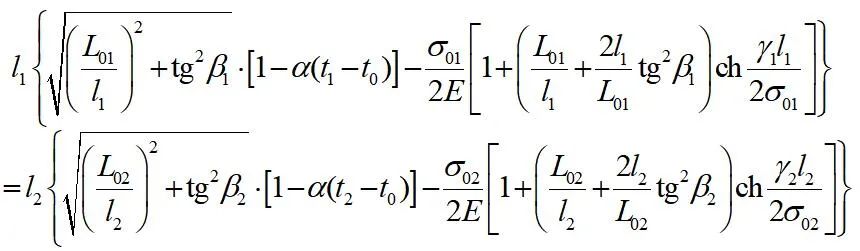
式中:

σ₀₁、σ₀₂   ——  分别为两种状态下架空线弧垂最低点处的应力； l₁、l₂   ——  分别为两种状态下架空线所在平面内的档距； L₀₁、L₀₂   ——  分别为两种状态下不考虑高差(即令h₁=0、h₂=0)时的架空线线长，其值可由计算； β₁、β₂   ——  分别为两种状态下架空线所在平面内的高差角。tgβ₁=h₁/l₁，tgβ₂=h₂/l₂； t₁、t₂   ——  分别为两种状态下的温度；

 t₀   ——  架空线的制造温度。一般取t₀=15℃。

　悬点等高时，h₁=0、h₂=0，tgβ₁=0、tgβ₂=0，则上式变为

 需要考虑风荷载时，可将以上两式中的各参数代以风偏平面内的参数，得到有风时的悬链线状态方程式，感兴趣的读者可自行导出。

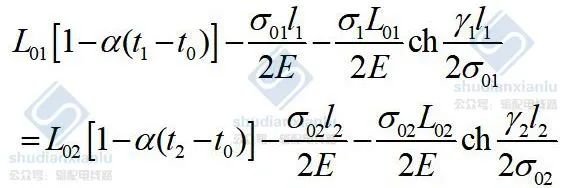
悬链线状态方程式比较复杂，仅适用于计算机求解，其结果通常作为精确值去评价其它近似公式的精度。

03

斜抛物线状态方程式

将斜抛物线线长L及平均应力 σ_cp  代入 基本状态方程式，可得到架空线斜抛物线形式的状态方程式为

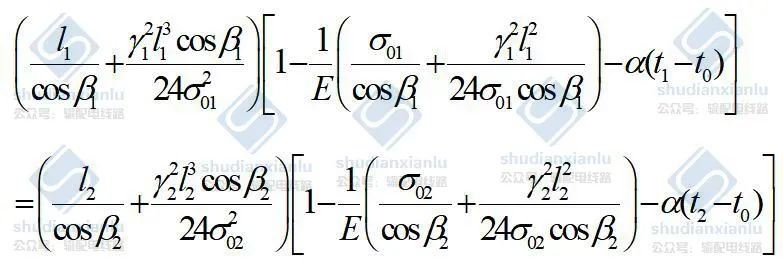
　若档距、高差的大小可认为不变，即l₁=l₂=l、h₁=h₂=h(β₁=β₂=β)时，将上式展开并加以整理后得

计算分析表明，上式中右端各项的结果与左端各项相比可忽略不计，则有

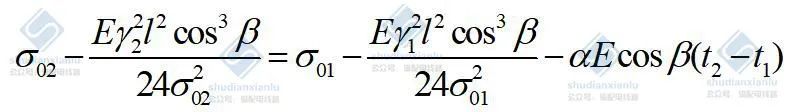
式中 ：

σ₀₁、σ₀₂—分别为两种状态下架空线弧垂最低点处的应力；

γ₁、γ₂—分别为两种状态下架空线的比载；

t₁、t₂−−分别为两种状态下架空线的温度；

 l、β−−分别为该档的档距和高差角；

α、E−−分别为架空线的温度膨胀系数和弹性系数。

此式是斜抛物线状态方程式的近似式，但近似过程弥补了斜抛物线公式的误差，因此精度很高。对于重要跨越档或高差很大的档距，也能够满足工程要求，成为最常用的不等高悬点架空线状态方程式，通常就称为斜抛物状态方程式，或简称为状态方程式。

❀ 状态方程式主要用途：

利用状态方程式，可由状态Ⅰ的参数 l₁、h₁(或 β₁ )、γ₁、σ₀₁、t₁，计算状态Ⅱ 的参数 l₂、h₂(或 β₂ )、γ₂、σ₀₂、t₂ 中的任意一个，一般是求取应力 σ₀₂ 。但是悬链线状态方程式比较复杂，仅适用于计算机求解，其结果通常作为精确值去评价其它近似公式的精度。

3.1 等高悬点的斜抛物线状态方程式

令 斜抛物状态方程式 中的β=0，就得到等高悬点的斜抛物线状态方程式

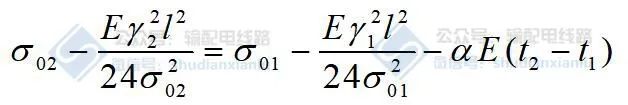
3.2 档距中央轴向应力的状态方程式

斜抛物状态方程式 两端除以 cosβ，并注意到档距中央架空线轴向应力的计算式，得

结论：

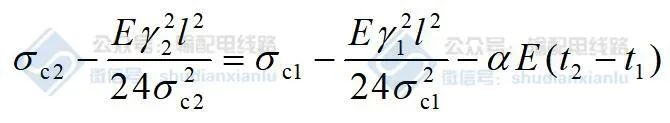
若以架空线中央应力代替最低点应力，则不等高悬点和等高悬点架空线的斜抛物线状态方程式具有相同的形式。换句话讲，架空线中点应力的斜抛物线状态方程式消除了高差的影响，使计算简化。 

3.3 有风时的斜抛物线状态方程式

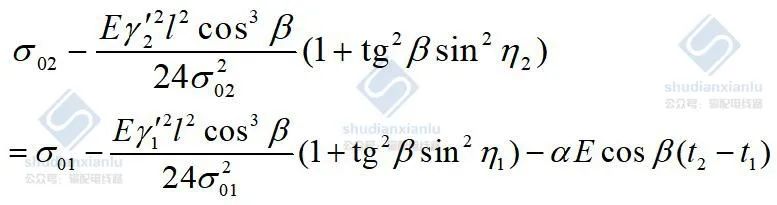
式中 ：

η ₁、η ₂—分别为两种状态下架空线的风偏角。

γ’₁、γ’₂—分别为两种状态下架空线的综合比载。

注意：

虽然式中 γ’₁、γ’₂  均为综合比载，但σ₀₁、σ₀₂仍为架空线顺线路方向的水平应力分量，即垂直平面内的最低点应力，不能把σ₀₁、σ₀₂误认为风偏平面内架空线最低点的应力。当利用上式求出有风状态下顺线路方向的水平应力σ₀₂后，欲想知道风偏平面内架空线最低点的应力或悬挂点应力，需将σ₀₂代入 均布垂直比载和水平比载共同作用下架空线的计算 专题中介绍的习惯公式求得。

输配电线路  公众号  编辑

输配电线路  公众号  编辑

课程章节

(点击以下目录自动进入相应章节学习) 第一章 绪论 1.1 输电线路及其分类 1.2 输电线路的组成部分 第二章 架空输电线路的基本知识 2.1 架空线的材料、种类和用途 2.2 导线截面的选择 2.3 地线架设的相关规定 2.4 绝缘子及其设计 2.5 金具的种类 2.6 杆塔、基础与接地 2.7 导线的排列方式和换位 第三章 设计用气象条件 3.1 气象三要素及其资料收集 3.2 气象条件的重现期和最大设计风速的确定 3.3 覆冰厚度与气温的选取 3.4 各种气象条件的组合 第四章 架空线的机械物理特性和比载 4.1 架空线的机械物理特性 4.2 许用应力和安全系数 4.3 七个比载及其求解 第五章 均布荷载下架空线的计算 5.1 架空线悬链线方程的积分普遍形式 5.2 等高悬点架空线的悬挂曲线方程 5.3 等高悬点架空线的弧垂、线长和应力 5.4 等高悬点架空线计算举例 5.5 不等高悬点架空线的弧垂、线长和应力 5.6 不等高悬点架空线的计算举例 5.7 架空线计算公式的简化 5.8 架空线的平均高度与平均应力 5.9 均布垂直比载和水平比载共同作用下架空线的计算 (持续更新中......)

授课老师

孟遂民

主讲教师：

唐波、孟遂民、黄力、张子引、吴鹏 在线免费网课，请在本文底部，点击“原文阅读”进入免费学习。 认证学习，可以获得权威认证证书。 —我已酷酷结束—