本文属于「离散数学」系列文章之一。这一系列着重于离散数学的学习和应用。由于内容随时可能发生更新变动，欢迎关注和收藏离散数学系列文章汇总目录一文以作备忘。此外，在本系列学习文章中，为了透彻理解数学知识，本人参考了诸多博客、教程、文档、书籍等资料。以下是本文的不完全参考目录，在后续学习中还会逐渐补充：

• 离散数学及其应用 第七版 Discrete Mathematics and Its Applications 7th ，作者是 Kenneth H.Rosen
• 离散数学 第二版，武波等编著，西安电子科技大学出版社

由【离散数学】数理逻辑 第一章 命题逻辑(4) 联结词的完备集知，所有命题公式均可由 $\neg ,\wedge ,\vee$ 表示。又由【离散数学】数理逻辑 第一章 命题逻辑(3) 逻辑等价与蕴含知，大部分逻辑等价式都是成对出现的，不同的只是 $\wedge ,\vee$ 互换、$T,F$ 互换——公式的这种特征被称为对偶，两个等价的命题公式分别对偶后仍然等价就是对偶原理：

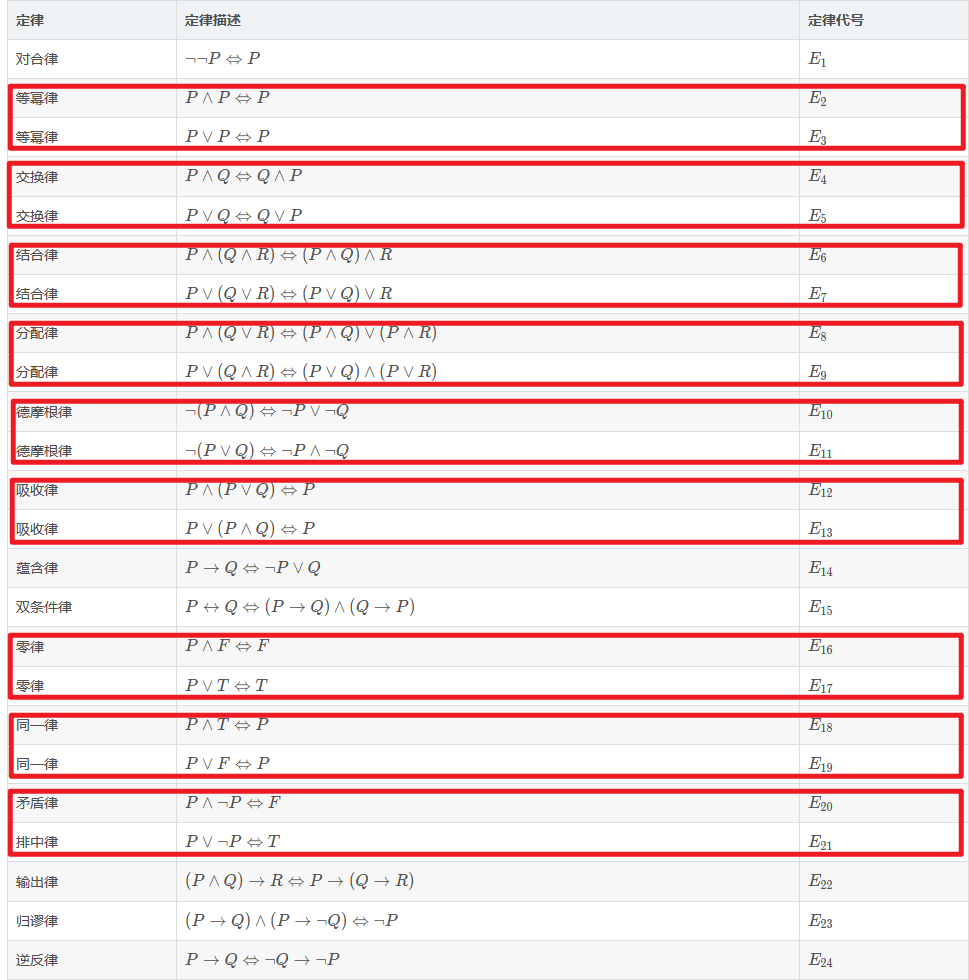
5. 对偶式

5.1 对偶公式

定义5.1：设有命题公式 $A$ ，其中仅含有联结词 $\wedge ,\vee ,\neg$ ，在 $A$ 中将 $\wedge ,\vee ,T,F$ 分别替换为 $\vee ,\wedge ,F,T$ ，得公式 $A^{\ast }$ ，则 $A^{\ast }$ 称为 $A$ 的对偶 dual 公式。

显然，$(A^{\ast }{)}^{\ast }=A$ ，即对偶是相互的。例如，$P\vee (Q\wedge R)$ 与 $P\wedge (Q\vee R)$ 互为对偶。

例1：写出下列各式的对偶公式。
(1) $(P\vee Q)\wedge R$
(2) $(P\wedge Q)\vee T$
(3) $P\uparrow Q$
解答：(1) $(P\wedge Q)\vee R$；(2) $(P\vee Q)\wedge F$；(3) 因为与非 $P\uparrow Q\iff \neg (P\wedge Q)$ ，所以对偶公式为 $\neg (P\vee Q)\iff P\downarrow Q$ 。

定理5.1：设 $A$ 与 $A^{\ast }$ 是对偶公式，其中仅含有联结词 $\neg ,\wedge ,\vee$，$P_1,P_2,\dots ,P_n$ 是出现于 $A$ 和 $A^{\ast }$ 中的所有命题变元，于是：
$$\begin{gathered} \neg A(P_1,P_2,\dots ,P_n)\iff A^{\ast }(\neg P_1,\neg P_2,\dots ,\neg P_n) \\ A(P_1,P_2,\dots ,P_n)\iff \neg A^{\ast }(\neg P_1,\neg P_2,\dots ,\neg P_n) \end{gathered}$$
证明这一定理需要使用归纳法，将在【离散数学】集合论 第三章 集合与关系(4) 集合的归纳定义、归纳证明、数学归纳法第一/二原理中加以说明。

直观地来看，这一定理潜在地揭示了对偶与德摩根律的联系——对偶中变换了 $\wedge$ 和 $\vee$、$T$ 和 $F$ ，相比德摩根律只缺了否定命题变元这一步。下面以一个例子 $A(P,Q,R)\iff \neg P\vee (Q\wedge R)$ 加以说明：
$$\begin{array}{rl}\neg A(P,Q,R)& \iff \neg (\neg P\vee (Q\wedge R))\\ & \iff P\wedge \neg (Q\wedge R)\\ & \iff P\wedge (\neg Q\vee \neg R)\\ A^{\ast }(P,Q,R)& \iff \neg P\wedge (Q\vee R)\\ A^{\ast }(\neg P,\neg Q,\neg R)& \iff \neg (\neg P)\wedge (\neg Q\vee \neg R)\\ & \iff P\wedge (\neg Q\vee \neg R)\end{array}$$

5.2 对偶原理

定理5.2：设 $A,B$ 为仅含有联结词 $\wedge ,\vee ,\neg$ 的命题公式，$P_1,P_2,\dots ,P_n$ 是出现在 $A$ 和 $B$ 中的命题变元，则有：
（1）如果 $A\iff B$ ，则 $A^{\ast }\iff B^{\ast }$ 。
（2）如果 $A\Rightarrow B$ ，则 $B^{\ast }\Rightarrow A^{\ast }$ 。
本定理被称为对偶原理，在很多常用的逻辑等价式中均有体现。

证明：
（1）$A\iff B$ 意味着 $A(P_1,P_2,\dots {,}_n)\leftrightarrow B(P_1,P_2,\dots ,P_n)$ 永真，所以 $\neg A(P_1,P_2,\dots {,}_n)\leftrightarrow \neg B(P_1,P_2,\dots ,P_n)$ 永真。

由定理5.1知：
$$\begin{gathered} \neg A(P_1,P_2,\dots ,P_n)\iff A^{\ast }(\neg P_1,\neg P_2,\dots ,\neg P_n) \\ \neg B(P_1,P_2,\dots ,P_n)\iff B^{\ast }(\neg P_1,\neg P_2,\dots ,\neg P_n) \end{gathered}$$

所以 $A^{\ast }(\neg P_1,\neg P_2,\dots ,\neg P_n)\leftrightarrow B^{\ast }(\neg P_1,\neg P_2,\dots ,\neg P_n)$ 永真。 再运用代入规则，以 $\neg P_i$ 代替 $P_i$（$1\le i\le n$），得到 $A^{\ast }(P_1,P_2,\dots ,P_n)\leftrightarrow B^{\ast }(P_1,P_2,\dots ,P_n)$ 永真，从而 $A^{\ast }\iff B^{\ast }$ 。

（2）$A\Rightarrow B$ 意味着 $A(P_1,P_2,\dots {,}_n)\to B(P_1,P_2,\dots ,P_n)$ 永真。所以由逆反律 $E_{24}$ 知 $\neg B(P_1,P_2,\dots {,}_n)\to \neg A(P_1,P_2,\dots ,P_n)$ 永真。

再由定理5.1知，$B^{\ast }(\neg P_1,\neg P_2,\dots ,\neg P_n)\to A^{\ast }(\neg P_1,\neg P_2,\dots ,\neg P_n)$ 永真。使用代入规则，以 $\neg P_i$ 代替 $P_i$（$1\le i\le n$），得到 $B^{\ast }(P_1,P_2,\dots ,P_n)\to A^{\ast }(P_1,P_2,\dots ,P_n)$ 永真，从而 $B^{\ast }\Rightarrow A^{\ast }$ 。

上述两个证明，也可以先运用代入规则，用 $\neg P_i$ 代替 $P_i$ ，再使用定理5.1，最终得到的结论完全一致，而且证明过程更简单。

最后

以上就是寒冷玫瑰为你收集整理的【离散数学】数理逻辑 第一章 命题逻辑(5) 对偶式、对偶原理5. 对偶式的全部内容，希望文章能够帮你解决【离散数学】数理逻辑 第一章 命题逻辑(5) 对偶式、对偶原理5. 对偶式所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。