决策树与回归树区别到底在哪

前面讲了几节决策树从底层的构造原理，更多的是面向分类的决策树，从树的用途上讲还有一种用途，那就是回归树，结构也是树，但是出来的结果是回归值。可能很多人不用回归树做任务的时候很少去管回归树，以至于有时候也不知道它们的区别，但是还是有必要掌握，因为牛逼的树算法，比如GBDT，xgboost的单棵树可不是分类树，是回归树。

所谓分类树就是面向分类的，每个决策树最末端的叶子结点出来的是一个分类标签，不是0就是1或者2等类别。回归树就是面向回归的，回归就是拟合函数一样，输出连续值，比如根据一大堆当天的特征输出明天的气温，气温是每个样本唯一输出的值，只不过输出的值根据特征的不一样输出值不一样而已，但是它们输出的意义是一样的，那就是都是气温。搞清楚这两者的输出区别很重要。

再来简单回顾下决策树的历程，对于分类树，最开始以信息熵的方式作为特征分裂节点的选择，是第一代ID3方法，之后改进信息熵的部分缺点，采用信息增益的方式作为分类节点，变成了C4.5方法，再有就是采用gini系数的方式作为特征分裂的方法，变成了CART分类树，但是gini系数的方法更多见于回归树里面，此时回归分类已经有点混用了。

CART的字面意思就是分类和回归树(classification and regression tree)。关于分类树就不再介绍了。重点解释下回归树的构造与区别。

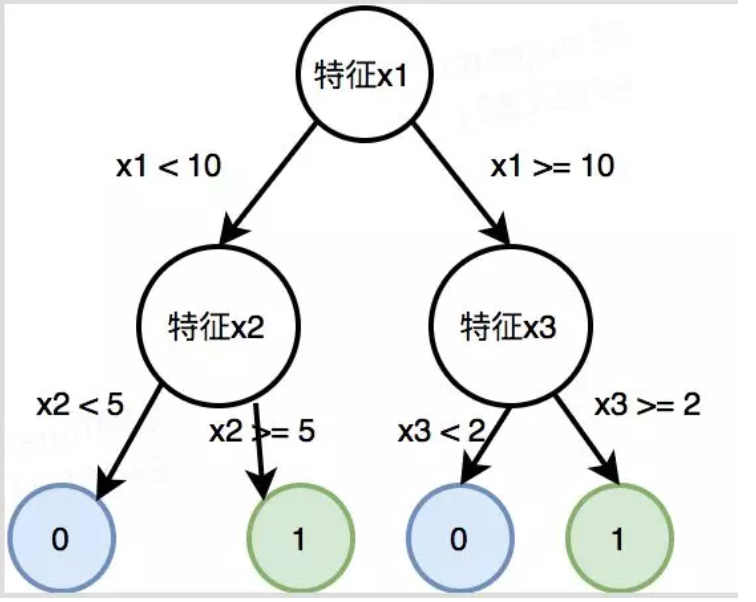
我们说分类树的最后一层叶子结点后才是分类标签，其他时候的节点都不是，可以认为是某个特征属性。简单如图1所示，树构建完以后就是父节点都是按照大特征走，走到最后才是分类结果。

那么回归树不是这样，它们所有节点可以理解为都是一个东西，就是待回归属性，比如温度，最后的回归值是把树走完走到最后一个节点的值。简单如图2所示：

可以看到，分支的条件基本不变，都是某个特征按照条件走对应分支。上图的意思就是，给一组样本特征（x1,x2,x3），假如你什么都不干，那回归的输出值就是50，加入按照x1走一步，可能回归得到30度或者80度，如果你不往下走了，那这就是最终的回归值，如果还往下走，那就再对应属性走，得到最后的回归温度值。

所以在理解上一个很明显的区别就是，回归树，每一个节点都可以认为是一个回归值，只不过这个值不是最优回归值，只有最底层的节点回归值可能才是理想的回归值。所谓回归，也是走到节点的尽头，看看这个节点值是多少，那就把它当成输出值吧。

到了这里，你去套用一下分类树的构造方法去建树，你会发现没办法了，回归树节点不是属性特征呀，是一个具体的值呀，不像分类树是一个属性。说不是属性，也不完全是，要不然你怎么知道是按照x1属性分裂的呢，所以如果把回归树画成下面这样的更好理解：

一个节点有两个东西，有回归值（蓝色），也有分裂选择的属性（浅绿色）。这样来了一组特征，我就知道最终怎么去回归以及回归得到的值是多少了。

说了半天我们只是在说回归树建完后的样子，那么如何去建这样的一个回归树呢？

其实建回归树和建分类树有相似也有不同，相似处在于：每个节点需要知道两个分裂的东西，一个是特征属性，是x1还是x2去分裂，另外一个是加入选择了x1去分裂，那么按照多少分裂左右两边合适（也就是图中的10是怎么来的）。至于每个节点的回归值怎么来的，等会再说。

这两个东西怎么来的呢？很简单，粗暴的遍历，和分类树一样，遍历所有特征(X1～Xn)，每个特征再去遍历所有的分割点，这在前面也讲过，应该知道。所以你去看源码会发现，在某个地方一定有这样的两层for循环去遍历寻找这样的分割属性与对应的分割值，或者就是改进的两层for循环。

那么现在另外一个重要的问题就是，你怎么判断特征x1分裂值10和特征x3分裂值2在这个节点构建上的好坏呢？对回归树用平方误差最小化准则，对分类树用基尼指数最小化准则，进行特征选择，生成二叉树。

首先我们说说顶节点50是怎么来的，还是以温度为例，那么50就是在当前集合里所有样本的温度的平均值，此时没有分裂，集合就是所有样本。那么假如按照(x1,10)分裂，也就是图中的那样，是不是会有两个子集了，这样，是不是也可以计算每个子集里面的平均温度作为这个集合的回归值（也就是30，80），同理(x3,2)在第一个节点的时候也可以分裂，可能也会有个子节点的平均值，假设（20，70）吧，那么到底(x1,10)好还是(x3,2)好呢，一个重要的损失函数来了，那就是平方损失函数：Loss(y,f(x))=(f(x)−y)2 ； （当然也有其他的函数）

经过分裂的两个子集分别可以计算一个这样的损失值，y就是对应子集平均值，对应图中就是第二层节点的30那个值，而f(x)就是对应子集里面每一个样本实际用于训练的真实温度吧。这样左右子集都可以计算一个损失值，加起来就是分裂方式(x1,10)的损失值，同理可以计算(x3,2)以及任何一个分裂方式的值。最后挑选最小损失值对应的分裂方式就是当前节点的分裂方式。一旦分裂方法固定后，就可以得到对应的左右子集了，那么也就可以计算对应子集的平均值作为该节点的回归值了。

也许你会问，这么做合理吗？我们想一下，这样做类似什么算法？是不是很像聚类一样？每一个节点的值就是对应子集的均值，想想kmeans聚类的目标函数是什么，也是平方损失函数吧。既然类似聚类，一个样本想得到好的回归值，是不是在各个特征上聚到和自己最像的样本上是不是最合理。这么一看，回归树其实是一种更高级的聚类方法，回归值是聚类的中心值。只不过这是一种高级的非线性的聚类。

下图是统计学习方法上回归树的算法流程图，请好好对比上述的文字过程理解下，还是非常容易懂的。

至此我想你应该理解了到底什么是分类树，什么是回归树了，它们之间有区别也有共性，典型的区别在于，回归树输出连续值，节点裂变的损失函数或者方法不一样。共性在于，都存在着分裂节点属性以及属性值的选择问题。

回归树是更高级算法GBDT、Xgboost的基础部分，留着下节再来介绍。

更多文章关注公号获取：

最后

以上就是鳗鱼水池为你收集整理的决策树与回归树区别到底在哪的全部内容，希望文章能够帮你解决决策树与回归树区别到底在哪所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。