【区间dp】关路灯牛客网题解

83 阅读 0 评论 55 点赞

我是靠谱客的博主重要麦片，最近开发中收集的这篇文章主要介绍【区间dp】关路灯牛客网题解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

链接：https://ac.nowcoder.com/acm/contest/93/J?&headNav=www
来源：牛客网
注：我提交的时候，后台判题程序有问题，java没法AC，实际上代码是没问题的。

时间限制：C/C++ 2秒，其他语言4秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

我国现在能源消耗非常严重，现在政府有这样一个工作，每天早上都需要把一些路灯关掉，
但是他们想让在关闭的过程中所消耗的能源是最少的，负责路灯关闭的工作人员以1m/s的速度进行行走，
假设关闭路灯的时候不需要花费任何的时间，请你编写一个程序，计算在给定路灯位置和每个路灯的消耗能源的多少，
求出当所有路灯关闭的时候所需要的最少能量

输入描述:

多组测试数据循环输入
每组测试数据第一行：N表示路灯的数量 （2<=N <=1000）
第二行：V表示开始关灯的路灯号码。 （1<=V<=N）
接下来的N行中，每行包含两个用空格隔开的整数D和W，用来描述每盏灯的参数
D表示该路灯到原点的距离 (用米为单位来表示)，
W表示灯泡的功率，即每秒该灯泡所消耗的能量数。（0<=D<=1000，0<=W<=1000）
路灯按照顺序给出，起始位置的那盏灯不算消耗的电能里面
输出描述:
输出一个整数，即消耗能量之和的最小值。

示例1
输入

输出

说明
对于样例，我一开始在第三个路灯的位置，即在6位置
第1s的时候去5把第二盏灯关闭，消耗电能8
然后去第四盏灯，第四盏灯亮的时间是4s 所以消耗电能28
最后去关第一盏灯第一盏灯亮的时间是10s 所以消耗电能20
最后总和为8+28+20=56

分析：
定义dp[i][j]。
将数组分为三部分，最中间的是处理过的，那么肯定右两个指针分割它们，那么，dp[i][j]的意义为
已经处理过的部分[i,j]，消耗的最小能源值是多少。
从图上可以看出来，二维表dp[i][j]还需要保存工作人员当前的位置。
则设置dp[i][j][2],同样可以看成二维dp表，即一个单元格存两个数，这样好理解。
工作人员每次去往下一个地方，就是i和j向左右扩展，并且工作人员当前要嘛在i处，要吗在j处,即dp[i][j][0]表示在左边，dp[i][j][1]表示在右边。
在这里插入图片描述
每次去往下一个地方花的时间算出来，乘以[1,i-1]以及[i+1,N]上的功率总和。就是浪费的时间。
W[i]重新定义为1到i上的功率总和。
用来加速求一个段上的总和，比如总和[1,i]就是W[i]，总和[i+1,N],就是W[N]-W[i]
显然，最开始的时候当前位置即可以看作在左边，也可以看作在右边，那么的dp[V][V][0]=dp[V][V][1]=0
最终结束的位置是dp[1][N][0]和dp[1][N][1]。
画表后得知，三个条件，画三条红线，i<=V,j>=V,且i<j,可知只需对右上角的小正方形做dp即可（其左底角位置为[V][V]）。
状态依赖：
举个例子：dp[i][j][0]表示中间处理好的一段为i到j,现在工作人员在左边，那么它可能是工作人员在右边走过来的，即由dp[i][j-1][1]转移过来的，也可能是一直都在左边，就是又往左走了一步，即由dp[i+1][j]转移过来的。
其他情况分析后和这个都是一样的。
状态依赖为dp[i][j]依赖dp[i+1][j]和dp[i][j-1]。可知每个单元格依赖它下面的和左边的，即从下到上，从左往右dp即可。
其中的具体转移看代码dp主体，回归题意就能看懂，其中抠细节比较费时间。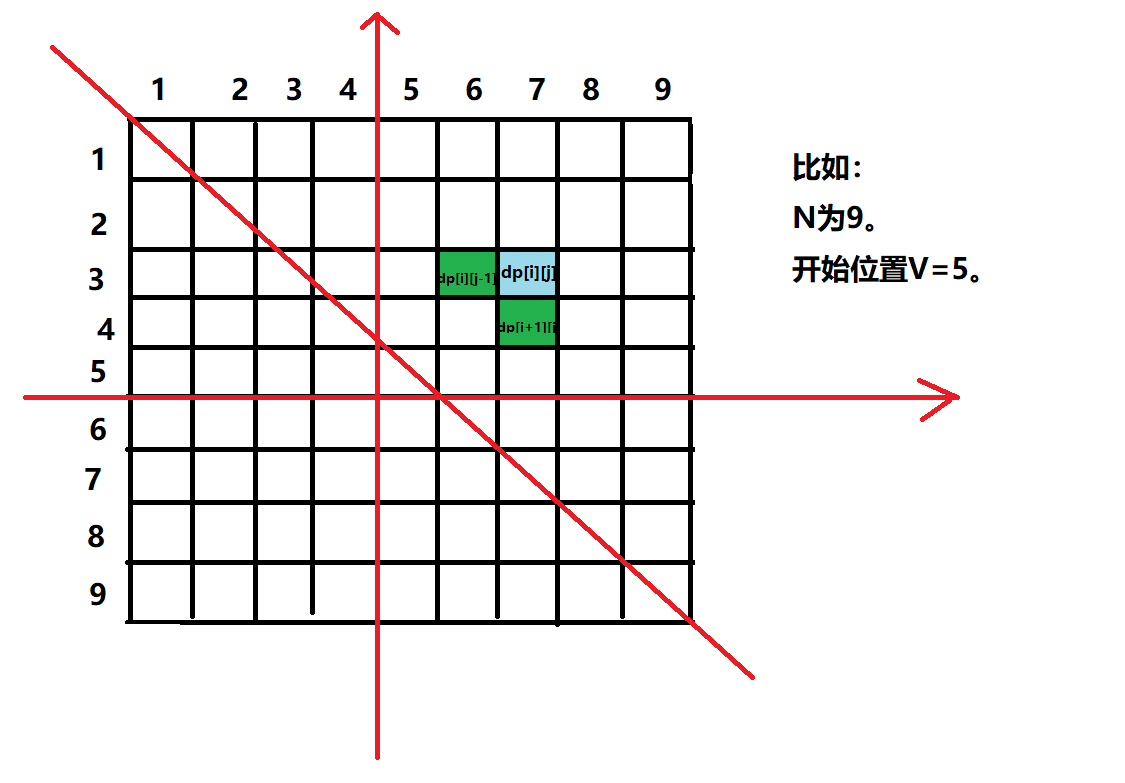在这里插入图片描述
填写初始dp
那么，需要填写base case，即第V行的前V个，和第V列的前V个
第V列从下往上时，dp只依赖于它下面的，根据意义可知，它下面的单元格j是固定为V的，回归到题意，说明一次也不能往右移动，每次都只能往左移动
所以dp[i][V][0]是如何求的，很容易理解
而dp[i][V][1]怎么求呢，很简单，dp[i][V][0]变为dp[i][V][1],意思就是从这头跑到那头，不关任何灯。
上代码：

import java.util.*;
/**
 * @author week
 * @Title: Turn_off_the_street_lights
 * @ProjectName algorithm
 * @Description: TODO
 * @date 2019/6/1216:04
 */
public class Turn_off_the_street_lights {
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        while (sc.hasNext()){
            int N=sc.nextInt();
            int V=sc.nextInt();
            int D[]=new int[N+1];
            int W[]=new int[N+1];
            for(int i=1;i<=N;i++){
                D[i]=sc.nextInt();
                W[i]=sc.nextInt();
                W[i]+=W[i-1];
            }
            long dp[][][]=new long[N+1][N+1][2];
            for(int i=V-1;i>0;i--){
                dp[i][V][0]=dp[i+1][V][0]+(D[i+1]-D[i])*(W[i]+W[N]-W[V]);
                dp[i][V][1]=dp[i][V][0]+(D[V]-D[i])*(W[i-1]+W[N]-W[V]);
            }
            for(int i=V+1;i<=N;i++){
                dp[V][i][1]=dp[V][i-1][1]+(D[i]-D[i-1])*(W[V-1]+W[N]-W[i-1]);
                dp[V][i][0]=dp[V][i][1]+(D[i]-D[V])*(W[V-1]+W[N]-W[i]);
            }
            //写不写都行，dp[V][V][0]=dp[V][V][1]=0;
            for(int i=V-1;i>0;i--){
                for(int j=V+1;j<=N;j++){
                    dp[i][j][0]=Math.min(dp[i+1][j][1]+(D[j]-D[i])*(W[i]+W[N]-W[j]),dp[i+1][j][0]+(D[i+1]-D[i])*(W[i]+W[N]-W[j]));
                    dp[i][j][1]=Math.min(dp[i][j-1][0]+(D[j]-D[i])*(W[i-1]+W[N]-W[j-1]),dp[i][j-1][1]+(D[j]-D[j-1])*(W[i-1]+W[N]-W[j-1]));
                }
            }
            System.out.println(Math.min(dp[1][N][0],dp[1][N][1]));
        }
    }
}