决策树学习通常包括3个步骤：

• 特征选择
• 决策树的构造
• 决策树的剪枝

1. 决策树模型（以分类树为例）

分类决策树是一种描述分类的树形结构，旨在基于经验对目标分类做出判断。

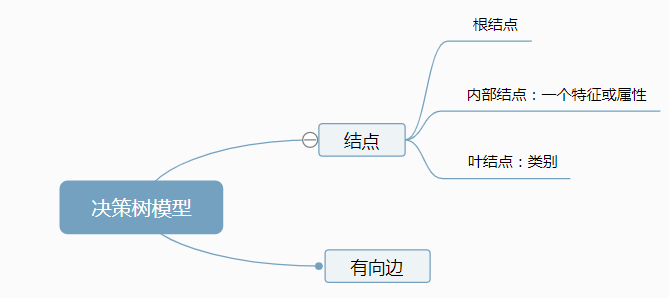
图片来源:https://www.zybuluo.com/rianusr/note/1160843

2. 决策树学习

• 构造
• 剪枝

2.1 构造

构造就是生成一颗完整的决策树。在构造决策树的过程中，需要选择节点的属性，因此，构造需要解决的问题如下：

• 选择哪个属性作为根结点
• 选择哪些属性作为内部结点
• 什么时候停止并生成叶结点

构造决策树，选择结点属性，可依据数据的纯度做出划分，每次划分时选择纯度最高的属性作为结点。

2.2 剪枝

剪枝是为了防止过拟合现象的发生，可分为：

• 预剪枝：在决策树构造时就进行剪枝。
• 后剪枝：在生成决策树后进行剪枝。方法是从叶结点开始，逐层向上对每个结点进行评估。

3. 特征选择的标准

3.1 纯度

纯度可以理解为数据间相似的程度，在分类树决策中可作为划分的依据（希望分类的纯度越高越好）。

3.2 信息熵

信息熵表示信息的不确定度。
在信息论中，随机离散事件出现的概率存在不确定性。随机变量X的熵定义为：
$H(X)=-\begin{array}{c}{\sum }_{i=0}^n{p}_{i}log{p}_i\end{array}$.

3.3 条件熵

$H(Y|X)=\begin{array}{c}{\sum }_{i=1}^n{p}_{i}H(Y|X=X_i)\end{array}$

3.4 信息增益(information gain)

• 信息增益表示得知特征 X 的信息而使类Y的信息的不确定性减少的程度。

• 特征 A 对训练数据集 D 的信息增益 g(D, A），定义为集合D的经验熵 H(D) 与特征 A 给定条件下 D 的经验条件熵 H(D|A) 之差，即：
  $g(D,A)=H(D)-H(D|A)$
  经验熵 H(D) 表示对数据集 D 进行分类的不确定性，而经验条件熵 H(D|A) 表示特征 A 给定的条件下对数据集 D 进行分类不不确定性，因此信息增益可以理解为，在已知特征 A 的条件下，对数据集 D 的分类的不确定性的减少程度。

• 根据信息增益准则的特征选择方法是：对训练数据集 D ，计算其每个特征的信息增益，选择信息增益最大的特征。

• 设训练数据集为 D ，|D| 表示其样本容量。设有 K 个类 $C_k,k=1,2,...,K$，$|C_k|$ 为属于类 $C_k$ 的个数，$\begin{array}{c}{\sum }_{k=1}^K|C_k|\end{array}=|D|$.设特征 A 有 n 个不同的取值，根据特征 A 的取值将 D 划分为 n 个子集$D_1,D_2,...,D_n$, $|D_i|$ 为 $D_i$ 的样本个数 , $\begin{array}{c}{\sum }_{i=1}^n|D_i|\end{array}=|D|$.记子集 $D_i$ 中属于类 $C_k$ 的样本集合为 $D_{i}k$, $|D_{ik}|$ 为 $D_{ik}$ 的样本个数 , 于是信息增益的算法如下：
  【信息增益的算法】
  输入：训练数据集 D 和特征 A；
  输出：特征 A 对训练数据集 D 的信息增益 g(D, A).
  （1）计算数据集 D 的经验熵 H(D):
  $H(D)=-\begin{array}{c}{\sum }_{k=1}^K\frac{|C_k|}{|D|}lo{g}_2\frac{C_k}{D}\end{array}$
  （2）计算特征 A 对数据集 D 的经验条件熵 H(D|A):
  $H(D|A)=\begin{array}{c}{\sum }_{i=1}^n\frac{|D_i|}{|D|}H(D_i)\end{array}$=-$\begin{array}{c}{\sum }_{i=1}^n\frac{|D_i|}{|D|}\end{array}\begin{array}{c}{\sum }_{k=1}^K\frac{|D_{ik}|}{|D_i|}lo{g}_2\frac{|D_{ik}|}{|D_i|}\end{array}$
  （3）计算信息增益
  $g(D,A)=H(D)-H(D|A)$

3.5 信息增益比

以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题，使用信息增益比可以对这一问题进行校正。
【信息增益比】特征 A 对训练数据集 D 的信息增益比 $g_R(D,A)$ 定义为其信息增益 $g(D,A)$ 与训练数据集 D 关于特征 A 的值的熵 $H_A(D)$ 之比，即
$g_A(D,A)=\frac{g(D,A)}{H_A(D)}$,
其中 $H_A(D)=-\begin{array}{c}{\sum }_{i=1}^n\frac{|D_i}{|D|}lo{g}_2\frac{|D_i}{|D|}\end{array}$, n是特征值 A 的取值个数。

3.6 基尼指数

• 分类问题中，假设有 K 个类，样本点属于第 k 类的概率为 $p_k$, 则概率分布的基尼指数定义为：
  $Gini(p)=\begin{array}{c}{\sum }_{k=1}^K{p}_k(1-p_k)\end{array}=1-\begin{array}{c}{\sum }_{k=1}^K{p}_k^2\end{array}$

• 给定样本结合D，其基尼指数为
  $Gini(D)=1-\begin{array}{c}su{m}_{k=1}^K(\frac{|C_k|}{|D|}{)}^2\end{array}$
  其中，$C_k$ 是 D 中属于第 k 类的样本子集， K 是类的个数。

• 如果样本集合 D 根据特征 A 是否取某一可能值 a 被分割为 $D_1$ 和 $D_2$, 则在特征 A 的条件下，集合 D 的基尼指数定义为:
  $Gini(D,A)=\frac{|D_1}{|D|}Gini(D_1)+\frac{|D_2}{|D|}Gini(D_2)$

• 基尼指数值越大，样本集合的不确定性也就越大。

4. 算法

4.1 ID3 算法

• ID3 算法的核心是在决策树各个节点上应用信息增益准则选择特征，递归地构建决策树。
• 具体方法是：从根结点开始，对结点计算所有可能的特征的信息增益，选择信息增益最大的特征作为结点的特征，由该特征的不同取值建立子结点；再对子结点递归地调用以上的方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止。
• ID3 算法生成的树容易产生过拟合。

4.2 C4.5的生成算法

C4.5 的生成算法与 ID3 算法类似， C4.5 算法对 ID3 算法进行了改进， C4.5 在生成树的过程中，用信息增益比来选择特征。

4.3 CART 算法

CART 又称分类回归树，CART 算法与 C4.5 算法类似，CART 在生成树的过程中，用基尼指数来选择特征

参考：

• 李航.《统计学习方法》第一版
• 极客时间.陈旸.数据分析实战45讲
• https://www.zybuluo.com/rianusr/note/1160843

最后

以上就是饱满吐司为你收集整理的决策树理论1. 决策树模型（以分类树为例）2. 决策树学习3. 特征选择的标准4. 算法的全部内容，希望文章能够帮你解决决策树理论1. 决策树模型（以分类树为例）2. 决策树学习3. 特征选择的标准4. 算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。