决策树--学习笔记（一）

• 信息熵

• 决策树

• 决策树优化

• 剪枝

• 决策树可视化

                                              决策树的直观理解

比特化（bits）

假设存在一组随机变量x，各个值出现的概率关系如图：

现在有一组由x变量组成的序列：BACADDCBAC......;如果现在希望这个序列转换为二进制来进行网络传输，那么我们就得到一个这样的序列：

01001000111110010010......

结论：在这情况下，我们可以使用两个比特位来表示一个随机变量。

而当x变量出现的概率值不一样的时候，对于一组序列信息来讲，每个变量的平均值需要多少比特位来描述呢？

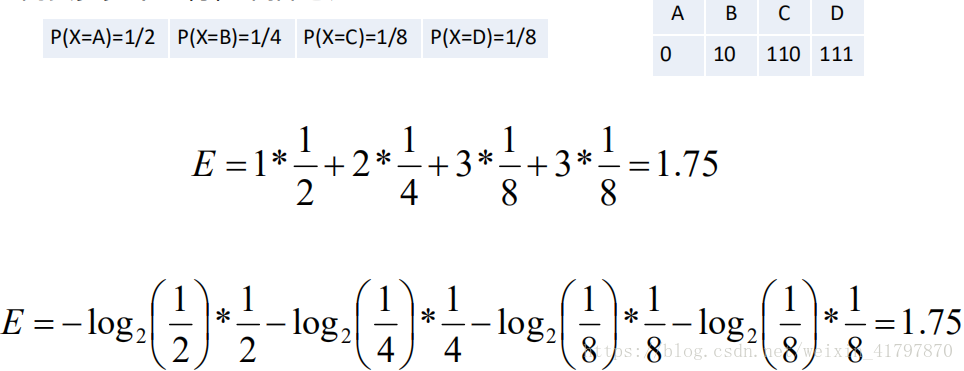
一般化的比特化（Bits）

假设现在随机变量X具有m个值，分别为V1，v2,...vm；并且各个值出现的概率如下表所示：那么对于一组列信息来讲，每个变量平均需要多少个比特位来描述呢？

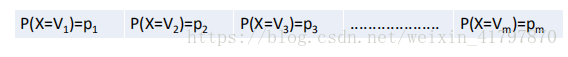
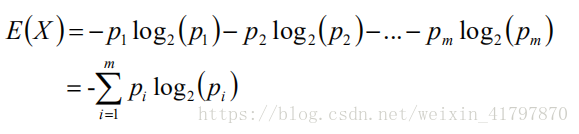
信息熵（Entropy）

H(X)就叫做随机变量X的信息熵：

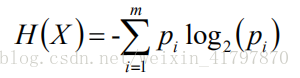
信息量：指的是一个样本/事件所蕴含的信息，如果一个事件的概率越大，那么就可以认为该事件所蕴含的信息越少。

信息熵就是用来描述系统信息量的不确定度。

高信息熵：表示随机变量X均匀分布的，各个取值情况是等概论出现的。

低信息熵：表示随机变量X各种取值不是等概率出现的。可能概率很大，也可能很小。

条件熵H(Y|X)

给定条件X 的情况下，随机变量Y的信息熵就就叫做条件熵。

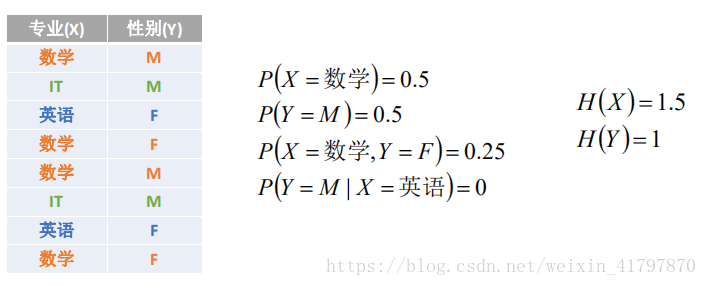
当专业为数学时，Y的信息熵的值为：H(Y|X=数学)

H(Y|X=数学)=-1/2log2(1/2)-1/2log2(1/2)=1

给定条件X的情况下，所有不同情况下Y的信息熵法的平均值叫做条件熵。

给定条件X的情况下，所有不同X值情况下Y的信息熵的平均值叫做条件熵。另外一个公式如下所示：

H(Y|X)=H(X,y)-H(X)

事件（X,Y）发生所包含的熵，减去事件X单独发生的熵，即为在事件X发生的前提下，Y发生“新”带来的熵，这个就是条件熵本身的概念。

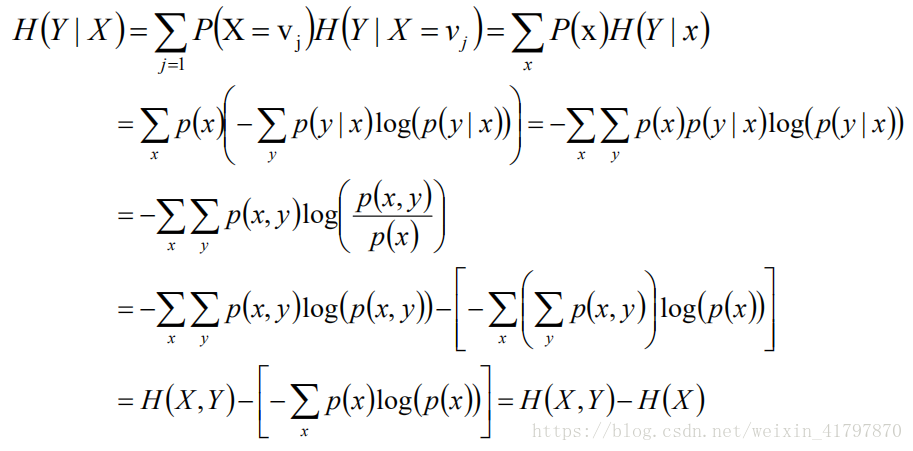
决策树

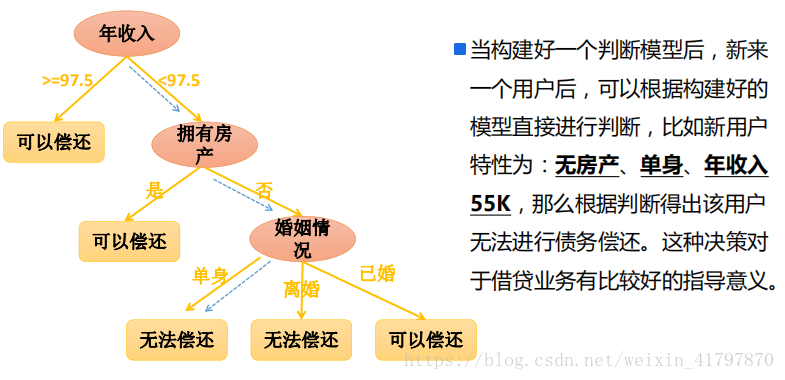
决策树（Decision Tree）是在已知各种情况下发生概率的基础上，通过构建决策树来进行分析的一种方式，是一种直观应用概率分析的一种图解法；决策树是一种预测模型，代表的是对象属性与对象值之间的映射关系；决策树是一种树形结构，其中每个内部节点表示一个树形的测试，每个分支表示一个测试输出，每个叶子节点代表一种类别；决策树是一种非常常用的有监督的分类算法。

决策树的决策过程就是从根节点开始，测试待分类项中对应的特征属性，并按照其值选择输出分支，知道叶子节点，将叶子节点的存放类别作为决策结果。

决策树分为两大类：分类树和回归树，前者用于分类标签值，后者用于预测连续值，常用算法ID3、C4.5、CART等。

决策树构建过程

决策树构建的重点就是决策树的构造。决策树的构造就是进行属性选择度量，确定各个特征属性之间的拓扑结构（树结构），构建决策树的关键就是分裂属性，构建决策树的关键步骤就是分裂属性，分裂属性是指在某个节点按照某一特征属性的不同划分构建不同的分支，其目标就是让哥哥分裂子集尽可能的“纯”（让一个分裂子类的项尽可能的属于同一类别）

根据特征属性的类型不同，在构建决策树的时候，采用不同的方式，具体如下：
属性是离散值，而且不要求生成的是二叉决策树，此时一个属性就是一个分支
属性是离散值，而而且要求生成的是二叉决策树，此时使用属性划分的子集进行测试，按照
“属于此子集”和“不属于此子集”分成两个分支
属性是连续值，可以确定一个值作为分裂点split_point，按照>split_point和
<=split_point生成两个分支

最后

以上就是舒适奇迹为你收集整理的决策树--学习笔记（一）的全部内容，希望文章能够帮你解决决策树--学习笔记（一）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。