来源 | AI小白入门
作者 | 文杰
编辑 | yuquanle
完整代码见：原文链接

本文介绍了ID3，C4.5，CART三种基本的决策树模型。首先介绍了决策树的特征选择，包括信息增益，信息增益率、基尼指数、最小均方差分别对应分类树ID3、C4.5、CART、回归树CART。然后介绍了决策树建树的一般流程、对比分类树和回归树建树的区别。最后介绍了树模型中避免过拟合问题的剪枝方法，包括前剪枝和后剪枝。

决策树简介

决策树是一种基本的分类和回归方法，用于分类主要是借助每一个叶子节点对应一种属性判定，通过不断的判定导出最终的决策；用于回归则是用均值函数进行多次二分，用子树中数据的均值进行回归。

决策树算法中，主要的步骤有：特征选择，建树，剪枝。接下来将介绍三种典型的决策树算法：ID3，C4.5，CART。

优点：

• 可解释性好，易可视化 ，特征工程中可用特征选择。

• 样本复杂度$O(log(n))$，维度灾难。

缺点：

• 易过拟合，学习最优模型N-P难，贪心搜索局部最优。

• 虽然是非线性模型，但不支持异或逻辑。

• 数据不均衡时不适合决策树。

• 决策属性不可逆。

特征选择

对于决策树而言，每一个非叶子节点都是在进行一次属性的分裂，选择最佳的属性，把不同属性值的样本划分到不同的子树中，不断循环直到叶子节点。其中，如何选择最佳的属性是建树的关键，决策树的一个特征选择的指导思想是熵减思想。

常见的选择方式有ID3的信息增益，C4.5的信息增益率，CART的基尼指数，最小均方差。这里分别介绍这ID3，C4.5，CART决策树的特征选择标准

信息增益

为了更清楚的理解信息增益这个概念，我们需要先来了解下信息论中的信息熵，以及条件熵的概念。

熵是一种对随机变量不确定性的度量，不确定性越大，熵越大。

假设离散随机变量$Y$的概率分布为$P(Y)$，则其熵为：
$$\begin{gathered} H(Y)=-\sum _{y}P(y)logP(y) \\ =-\sum _{k=1}^K\frac{|C_k|}{|D|}log\frac{|C_k|}{|D|} \end{gathered}$$
其中熵满足不等式$0\le H(Y)\le log|Y|$。

在进行特征选择时尽可能的选择在属性$X$确定的条件下，使得分裂后的子集的不确定性越小越好（各个子集的信息熵和最小），即$P(Y|X)$的条件熵最小。
$$\begin{gathered} H(Y|X)=-\sum _{x,y}P(x,y)log(P(y|x)) \\ =-\sum _{x_i\in X}\sum _{x_i,y}P(y,x_i)logP(y|x_i) \\ =-\sum _{i=1}^n\frac{|X_i|}{|X|}H(X_i) \end{gathered}$$
其中$X_i$是表示属性$X$取值为$i$构成的子集。

信息增益表示的就是在特征$X$已知的条件下使得类别$Y$的不确定性减少的程度。即为特征$X$对训练数据集$D$的信息增益为：
$$Gain(Y,X)=H(Y)-H(Y|X)$$
用信息增益来进行特征选择，的确可以选择出那些对于类别敏感的特征。

值得注意的是，信息增益没有考虑属性取值的个数的问题。因为划分的越细，不确定性会大概率越小，因此信息增益倾向于选择取值较多的特征。

如对于数据表中主键这样的属性，用信息增益进行属性选择，那么必然会导致信息增益率最大，因为主键与样本是一一对应关系，而这样做分类是无意义的，即信息增益不考虑分裂后子集的数目问题。

信息增益比

信息增益偏向于选择特征值取值较多的特征，而信息增益比通过将训练集关于特征$X$的信息熵作为分母来限制这种倾向。

信息增益比定义为信息增益比上特征$X$的信息熵：
$$Gai{n}_{ratio}=\frac{Gain(Y,X)}{H(X)}$$
其中$H(X)=-{\sum }_{x}P(x)logP(x)$。

基尼指数

基尼指数特征选择准则是CART分类树用于连续值特征选择，其在进行特征选择的同时会决定该特征的最优二分阈值。基尼指数是直接定义在概率上的不确定性度量：
$$\begin{gathered} Gini(D)=1-\sum _{k=1}^K{p}_k^2 \\ =1-\sum _{i=1}^K{\left(\frac{|C_k|}{|D|}\right)}^2 \end{gathered}$$
可以看出，基尼指数与信息熵的定义极为一致。

最小均方差

最小均方差应用于回归树，回归问题一般采用最小均方差作为损失。在特征选择的同时会测试不同的二分阈值的最小均方误差，选择最有的特征和阈值：
$$\underset{j,s}{\min }\left[\underset{c_1}{\min }\sum _{x_i\in R_1(j,s)}(y_i-c_1{)}^2+\underset{c_2}{\min }\sum _{x_i\in R_2(j,s)}(y_i-c_2{)}^2\right]$$
其中$c_i$是第$i$个模型的回归值。

特征选择准则对比：

• ID3采用信息增益，C4.5采用信息增益率，CART分类采用基尼指数，CART回归采用最小均方误差；

• 信息增益，信息增益率，基尼指数都是用于分类树，最小均方误差用于回归树；

• 信息增益，信息增益率同样可以处理连续值得情况，一般来讲连续值的处理只作二分，所以CART回归是一个标准的二叉树形式。

建树

ID3和C4.5，CART分类树

• 输入：训练集$D$，特征集$A$，阈值$ϵ$

• 输出：决策树$T$

1. 若$D$中所有样本属于同一类$C_k$，$T$为叶子节点，并将该叶子节点的类别标记为$C_k$，返回上一次递归。

2. 若$A=\varnothing$，即所有的属性都使用完了，$T$为叶子节点，并把该子集中最多一类$C_k$标记为该叶子节点的类别，返回上一次递归。否则，3）

3. 进行特征选择。选择信息增益(信息增益比,基尼指数)最大的特征$A_g$，如果$A_g$的信息增益（信息增益率,基尼指数）小于预设的阈值$ϵ$，同样$T$为叶子节点，并把该子集中最多一类$C_k$标记为该叶子节点的类别，返回上一次递归。否则，4）

4. 符合建树要求。对$A_g$的每一个可能值$a_i$，依次$A_g=a_i$将$D$分割为若干个非空子集$D_i$，将$D_i$中实例最多的类别标记为该节点的类别$C_k$，依次以$D_i$为样本集，$A-A_g$为特征集，递归的调用（1-4）步，直到结束。

CART回归树

由于回归树不存在剩余样本属于一类或者特征用完的情况，所以分类树没有前面的前面两步。

1. 对每一个特征进行步长（样本）循环搜索不同阈值下的最小的均方误差记为该特征的均方误差，从所有特征的均方误差选择出最小均方误差。如果最小均方误差小于预设的最小误差，或者分裂后的子集的样本数小于预设的最小值，则进行建立叶子节点$T$，返回上一次递归。

2. 否则，以特征$A_g$作为分裂属性，根据阈值$\varphi$进行二分，建立左右子树，建立线性回归模型。递归（1-2）步，直到结束。

分类树和回归树建树区别：

• 回归树中特征可以重复进行选择，而分类树的特征选择只能用一次。

• 回归树比分类树少了特征集合为空，样本集合同属一类这两个返回标志，只能人工干预（指标无提升）。

• 对于特征下划分阈值的分裂，一般只作二分裂，不然就成了密度估计问题了。

剪枝

决策树生成算法递归生成的决策树，按照建树的过程直到结束。这样产生的决策树往往对训练集的分类很准确，但是对未知数据却没有那么准确，容易出现过拟合现象。因此，决策树需要借助验证集来进行剪枝处理，防止决策树过拟合。

预剪枝

预剪枝是在构造决策树的过程中，对比属性划分前后决策树在验证集上是否由精度上的提高。由于非叶子节点中的样本往往不属于同一类，采用多数样本标记为该节点的类别进行决策。若划分后的决策树在精度上有提高，则正常分裂，否则进行剪枝。其过程是一个贪心过程，即每一次划分都必须使得决策精度有所提高。

当然也可以对建树进行约束，比如信息增益小于一定阈值的情况或者建树之后其中一个子集的样本数小于一定数量进行预剪枝，统计学习方法书中采用熵加叶子节点树作为损失函数来控制预剪枝。

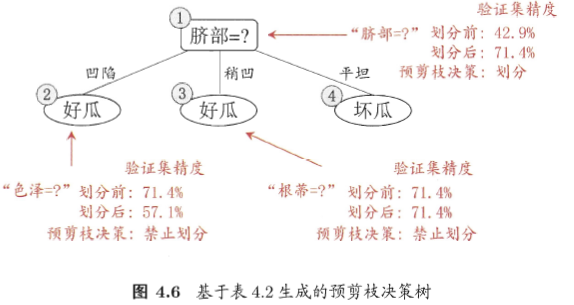
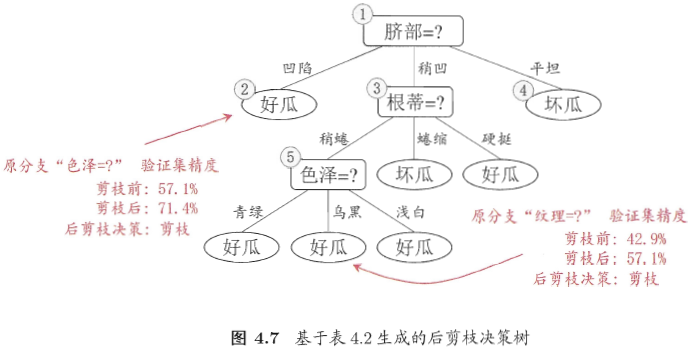
后剪枝

后剪枝是在决策树建立后以后，自底向上的对决策树在验证集上对每一个非叶子节点判断剪枝前和剪枝后的验证精度，若剪枝后对验证精度有所提高，则进行剪枝。

不同于预剪枝的是，预剪枝是对划分前后的精度进行比较，而后剪枝是对剪枝前和剪枝后的验证精度进行比较，相对于预剪枝，后剪枝决策树的欠拟合风险小，泛化能力优于预剪枝，但时间开销大。

决策树总结

• ID3,C4.5,CART没有必要严格按照特征选择方式，建树过程严格划分。

• 决策树选择从问题出发，如果是回归问题，可以采用CART回归树，如果是分类问题那么采用分类树。

• 决策树选择从数据出发，如果属性是连续值，二分离散化建二叉树，如果属性是离散值，则建多叉树。

• 特征选择准则可以互用，一般来讲连续值得特征可以反复选择，而离散值的特征只能用一次。

代码实战

double calcShannonEntOrGini(const DataStr &data, const string &type) 
{ 
 unsigned int i; 
 map<string,double> label_value;//每一类样本的个数统计 
 double prob=0; 
 double shannoEnt=0; 
 double Gini=1; 
 string label; 
 for(i=0; i<data.size(); i++) 
 { 
 label=data[i][data[0].size()-1]; 
 if(label_value.count(label)) 
 label_value[label]+=1;//如果类别已初始化则在之前的基础上加1 
 else 
 label_value[label]=1;//如果类别未初始化，则把当前类别下样本数初始化为1 
 } 
 //统计该子数据集上的所有样本的决策属性以及不同决策属性上样本数 
 for(map<string,double>::iterator it=label_value.begin();it!=label_value.end();it++) 
 { 
 prob=it->second/data.size(); 
 shannoEnt-=prob*log(prob); 
 Gini-=prob*prob; 
 } 
 //cout<<"shannoEnt="<<shannoEnt<<endl; //检测信息熵计算是否正确 
 if(type=="Gini") 
 return Gini; 
 if(type=="Ent") 
 return shannoEnt; 
 return shannoEnt; 
 }

更多AI、NLP干货资源请关注公众号：AI小白入门（ID: StudyForAI）

最后

以上就是缓慢星月为你收集整理的【机器学习】决策树决策树简介特征选择建树剪枝代码实战的全部内容，希望文章能够帮你解决【机器学习】决策树决策树简介特征选择建树剪枝代码实战所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。