一文了解决策树

决策树

决策树是一种非参数监督学习算法，用于分类和回归任务。它具有分层的树结构，由根节点、分支、内部节点和叶节点组成。

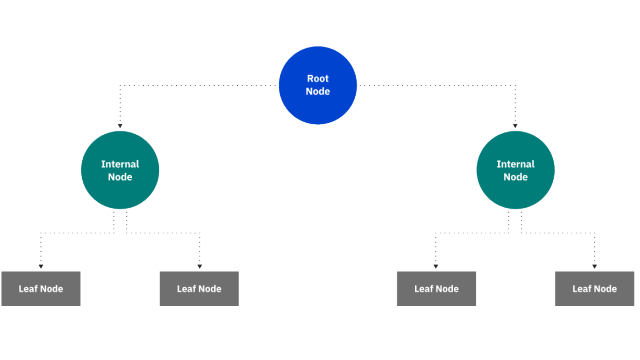
从上图中可以看出，决策树从一个根节点开始，它没有任何传入的分支。然后从根节点传出的分支馈送到内部节点，也称为决策节点。根据可用特征，两种节点类型都进行评估以形成同质子集，这些子集由叶节点或终端节点表示。叶节点代表数据集中所有可能的结果。例如，假设您正在尝试评估是否应该去冲浪，您可以使用以下决策规则来做出选择：

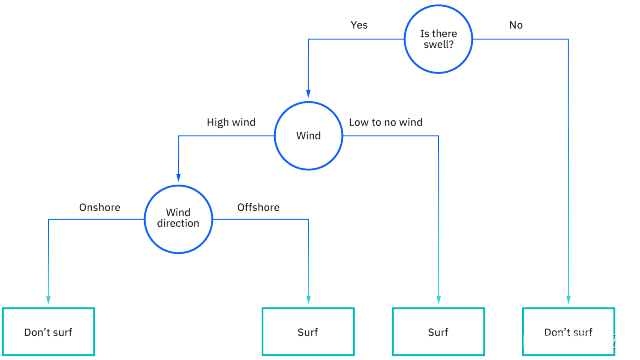
这种类型的流程图结构还创建了一个易于理解的决策表示，允许组织中的不同组更好地理解为什么做出决策。

决策树学习采用分而治之的策略，通过贪婪搜索来识别树中的最佳分割点。然后以自上而下的递归方式重复此拆分过程，直到所有或大多数记录都已分类到特定的类别标签下。是否所有数据点都被归类为同质集很大程度上取决于决策树的复杂性。较小的树更容易获得纯叶节点——即单个类中的数据点。然而，随着树的大小越来越大，保持这种纯度变得越来越困难，并且通常会导致给定子树中的数据太少。发生这种情况时，称为数据碎片，通常会导致过度拟合. 因此，决策树偏爱小树，这与奥卡姆剃刀中的简约原则是一致的；也就是说，“实体不应过度增加”。换句话说，决策树仅在必要时才应增加复杂性，因为最简单的解释通常是最好的。为了降低复杂度和防止过拟合，通常采用剪枝；这是一个过程，它删除了在重要性较低的特征上分裂的分支。然后可以通过交叉验证过程评估模型的拟合度。决策树可以保持其准确性的另一种方法是通过随机森林算法形成一个集成；这个分类器可以预测更准确的结果，特别是当单个树彼此不相关时。

决策树的类型

Hunt 的算法是在 1960 年代开发的，用于模拟心理学中的人类学习，它构成了许多流行的决策树算法的基础，例如：

- ID3： Ross Quinlan 参与了 ID3 的开发，ID3 是“Iterative Dichotomiser 3”的简写。该算法利用熵和信息增益作为评估候选分裂的指标。可以在 此处找到 Quinlan 从 1986 年开始对该算法的一些研究 （PDF，1.3 MB）（链接位于 ibm.com 之外）。

- C4.5： 该算法被认为是 ID3 的后期迭代，也是由 Quinlan 开发的。它可以使用信息增益或增益比来评估决策树中的分割点。

- CART： 术语 CART 是“分类和回归树”的缩写，由 Leo Breiman 引入。该算法通常利用 Gini 杂质来识别要拆分的理想属性。基尼杂质测量随机选择的属性被错误分类的频率。使用 Gini 杂质进行评估时，较低的值更理想。

如何在每个节点选择最佳属性

虽然有多种方法可以在每个节点处选择最佳属性，但有两种方法，信息增益和 Gini 杂质，作为决策树模型的流行分裂标准。它们有助于评估每个测试条件的质量以及它将样本分类到一个类别的能力。

熵和信息增益

如果不首先讨论熵，就很难解释信息增益。熵是一个源于信息论的概念，它衡量样本值的杂质。它由以下公式定义，其中：

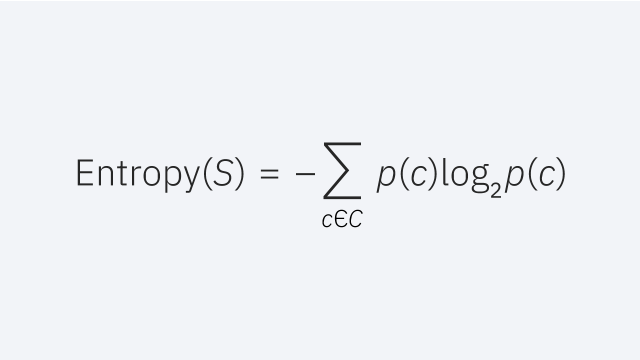
熵公式

• S代表熵计算的数据集
• c 表示集合中的类，S
• p( c )表示属于c类的数据点占集合中总数据点数的比例，S

熵值可以介于 0 和 1 之间。如果数据集 S 中的所有样本都属于一个类，则熵将等于 0。如果一半样本归为一类，另一半属于另一类，则熵最高为 1。为了选择最佳特征进行分割并找到最优决策树，具有最小的属性应该使用熵。信息增益表示给定属性拆分前后熵的差异。具有最高信息增益的属性将产生最佳拆分，因为它在根据其目标分类对训练数据进行分类方面做得最好。信息增益通常用以下公式表示，其中：

信息增益公式

• a表示特定的属性或类标签
• Entropy(S) 是数据集的熵，S
• |Sv|/ |S| 表示 S v中的值占数据集中值个数的比例，S
• Entropy(S v ) 是数据集的熵，S v

让我们通过一个例子来巩固这些概念。假设我们有以下任意数据集：

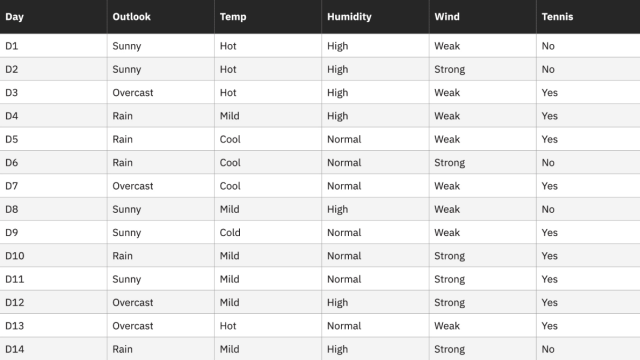
对于这个数据集，熵是 0.94。这可以通过找到“打网球”为“是”的天数比例为 9/14 和“打网球”为“否”的天数比例为 5/14 来计算。然后，这些值可以代入上面的熵公式。

Entropy (Tennis) = -(9/14) log2(9/14) – (5/14) log2 (5/14) = 0.94

然后我们可以单独计算每个属性的信息增益。例如，属性“湿度”的信息增益如下：

Gain (Tennis, Humidity) = (0.94)-(7/14)*(0.985) – (7/14)*(0.592) = 0.151

作为回顾，

- 7/14 表示Humidity等于“high”的值与Humidity值总数的比例。在这种情况下，Humidity等于“high”的值的数量与Humidity等于“normal””的值的数量相同。

- 0.985 是当 Humidity = “high” 时的熵

- 0.59 是当 Humidity = “normal” 时的熵

然后，对上表中的每个属性重复计算信息增益，选择信息增益最高的属性作为决策树中的第一个分裂点。在这种情况下，outlook 会产生最高的信息增益。从那里，对每个子树重复该过程。

基尼系数

基尼系数是根据数据集的类分布对数据集中的随机数据点进行错误分类的概率。与熵类似，如果集合 S 是纯的（即属于一个类），那么它的不纯性为零。这由以下公式表示：

基尼系数公式

决策树的优缺点

虽然决策树可用于各种用例，但其他算法通常优于决策树算法。也就是说，决策树对于 数据挖掘 和知识发现任务特别有用。让我们在下面进一步探讨使用决策树的主要好处和挑战：

好处

- 易于解释： 决策树的布尔逻辑和可视化表示使它们更易于理解和使用。决策树的分层特性还可以很容易地看出哪些属性是最重要的，而其他算法（如 神经网络）并不总是清楚这一点。

- 几乎不需要数据准备： 决策树具有许多特征，使其比其他分类器更灵活。它可以处理各种数据类型——即离散值或连续值，并且可以通过使用阈值将连续值转换为分类值。此外，它还可以处理具有缺失值的值，这对于其他分类器（例如朴素贝叶斯）来说可能是有问题的。

- 更灵活： 决策树可用于分类和回归任务，使其比其他一些算法更灵活。它对属性之间的潜在关系也不敏感；这意味着如果两个变量高度相关，算法将只选择其中一个特征进行分割。

缺点

- 容易过度拟合： 复杂的决策树往往会过度拟合并且不能很好地推广到新数据。这种情况可以通过预剪枝或后剪枝的过程来避免。预剪枝在数据不足时停止树的生长，而后剪枝在树构建后删除数据不足的子树。

- 高方差估计器： 数据中的微小变化可以产生非常不同的决策树。Bagging或估计的平均，可以是减少决策树方差的一种方法。然而，这种方法是有限的，因为它可能导致高度相关的预测因子。

- 成本更高： 鉴于决策树在构建过程中采用贪婪搜索方法，与其他算法相比，它们的训练成本可能更高。

- scikit-learn 不完全支持： Scikit-learn 是一个流行的基于 Python 的机器学习库。虽然这个库确实有一个 决策树模块（DecisionTreeClassifier，链接位于 ibm.com 之外），但当前的实现不支持分类变量。

原文地址：
https://www.ibm.com/topics/decision-trees

最后

以上就是无辜月光为你收集整理的一文了解决策树的全部内容，希望文章能够帮你解决一文了解决策树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。