概述
第九讲：Decision Tree
1、Decision Tree Hypothesis
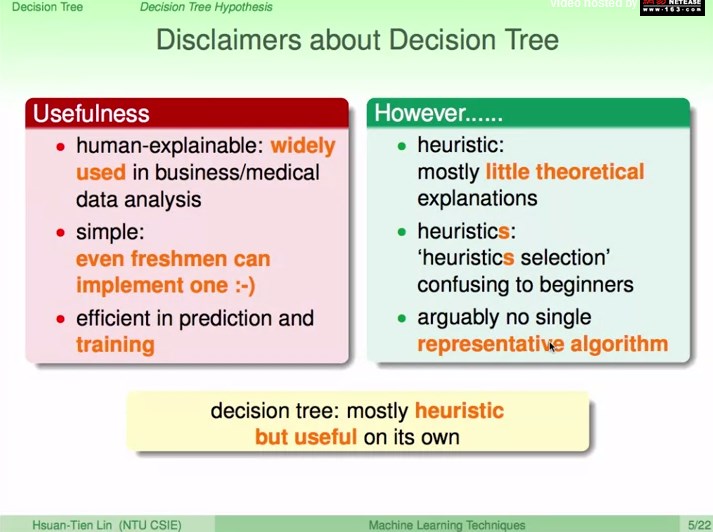
复习：aggregation model
把g融合成效果好的G，有两种面向：
1、blending：已有g。（
平均、线性、非线性
）
2、learning：开始没有g，一边学习g一边融合起来。（
boostrap产生多副本、差异性大的g、不同条件使用不同的g
）
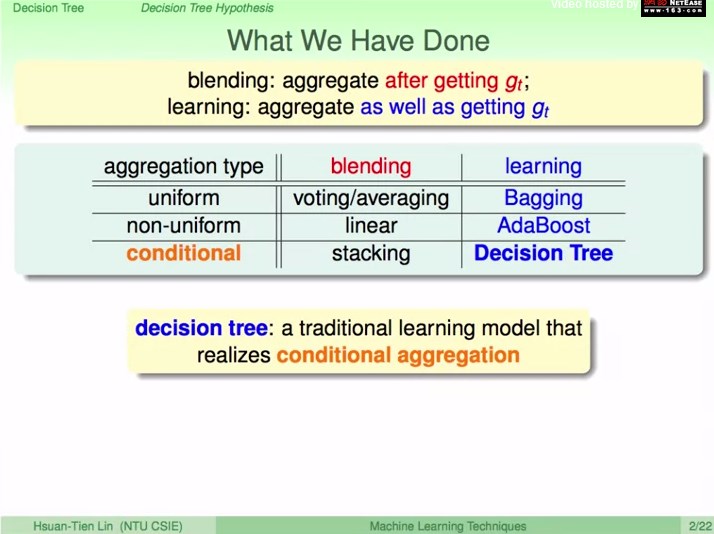
决策树的融合角度：
不同条件使用不同的g
g：简单判别，叶节点
q：条件，路径
决策树：模仿人类的决策过程
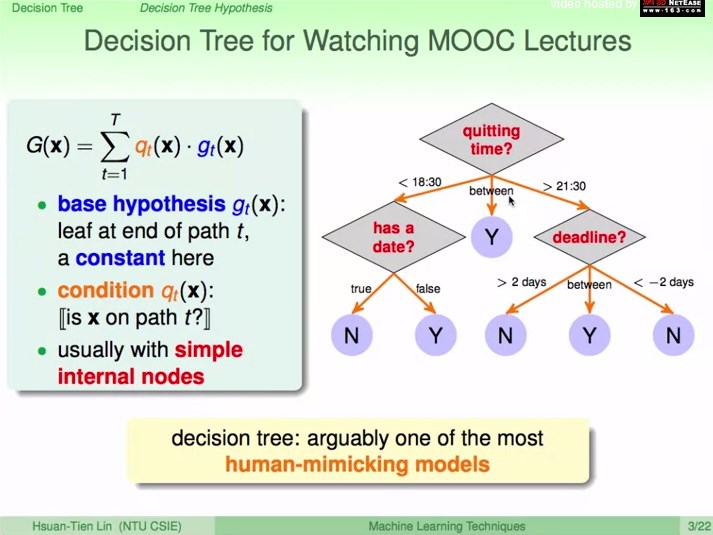
决策树的递归角度：
根据条件分支到子树
G：整棵树
b：分支条件
Gc：c分支的子树
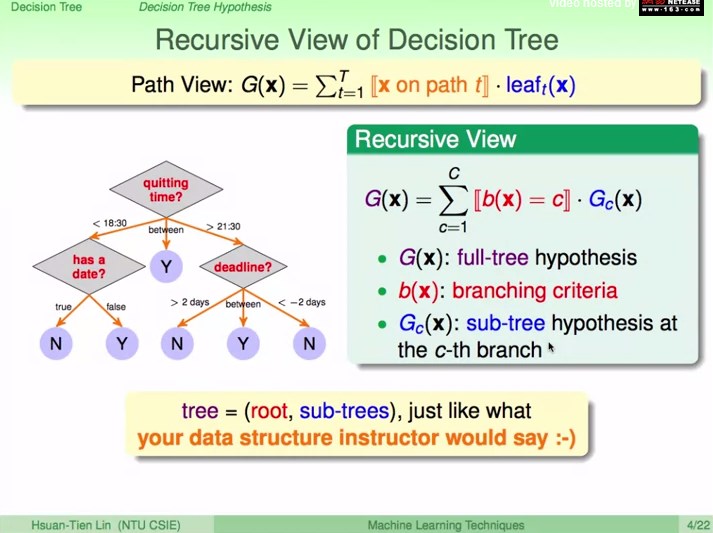
决策树状况
有点：
人类决策过程的解释性、
简单、训练和预测过程高效
缺点：缺少理论保证、需要探索、没有代表性的决策树算法
总结：前人探索性的思考，没理论上的保证，但使用起来效果不错
2、Decision Tree Algorithm
基本的决策树算法：
递归方式表达
四个需要决定的地方：
1、分支个数C
2、分支决策b
3、停止条件
4、回传g
CART算法（Classification and Regression Tree）
1、分支个数C=2（二叉树）
4、回传g=使得E
in最好的常数（分类：较多的类。回归：平均数）
CART算法（Classification and Regression Tree）
2、分支决策b：
使用decision stump一分为二，使得分开后的dataset更“纯”（相等或接近）
计算公式：
所有
decision stump，切开后看两边数据D1和D2纯或是不纯，根据数据集大小
加权，
最小化得到最纯的
decision stump。
不纯度函数
分类常用Gini（考虑
所有类别
），回归常用Regression Error（Ein）
CART算法（Classification and Regression Tree）
3、停止条件：
被迫停止（y都相同或x都相同）：完全生长树
3、Decision Tree Heuristic in CART
复习CART算法：
二分，纯化数据来做分支，直到不能再分则停止，回传对E
in
最好的常数
正规化：剪枝
完全生长树会导致过拟合
一个衡量棵树复杂程度的方法：叶子节点的数量
剪枝决策树：E
in和复杂度加权
类别特征的分支
数值特征：decision stump
类别特征：decision subset
缺省特征：找替代品
寻找替代特征，要求和缺省特征在分支上的表现最接近
4、Decision Tree in Action
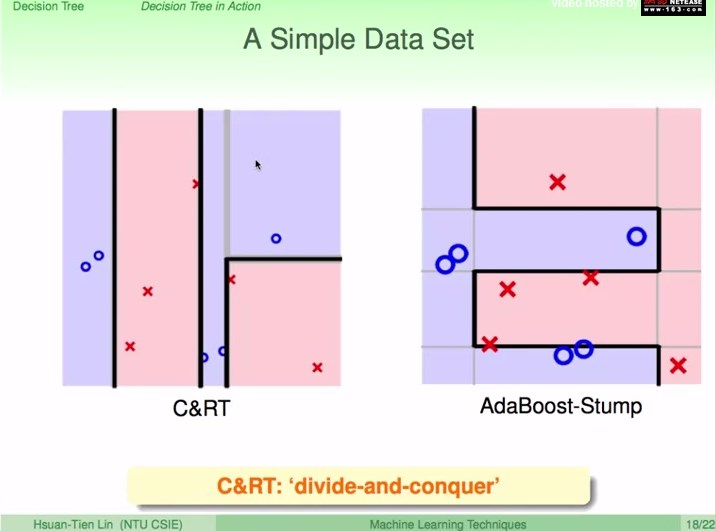
CART和AdaBoost-Stump
CART：条件切分
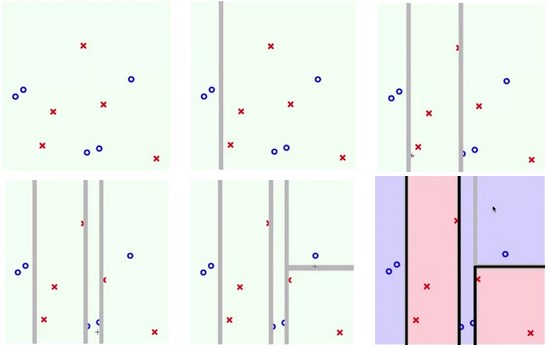
AdaBoost-Stump：更关注上一轮切分错的点
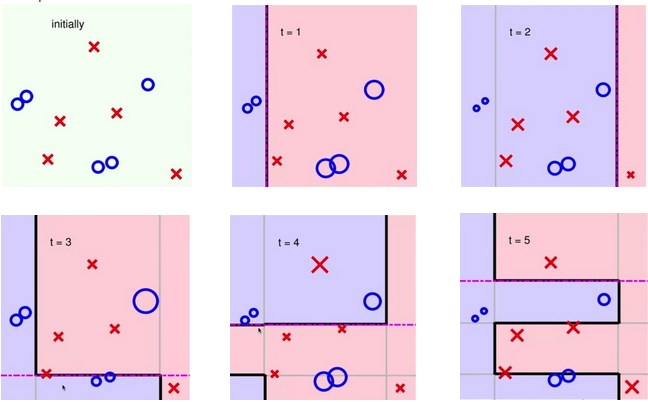
AdaBoost-Stump横跨整个平面
切分
decision tree在条件之下切分
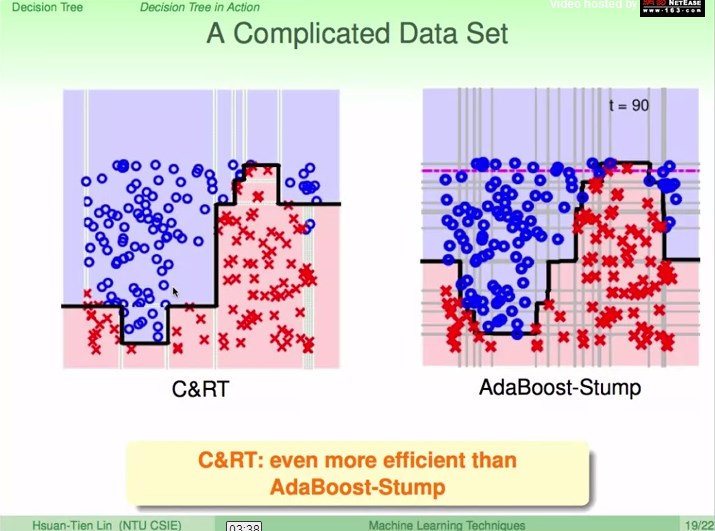
复杂dataset的表现
CART的条件切割比较细致，比AdaBoost-Stump更高效
CART的实物表现：
1、类似于人的决策方式
2、可处理多类别
3、课处理类别特征
4、可处理缺省特征
5、很有效的得到非线性模型
最后
以上就是昏睡白开水为你收集整理的《机器学习技法》第九讲：Decision Tree 第九讲：Decision Tree的全部内容，希望文章能够帮你解决《机器学习技法》第九讲：Decision Tree 第九讲：Decision Tree所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![[Mitchell 机器学习读书笔记]——决策树学习](/uploads/reation/bcimg3.png)
发表评论 取消回复