写在前面
正所谓“三个臭皮匠,顶个诸葛亮”,在机器学习中也存在这样的哲理。提升方法(Boosting)就是这样的代表:通过将一系列弱学习器综合提升为强学习器的算法。Boosting族算法的工作机制:(1)先从初试训练集训练出一个基学习器;(2)再根据基学习器的表现对训练样本进行调整,使得先前基学习器做错的训练样本在后续训练中受到更多关注;(3)基于调整后的训练样本继续训练下一个基学习器;(4)如此重复进行,直至基学习器数目达到事先设定的值T,最终将这T个基学习器进行加权结合。(啊哈就是这样的过程,具体的实例可以参考林轩田老师机器学习技法的课件Lecture8)
在Boosting family中,最具代表性的实现就是Adaboost。
1.AdaBoost简介
AdaBoost是英文"Adaptive Boosting"(自适应增强)的缩写,它的自适应在于:前一个基本分类器被错误分类的样本的权值会增大,而正确分类的样本的权值会减小,并再次用来训练下一个基本分类器。同时,在每一轮迭代中,加入一个新的弱分类器,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数才确定最终的强分类器。
2.AdaBoos算法
输入: 训练数据集T(二分类问题);弱学习算法;
输出:最终分类器G(x)
(1)初始化训练数据的权值分布。第一步假设具有相同的权值分布,即:
(2)反复学习基本分类器,在每一轮m=1,2,...,M,循环执行:
(a)使用当前分布Dm加权的训练数据集,学习基本分类器Gm(x);
(b)计算基本分类器Gm(x)在加权训练数据集上的分类误差率:
(c)计算基本分类器Gm(x)的系数:
ps.这里log应为ln,自然对数
这里alpha表示重要性,有数学定义可知,alpha随着e的减小而增大,说明分类误差率越小的分类器在最终分类器中的权重越大。
(d)更新训练数据集的权值分布
其中,Zm是规范化因子:
上式更新权重Wm+1还可以写成以下形式:
由此可知,被误判的样本权值在下一轮训练中得以增大,而正确分类的权重减小。
(3)构建基本分类器的线性组合
以此得到最终的分类器
3.AdaBoost算法解释
AdaBoost可以理解为模型为加法模型、损失函数为指数函数、学习算法为前向分步算法的二类分类学习方法。
前向分布算法
前向分步算法总体思路:学习的是加法模型,从前往后,每一步只学习一个基函数及其系数,逐步逼近优化目标函数式。
这样就把同时求解从m=1到M的所有参数问题简化为逐次求解每哥循环的参数问题。
算法具体步骤实现:

再次观察AdaBoost分类器形式可以发现,它就是前向分步算法的一个特例。
4.AdaBoost实例
扯了这么多,数学的东西毕竟还是比较抽象,这里给出一个利用AdaBoost算法实现二分类的实例。
Adaboost算法原理分析和实例+代码(简明易懂)
这里大神用的是matlab实现代码,晚上打算看看自己能不能参考着写一个python版本的~
5.小结
AdaBoost是Boosting方法中最流行的一种算法。它是以弱分类器作为基础分类器,输入数据之后,通过加权向量进行加权,;在每一轮的迭代过程中都会基于弱分类器的加权错误率,更新权重向量,从而进行下一次迭代。并且会在每一轮迭代中计算出该弱分类器的系数,该系数的大小将决定该弱分类器在最终预测分类中的重要程度。显然,这两点的结合是adaBoost算法的优势所在。
优点:泛化错误率低,容易实现,可以应用在大部分分类器上,无参数调整
缺点:对离散数据点敏感
最后在网上找了一张AdaBoost的框架图,加深印象~
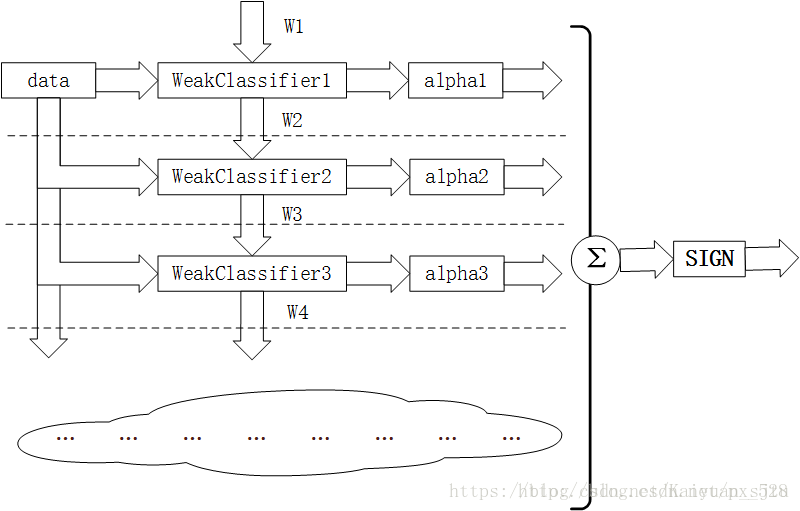
以上~
2018.04.18
最后
以上就是眼睛大彩虹最近收集整理的关于机器学习算法总结之Boosting:AdaBoost的全部内容,更多相关机器学习算法总结之Boosting内容请搜索靠谱客的其他文章。








发表评论 取消回复