一)进制简介
十进制是人与人之间一种通用计算方式。
二进制是计算机中一种通用计算方式。
为了方便两者之间计算,所以需要进行进制转换。
由于十进制存在整数和小数的情况,在转二进制时,一般是先计算整数部分,再计算小数部分,再加以合并。
二)十进制转二进制
整数位转换原理:十进制转二进制采用“除2取余,逆序排列”法。
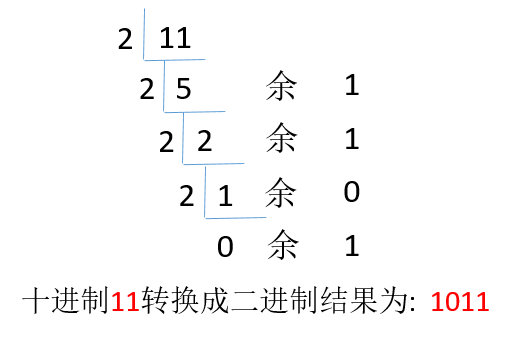
例如:把十进制11转二进制步骤如下:
第一步:11除以2=5 余1
第二步:5除以2=2 余1
第三步:2除以2=1 余0
第四步:1除以2=0 余1
结论:把余数逆序排列,11的二进制为1011。
图解:
小数位转换原理:十进制转二进制采用"乘2取整,顺序排列"法。
例如:把十进制11.25转二进制步骤如下:
先计算整数部分,11的二进制为1011
再计算小数部分0.25
第一步:0.25 * 2 = 0.5,取整数位0,结果为0.0
第二步:0.5 * 2 = 1.0,取整数位1,结果为0.01
第三步: 当小数位为0时,就停止计算。
结论:整数二进制加小数二进制,结果为:1011 + 0.01 = 1011.01
备注:此处用小数0.25计算有点取巧,因为小数最后一个尾数如不是5,计算的时候不可能出现小数部分为0的结果,导致只能一直计算到最大要求的位数停止计算。简单说:只是小数位不为0,就可能一直计算下去。
三)二进制转十进制
整数位转换原理:二进制转十进制采用“乘2次方”法。
例如:把二进制1011转十进制步骤如下:
从右到左依次乘以2的次方,次方从0开始,依次累加(2的0次方、2的1次方、2的2次方、2的3次方)。
1011 = 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 8 + 0 + 2 + 1 = 11
结论:1011的十进制为11
小数位转换原理:二进制转十进制采用“乘2负次方”法。
例如:把二进制1011.01转十进制步骤如下:
先计算整数部分,1011的十进制为11
再计算小数部分0.01,依次为乘2的0次方,乘2的-1次方,除2的-2次方。
0.01 = (0 * 2^0) + (0 * 2^-1) + (1 / 2^-2) = 0 + 0 + 0.25 = 0.25
结论:1011.01的十进制为:11+ 0.25 = 11.25
备注:进制的换算只能自己多算算,常用的十进制和二进制转换几乎都是在2到100之间,可以自己全部换算一遍。
四)2的次方表
2的0次方是1(任何数的0次方都是1,0的0次方无意义)
2的1次方是2
2的2次方是4
2的3次方是8
2的4次方是16
2的5次方是32
2的6次方是64
2的7次方是128
2的8次方是256
2的9次方是512
2的10次方是1024
五)进制转换表(2到100)
| 十进制 | 二进制 |
|---|---|
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
| 21 | 10101 |
| 22 | 10110 |
| 23 | 10111 |
| 24 | 11000 |
| 25 | 11001 |
| 26 | 11010 |
| 27 | 11011 |
| 28 | 11100 |
| 29 | 11101 |
| 30 | 11110 |
| 31 | 11111 |
| 32 | 100000 |
| 33 | 100001 |
| 34 | 100010 |
| 35 | 100011 |
| 36 | 100100 |
| 37 | 100101 |
| 38 | 100110 |
| 39 | 100111 |
| 40 | 101000 |
| 41 | 101001 |
| 42 | 101010 |
| 43 | 101011 |
| 44 | 101100 |
| 45 | 101101 |
| 46 | 101110 |
| 47 | 101111 |
| 48 | 110000 |
| 49 | 110001 |
| 50 | 110010 |
| 51 | 110011 |
| 52 | 110100 |
| 53 | 110101 |
| 54 | 110110 |
| 55 | 110111 |
| 56 | 111000 |
| 57 | 111001 |
| 58 | 111010 |
| 59 | 111011 |
| 60 | 111100 |
| 61 | 111101 |
| 62 | 111110 |
| 63 | 111111 |
| 64 | 1000000 |
| 65 | 1000001 |
| 66 | 1000010 |
| 67 | 1000011 |
| 68 | 1000100 |
| 69 | 1000101 |
| 70 | 1000110 |
| 71 | 1000111 |
| 72 | 1001000 |
| 73 | 1001001 |
| 74 | 1001010 |
| 75 | 1001011 |
| 76 | 1001100 |
| 77 | 1001101 |
| 78 | 1001110 |
| 79 | 1001111 |
| 80 | 1010000 |
| 81 | 1010001 |
| 82 | 1010010 |
| 83 | 1010011 |
| 84 | 1010100 |
| 85 | 1010101 |
| 86 | 1010110 |
| 87 | 1010111 |
| 88 | 1011000 |
| 89 | 1011001 |
| 90 | 1011010 |
| 91 | 1011011 |
| 92 | 1011100 |
| 93 | 1011101 |
| 94 | 1011110 |
| 95 | 1011111 |
| 96 | 1100000 |
| 97 | 1100001 |
| 98 | 1100010 |
| 99 | 1100011 |
| 100 | 1100100 |
识别二维码关注个人微信公众号

本章完结,待续,欢迎转载!
本文说明:该文章属于原创,如需转载,请标明文章转载来源!
最后
以上就是柔弱树叶最近收集整理的关于十进制转二进制的全部内容,更多相关十进制转二进制内容请搜索靠谱客的其他文章。








发表评论 取消回复