POJ3070矩阵快速幂

一般矩阵快速幂都和斐波那契数列有关系
废话阶段……
①实质是一种动态规划dp
②需要掌握快速幂的思维
③递推式子如下

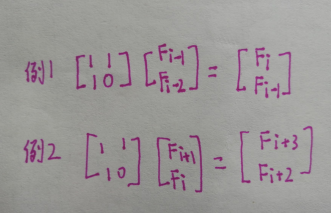
（抱歉字丑）
矩阵快速幂用到了三个小点，一是矩阵乘法，二是快速幂思想（很容易可以get，这里没有讲哦），三是dp的一种思维，每个点都比较容易掌握，掌握了思路之后，再来自己做出来就很容易，自己实现不建议看模板，实现完了，再去对比。

//我写的lowB代码
#include <iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
#define maxn 3005

long long mod=10000;
long long ans[2];
long long cun[2][2];
long long juzhen(int b)
{
    ans[0]=1;
    ans[1]=1;
    long long tmp[2][2]= {{1,1},{1,0}};    

    while(b>0)
    {
        if(b&1)
        {
            int tmp1=tmp[0][0]*ans[0]+tmp[0][1]*ans[1];
            int tmp2=tmp[1][0]*ans[0]+tmp[1][1]*ans[1];
            ans[0]=tmp1%mod;
            ans[1]=tmp2%mod;
        }
        b=b>>1;
        memset(cun,0,sizeof(cun));      //运用一个临时矩阵来存储每位的运算
        for(int i=0; i<2; i++)
        {
            for(int j=0; j<2; j++)
            {
                for(int z=0; z<2; z++)
                {
                    cun[i][j]+=tmp[i][z]*tmp[z][j];
                }
            }
        }
        for(int i=0; i<2; i++)      //放回
        {
            for(int j=0; j<2; j++)
                tmp[i][j]=cun[i][j]%mod;
        }
    }
    return ans[0];
}

int main()
{

    long long x;
    while(cin>>x)
    {
        if(x==0)
        {
            cout<<0<<endl;
            continue;
        }
        if(x==-1)
            break;
        cout<<juzhen(x-2)<<endl;;
    }

    return 0;
}

最后

以上就是着急毛豆为你收集整理的POJ3070矩阵快速幂的全部内容，希望文章能够帮你解决POJ3070矩阵快速幂所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。